गणित के अध्ययन करना चाहिए क्योंकि यह केवल गणित के माध्यम से प्रकृति को समान रूप से समझा जा सकता है। - बर्कहॉफ्फ

8.1 परिचय

ज्यामिति में, हमने विभिन्न ज्यामितीय आकृतियों (त्रिभुज, आयत, ट्रैपेजियम और वृत्त आदि) के क्षेत्रफल की गणना के लिए सूत्र सीखे हैं। ऐसे सूत्र गणित के विभिन्न वास्तविक जीवन समस्याओं में अनुप्रयोग के लिए मूलभूत हैं। प्राथमिक ज्यामिति के सूत्र हमें बहुत सारे सरल आकृतियों के क्षेत्रफल की गणना करने में सक्षम बनाते हैं। हालांकि, वे वक्रों द्वारा घिरे क्षेत्रफल की गणना के लिए पर्याप्त नहीं हैं। इसके लिए हमें समाकलन के कुछ अवधारणाओं की आवश्यकता होगी।

पिछले पाठ में, हमने वक्र $y = f(x)$, अक्ष $x = a$, $x = b$ और $x$-अक्ष द्वारा घिरे क्षेत्र की गणना के लिए समाकलन के रूप में योग के सीमा के रूप में अध्ययन किया था। यहां, इस पाठ में, हम एक विशिष्ट अनुप्रयोग के बारे में अध्ययन करेंगे जिसके माध्यम से हम सरल वक्रों के तल के नीचे क्षेत्रफल, रेखाओं और वृत्त, पराबोला और अतिपरवलय (मानक रूप केवल) के चापों के बीच क्षेत्रफल की गणना कर सकते हैं। हम इन वक्रों द्वारा घिरे क्षेत्रफल की गणना के बारे में भी अध्ययन करेंगे।

एल। सी। कूची (1789-1857)

8.2 सरल वक्रों के तल के नीचे क्षेत्रफल

पिछले पाठ में, हमने समाकलन को एक योग के सीमा के रूप में अध्ययन किया था और गणित के मूल उपप्रमेय के माध्यम से समाकलन की गणना करने के तरीके के बारे में अध्ययन किया था। अब, हम वक्र $y = f(x)$, $x$-अक्ष और अक्ष $x = a$ और $x = b$ द्वारा घिरे क्षेत्र की गणना के लिए आसान और समझदार तरीके के बारे में अध्ययन करेंगे। चित्र 8.1 से, हम वक्र के तल के नीचे क्षेत्र को बहुत सारे बहुत पतले ऊर्ध्वाधर बैंडों से मिलकर बने होने के रूप में सोच सकते हैं। एक असंगत बैंड की ऊंचाई $y$ और चौड़ाई $dx$ हो, तो $dA$ (मूल बैंड के क्षेत्रफल) $= y dx$, जहां $y = f(x)$ है।

इस क्षेत्र को प्राथमिक क्षेत्र कहते हैं जो किसी मान $x$ के बीच $a$ और $b$ के बीच एक अस्थिर स्थिति पर स्थित होता है। हम इस क्षेत्र के कुल क्षेत्र $A$ को $x$-अक्ष, अपवर्तक $x=a, x=b$ और वक्र $y=f(x)$ के बीच के क्षेत्र के रूप में सोच सकते हैं, जो क्षेत्र PQRSP में छोटे बैंड के प्राथमिक क्षेत्रों के जोड़ के रूप में होता है। चिह्नित रूप से, हम इसे व्यक्त करते हैं:

$ \mathrm{A}=\int _{a}^{b} d \mathrm{~A}=\int _{a}^{b} y d x=\int _{a}^{b} f(x) d x $

वक्र $x=g(y), y$-अक्ष और रेखाओं $y=c$, $y=d$ द्वारा सीमित क्षेत्र के क्षेत्र $A$ को निम्नलिखित द्वारा दिया जाता है:

$ \mathrm{A}=\int _{c}^{d} x d y=\int _{c}^{d} g(y) d y $

यहाँ, हम चित्र 8.2 में दिखाए गए तरीके से क्षैतिज बैंड को ध्यान में रखते हैं।

चित्र 8.2

टिप्पणी यदि विचार किए जा रहे वक्र की स्थिति $x$-अक्ष के नीचे हो, तो चूंकि $x=a$ से $x=b$ तक $f(x)<0$ होता है, जैसा कि चित्र 8.3 में दिखाया गया है, वक्र, $x$-अक्ष और अपवर्तक $x=a, x=b$ द्वारा सीमित क्षेत्र नकारात्मक आउटपुट देता है। लेकिन, यहाँ केवल क्षेत्र के संख्यात्मक मान को ध्यान में रखा जाता है। इसलिए, यदि क्षेत्र नकारात्मक हो, तो हम इसके अंतर्गत मान लेते हैं, अर्थात, $\left|\int_a^{b} f(x) d x\right|$।

आमतौर पर, यह हो सकता है कि वक्र के कुछ हिस्सा $x$-अक्ष के ऊपर और कुछ हिस्सा $x$-अक्ष के नीचे हो, जैसा कि चित्र 8.4 में दिखाया गया है। यहाँ, $A_1<0$ और $A_2>0$ है। इसलिए, वक्र $y=f(x), x$-अक्ष और अपवर्तक $x=a$ और $x=b$ द्वारा सीमित क्षेत्र $A$ को $A=|A_1|+A_2$ के रूप में दिया जाता है।

चित्र 8.4

उदाहरण 1 वृत्त $x^{2}+y^{2}=a^{2}$ द्वारा सीमित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

हल चित्र 8.5 से, दिए गए वृत्त द्वारा घिरे क्षेत्र का कुल क्षेत्रफल $=4$ (क्षेत्र $AOBA$ का क्षेत्रफल जो वक्र, $x$-अक्ष और अपवर्तक $x=0$ और $x=a$ द्वारा सीमित है) [क्योंकि वृत्त दोनों $x$-अक्ष और $y$-अक्ष के संदर्भ में सममित है]

$ \begin{aligned} & =4 \int_0^{a} y d x \text{ (ऊर्ध्वाधर बैंड लेकर)} \\ & =4 \int_0^{a} \sqrt{a^{2}-x^{2}} d x \end{aligned} $

$\text{क्योंकि}$ $x^{2}+y^{2}=a^{2}$ द्वारा $\quad y= \pm \sqrt{a^{2}-x^{2}}$

चित्र 8.5

क्षेत्र $AOBA$ पहले चतुर्थांश में है, इसलिए $y$ के धनात्मक मान को लिया जाता है। समाकलन करने पर, हमें दिए गए वृत्त द्वारा घिरे क्षेत्र का कुल क्षेत्रफल प्राप्त होता है

$ \begin{aligned} & =4\left[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{x}{a}\right]_0^{a} \\ & =4\left[\left(\frac{a}{2} \times 0+\dfrac{a^{2}}{2} \sin ^{-1} 1\right)-0\right]=4\left(\dfrac{a^{2}}{2}\right)\left(\dfrac{\pi}{2}\right)=\pi a^{2} \end{aligned} $

$\mathbf{अलग-अलग}$, चित्र 8.6 में दिखाए गए ऊर्ध्वाधर बैंड के संदर्भ में वृत्त द्वारा घिरे क्षेत्र का कुल क्षेत्रफल

$ \begin{aligned} & =4 \int_0^{a} x d y=4 \int_0^{a} \sqrt{a^{2}-y^{2}} d y \qquad\text{(क्यों?)} \\ & =4\left[\frac{y}{2} \sqrt{a^{2}-y^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{y}{a}\right]_0^{a} \\ & =4\left[\left(\frac{a}{2} \times 0+\frac{a^{2}}{2} \sin ^{-1} 1\right)-0\right] \\ & =4 \frac{a^{2}}{2} \frac{\pi}{2}=\pi a^{2} \end{aligned} $

चित्र 8.6

उदाहरण 2 वृत्त $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ द्वारा घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए

हल चित्र 8.7 से, वृत्त द्वारा घिरे क्षेत्र $ABA^{\prime} B^{\prime} A$ का क्षेत्रफल

$=4\left(\begin{matrix} \text{ क्षेत्र } A O B A \text{ का क्षेत्रफल पहले चतुर्थांश में जो वक्र, } x-\text{ अक्ष और अपवर्तक } x=0, x=a \text{ द्वारा सीमित है} \\ \end{matrix} \right)$

$\qquad$ (क्योंकि वृत्त दोनों $x$-अक्ष और $y$-अक्ष के संदर्भ में सममित है)

$=4 \int_0^{a} y d x \quad$ (ऊर्ध्वाधर बैंड लेकर)

$\text{अब }\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ द्वारा $y= \pm \dfrac{b}{a} \sqrt{a^{2}-x^{2}}$ प्राप्त होता है, लेकिन क्षेत्र $AOBA$ प्रथम चतुर्थांश में है, इसलिए $y$ को धनात्मक लिया जाता है। अतः, आवश्यक क्षेत्रफल है

$ \begin{aligned} & =4 \int _{0}^{a} \frac{b}{a} \sqrt{a^{2}-x^{2}} d x \\ & =\frac{4 b}{a}\left[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{x}{a}\right] _{0}^{a} \text { (क्यों?) } \\ & =\frac{4 b}{a}\left[\left(\frac{a}{2} \times 0+\frac{a^{2}}{2} \sin ^{-1} 1\right)-0\right] \\ & =\frac{4 b}{a} \frac{a^{2}}{2} \frac{\pi}{2}=\pi a b \text { } \end{aligned} $

चित्र 8.7

$\text{वैकल्पिक रूप से}$, चित्र 8.8 में दिखाए गए ऊर्ध्वाधर बैंड को ध्यान में रखते हुए वृत्त का क्षेत्रफल है

$ \begin{aligned} & =4 \int_0^{b} x d y=4 \frac{a}{b} \int_0^{b} \sqrt{b^{2}-y^{2}} d y \text{ (क्यों?) } \\ & =\frac{4 a}{b}\left[\frac{y}{2} \sqrt{b^{2}-y^{2}}+\frac{b^{2}}{2} \sin ^{-1} \frac{y}{b}\right]_0^{b} \\ & =\frac{4 a}{b}\left[\left(\frac{b}{2} \times 0+\frac{b^{2}}{2} \sin ^{-1} 1\right)-0\right] \\ & =\frac{4 a}{b} \frac{b^{2}}{2} \frac{\pi}{2}=\pi a b \end{aligned} $

चित्र 8.8

एक्सरसाइज 8.1

1. समीकरण $\frac{x^{2}}{16}+\frac{y^{2}}{9}=1$ द्वारा घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर दिखाएं

हल

दी गई वृत्त के समीकरण, $\frac{x^{2}}{16}+\frac{y^{2}}{9}=1$, को निम्नलिखित रूप में प्रस्तुत किया जा सकता है

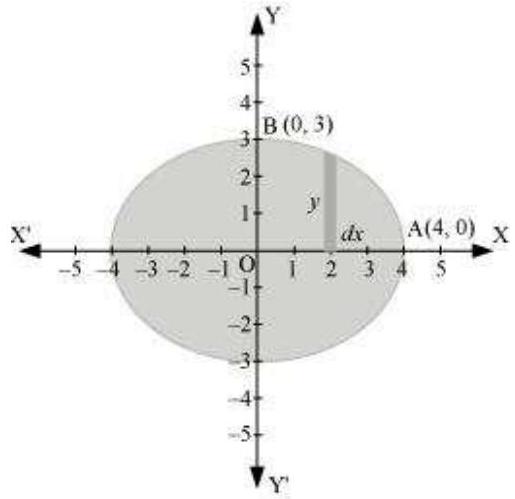
यह देखा जा सकता है कि वृत्त $x$-अक्ष और $y$-अक्ष के संदर्भ में सममित है।

$\therefore$ वृत्त द्वारा घिरे क्षेत्रफल $=4 \times$ OAB क्षेत्रफल

$ \begin{aligned} \text{ OAB क्षेत्रफल } & =\int_0^{4} y d x \\ & =\int_0^{4} 3 \sqrt{1-\frac{x^{2}}{16}} d x \\ & =\frac{3}{4} \int_0^{4} \sqrt{16-x^{2}} d x \\ & =\frac{3}{4}[\frac{x}{2} \sqrt{16-x^{2}}+\frac{16}{2} \sin ^{-1} \frac{x}{4}]_0^{4} \\ & =\frac{3}{4}[2 \sqrt{16-16}+8 \sin ^{-1}(1)-0-8 \sin ^{-1}(0)] \\ & =\frac{3}{4}[\frac{8 \pi}{2}] \\ & =\frac{3}{4}[4 \pi] \\ & =3 \pi \end{aligned} $

इसलिए, वृत्त द्वारा घिरे क्षेत्रफल $=4 \times 3\pi =12 \pi$ इकाई

2. समीकरण $\frac{x^{2}}{4}+\frac{y^{2}}{9}=1$ द्वारा घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर दिखाएं

हल

दी गई वृत्त के समीकरण को निम्नलिखित रूप में प्रस्तुत किया जा सकता है

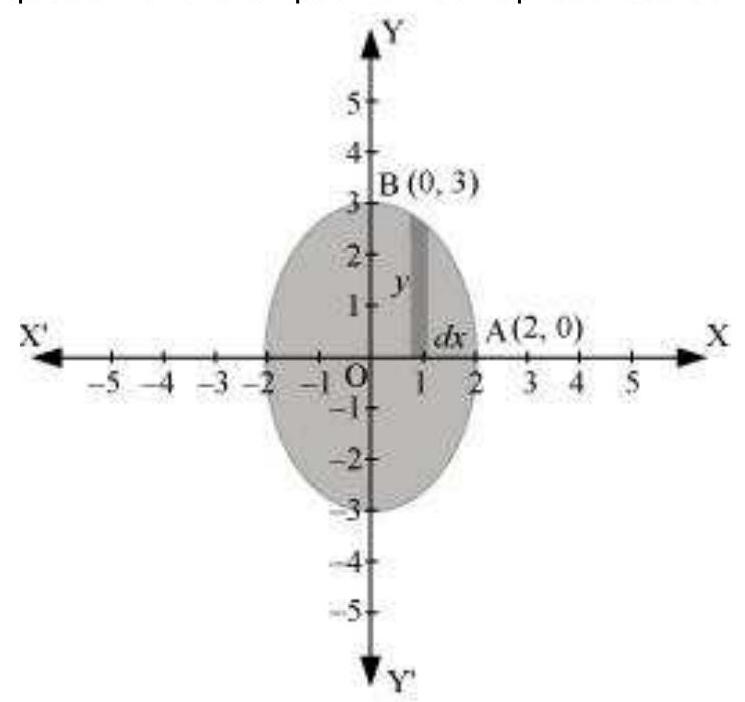
$\frac{x^{2}}{4}+\frac{y^{2}}{9}=1$

$\Rightarrow y=3 \sqrt{1-\frac{x^{2}}{4}}$

यह देखा जा सकता है कि वृत्त $x$-अक्ष और $y$-अक्ष के संदर्भ में सममित है।

$\therefore$ वृत्त द्वारा घिरे क्षेत्रफल $=4 \times$ OAB क्षेत्रफल $\therefore$ OAB क्षेत्रफल $=\int_0^{2} y d x$

$ \begin{aligned} & =\int_0^{2} 3 \sqrt{1-\frac{x^{2}}{4}} d x \quad \text{ [समीकरण (1) का उपयोग करके] } \\ & =\frac{3}{2} \int_0^{2} \sqrt{4-x^{2}} d x \\ & =\frac{3}{2}[\frac{x}{2} \sqrt{4-x^{2}}+\frac{4}{2} \sin ^{-} \frac{x}{2}]_0^{2} \\ & =\frac{3}{2}[\frac{2 \pi}{2}] \\ & =\frac{3 \pi}{2} \end{aligned} $

इसलिए, वृत्त द्वारा घिरे क्षेत्र का क्षेत्रफल $=4 \times \frac{3 \pi}{2}=6 \pi$ इकाई है

निम्नलिखित अभ्यास 3 और 4 में सही उत्तर का चयन करें।

3. पहले चतुर्थांश में वृत्त $x^{2}+y^{2}=4$ और रेखाओं $x=0$ और $x=2$ द्वारा घिरे क्षेत्र का क्षेत्रफल है

$\quad\quad$(A) $\pi$

$\quad\quad$(B) $\frac{\pi}{2}$

$\quad\quad$(C) $\frac{\pi}{3}$

$\quad\quad$(D) $\frac{\pi}{4}$

उत्तर दिखाएं

हल

वृत्त और रेखाओं $x=0$ और $x=2$ द्वारा पहले चतुर्थांश में घिरे क्षेत्र को निम्नलिखित चित्र द्वारा प्रस्तुत किया गया है

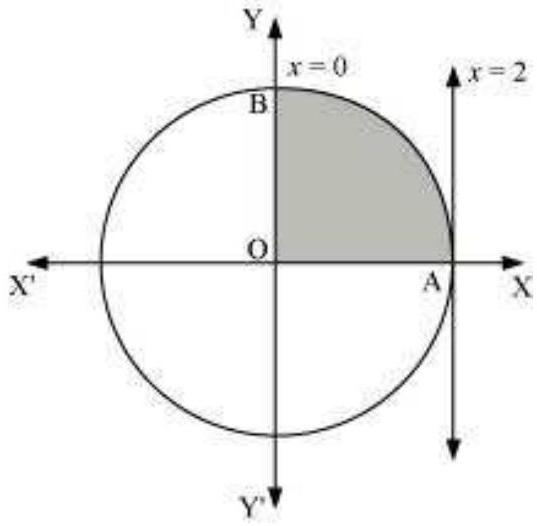
$ \begin{aligned} \therefore \text{ क्षेत्र OAB } & =\int_0^{2} y d x \\ & =\int_0^{2} \sqrt{4-x^{2}} d x \\ & =[\frac{x}{2} \sqrt{4-x^{2}}+\frac{4}{2} \sin ^{-1} \frac{x}{2}]_0^{2} \\ & =2(\frac{\pi}{2}) \\ & =\pi \text{ इकाई } \end{aligned} $

इसलिए, सही उत्तर $A$ है।

4. वक्र $y^{2}=4 x$, $y$-अक्ष और रेखा $y=3$ द्वारा घिरे क्षेत्र का क्षेत्रफल है

$\quad\quad$(A) 2

$\quad\quad$(B) $\frac{9}{4}$

$\quad\quad$(C) $\frac{9}{3}$

$\quad\quad$(D) $\frac{9}{2}$

उत्तर दिखाएं

हल

वक्र, $y^{2}=4 x$, $y$-अक्ष और $y=3$ द्वारा घिरे क्षेत्र को निम्नलिखित चित्र द्वारा प्रस्तुत किया गया है

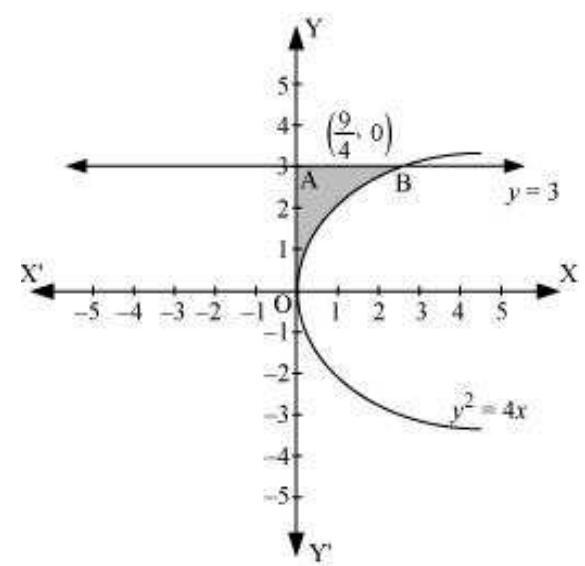
$\therefore$ क्षेत्रफल $OAB=\int_0^{3} x d y$

$ =\int_0^{3} \frac{y^{2}}{4} d y $

$ \begin{aligned} & =\frac{1}{4}[\frac{y^{3}}{3}]_0^{3} \\ & =\frac{1}{12}(27) \\ & =\frac{9}{4} \text{ units } \end{aligned} $

इसलिए, सही उत्तर $B$ है।

विविध उदाहरण

उदाहरण 3 रेखा $y=3 x+2$, $x$-अक्ष और अपवर्तक $x=-1$ और $x=1$ द्वारा घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

हल चित्र 8.9 में दिखाए गए अनुसार, रेखा $y=3 x+2$ $x$-अक्ष को $x=\dfrac{-2}{3}$ पर मिलती है और इसका ग्राफ $x \in \left(-1, \dfrac{-2}{3}\right)$ के लिए $x$-अक्ष के नीचे और $x \in \left(\dfrac{-2}{3}, 1\right)$ के लिए $x$-अक्ष के ऊपर रहता है।

आवश्यक क्षेत्र $=$ क्षेत्र $ACBA$ का क्षेत्रफल $+$ क्षेत्र $ADEA$ का क्षेत्रफल

$ \begin{aligned} & =\left|\int _{-1}^{\frac{-2}{3}}(3 x+2) d x\right|+\int _{\frac{-2}{3}}^{1}(3 x+2) d x \\ & =\left|\left[\dfrac{3 x^{2}}{2}+2 x\right] _{-1}^{\frac{-2}{3}}\right|+\left[\dfrac{3 x^{2}}{2}+2 x\right] _{\frac{-2}{3}}^{1}=\dfrac{1}{6}+\dfrac{25}{6}=\dfrac{13}{3} \end{aligned} $

चित्र 8.9

उदाहरण 4 वक्र $y=\cos x$ के द्वारा $x=0$ और $x=2 \pi$ के बीच घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

हल चित्र 8.10 से, आवश्यक क्षेत्र $=$ क्षेत्र $OABO$ का क्षेत्रफल $+$ क्षेत्र $BCDB$ का क्षेत्रफल $+$ क्षेत्र $DEFD$ का क्षेत्रफल।

इसलिए, हमें आवश्यक क्षेत्र

$ \begin{aligned} & =\int_ 0^{\frac{\pi}{2}} \cos x d x+\left|\int_ {\frac{\pi}{2}}^{\frac{3 \pi}{2}} \cos x d x\right|+\int_ {\frac{3 \pi}{2}}^{2 \pi} \cos x d x \\ & =[\sin x]_ 0^{\frac{\pi}{2}}+\left|[\sin x]_ {\frac{\pi}{2}}^{\frac{3 \pi}{2}}\right|+[\sin x]_ {\frac{3 \pi}{2}}^{2 \pi} \\ & =1+2+1=4 \end{aligned} $

अध्याय 8 पर समान अभ्यास प्रश्न

1. दिए गए वक्रों और रेखाओं के तल के नीचे क्षेत्रफल ज्ञात कीजिए:

$\quad\quad$(i) $y=x^{2}, x=1, x=2$ और $x$-अक्ष

$\quad\quad$(ii) $y=x^{4}, x=1, x=5$ और $x$-अक्ष

उत्तर दिखाएं

हल

i. आवश्यक क्षेत्रफल द्वारा छायांकित क्षेत्र ADCBA को प्रस्तुत करता है

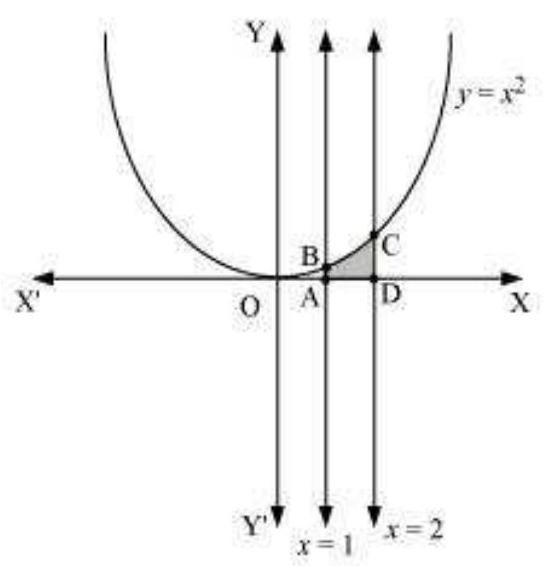
$ \begin{aligned} \text{ क्षेत्रफल ADCBA } & =\int_1^{2} y d x \\ & =\int_1^{2} x^{2} d x \\ & =[\frac{x^{3}}{3}]_1^{2} \\ & =\frac{8}{3}-\frac{1}{3} \\ & =\frac{7}{3} \text{ इकाई } \end{aligned} $

ii. आवश्यक क्षेत्रफल द्वारा छायांकित क्षेत्र ADCBA को प्रस्तुत करता है

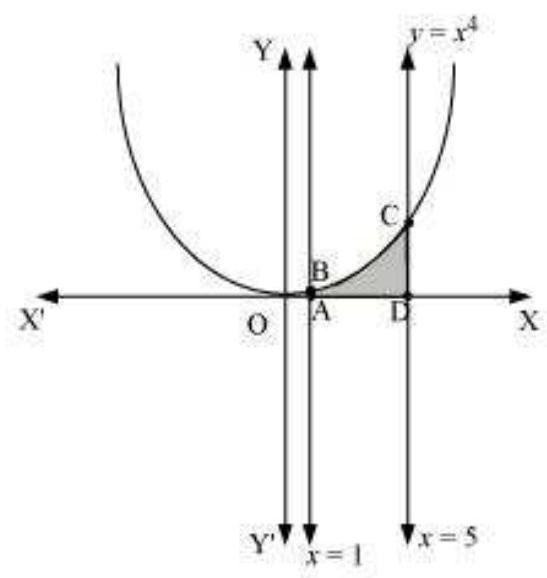
$ \begin{aligned} \text{ क्षेत्रफल ADCBA } & =\int_1^{5} x^{4} d x \\ & =[\frac{x^{5}}{5}]_1^{5} \\ & =\frac{(5)^{5}}{5}-\frac{1}{5} \\ & =(5)^{4}-\frac{1}{5} \\ & =625-\frac{1}{5} \\ & =624.8 \text{ इकाई } \end{aligned} $

2. $y=|x+3|$ के ग्राफ को बनाएं और $\int _{-6}^{0}|x+3| d x$ का मूल्यांकन करें।

उत्तर दिखाएं

हल

दिया गया समीकरण $y=|x+3|$ है

$x$ और $y$ के संगत मान निम्नलिखित तालिका में दिए गए हैं।

$x$	-6	-5	-4	-3	-2	-1	0
$y$	3	2	1	0	1	2	3

इन बिंदुओं को आलेखित करने पर, हमें $y=|x+3|$ के ग्राफ के निम्नलिखित रूप मिलता है।

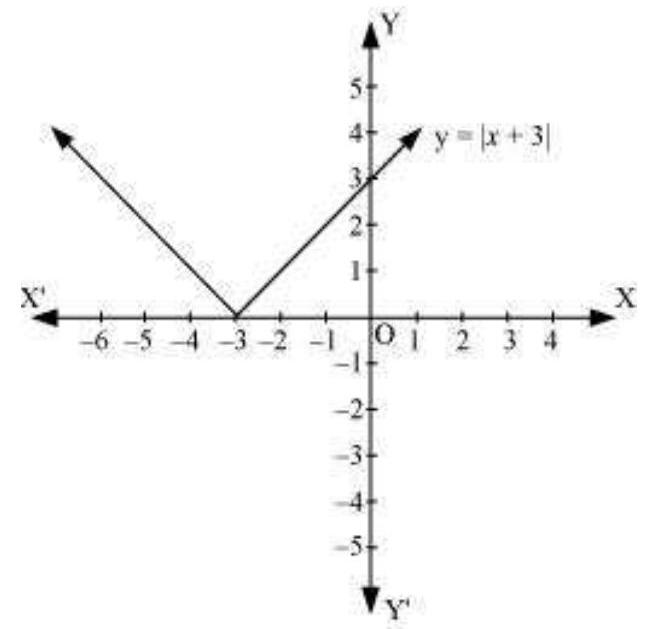
ज्ञात है कि, $(x+3) \leq 0$ जब $-6 \leq x \leq-3$ और $(x+3) \geq 0$ जब $-3 \leq x \leq 0$

$ \begin{aligned} \therefore \int _{-6}^{0}|(x+3)| d x & =-\int _{-6}^{-3}(x+3) d x+\int _{-3}^{0}(x+3) d x \\ & =-[\frac{x^{2}}{2}+3 x] _{-6}^{-3}+[\frac{x^{2}}{2}+3 x] _{-3}^{0} \\ & =-[(\frac{(-3)^{2}}{2}+3(-3))-(\frac{(-6)^{2}}{2}+3(-6))]+[0-(\frac{(-3)^{2}}{2}+3(-3)]] \\ & =-[-\frac{9}{2}]-[-\frac{9}{2}] \\ & =9 \end{aligned} $

3. वक्र $y=\sin x$ के द्वारा $x=0$ और $x=2 \pi$ के बीच घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

उत्तर दिखाएं

हल

$y=\sin x$ के ग्राफ को खींचा जा सकता है

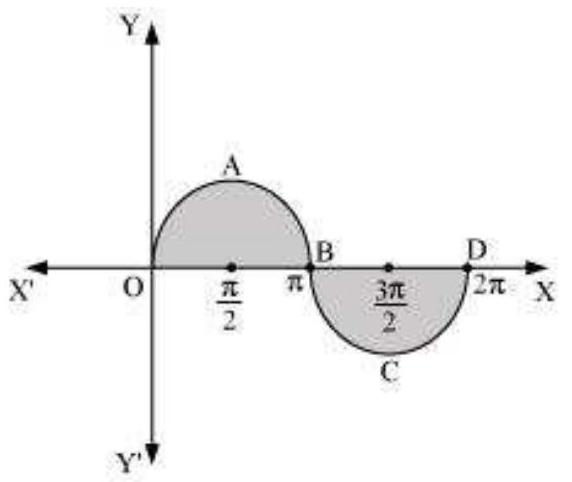
$\therefore$ आवश्यक क्षेत्रफल $=$ क्षेत्र $OABO+$ क्षेत्र $BCDB$

$ \begin{aligned} & =\int_0^{\pi} \sin x d x+|\int _{\pi}^{2 \pi} \sin x d x| \\ & =[-\cos x]_0^{\pi}+|[-\cos x] _{\pi}^{2 \pi}| \\ & =[-\cos \pi+\cos 0]+|-\cos 2 \pi+\cos \pi| \\ & =1+1+|(-1-1)| \\ & =2+|-2| \\ & =2+2=4 \text{ इकाई } \end{aligned} $

निम्नलिखित प्रश्न 4 से 5 तक दिए गए अभ्यास में सही उत्तर का चयन कीजिए।

4. वक्र $y=x^{3}$, x-अक्ष और अपवर्तक $x=-2$ और $x=1$ द्वारा घिरे क्षेत्र का क्षेत्रफल है

$\quad\quad$(A) -9

$\quad\quad$(B) $\frac{-15}{4}$

$\quad\quad$(C) $\frac{15}{4}$

$\quad\quad$(D) $\frac{17}{4}$

उत्तर दिखाएं

हल

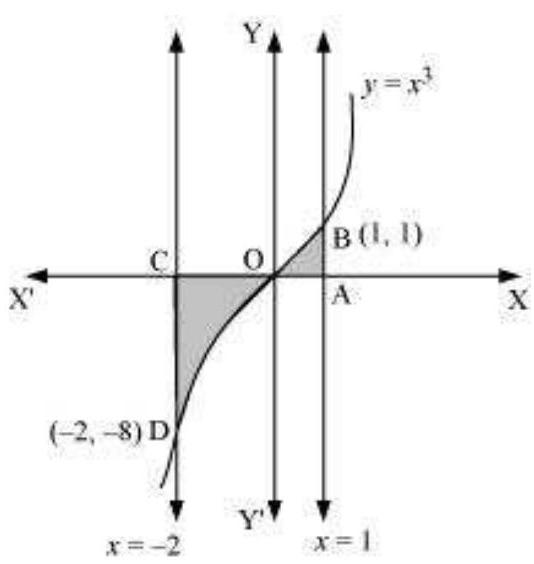
आवश्यक क्षेत्रफल $=\int _{-2}^{1} y d x$

1 धनात्मक और ऋणात्मक क्षेत्र की पहचान करें:

• हम जानते हैं कि वक्र x = -2 और x = 0 के बीच x-अक्ष के नीचे गिर जाता है (लगभग x = -1 के बिंदु पर)।

• इसलिए, हम वक्र के तल के नीचे क्षेत्रफल की गणना दो खंडों में करेंगे:

  • x-अक्ष के ऊपर क्षेत्रफल: x = 0 से x = 1 तक (धनात्मक)
  • x-अक्ष के नीचे क्षेत्रफल: x = -2 से x = 0 तक (ऋणात्मक)

2 सीमित समाकलन बनाएं:

• x-अक्ष के ऊपर क्षेत्रफल: ∫₀¹ (x^3) dx
• x-अक्ष के नीचे क्ष त्रफल: ∫-20 (x^3) dx (यहां ऋणात्मक चिह्न का ध्यान रखें ताकि x-अक्ष के नीचे क्षेत्रफल को गिना जा सके)

3 समाकलन का मूल्यांकन करें: पिछले चरण के जैसे ही शक्ति नियम का उपयोग करते हुए:

• x-अक्ष के ऊपर क्षेत्रफल: [(x^4)/4]₀¹ = (1/4)
• x-अक्ष के नीचे क्षेत्रफल: |[(-x^4)/4]₋²⁰| = (16/4) (धनात्मक क्षेत्रफल को गिनने के लिए अंतर्गत धनात्मक मान लें)

4 समाप्त घिरे क्षेत्रफल की गणना करें:

• समाप्त घिरे क्षेत्रफल = x-अक्ष के ऊपर क्षेत्रफल + x-अक्ष के नीचे क्षेत्रफल = (1/4) + (16/4) = 17/4

सही विकल्प D है।

5. वक्र $y=x|x|, x$-अक्ष और अपवर्तक $x=-1$ और $x=1$ द्वारा घिरे क्षेत्रफल को निम्न द्वारा दिया गया है

$\quad\quad$(A) 0

$\quad\quad$(B) $\frac{1}{3}$

$\quad\quad$(C) $\frac{2}{3}$

$\quad\quad$(D) $\frac{4}{3}$

[संकेत : $y=x^{2}$ यदि $x>0$ और $y=-x^{2}$ यदि $.x<0$].

सारांश

• वक्र $y=f(x), x$-अक्ष और रेखाओं $x=a$ और $x=b(b>a)$ द्वारा सीमित क्षेत्र का क्षेत्रफल निम्न फॉर्मूला द्वारा दिया जाता है: क्षेत्रफल $=\int_a^{b} y d x=\int_a^{b} f(x) d x$।

• वक्र $x=\phi(y), y$-अक्ष और रेखाओं $y=c, y=d$ द्वारा सीमित क्षेत्र का क्षेत्रफल निम्न फॉर्मूला द्वारा दिया जाता है: क्षेत्रफल $=\int_c^{d} x d y=\int_c^{d} \phi(y) d y$।

ऐतिहासिक टिप्पणी

समाकलन कलन के उत्पति गणित के विकास के जल्दी अवधि में वापस जाती है और यह प्राचीन ग्रीक गणितज्ञों द्वारा विकसित किए गए विधि के अंतर्गत आती है। यह विधि तल आकृतियों के क्षेत्रफल, सतह क्षेत्रफल और ठोस वस्तुओं के आयतन आदि की गणना के समस्याओं के हल के लिए उत्पन्न हुई। इस अर्थ में, विधि के अंतर्गत विधि के अंतर्गत एक प्रारंभिक विधि के रूप में देखा जा सकता है।

of integration. जल्दी के अवधि में विधि के सबसे बड़े विकास का प्राप्त करना एडोक्सस (440 ई.पू.) और आर्किमिडीज (300 ई.पू.) के कार्यों में हुआ था।

कलकुलस के सिद्धांत के नियमित अनुपात की शुरुआत 17 वीं शताब्दी में हुई। 1665 में न्यूटन ने कलकुलस के अपने कार्य पर शुरू किया जिसे उन्होंने फ्लक्सियन के सिद्धांत के रूप में वर्णित किया था और वे अपने सिद्धांत का उपयोग एक वक्र पर किसी बिंदु पर स्पर्श रेखा और वक्रता त्रिज्या के खोजने में किया। न्यूटन ने व्युत्क्रम फलन के मूल अवधारणा को व्युत्क्रम विधि (अनिश्चित समाकलन) या स्पर्श विधि के रूप में परिचय दिया।

1684-86 के बीच, लेब्निज ने एक्टा एरुडोरम में एक लेख प्रकाशित किया जिसे उन्होंने कैल्कुलस सम्मार्त्तुस कहा क्योंकि यह अनेक अपरिमित छोटे क्षेत्रों के योग के संबंध में था, जिसके योग को उन्होंने ’ ’ ’ चिह्न द्वारा इंगित किया। 1696 में, वे जे. बर्नूली द्वारा दिए गए सुझाव का पालन करते हुए इस लेख को कैल्कुलस इंटीग्रली में बदल दिया। यह न्यूटन के स्पर्श विधि के व्युत्क्रम विधि के संगत था।

न्यूटन और लेब्निज ने बहुत स्वतंत्र रूप से अपने अनुपात के रास्ते को अपनाया जो बुनियादी रूप से अलग थे। हालांकि, अपने सिद्धांतों द्वारा प्राप्त किए गए परिणाम व्यावहारिक रूप से समान थे। लेब्निज ने निश्चित समाकलन के अवधारणा का उपयोग किया और यह बिलकुल स्पष्ट है कि वे पहले ही व्युत्क्रम फलन और निश्चित समाकलन के बीच संबंध को स्पष्ट रूप से समझे थे।

संक्षिप्त रूप से, कलन के मूल अवधारणा और सिद्धांत और विशेष रूप से इसके अवकलन कलन से संबंध अंतिम 17 वीं शताब्दी में पी. डी. फर्मेट, आई. न्यूटन और जी. लेब्निज के कार्यों में विकसित हुए थे। हालांकि, इसकी व्याख्या सीमा के अवधारणा के आधार पर केवल 19 वीं शताब्दी के प्रारंभ में एल. कॉशी के कार्यों में हुई। अंत में, लियो शॉपी के निम्नलिखित उद्धरण का उल्लेख करना महत्वपूर्ण है:

“यह कहा जा सकता है कि अवकल भाग और समाकल के अवधारणा जो अपने मूल रूप से आर्किमिडीज तक जाते हैं, विज्ञान में खोज के अध्ययन द्वारा प्रस्तुत किए गए थे जैसे कि केपलर, डेसकार्ट्स, कैवलियरी, फर्मेट और वॉलिस … अवकलन और समाकलन के व्युत्क्रम कार्यों की खोज न्यूटन और लेब्निज के पास है।”