हल

एक वृत्त के क्षेत्रफल ( $A$ ) के त्रिज्या $(r)$ के द्वारा दिया गया है,

$A=\pi r^{2}$

अब, क्षेत्रफल के परिवर्तन दर को उसकी त्रिज्या के संदर्भ में दिया गया है,

$\frac{d A}{d r}=\frac{d}{d r}(\pi r^{2})=2 \pi r$

1. जब $r=3 सेमी$,

$\frac{d A}{d r}=2 \pi(3)=6 \pi$

अतः, जब वृत्त की त्रिज्या $3 सेमी$ है, तो उसके क्षेत्रफल के परिवर्तन दर $6 सेमी^{2}/सेकंड$ है।

2. जब $r=4 सेमी$,

$\frac{d A}{d r}=2 \pi(4)=8 \pi$

अतः, जब वृत्त की त्रिज्या $4 सेमी$ है, तो उसके क्षेत्रफल के परिवर्तन दर $8 सेमी^{2}/सेकंड$ है।

हल

मान लीजिए $x$ एक किनारे की लंबाई है, $V$ आयतन है और $s$ सतह क्षेत्रफल है।

तब, $V=x^{3}$ और $S=6 x^{2}$ जहाँ $x$ समय $t$ के फ़ंक्शन है।

दिया गया है कि $\frac{d V}{d t}=8 सेमी^{3}/सेकंड$।

अब, चेन नियम का उपयोग करते हुए, हम निम्नलिखित प्राप्त करते हैं:

$ \therefore=\frac{d V}{d t}=\frac{d}{d t}(x^{3})=\frac{d}{d x}(x^{3}) \cdot \frac{d x}{d t}=3 x^{2} \cdot \frac{d x}{d t} $

$ \begin{equation*} \Rightarrow \frac{d x}{d t}=\frac{8}{3 x^{2}} \tag{1} \end{equation*} $

$ \begin{aligned} & \text{ अब, } \frac{d S}{d t}=\frac{d}{d t}(6 x^{2})=\frac{d}{d x}(6 x^{2}) \cdot \frac{d x}{d t} \quad \text{ [चेन नियम द्वारा] } \\ & =12 x \cdot \frac{d x}{d t}=12 x \cdot(\frac{8}{3 x^{2}})=\frac{32}{x} \end{aligned} $

अतः, यदि घन के किनारे की लंबाई $12 सेमी$ है, तो सतह क्षेत्रफल की दर $\frac{8}{3} सेमी^{2}/सेकंड$ है।

हल

एक वृत्त के क्षेत्रफल $(A)$ की त्रिज्या $(r)$ के साथ दिया गया है,

$A=\pi r^{2}$

अब, क्षेत्रफल $(A)$ के समय $(t)$ के सापेक्ष परिवर्तन द्वारा दिया गया है,

$\frac{d A}{d t}=\frac{d}{d t}(\pi r^{2}) \cdot \frac{d r}{d t}=2 \pi r \frac{d r}{d t} \quad$ [चैन नियम द्वारा]

दिया गया है कि,

$\frac{d r}{d t}=3 cm / s$ $\therefore \frac{d A}{d t}=2 \pi r(3)=6 \pi r$

इसलिए, जब $r=10 cm$,

$\frac{d A}{d t}=6 \pi(10)=60 \pi cm^{2} / s$

अतः, जब त्रिज्या $10 cm$ है, तो वृत्त के क्षेत्रफल की वृद्धि दर $60 \pi cm^{2} / s$ है।

हल

मान लीजिए $x$ एक भुजा की लंबाई और $V$ घन का आयतन है। तब,

$V=x^{3}$.

$\therefore \frac{d V}{d t}=3 x^{2} \cdot \frac{d x}{d t}$ (चैन नियम द्वारा)

दिया गया है कि,

$\frac{d x}{d t}=3 cm / s$

$\therefore \frac{d V}{d t}=3 x^{2}(3)=9 x^{2}$

इसलिए, जब $x=10 cm$,

$\frac{d V}{d t}=9(10)^{2}=900 cm^{3} / s$

अतः, जब किनारा $10 cm$ लंबा हो, तो घन के आयतन की वृद्धि दर $900 cm^{3} / s$ है।

हल

एक वृत्त के क्षेत्रफल $(A)$ की त्रिज्या $(r)$ के साथ दिया गया है $A=\pi r^{2}$.

इसलिए, क्षेत्रफल $(A)$ के समय $(t)$ के सापेक्ष परिवर्तन द्वारा दिया गया है,

$\frac{d A}{d t}=\frac{d}{d t}(\pi r^{2})=\frac{d}{d r}(\pi r^{2}) \frac{d r}{d t}=2 \pi r \frac{d r}{d t}$ [चैन नियम द्वारा]

दिया गया है कि $\frac{d r}{d t}=5 cm / s$.

इसलिए, जब $r=8 cm$,

$\frac{d A}{d t}=2 \pi(8)(5)=80 \pi$

अतः, जब वृत्ताकार तरंग की त्रिज्या $8 cm$ हो, तो घिरे क्षेत्र की वृद्धि दर $80 \pi cm^{2} / s$ है।

हल

एक वृत्त की परिधि $(C)$ त्रिज्या $(r)$ के द्वारा दी गई है $C=2 \pi r$।

इसलिए, समय $(t)$ के सापेक्ष परिधि (C) के परिवर्तन दर को दिया गया है, $\frac{d C}{d t}=\frac{d C}{d r} \cdot \frac{d r}{d t}$ (चैन नियम द्वारा) $=\frac{d}{d r}(2 \pi r) \frac{d r}{d t}$

$=2 \pi \cdot \frac{d r}{d t}$

दिया गया है कि $\frac{d r}{d t}=0.7 , cm / s$।

इसलिए, परिधि की वृद्धि दर $2 \pi(0.7)=1.4 \pi , cm / s$ है।

हल

क्योंकि लंबाई $(x)$ $5 , cm /$ मिनट की दर से घट रही है और चौड़ाई $(y)$ $4 , cm /$ मिनट की दर से बढ़ रही है, हम निम्नलिखित रखते हैं:

$\frac{d x}{d t}=-5 , cm / min$ और $\frac{d y}{d t}=4 , cm / min$

(a) आयत की परिधि $(P)$ निम्नलिखित द्वारा दी गई है,

$P=2(x+y)$

$\therefore \frac{d P}{d t}=2(\frac{d x}{d t}+\frac{d y}{d t})=2(-5+4)=-2 , cm / min$

इसलिए, परिधि $2 , cm / min$ की दर से घट रही है।

(b) आयत के क्षेत्रफल (A) निम्नलिखित द्वारा दिया गया है,

$A=x \times y$

$\therefore \frac{d A}{d t}=\frac{d x}{d t} \cdot y+x \cdot \frac{d y}{d t}=-5 y+4 x$

जब $x=8 , cm$ और $y=6 , cm$, $\frac{d A}{d t}=(-5 \times 6+4 \times 8) , cm^{2} / min=2 , cm^{2} / min$

इसलिए, आयत के क्षेत्रफल $2 , cm^{2} / min$ की दर से बढ़ रहा है।

हल

एक गोले का आयतन $(V)$ त्रिज्या $(r)$ के द्वारा दिया गया है,

$$ V = \frac{4}{3} \pi r^3 $$

इसलिए, आयतन के परिवर्तन दर को निम्नलिखित द्वारा दिया गया है:

$$ \frac{dV}{dt} = 4 \pi r^2 \cdot \frac{dr}{dt} $$

दिया गया है कि $\frac{dV}{dt} = 900 , cm^3/s$ और $r = 15 , cm$।

$$ 900 = 4 \pi (15)^2 \cdot \frac{dr}{dt} $$

$$ 900 = 4 \pi \cdot 225 \cdot \frac{dr}{dt} $$

$$ 900 = 900 \pi \cdot \frac{dr}{dt} $$

$$ \frac{dr}{dt} = \frac{900}{900 \pi} = \frac{1}{\pi} , cm/s $$

इसलिए, गुब्बारे की त्रिज्या के बढ़ने की दर $\frac{1}{\pi} , cm/s$ है।

$V=\frac{4}{3} \pi r^{3}$

$\therefore$ समय $(t)$ के सापेक्ष आयतन $(V)$ के परिवर्तन की दर निम्नलिखित द्वारा दी गई है,

$\frac{d V}{d t}=\frac{d V}{d r} \cdot \frac{d r}{d t} _{\text{[By chain rule] }}$

$=\frac{d}{d r}(\frac{4}{3} \pi r^{3}) \cdot \frac{d r}{d t}$

$=4 \pi r^{2} \cdot \frac{d r}{d t}$

दिया गया है कि $\frac{d V}{d t}=900 cm^{3} / s$.

$\therefore 900=4 \pi r^{2} \cdot \frac{d r}{d t}$

$\Rightarrow \frac{d r}{d t}=\frac{900}{4 \pi r^{2}}=\frac{225}{\pi r^{2}}$

इसलिए, जब त्रिज्या $=15 cm$ है,

$\frac{d r}{d t}=\frac{225}{\pi(15)^{2}}=\frac{1}{\pi}$

अतः, जब त्रिज्या $15 cm$ है, तो बल्ले की त्रिज्या के बढ़ने की दर

$1 cm / s$ है।

इसके बराबर है $\pi$

Solution

एक गोले का आयतन $(V)$ जिसकी त्रिज्या $(r)$ है, निम्नलिखित द्वारा दिया गया है $V=\frac{4}{3} \pi r^{3}$.

आयतन $(V)$ के अपनी त्रिज्या $(r)$ के सापेक्ष परिवर्तन की दर निम्नलिखित द्वारा दी गई है,

$\frac{d V}{d r}=\frac{d}{d r}(\frac{4}{3} \pi r^{3})=\frac{4}{3} \pi(3 r^{2})=4 \pi r^{2}$

इसलिए, जब त्रिज्या $=10 cm$ है,

$\frac{d V}{d r}=4 \pi(10)^{2}=400 \pi$

अतः, बल्ले का आयतन $400 cm^{3} / s$ की दर से बढ़ रहा है।

Solution

मान लीजिए $y$ मीटर दीवार की ऊंचाई जहां चढ़ाई दरां छूती है। अतः, चढ़ाई दरां के नीचे भूमि पर $x$ मीटर दूर होती है।

तब, पाइथागोरस प्रमेय के अनुसार, हमें निम्नलिखित प्राप्त होता है:

$x^{2}+y^{2}=25$ [चढ़ाई दरां की लंबाई $=5 m$ ]

$\Rightarrow y=\sqrt{25-x^{2}}$

तब, ऊंचाई $(y)$ के समय $(t)$ के सापेक्ष परिवर्तन की दर निम्नलिखित द्वारा दी गई है,

$\frac{d y}{d t}=\frac{-x}{\sqrt{25-x^{2}}} \cdot \frac{d x}{d t}$

दिया गया है कि $\frac{d x}{d t}=2\ cm / s$. $\therefore \frac{d y}{d t}=\frac{-2 x}{\sqrt{25-x^{2}}}$

अब, जब $x=4\ m$, तो हमें प्राप्त होता है:

$\frac{d y}{d t}=\frac{-2 \times 4}{\sqrt{25-4^{2}}}=-\frac{8}{3}$

अतः, दीवार पर लदाख की ऊंचाई $\frac{8}{3}\ cm / s$ की दर से घट रही है।

हल

वक्र का समीकरण निम्नलिखित है:

$6 y=x^{3}+2$

कण के स्थिति के संबंध में समय $(t)$ के संबंध में दर निम्नलिखित है,

$6 \frac{d y}{d t}=3 x^{2} \frac{d x}{d t}+0$

$\Rightarrow 2 \frac{d y}{d t}=x^{2} \frac{d x}{d t}$

जब कण के $y$-निर्देशांक $x$-निर्देशांक के 8 गुना तेजी से बदल रहा है अर्थात, $(\frac{d y}{d t}=8 \frac{d x}{d t})$, तो हमें प्राप्त होता है:

$2(8 \frac{d x}{d t})=x^{2} \frac{d x}{d t}$

$\Rightarrow 16 \frac{d x}{d t}=x^{2} \frac{d x}{d t}$

$\Rightarrow(x^{2}-16) \frac{d x}{d t}=0$

$\Rightarrow x^{2}=16$

$\Rightarrow x= \pm 4$

जब $x=4, y=\frac{4^{3}+2}{6}=\frac{66}{6}=11$.

जब $x=-4, y=\frac{(-4)^{3}+2}{6}=-\frac{62}{6}=-\frac{31}{3}$.

अतः, वक्र पर आवश्यक बिंदु $(4,11)$ और $(-4, \frac{-31}{3})$ हैं।

हल

हवा के बुलबुले एक गोले के आकार में है।

अब, एक हवा के बुलबुले $(V)$ के आयतन के लिए त्रिज्या $(r)$ के साथ संबंध निम्नलिखित है,

$V=\frac{4}{3} \pi r^{3}$

आयतन $(V)$ के संबंध में समय $(t)$ के संबंध में दर निम्नलिखित है,

$ \begin{matrix} \frac{d V}{d t} & =\frac{4}{3} \pi \frac{d}{d r}(r^{3}) \cdot \frac{d r}{d t} & \text{ [By chain rule] } \\ & =\frac{4}{3} \pi(3 r^{2}) \frac{d r}{d t} & \\ & =4 \pi r^{2} \frac{d r}{d t} & \end{matrix} $

दिया गया है कि $\frac{d r}{d t}=\frac{1}{2}\ cm / s$।

इसलिए, जब $r=1 cm$,

$\frac{d V}{d t}=4 \pi(1)^{2}(\frac{1}{2})=2 \pi cm^{3} / s$

इसलिए, बुलबुले के आयतन के बढ़ने की दर $2 \pi cm^{3} / s$ है।

हल

एक गोले के आयतन $(V)$ त्रिज्या $(r)$ के साथ दिया गया है,

$V=\frac{4}{3} \pi r^{3}$

यह दिया गया है कि:

व्यास $=\frac{3}{2}(2 x+1)$

$\Rightarrow r=\frac{3}{4}(2 x+1)$

$\therefore V=\frac{4}{3} \pi(\frac{3}{4})^{3}(2 x+1)^{3}=\frac{9}{16} \pi(2 x+1)^{3}$

इसलिए, $x$ के संदर्भ में आयतन के बदले आने की दर निम्नलिखित है

$ \frac{d V}{d x}=\frac{9}{16} \pi \frac{d}{d x}(2 x+1)^{3}=\frac{9}{16} \pi \times 3(2 x+1)^{2} \times 2=\frac{27}{8} \pi(2 x+1)^{2} . $

हल

एक शंकु के आयतन $(V)$ त्रिज्या $(r)$ और ऊंचाई $(h)$ के साथ दिया गया है,

$V=\frac{1}{3} \pi r^{2} h$

यह दिया गया है कि,

$h=\frac{1}{6} r \Rightarrow r=6 h$

$\therefore V=\frac{1}{3} \pi(6 h)^{2} h=12 \pi h^{3}$

आयतन के बदले आने की दर समय $(t)$ के संदर्भ में दिया गया है,

$\frac{d V}{d t}=12 \pi \frac{d}{d h}(h^{3}) \cdot \frac{d h}{d t}$ [चैन नियम द्वारा]

$=12 \pi(3 h^{2}) \frac{d h}{d t}$

$=36 \pi h^{2} \frac{d h}{d t}$

यह भी दिया गया है कि $\frac{d V}{d t}=12 cm^{3} / s$।

इसलिए, जब $h=4 cm$ हो तो हमें निम्नलिखित प्राप्त होता है:

$ \begin{aligned} & 12=36 \pi(4)^{2} \frac{d h}{d t} \\ & \Rightarrow \frac{d h}{d t}=\frac{12}{36 \pi(16)}=\frac{1}{48 \pi} \end{aligned} $

इसलिए, जब रेत के शंकु की ऊंचाई $4 cm$ हो तो इसकी ऊंचाई $\frac{1}{48 \pi} cm / s$ की दर से बढ़ रही है।

Solution

सीमांत लागत कुल लागत के संबंध में उत्पादन के संबंध में परिवर्तन की दर होती है।

$\therefore$ सीमांत लागत (MC) $=\frac{d C}{d x}=0.007(3 x^{2})-0.003(2 x)+15$

$=0.021 x^{2}-0.006 x+15$

जब $x=17, M C=0.021(17^{2})-0.006(17)+15$ $=0.021(289)-0.006(17)+15$

$=6.069-0.102+15$

$=20.967$

अतः, जब 17 इकाइयों के उत्पादन के समय, सीमांत लागत रु. 20.967 है।

Solution

सीमांत राजस्व बिक्री की इकाइयों की संख्या के संबंध में कुल राजस्व के परिवर्तन की दर होती है।

$\therefore$ सीमांत राजस्व (MR) $=\frac{d R}{d x}=13(2 x)+26=26 x+26$

जब $x=7$,

$M R=26(7)+26=182+26=208$

अतः, आवश्यक सीमांत राजस्व रु. 208 है।

Solution

त्रिज्या $(r)$ के साथ एक वृत्त के क्षेत्रफल ( $A$ ) द्वारा दिया गया है,

$A=\pi r^{2}$

अतः, क्षेत्रफल के संबंध में त्रिज्या $r$ के संबंध में परिवर्तन की दर है

$\frac{d A}{d r}=\frac{d}{d r}(\pi r^{2})=2 \pi r$. $\therefore$ जब $r=6 cm$,

$\frac{d A}{d r}=2 \pi \times 6=12 \pi cm^{2} / s$

अतः, एक वृत्त के क्षेत्रफल के परिवर्तन की आवश्यक दर $12 \pi cm^{2} / s$ है।

सही उत्तर $B$ है।

हल

मार्जिनल राजस्व बिक्री इकाइयों की संख्या के संदर्भ में कुल राजस्व के परिवर्तन दर होता है।

$\therefore$ मार्जिनल राजस्व (MR) $=\frac{d R}{d x}=3(2 x)+36=6 x+36$

$\therefore$ जब $x=15$,

$M R=6(15)+36=90+36=126$

अतः, आवश्यक मार्जिनल राजस्व रु 126 है।

सही उत्तर D है।

हल

मान लीजिए ${ }^{x_1}$ और $x_2$ कोई दो संख्याएँ हैं $\mathbf{R}$ में।

तब, हम निम्नलिखित के अनुसार हैं:

$x_1<x_2 \Rightarrow 3 x_1<3 x_2 \Rightarrow 3 x_1+17<3 x_2+17 \Rightarrow f(x_1)<f(x_2)$

अतः, $f$ फलन $\mathbf{R}$ पर सख्त रूप से बढ़ता है।

अल्टरनेट विधि:

$f(x)=3>0$, $\mathbf{R}$ के प्रत्येक अंतराल में।

अतः, फलन $\mathbf{R}$ पर सख्त रूप से बढ़ता है।

हल

मान लीजिए ${ }^{x_1}$ और $x_2$ कोई दो संख्याएँ हैं $\mathbf{R}$ में।

तब, हम निम्नलिखित के अनुसार हैं:

$x_1<x_2 \Rightarrow 2 x_1<2 x_2 \Rightarrow e^{2 x_1}<e^{2 x_2} \Rightarrow f(x_1)<f(x_2)$

अतः, $f$ फलन $\mathbf{R}$ पर सख्त रूप से बढ़ता है।

हल

दिया गया फलन $f(x)=\sin x$ है।

$\therefore f^{\prime}(x)=\cos x$ (a) प्रत्येक $x \in(0, \frac{\pi}{2})$ के लिए, $\cos x>0$, हमें $f^{\prime}(x)>0$ प्राप्त होता है।

अतः, $f$ फलन $(0, \frac{\pi}{2})$ में सख्त रूप से बढ़ता है।

(b) प्रत्येक $x \in(\frac{\pi}{2}, \pi)$ के लिए, $\cos x<0$, हमें $f^{\prime}(x)<0$ प्राप्त होता है।

अतः, $f$ फलन $(\frac{\pi}{2}, \pi)$ में सख्त रूप से घटता है।

(c) (a) और (b) में प्राप्त नतीजों से स्पष्ट है कि $f$ फलन $(0, \pi)$ में न बढ़ता है और न ही घटता है।

हल

दिया गया फलन $f(x)=2 x^{2}-3 x$ है।

$f^{\prime}(x)=4 x-3$

$\therefore f^{\prime}(x)=0 \Rightarrow x=\frac{3}{4}$

अब, बिंदु $\frac{3}{4}$ वास्तविक रेखा को दो अलग-अलग अंतराल में विभाजित करता है अर्थात, $(-\infty, \frac{3}{4})$ और $(\frac{3}{4}, \infty)$।

अंतराल $(-\infty, \frac{3}{4}), f^{\prime}(x)=4 x-3<0$।

अतः, दी गई फलन $(f)$ अंतराल $(-\infty, \frac{3}{4})$ में सख्त घटता है।

अंतराल $(\frac{3}{4}, \infty), f^{\prime}(x)=4 x-3>0$।

अतः, दी गई फलन $(f)$ अंतराल $(\frac{3}{4}, \infty)$ में सख्त बढ़ता है।

हल

दिया गया फलन $f(x)=2 x^{3}-3 x^{2}-36 x+7$ है।

$f^{\prime}(x)=6 x^{2}-6 x-36=6(x^{2}-x-6)=6(x+2)(x-3)$

$\therefore f^{\prime}(x)=0 \Rightarrow x=-2,3$

बिंदु $x=-2$ और $x=3$ वास्तविक रेखा को तीन अलग-अलग अंतराल में विभाजित करते हैं अर्थात, $(-\infty,-2),(-2,3)$, और $(3, \infty)$।

अंतराल $(-\infty,-2)$ और $(3, \infty), f^{\prime}(x)$ धनात्मक होता है जबकि अंतराल $(-2,3), f^{\prime}(x)$ ऋणात्मक होता है।

अतः, दिया गया फलन $(f)$ अंतराल $(-\infty,-2)$ और $(3, \infty)$ में सख्त बढ़ता है, जबकि फलन $(f)$ अंतराल $(-2,3)$ में सख्त घटता है।

हल

(a) हमें दिया गया है,

$f(x)=x^{2}+2 x-5$

$\therefore f^{\prime}(x)=2 x+2$

अब,

$f^{\prime}(x)=0 \Rightarrow x=-1$

बिंदु $x=-1$ वास्तविक रेखा को दो अलग-अलग अंतराल में विभाजित करता है, अर्थात $(-\infty,-1)$ और $(-1, \infty)$।

अंतराल $(-\infty,-1)$ में, $f^{\prime}(x)=2 x+2<0$।

$\therefore f$ अंतराल $(-\infty,-1)$ में सख्त घटती है।

इसलिए, $f$ बिंदु $x<-1$ के लिए सख्त घटती है।

अंतराल $(-1, \infty)$ में, $f^{\prime}(x)=2 x+2>0$।

$\therefore f$ अंतराल $(-1, \infty)$ में सख्त बढ़ती है।

इसलिए, $f$ बिंदु $x>-1$ के लिए सख्त बढ़ती है।

(b) हमें दिया गया है,

$f(x)=10-6 x-2 x^{2}$

$\therefore f^{\prime}(x)=-6-4 x$

अब,

$f^{\prime}(x)=0 \Rightarrow x=-\frac{3}{2}$

बिंदु $x=-\frac{3}{2}$ वास्तविक रेखा को दो अलग-अलग अंतराल में विभाजित करता है

अर्थात $(-\infty,-\frac{3}{2})$ और $(-\frac{3}{2}, \infty)$।

अंतराल $(-\infty,-\frac{3}{2})$ अर्थात जब $x<-\frac{3}{2}, f^{\prime}(x)=-6-4 x<0$।

$\therefore f$ बिंदु $x<-\frac{3}{2}$ के लिए सख्त बढ़ती है।

अंतराल $(-\frac{3}{2}, \infty)$ अर्थात जब $x>-\frac{3}{2}, f^{\prime}(x)=-6-4 x<0$।

$\therefore f$ बिंदु $x>-\frac{3}{2}$ के लिए सख्त घटती है।

(c) हमें दिया गया है,

$f(x)=-2 x^{3}-9 x^{2}-12 x+1$

$\therefore f^{\prime}(x)=-6 x^{2}-18 x-12=-6(x^{2}+3 x+2)=-6(x+1)(x+2)$

अब,

$f^{\prime}(x)=0 \Rightarrow x=-1$ और $x=-2$

बिंदु $x=-1$ और $x=-2$ वास्तविक रेखा को तीन अलग-अलग अंतराल में विभाजित करते हैं

अर्थात $(-\infty,-2),(-2,-1)$, और $(-1, \infty)$।

अंतराल $(-\infty,-2)$ और $(-1, \infty)$ अर्थात जब $x<-2$ और $x>-1$,

$f^{\prime}(x)=-6(x+1)(x+2)<0$। $\therefore f$ बिंदु $x<-2$ और $x>-1$ के लिए सख्त घटती है।

अब, अंतराल $(-2,-1)$ अर्थात जब $-2<x<-1, f^{\prime}(x)=-6(x+1)(x+2)>0$।

$\therefore f$ बिंदु $-2<x<-1$ के लिए सख्त बढ़ती है।

(d) हमें दिया गया है,

$ \begin{aligned} & f(x)=6-9 x-x^{2} \\ & \therefore f^{\prime}(x)=-9-2 x \end{aligned} $

अब, $f^{\prime}$

$(x)=0$ देता है $x=-\frac{9}{2}$

बिंदु $x=-\frac{9}{2}$ वास्तविक रेखा को दो अलग-अलग अंतराल में विभाजित करता है अर्थात,

$(-\infty,-\frac{9}{2})$ और $(-\frac{9}{2}, \infty)$।

अंतराल $(-\infty,-\frac{9}{2})$ अर्थात, $x<-\frac{9}{2}$ के लिए, $f^{\prime}(x)=-9-2 x>0$।

$\therefore f$ $x<-\frac{9}{2}$ के लिए सख्त रूप से बढ़ती है।

अंतराल $(-\frac{9}{2}, \infty)$ अर्थात, $x>-\frac{9}{2}$ के लिए, $f^{\prime}(x)=-9-2 x<0$। $\therefore f$ $x>-\frac{9}{2}$ के लिए सख्त रूप से घटती है।

(e) हमारे पास,

$ \begin{aligned} f(x)= & (x+1)^{3}(x-3)^{3} \\ f^{\prime}(x) & =3(x+1)^{2}(x-3)^{3}+3(x-3)^{2}(x+1)^{3} \\ & =3(x+1)^{2}(x-3)^{2}[x-3+x+1] \\ & =3(x+1)^{2}(x-3)^{2}(2 x-2) \\ & =6(x+1)^{2}(x-3)^{2}(x-1) \end{aligned} $

अब,

$f^{\prime}(x)=0 \Rightarrow x=-1,3,1$

बिंदु $x=-1, x=1$, और $x=3$ वास्तविक रेखा को चार अलग-अलग अंतराल में विभाजित करते हैं

अर्थात, $(-\infty,-1),(-1,1),(1,3)$, और $(3, \infty)$।

अंतराल $(-\infty,-1)$ और $(-1,1)$ में, $f^{\prime}(x)=6(x+1)^{2}(x-3)^{2}(x-1)<0$।

$\therefore f$ अंतराल $(-\infty,-1)$ और $(-1,1)$ में सख्त रूप से घटती है।

अंतराल $(1,3)$ और $(3, \infty)$ में, $f^{\prime}(x)=6(x+1)^{2}(x-3)^{2}(x-1)>0$।

$\therefore f$ अंतराल $(1,3)$ और $(3, \infty)$ में सख्त रूप से बढ़ती है।

Solution

हमारे पास,

$ \begin{aligned} & y=\log (1+x)-\frac{2 x}{2+x} \\ & \therefore \frac{d y}{d x}=\frac{1}{1+x}-\frac{(2+x)(2)-2 x(1)}{(2+x)^{2}}=\frac{1}{1+x}-\frac{4}{(2+x)^{2}}=\frac{x^{2}}{(2+x)^{2}} \end{aligned} $

अब, $\frac{d y}{d x}=0$

$\Rightarrow \frac{x^{2}}{(2+x)^{2}}=0$

$\Rightarrow x^{2}=0 \quad[(2+x) \neq 0$ क्योंकि $x>-1]$

$\Rightarrow x=0$

क्योंकि $x>-1$, बिंदु $x=0$ डोमेन $(-1, \infty)$ को दो अलग-अलग अंतराल में विभाजित करता है अर्थात, $-1<$ $x<0$ और $x>0$।

जब $-1<x<0$, हमारे पास:

$x<0 \Rightarrow x^{2}>0$

$x>-1 \Rightarrow(2+x)>0 \Rightarrow(2+x)^{2}>0$

$\therefore y^{\prime}=\frac{x^{2}}{(2+x)^{2}}>0$

इसके अलावा, जब $x>0$:

$x>0 \Rightarrow x^{2}>0,(2+x)^{2}>0$

$\therefore y^{\prime}=\frac{x^{2}}{(2+x)^{2}}>0$

इसलिए, फलन $f$ इस डोमेन में बढ़ता है।

हल

हमारे पास,

$y=[x(x-2)]^{2}=[x^{2}-2 x]^{2}$

$\therefore \frac{d y}{d x}=y^{\prime}=2(x^{2}-2 x)(2 x-2)=4 x(x-2)(x-1)$

$\therefore \frac{d y}{d x}=0 \Rightarrow x=0, x=2, x=1$।

बिंदु $x=0, x=1$, और $x=2$ वास्तविक रेखा को चार अलग-अलग अंतराल में विभाजित करते हैं, अर्थात $(-\infty, 0),(0,1)(1,2)$, और $(2, \infty)$।

अंतराल $(-\infty, 0)$ और $(1,2)$ में $\frac{d y}{d x}<0$।

$\therefore y$ अंतराल $(-\infty, 0)$ और $(1,2)$ में सख्ती से घटता है।

हालांकि, अंतराल $(0,1)$ और $(2, \infty)$ में $\frac{d y}{d x}>0$।

$\therefore y$ अंतराल $(0,1)$ और $(2, \infty)$ में सख्ती से बढ़ता है।

$\therefore y$ $0<x<1$ और $x>2$ के लिए सख्ती से बढ़ता है।

हल

हमारे पास,

$ \begin{aligned} & y=\frac{4 \sin \theta}{(2+\cos \theta)}-\theta \\ & \begin{aligned} \therefore \frac{d y}{d x} & =\frac{(2+\cos \theta)(4 \cos \theta)-4 \sin \theta(-\sin \theta)}{(2+\cos \theta)^{2}}-1 \\ \quad & \frac{8 \cos \theta+4 \cos ^{2} \theta+4 \sin ^{2} \theta}{(2+\cos \theta)^{2}}-1 \\ \quad & \frac{8 \cos \theta+4}{(2+\cos \theta)^{2}}-1 \end{aligned} \end{aligned} $

अब, $\frac{d y}{d x}=0$।

$\Rightarrow \frac{8 \cos \theta+4}{(2+\cos \theta)^{2}}=1$

$\Rightarrow 8 \cos \theta+4=4+\cos ^{2} \theta+4 \cos \theta$

$\Rightarrow \cos ^{2} \theta-4 \cos \theta=0$

$\Rightarrow \cos \theta(\cos \theta-4)=0$

$\Rightarrow \cos \theta=0$ या $\cos \theta=4$

क्योंकि $\cos \theta \neq 4, \cos \theta=0$।

$\cos \theta=0 \Rightarrow \theta=\frac{\pi}{2}$

अब,

$\frac{d y}{d x}=\frac{8 \cos \theta+4-(4+\cos ^{2} \theta+4 \cos \theta)}{(2+\cos \theta)^{2}}=\frac{4 \cos \theta-\cos ^{2} \theta}{(2+\cos \theta)^{2}}=\frac{\cos \theta(4-\cos \theta)}{(2+\cos \theta)^{2}}$

अंतराल $(0, \frac{\pi}{2})$ में, हमें $\cos \theta>0$ मिलता है। अतः, $4>\cos \theta \Rightarrow 4-\cos \theta>0$।

$\therefore \cos \theta(4-\cos \theta)>0$ और भी $(2+\cos \theta)^{2}>0$ है

$\Rightarrow \frac{\cos \theta(4-\cos \theta)}{(2+\cos \theta)^{2}}>0$

$\Rightarrow \frac{d y}{d x}>0$

अतः, $y$ अंतराल $(0, \frac{\pi}{2})$ में सख्त रूप से बढ़ती है।

इसके अतिरिक्त, दी गई फलन $x=0$ और $x=\frac{\pi}{2}$ पर सतत है।

अतः, $y$ अंतराल $[0, \frac{\pi}{2}]$ में बढ़ती है।

हल

दिया गया फलन $f(x)=\log x$ है।

$\therefore f^{\prime}(x)=\frac{1}{x}$

स्पष्ट रूप से, $x>0$ के लिए $f^{\prime}(x)=\frac{1}{x}>0$ है।

अतः, $f(x)=\log x$ अंतराल $(0, \infty)$ में सख्त रूप से बढ़ता है।

हल

दिया गया फलन $f(x)=x^{2}-x+1$ है।

$\therefore f^{\prime}(x)=2 x-1$

अब, $f^{\prime}(x)=0 \Rightarrow x=\frac{1}{2}$ है।

बिंदु $\frac{1}{2}$ अंतराल $(-1,1)$ को दो अलग-अलग अंतरालों में विभाजित करता है

अर्थात, $(-1, \frac{1}{2})$ और $(\frac{1}{2}, 1)$।

अब, अंतराल $(-1, \frac{1}{2})$ में, $f^{\prime}(x)=2 x-1<0$ है।

अतः, $f$ अंतराल $(-1, \frac{1}{2})$ में सख्त रूप से घटता है।

हालांकि, अंतराल $(\frac{1}{2}, 1)$ में, $f^{\prime}(x)=2 x-1>0$ है।

अतः, $f$ अंतराल $(\frac{1}{2}, 1)$ में सख्त रूप से बढ़ता है।

अतः, $f$ अंतराल $(-1,1)$ में न तो सख्त रूप से बढ़ता है और न ही घटता है।

हल

(A) मान लीजिए $f_1(x)=\cos x$।

$\therefore f_1^{\prime}(x)=-\sin x$

अंतराल $(0, \frac{\pi}{2})$ में, $f_1^{\prime}(x)=-\sin x<0$ है।

$\therefore f_1(x)=\cos x$ अंतराल $(0, \frac{\pi}{2})$ में सख्त रूप से घटता है।

(B) मान लीजिए $f_2(x)=\cos 2 x$.

$\therefore f_2^{\prime}(x)=-2 \sin 2 x$

अब, $0<x<\frac{\pi}{2} \Rightarrow 0<2 x<\pi \Rightarrow \sin 2 x>0 \Rightarrow-2 \sin 2 x<0$

$\therefore f_2^{\prime}(x)=-2 \sin 2 x<0$ अंतराल $(0, \frac{\pi}{2})$ पर

$\therefore f_2(x)=\cos 2 x$ अंतराल $(0, \frac{\pi}{2})$ में सख्त घटती है।

(C) मान लीजिए $f_3(x)=\cos 3 x$.

$\therefore f_3^{\prime}(x)=-3 \sin 3 x$

अब, $f_3^{\prime}(x)=0$.

$\Rightarrow \sin 3 x=0 \Rightarrow 3 x=\pi$, क्योंकि $x \in(0, \frac{\pi}{2})$

$\Rightarrow x=\frac{\pi}{3}$

बिंदु $x=\frac{\pi}{3}$ अंतराल $(0, \frac{\pi}{2})$ को दो अलग-अलग अंतराल में विभाजित करता है

अर्थात, $0(0, \frac{\pi}{3})$ और $(\frac{\pi}{3}, \frac{\pi}{2})$।

अब, अंतराल $(0, \frac{\pi}{3}), f_3(x)=-3 \sin 3 x<0[.$ क्योंकि $.0<x<\frac{\pi}{3} \Rightarrow 0<3 x<\pi]$.

$\therefore f_3$ अंतराल $(0, \frac{\pi}{3})$ में सख्त घटती है।

हालांकि, अंतराल $(\frac{\pi}{3}, \frac{\pi}{2}), f_3(x)=-3 \sin 3 x>0[.$ क्योंकि $.\frac{\pi}{3}<x<\frac{\pi}{2} \Rightarrow \pi<3 x<\frac{3 \pi}{2}]$. $\therefore f_3$ अंतराल $(\frac{\pi}{3}, \frac{\pi}{2})$ में सख्त बढ़ती है।

इसलिए, $f_3$ अंतराल $(0, \frac{\pi}{2})$ में न तो बढ़ती है और न ही घटती है।

(D) मान लीजिए $f_4(x)=\tan x$.

$\therefore f_4^{\prime}(x)=\sec ^{2} x$

अंतराल $(0, \frac{\pi}{2}), f_4^{\prime}(x)=\sec ^{2} x>0$.

$\therefore f_4$ अंतराल $(0, \frac{\pi}{2})$ में सख्त बढ़ती है।

इसलिए, फलन $\cos x$ और $\cos 2 x$ अंतराल $(0, \frac{\pi}{2})$ में सख्त घटते हैं। इसलिए, सही उत्तर A और B हैं।

हल

हम जानते हैं, $f(x)=x^{100}+\sin x-1$

$\therefore f^{\prime}(x)=100 x^{99}+\cos x$

अंतराल $(0,1), \cos x>0$ और $100 x^{99}>0$.

$\therefore f^{\prime}(x)>0$.

इसलिए, फलन $f$ अंतराल $(0,1)$ में सख्त बढ़ती है।

अंतराल $(\frac{\pi}{2}, \pi), \cos x<0$ और $100 x^{99}>0$ है। इसके अलावा, $100 x^{99}>\cos x$ भी है।

$\therefore f^{\prime}(x)>0$ अंतराल $(\frac{\pi}{2}, \pi)$ में है।

इसलिए, फलन $f$ अंतराल $(\frac{\pi}{2}, \pi)$ में सख्त रूप से बढ़ रहा है।

अंतराल $(0, \frac{\pi}{2}), \cos x>0$ और $100 x^{99}>0$ है।

$\therefore 100 x^{99}+\cos x>0$

$\Rightarrow f^{\prime}(x)>0$ अंतराल $(0, \frac{\pi}{2})$ पर है

$\therefore f$ अंतराल $(0, \frac{\pi}{2})$ में सख्त रूप से बढ़ रहा है।

इसलिए, फलन $f$ कोई भी अंतराल में सख्त रूप से घट रहा नहीं है।

सही उत्तर D है।

हल

हम जानते हैं, $f(x)=x^{2}+a x+1$

$\therefore f^{\prime}(x)=2 x+a$

अब, फलन $f$ अंतराल $(1,2)$ में बढ़ रहा होगा, यदि $f^{\prime}(x)>0$ अंतराल $(1,2)$ में है।

$f^{\prime}(x)>0$

$\Rightarrow 2 x+a>0$

$\Rightarrow 2 x>-a$

$\Rightarrow \quad x>\frac{-a}{2}$

इसलिए, हमें ऐसे न्यूनतम मान का पता लगाना होगा जिसके लिए

$x>\frac{-a}{2}$, जब $x \in(1,2)$ हो।

$\Rightarrow x>\frac{-a}{2}$ (जब $1<x<2)$

इसलिए, फलन $f$ के लिए अंतराल $(1,2)$ पर बढ़ता होने के लिए $a$ का न्यूनतम मान निम्नलिखित द्वारा दिया गया है,

$\frac{-a}{2}=1$

$\frac{-a}{2}=1 \Rightarrow a=-2$

इसलिए, $a$ के आवश्यक मान -2 है।

हल

हम जानते हैं,

$f(x)=x+\frac{1}{x}$

$\therefore f^{\prime}(x)=1-\frac{1}{x^{2}}$

अब,

$f^{\prime}(x)=0 \Rightarrow \frac{1}{x^{2}}=1 \Rightarrow x= \pm 1$

बिंदु $x=1$ और $x=-1$ वास्तविक रेखा को तीन अलग-अलग अंतराल में विभाजित करते हैं, अर्थात,

$(-\infty,-1),(-1,1)$, और $(1, \infty)$।

अंतराल $(-1,1)$ में यह देखा जाता है कि:

$-1<x<1$

$\Rightarrow x^{2}<1$

$\Rightarrow 1<\frac{1}{x^{2}}, x \neq 0$

$\Rightarrow 1-\frac{1}{x^{2}}<0, x \neq 0$

$\therefore f^{\prime}(x)=1-\frac{1}{x^{2}}<0$ अंतराल $(-1,1) \sim{0}$ पर है।

$\therefore f$ अंतराल $(-1,1) \sim{0}$ पर सख्त घटती है।

अंतराल $(-\infty,-1)$ और $(1, \infty)$ में, यह देखा गया है कि: $x<-1$ या $1<x$

$\Rightarrow x^{2}>1$

$\Rightarrow 1>\frac{1}{x^{2}}$

$\Rightarrow 1-\frac{1}{x^{2}}>0$

$\therefore f^{\prime}(x)=1-\frac{1}{x^{2}}>0$ अंतराल $(-\infty,-1)$ और $(1, \infty)$ पर।

$\therefore f$ अंतराल $(-\infty, 1)$ और $(1, \infty)$ पर सख्त बढ़ती है।

इसलिए, फलन $f$ अंतराल $\mathbf{I}$ पर सख्त बढ़ती है जो $(-1,1)$ से अलग है। इसलिए, दिए गए परिणाम की साबित कर दिया गया है।

हल

हम जानते हैं,

$f(x)=\log \sin x$

$\therefore f^{\prime}(x)=\frac{1}{\sin x} \cos x=\cot x$

अंतराल $(0, \frac{\pi}{2})$ में, $f^{\prime}(x)=\cot x>0$।

$\therefore f$ अंतराल $(0, \frac{\pi}{2})$ में सख्त बढ़ती है।

अंतराल $(\frac{\pi}{2}, \pi)$ में, $f^{\prime}(x)=\cot x<0$।

$\therefore f$ अंतराल $(\frac{\pi}{2}, \pi)$ में सख्त घटती है।

हल

हम जानते हैं,

$f(x)=\log \cos x$

$\therefore f^{\prime}(x)=\frac{1}{\cos x}(-\sin x)=-\tan x$

अंतराल $(0, \frac{\pi}{2})$ में, $\tan x>0 \Rightarrow-\tan x<0$।

$\therefore f^{\prime}(x)<0$ अंतराल $(0, \frac{\pi}{2})$ पर

$\therefore f$ अंतराल $(0, \frac{\pi}{2})$ पर सख्त घटती है।

अंतराल $(\frac{\pi}{2}, \pi)$ में, $\tan x<0 \Rightarrow-\tan x>0$।

$\therefore f^{\prime}(x)>0$ अंतराल $(\frac{\pi}{2}, \pi)$ पर $\therefore f$ अंतराल $(\frac{\pi}{2}, \pi)$ पर सख्त बढ़ती है।

हल

हम जानते हैं,

$f(x)=x^{3}-3 x^{2}+3 x-100$

$ \begin{aligned} f^{\prime}(x) & =3 x^{2}-6 x+3 \ \end{aligned} `

& =3(x^{2}-2 x+1) \\ & =3(x-1)^{2} \end{aligned} $

किसी भी $x \in \mathbf{R},(x-1)^{2}>0$।

अतः, $f^{\prime}(x)$ वास्तविक संख्या में हमेशा धनात्मक होता है।

इसलिए, दी गई फलन $(f)$ वास्तविक संख्या में बढ़ता है।

हल

हमें दिया गया है,

$y=x^{2} e^{-x}$ $\therefore \frac{d y}{d x}=2 x e^{-x}-x^{2} e^{-x}=x e^{-x}(2-x)$

अब, $\frac{d y}{d x}=0$.

$\Rightarrow x=0$ और $x=2$

बिंदु $x=0$ और $x=2$ वास्तविक रेखा को तीन अलग-अलग अंतराल में विभाजित करते हैं

अर्थात, $(-\infty, 0),(0,2)$, और $(2, \infty)$।

अंतराल $(-\infty, 0)$ और $(2, \infty)$ में $f^{\prime}(x)<0$ क्योंकि $e^{-x}$ हमेशा धनात्मक होता है।

$\therefore f$ अंतराल $(-\infty, 0)$ और $(2, \infty)$ पर घटता है।

अंतराल $(0,2)$ में $f^{\prime}(x)>0$।

$\therefore f$ अंतराल $(0,2)$ पर सख्ती से बढ़ता है।

इसलिए, $f$ अंतराल $(0,2)$ में सख्ती से बढ़ता है।

सही उत्तर D है।

हल

(i) दिया गया फलन $f(x)=(2 x-1)^{2}+3$ है।

यह देखा जा सकता है कि $(2 x-1)^{2} \geq 0$ प्रत्येक $x \in \mathbf{R}$ के लिए।

इसलिए, $f(x)=(2 x-1)^{2}+3 \geq 3$ प्रत्येक $x \in \mathbf{R}$ के लिए।

$f$ का न्यूनतम मान जब $2 x-1=0$ होता है।

$2 x-1=0$

$ x=\frac{1}{2} $

$\square$ $f$ का न्यूनतम मान $f(\frac{1}{2})=(2 \cdot \frac{1}{2}-1)^{2}+3=3$

अतः, फलन $f$ का अधिकतम मान नहीं है।

(ii) दिया गया फलन $f(x)=9 x^{2}+12 x+2=(3 x+2)^{2}-2$ है।

यह देखा जा सकता है कि $(3 x+2)^{2} \geq 0$ प्रत्येक $x \in \mathbf{R}$ के लिए।

इसलिए, $f(x)=(3 x+2)^{2}-2 \geq-2$ प्रत्येक $x \in \mathbf{R}$ के लिए।

$f$ का न्यूनतम मान जब $3 x+2=0$ होता है।

$3 x+2=0 \Rightarrow x=\frac{-2}{3}$

$\square$ $f$ का न्यूनतम मान $f(-\frac{2}{3})=(3(\frac{-2}{3})+2)^{2}-2=-2$

अतः, फलन $f$ का अधिकतम मान नहीं है।

(iii) दिया गया फलन $f(x)=-(x-1)^{2}+10$ है।

यह देखा जा सकता है कि $(x-1)^{2} \geq 0$ प्रत्येक $x \in \mathbf{R}$ के लिए।

इसलिए, $f(x)=-(x-1)^{2}+10 \leq 10$ प्रत्येक $x \in \mathbf{R}$ के लिए।

$f$ का अधिकतम मान जब $(x-1)=0$ होता है।

$(x-1)=0 \Rightarrow x=1$

$\square$ $f$ का अधिकतम मान $f(1)=-(1-1)^{2}+10=10$

अतः, फलन $f$ का न्यूनतम मान नहीं है।

(iv) दिया गया फलन $g(x)=x^{3}+1$ है।

अतः, फलन $g$ का अधिकतम और न्यूनतम मान दोनों ही नहीं है।

हल

(i) $f(x)=|x+2|-1$

हम जानते हैं कि $|x+2| \geq 0$ प्रत्येक $x \in \mathbf{R}$ के लिए।

इसलिए, $f(x)=|x+2|-1 \geq-1$ प्रत्येक $x \square \mathbf{R}$ के लिए।

$f$ का न्यूनतम मान जब $|x+2|=0$ होता है।

$|x+2|=0$

$\Rightarrow x=-2$

$\square$ न्यूनतम मान $f=f(-2)=|-2+2|-1=-1$

इसलिए, फलन $f$ का अधिकतम मान नहीं होता।

(ii) $g(x)=-|x+1|+3$

हम जानते हैं कि $-|x+1| \leq 0$ प्रत्येक $x \square \mathbf{R}$ के लिए।

इसलिए, $g(x)=-|x+1|+3 \leq 3$ प्रत्येक $x \square \mathbf{R}$ के लिए।

$g$ का अधिकतम मान जब $|x+1|=0$ होता है।

$|x+1|=0$

$\Rightarrow x=-1$

$\square$ अधिकतम मान $g=g(-1)=-|-1+1|+3=3$

इसलिए, फलन $g$ का न्यूनतम मान नहीं होता। (iii) $h(x)=\sin 2 x+5$

हम जानते हैं कि $-1 \leq \sin 2 x \leq 1$।

$\square-1+5 \leq \sin 2 x+5 \leq 1+5$

$\square 4 \leq \sin 2 x+5 \leq 6$

इसलिए, $h$ के अधिकतम और न्यूनतम मान क्रमशः 6 और 4 हैं।

(iv) $f(x)=|\sin 4 x+3|$

हम जानते हैं कि $-1 \leq \sin 4 x \leq 1$।

$\square 2 \leq \sin 4 x+3 \leq 4$

$\square 2 \leq^{|\sin 4 x+3|} \leq 4$

इसलिए, $f$ के अधिकतम और न्यूनतम मान क्रमशः 4 और 2 हैं।

(v) $h(x)=x+1, x \square(-1,1)$

यहाँ, यदि एक बिंदु $x_0$ -1 के सबसे करीब हो, तो हम जानते हैं कि $\frac{x_0}{2}+1<x_0+1$ सभी $x_0 \square(-1,1)$ के लिए।

इसके अलावा, यदि $x_1$ 1 के सबसे करीब हो, तो $x_1+1<\frac{x_1+1}{2}+1$ सभी $x_1 \square(-1,1)$ के लिए।

इसलिए, फलन $h(x)$ के अंतराल $(-1,1)$ में कोई अधिकतम या न्यूनतम मान नहीं होता।

Solution

(i) $f(x)=x^{2}$

$\therefore f^{\prime}(x)=2 x$

अब,

$f^{\prime}(x)=0 \Rightarrow x=0$

इसलिए, $x=0$ एकमात्र ऐसा क्रिटिकल बिंदु है जो $f$ के लोकल मैक्सिमम या लोकल मिनिमम के बिंदु हो सकता है।

हमें $f^{\prime \prime}(0)=2$ है, जो धनात्मक है।

इसलिए, दूसरे अवकलज परीक्षण के अनुसार, $x=0$ एक स्थानीय न्यूनतम बिंदु है और $f$ के $x=0$ पर स्थानीय न्यूनतम मान $f(0)=0$ है।

(ii) $g(x)=x^{3}-3 x$

$\therefore g^{\prime}(x)=3 x^{2}-3$

अब,

$g^{\prime}(x)=0 \Rightarrow 3 x^{2}=3 \Rightarrow x= \pm 1$

$g^{\prime}(x)=6 x$

$g^{\prime}(1)=6>0$

$g^{\prime}(-1)=-6<0$

दूसरे अवकलज परीक्षण के अनुसार, $x=1$ एक स्थानीय न्यूनतम बिंदु है और $g$ के $x=1$ पर स्थानीय न्यूनतम मान $g(1)=1^{3}-3=1-3=-2$ है। हालांकि, $x=-1$ एक स्थानीय उच्चिष्ठ बिंदु है और $g$ के $x=-1$ पर स्थानीय उच्चिष्ठ मान $g(1)=(-1)^{3}-3(-1)=-1+3=2$ है।

(iii) $h(x)=\sin x+\cos x, 0<x<\frac{\pi}{2}$

$\therefore h^{\prime}(x)=\cos x-\sin x$

$h^{\prime}(x)=0 \Rightarrow \sin x=\cos x \Rightarrow \tan x=1 \Rightarrow x=\frac{\pi}{4} \in(0, \frac{\pi}{2})$

$h^{\prime \prime}(x)=-\sin x-\cos x=-(\sin x+\cos x)$

$h^{\prime \prime}(\frac{\pi}{4})=-(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}})=-\frac{2}{\sqrt{2}}=-\sqrt{2}<0$

इसलिए, दूसरे अवकलज परीक्षण के अनुसार, $x=\frac{\pi}{4}$ एक स्थानीय उच्चिष्ठ बिंदु है और $h$ के $x=\frac{\pi}{4}$ पर स्थानीय उच्चिष्ठ मान $h(\frac{\pi}{4})=\sin \frac{\pi}{4}+\cos \frac{\pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}$ है।

(iv) $f(x)=\sin x-\cos x, 0<x<2 \pi$

$\therefore f^{\prime}(x)=\cos x+\sin x$

$f^{\prime}(x)=0 \Rightarrow \cos x=-\sin x \Rightarrow \tan x=-1 \Rightarrow x=\frac{3 \pi}{4}, \frac{7 \pi}{4} \in(0,2 \pi)$

$f^{\prime \prime}(x)=-\sin x+\cos x$

$f^{\prime \prime}(\frac{3 \pi}{4})=-\sin \frac{3 \pi}{4}+\cos \frac{3 \pi}{4}=-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2}>0$

$f^{\prime \prime}(\frac{7 \pi}{4})=-\sin \frac{7 \pi}{4}+\cos \frac{7 \pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}>0$

इसलिए, दूसरे अवकलज परीक्षण के अनुसार, $x=\frac{3 \pi}{4}$ एक स्थानीय उच्चिष्ठ बिंदु है और $f$ के $x=\frac{3 \pi}{4}$ पर स्थानीय उच्चिष्ठ मान

$f(\frac{3 \pi}{4})=\sin \frac{3 \pi}{4}-\cos \frac{3 \pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}$ है। हालांकि, $x=\frac{7 \pi}{4}$ एक स्थानीय न्यूनतम बिंदु है और

the local minimum value of $f$ at $x=\frac{7 \pi}{4}$ is $f(\frac{7 \pi}{4})=\sin \frac{7 \pi}{4}-\cos \frac{7 \pi}{4}=-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2}$.

(v) $f(x)=x^{3}-6 x^{2}+9 x+15$

$\therefore f^{\prime}(x)=3 x^{2}-12 x+9$

$f^{\prime}(x)=0 \Rightarrow 3(x^{2}-4 x+3)=0$

$\Rightarrow 3(x-1)(x-3)=0$

$\Rightarrow x=1,3$

Now, $f^{\prime \prime}$

$(x)=6 x-12=6(x-2)$

$f^{\prime \prime}(1)=6(1-2)=-6<0$

$f^{\prime \prime}(3)=6(3-2)=6>0$

Therefore, by second derivative test, $x=1$ is a point of local maxima and the local maximum value of $f$ at $x=1$ is $f(1)=1-6+9+15=19$. However, $x=3$ is a point of local minima and the local minimum value of $f$ at $x=3$ is $f(3)=27-54+27+15=$ 15.

(vi) $g(x)=\frac{x}{2}+\frac{2}{x}, x>0$

$\therefore g^{\prime}(x)=\frac{1}{2}-\frac{2}{x^{2}}$

Now,

$g^{\prime}(x)=0$ gives $\frac{2}{x^{2}}=\frac{1}{2} \Rightarrow x^{2}=4 \Rightarrow x= \pm 2$

Since $x>0$, we take $x=2$.

Now,

$g^{\prime \prime}(x)=\frac{4}{x^{3}}$

$g^{\prime \prime}(2)=\frac{4}{2^{3}}=\frac{1}{2}>0$

Therefore, by second derivative test, $x=2$ is a point of local minima and the local

minimum value of $g$ at $x=2$ is $g(2)=\frac{2}{2}+\frac{2}{2}=1+1=2$.

(vii) $g(x)=\frac{1}{x^{2}+2}$

$\therefore g^{\prime}(x)=\frac{-(2 x)}{(x^{2}+2)^{2}}$

$g^{\prime}(x)=0 \Rightarrow \frac{-2 x}{(x^{2}+2)^{2}}=0 \Rightarrow x=0$

Now, for values close to $x=0$ and to the left of $0, g^{\prime}(x)>0$. Also, for values close to $x=$ 0 and to the right of $0, g^{\prime}(x)<0$.

Therefore, by first derivative test, $x=0$ is a point of local maxima and the local maximum value of $g(0)$ is $\frac{1}{0+2}=\frac{1}{2}$.

(viii) $f(x)=x \sqrt{1-x}, x>0$

$\therefore f^{\prime}(x)=\sqrt{1-x}+x \cdot \frac{1}{2 \sqrt{1-x}}(-1)=\sqrt{1-x}-\frac{x}{2 \sqrt{1-x}}$

$=\frac{2(1-x)-x}{2 \sqrt{1-x}}=\frac{2-3 x}{2 \sqrt{1-x}}$

$f^{\prime}(x)=0 \Rightarrow \frac{2-3 x}{2 \sqrt{1-x}}=0 \Rightarrow 2-3 x=0 \Rightarrow x=\frac{2}{3}$

$f^{\prime \prime}(x)=\frac{1}{2}[\frac{\sqrt{1-x}(-3)-(2-3 x)(\frac{-1}{2 \sqrt{1-x}})}{1-x}]$

$=\frac{\sqrt{1-x}(-3)+(2-3 x)(\frac{1}{2 \sqrt{1-x}})}{2(1-x)}$

$=\frac{-6(1-x)+(2-3 x)}{4(1-x)^{\frac{3}{2}}}$

$=\frac{3 x-4}{4(1-x)^{\frac{3}{2}}}$

$f^{\prime \prime}(\frac{2}{3})=\frac{3(\frac{2}{3})-4}{4(1-\frac{2}{3})^{\frac{3}{2}}}=\frac{2-4}{4(\frac{1}{3})^{\frac{3}{2}}}=\frac{-1}{2(\frac{1}{3})^{\frac{3}{2}}}<0$

इसलिए, द्वितीय अवकलज परीक्षण के अनुसार, $x=\frac{2}{3}$ एक स्थानीय उच्चिष्ठ बिंदु है और $f$ के $x=\frac{2}{3}$ पर स्थानीय उच्चिष्ठ मान है $f(\frac{2}{3})=\frac{2}{3} \sqrt{1-\frac{2}{3}}=\frac{2}{3} \sqrt{\frac{1}{3}}=\frac{2}{3 \sqrt{3}}=\frac{2 \sqrt{3}}{9}$.

हल

i. हम जानते हैं,

$f(x)=e^{x}$

$\therefore f^{\prime}(x)=e^{x}$

अब, यदि $f^{\prime}(x)=0$, तो $e^{x}=0$. लेकिन, समाकलन फलन कभी भी किसी भी $x$ के मान के लिए 0 नहीं हो सकता।

इसलिए, कोई भी $c \in \mathbf{R}$ ऐसा नहीं है जैसे कि $f^{\prime}(c)=0$.

इसलिए, फलन $f$ उच्चिष्ठ या निम्निष्ठ नहीं हो सकता।

ii. हम जानते हैं,

$g(x)=\log x$

$\therefore g^{\prime}(x)=\frac{1}{x}$

क्योंकि $\log x$ धनात्मक संख्या $x$ के लिए परिभाषित है, $g^{\prime}(x)>0$ कोई भी $x$ के लिए होता है।

इसलिए, कोई भी $c \in \mathbf{R}$ ऐसा नहीं है जैसे कि $g^{\prime}(c)=0$.

इसलिए, फलन $g$ उच्चिष्ठ या निम्निष्ठ नहीं हो सकता।

iii. हम जानते हैं,

$h(x)=x^{3}+x^{2}+x+1$

$\therefore h^{\prime}(x)=3 x^{2}+2 x+1$

अब,

$h(x)=0 \Rightarrow 3 x^{2}+2 x+1=0 \Rightarrow x=\frac{-2 \pm 2 \sqrt{2} i}{6}=\frac{-1 \pm \sqrt{2} i}{3} \notin \mathbf{R}$

इसलिए, कोई भी $c \in \mathbf{R}$ ऐसा नहीं है जैसे कि $h^{\prime}(c)=0$.

इसलिए, फलन $h$ उच्चिष्ठ या निम्निष्ठ नहीं हो सकता।

Solution

(i) दी गई फलन $f(x)=x^{3}$ है।

$\therefore f^{\prime}(x)=3 x^{2}$

अब,

$f^{\prime}(x)=0 \Rightarrow x=0$

फिर, हम अंतिम बिंदुओं $[-2,2]$ पर फलन $f$ के मान का मूल्यांकन करते हैं।

$f(0)=0$

$f(-2)=(-2)^{3}=-8$

$f(2)=(2)^{3}=8$

इसलिए, हम निष्कर्ष निकाल सकते हैं कि फलन $f$ का अंतिम अधिकतम मान $[-2,2]$ पर 8 है जो $x=2$ पर होता है। इसके अलावा, फलन $f$ का अंतिम न्यूनतम मान $[-2,2]$ पर -8 है जो $x=-2$ पर होता है।

(ii) दी गई फलन $f(x)=\sin x+\cos x$ है।

$\therefore f^{\prime}(x)=\cos x-\sin x$

अब,

$f^{\prime}(x)=0 \Rightarrow \sin x=\cos x \Rightarrow \tan x=1 \Rightarrow x=\frac{\pi}{4}$

फिर, हम अंतिम बिंदुओं $[0, \pi]$ पर फलन $f$ के मान का मूल्यांकन करते हैं।

Solution

लाभ फलन निम्नलिखित द्वारा दिया गया है $p(x)=41-24 x-18 x^{2}$।

$\therefore p^{\prime}(x)=-24-36 x$

$p^{\prime \prime}(x)=-36$

अब,

$p^{\prime}(x)=0 \Rightarrow x=\frac{-24}{36}=-\frac{2}{3}$

इसके अलावा,

$p^{\prime \prime}(\frac{-2}{3})=-36<0$

द्वितीय अवकलज परीक्षण के अनुसार, $x=-\frac{2}{3}$ फलन $p$ के लोकल अधिकतम बिंदु है।

$\therefore$ अधिकतम लाभ $=p(-\frac{2}{3})$

$ \begin{aligned} & =41-24(-\frac{2}{3})-18(-\frac{2}{3})^{2} \\ & =41+16-8 \\ & =49 \end{aligned} $

इसलिए, कंपनी द्वारा किए जाने वाले अधिकतम लाभ 49 इकाई है।

Solution

$f(x)=3 x^4-8 x^3+12 x^2-48 x+25$

$f^{\prime}(x)=0$ के लिए अंतर बिंदुओं का खोज करें

$f^{\prime}(x)=12 x^3-24 x^2+24 x-48$

$12 x^3-24 x^2+24 x-48=0$

$12 x^2(x-2)+24(x-2)=0$

$\left(12 x^2+24\right)(x-2)=0$

क्योंकि $12 x^2+24 \neq 0$ और $x-2=0 \Longrightarrow x=2$

हमें $x=0,2,3$ पर जांच करनी होगी $f(0)=25$

$f(2)=-39$

$f(3)=16$

$\therefore$ $f(x)$ का अधिकतम मान $x=0$ पर 25 है

$f(x)$ का न्यूनतम मान $x=2$ पर -39 है

Solution

मान लीजिए $f(x)=\sin 2 x$.

$\therefore f^{\prime}(x)=2 \cos 2 x$

अब,

$ \begin{aligned} & f^{\prime}(x)=0 \Rightarrow \cos 2 x=0 \\ & \Rightarrow 2 x=\frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2}, \frac{7 \pi}{2} \\ & \Rightarrow x=\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4} \end{aligned} $

फिर, हम अंतराल $[0,2 \pi]$ के सीमा बिंदुओं $x=\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4}$ पर $f$ के मान का मूल्यांकन करते हैं।

$f(\frac{\pi}{4})=\sin \frac{\pi}{2}=1, f(\frac{3 \pi}{4})=\sin \frac{3 \pi}{2}=-1$

$f(\frac{5 \pi}{4})=\sin \frac{5 \pi}{2}=1, f(\frac{7 \pi}{4})=\sin \frac{7 \pi}{2}=-1$

$f(0)=\sin 0=0, f(2 \pi)=\sin 2 \pi=0$

इसलिए, हम निष्कर्ष निकाल सकते हैं कि $f$ का अंतराल $[0,2 \pi]$ पर अधिकतम मान निम्नलिखित बिंदुओं पर हो रहा है

$x=\frac{\pi}{4}$ और $x=\frac{5 \pi}{4}$ पर।

Solution

मान लीजिए $f(x)=\sin x+\cos x$.

$\therefore f^{\prime}(x)=\cos x-\sin x$

$f^{\prime}(x)=0 \Rightarrow \sin x=\cos x \Rightarrow \tan x=1 \Rightarrow x=\frac{\pi}{4}, \frac{5 \pi}{4} \ldots$,

$f^{\prime \prime}(x)=-\sin x-\cos x=-(\sin x+\cos x)$

अब, $f^{\prime \prime}(x)$ नकारात्मक होगा जब $(\sin x+\cos x)$ धनात्मक हो, अर्थात जब $\sin x$ और $\cos x$ दोनों धनात्मक हों। हम जानते हैं कि $\sin x$ और $\cos x$ दोनों पहले चतुर्थांश में धनात्मक होते हैं। तब, $f^{\prime \prime}(x)$ नकारात्मक होगा जब $x \in(0, \frac{\pi}{2})$।

इसलिए, हम $x=\frac{\pi}{4}$ को ध्यान में रखते हैं।

$f^{\prime \prime}(\frac{\pi}{4})=-(\sin \frac{\pi}{4}+\cos \frac{\pi}{4})=-(\frac{2}{\sqrt{2}})=-\sqrt{2}<0$ $\square$ द्वितीय अवकलज परीक्षण के अनुसार, $f$ का अधिकतम मान $x=\frac{\pi}{4}$ पर होगा और $f$ का अधिकतम मान $f(\frac{\pi}{4})=\sin \frac{\pi}{4}+\cos \frac{\pi}{4}=\frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}$ होगा।

हल

मान लीजिए $f(x)=2 x^{3}-24 x+107$।

$\therefore f^{\prime}(x)=6 x^{2}-24=6(x^{2}-4)$

अब,

$f^{\prime}(x)=0 \Rightarrow 6(x^{2}-4)=0 \Rightarrow x^{2}=4 \Rightarrow x= \pm 2$

हम पहले अंतराल $[1,3]$ को ध्यान में रखते हैं।

फिर, हम अंतराल $[1,3]$ के क्रिटिकल बिंदु $x=2 \square[1,3]$ और अंतराल $[1,3]$ के सीमा बिंदुओं पर $f$ के मान का मूल्यांकन करते हैं।

$f(2)=2(8)-24(2)+107=16-48+107=75$

$f(1)=2(1)-24(1)+107=2-24+107=85$

$f(3)=2(27)-24(3)+107=54-72+107=89$

इसलिए, अंतराल $[1,3]$ में $f(x)$ का अंतराल अधिकतम मान 89 है जो $x=3$ पर होता है।

अब, हम अंतराल $[-3,-1]$ को ध्यान में रखते हैं।

अंतराल $[-3,-1]$ के क्रिटिकल बिंदु $x=-2 \square[-3,-1]$ और अंतराल $[1,3]$ के सीमा बिंदुओं पर $f$ के मान का मूल्यांकन करते हैं।

$f(-3)=2(-27)-24(-3)+107=-54+72+107=125$

$f(-1)=2(-1)-24(-1)+107=-2+24+107=129$

$f(-2)=2(-8)-24(-2)+107=-16+48+107=139$

इसलिए, अंतराल $[-3,-1]$ में $f(x)$ का अंतराल अधिकतम मान 139 है जो $x=-2$ पर होता है।

हल

मान लीजिए $f(x)=x^{4}-62 x^{2}+a x+9$।

$\therefore f^{\prime}(x)=4 x^{3}-124 x+a$

यह दिया गया है कि फलन $f$ अंतराल $[0,2]$ में $x=1$ पर अपना अधिकतम मान प्राप्त करता है।

$\therefore f^{\prime}(1)=0$

$\Rightarrow 4-124+a=0$

$\Rightarrow a=120$

इसलिए, $a$ का मान 120 है।

हल

मान लीजिए $f(x)=x+\sin 2 x$।

$\therefore f^{\prime}(x)=1+2 \cos 2 x$

अब, $f^{\prime}(x)=0 \Rightarrow \cos 2 x=-\frac{1}{2}=-\cos \frac{\pi}{3}=\cos (\pi-\frac{\pi}{3})=\cos \frac{2 \pi}{3}$

$2 x=2 \pi \pm \frac{2 \pi}{3} \quad n \in \mathbf{Z}$

$\Rightarrow x=n \pi \pm \frac{\pi}{3}, n \in \mathbf{Z}$

$\Rightarrow x=\frac{\pi}{3}, \frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{5 \pi}{3} \in[0,2 \pi]$

तब, हम अंतराल $[0,2 \pi]$ के क्रिटिकल बिंदुओं $x=\frac{\pi}{3}, \frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{5 \pi}{3}$ और अंतराल के सीमा बिंदुओं $[0,2 \pi]$ पर $f$ के मान का मूल्यांकन करते हैं। $f(\frac{\pi}{3})=\frac{\pi}{3}+\sin \frac{2 \pi}{3}=\frac{\pi}{3}+\frac{\sqrt{3}}{2}$

$f(\frac{2 \pi}{3})=\frac{2 \pi}{3}+\sin \frac{4 \pi}{3}=\frac{2 \pi}{3}-\frac{\sqrt{3}}{2}$

$f(\frac{4 \pi}{3})=\frac{4 \pi}{3}+\sin \frac{8 \pi}{3}=\frac{4 \pi}{3}+\frac{\sqrt{3}}{2}$

$f(\frac{5 \pi}{3})=\frac{5 \pi}{3}+\sin \frac{10 \pi}{3}=\frac{5 \pi}{3}-\frac{\sqrt{3}}{2}$

$f(0)=0+\sin 0=0$

$f(2 \pi)=2 \pi+\sin 4 \pi=2 \pi+0=2 \pi$

इसलिए, हम निष्कर्ष निकाल सकते हैं कि अंतराल $[0,2 \pi]$ में $f(x)$ का अंतराल अधिकतम मान $2 \pi$ है जो $x=2 \pi$ पर होता है और अंतराल का अंतराल न्यूनतम मान 0 है जो $x=0$ पर होता है।

हल

मान लीजिए एक संख्या $x$ है। तब, दूसरी संख्या $(24-x)$ होती है।

मान लीजिए $P(x)$ दोनों संख्याओं के गुणनफल को दर्शाता है। इसलिए, हम निम्नलिखित रखते हैं:

$ \begin{aligned} & P(x)=x(24-x)=24 x-x^{2} \\ & \therefore P^{\prime}(x)=24-2 x \\ & P^{\prime \prime}(x)=-2 \end{aligned} $

अब,

$P^{\prime}(x)=0 \Rightarrow x=12$

इसके अतिरिक्त,

$P^{\prime \prime}(12)=-2<0$

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, $x=12$ $P$ के लोकल मैक्सिमा के बिंदु है। इसलिए, जब संख्याएं 12 और $24-12=12$ होती हैं तब उत्पाद अधिकतम होता है।

हल

दो संख्याएं $x$ और $y$ जैसे कि $x+y=60$ हैं।

$\square y=60-x$

मान लीजिए $f(x)=x y^{3}$.

$\Rightarrow f(x)=x(60-x)^{3}$

$\therefore f^{\prime}(x)=(60-x)^{3}-3 x(60-x)^{2}$

$=(60-x)^{2}[60-x-3 x]$

$=(60-x)^{2}(60-4 x)$

और, $f^{\prime \prime}(x)=-2(60-x)(60-4 x)-4(60-x)^{2}$

$ \begin{aligned} & =-2(60-x)[60-4 x+2(60-x)] \\ & =-2(60-x)(180-6 x) \\ & =-12(60-x)(30-x) \end{aligned} $

अब, $f^{\prime}(x)=0 \Rightarrow x=60$ या $x=15$

जब $x=60, f^{\prime \prime}(x)=0$ है।

जब $x=15, f^{\prime \prime}(x)=-12(60-15)(30-15)=-12 \times 45 \times 15<0$ है।

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, $x=15$ फलन $f$ के एक लोकल मैक्सिमा बिंदु है। अतः, फलन $x y^{3}$ का मान $x=15$ और $y=60-15=45$ के लिए अधिकतम होता है।

अतः, आवश्यक संख्याएँ 15 और 45 हैं।

हल

मान लीजिए एक संख्या $x$ है। तब, दूसरी संख्या $y=(35-x)$ है।

मान लीजिए $P(x)=x^{2} y^{5}$. तब, हमारे पास है:

$ \begin{aligned} & P(x)=x^{2}(35-x)^{5} \\ & \begin{aligned} \therefore P^{\prime}(x) & =2 x(35-x)^{5}-5 x^{2}(35-x)^{4} \\ & =x(35-x)^{4}[2(35-x)-5 x] \\ & =x(35-x)^{4}(70-7 x) \\ & =7 x(35-x)^{4}(10-x) \end{aligned} \end{aligned} $

और, $P^{\prime \prime}(x)=7(35-x)^{4}(10-x)+7 x[-(35-x)^{4}-4(35-x)^{3}(10-x)]$

$ \begin{aligned} & =7(35-x)^{4}(10-x)-7 x(35-x)^{4}-28 x(35-x)^{3}(10-x) \\ & =7(35-x)^{3}[(35-x)(10-x)-x(35-x)-4 x(10-x)] \\ & =7(35-x)^{3}[350-45 x+x^{2}-35 x+x^{2}-40 x+4 x^{2}] \\ & =7(35-x)^{3}(6 x^{2}-120 x+350) \end{aligned} $

अब, $P^{\prime}(x)=0 \Rightarrow x=0, x=35, x=10$

जब $x=35, P^{\prime}(x)=f(x)=0$ और $y=35-35=0$ है। यह उत्पाद $x^{2} y^{5}$ को शून्य बनाएगा।

जब $x=0, y=35-0=35$ और उत्पाद $x^{2} y^{5}$ शून्य होगा।

$\square x=0$ और $x=35$ के संभावित मान नहीं हो सकते।

जब $x=10$, हमारे पास है:

$ \begin{aligned} P^{\prime \prime}(x) & =7(35-10)^{3}(6 \times 100-120 \times 10+350) \\ & =7(25)^{3}(-250)<0 \end{aligned} $

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, $P(x)$ का मान $x=10$ और $y=35-10=25$ के लिए अधिकतम होता है।

अतः, आवश्यक संख्याएँ 10 और 25 हैं।

हल

मान लीजिए एक संख्या $x$ है। तब, दूसरी संख्या $(16-x)$ होगी।

इन संख्याओं के घनों के योग को $S(x)$ से नोट करते हैं। तब,

$S(x)=x^{3}+(16-x)^{3}$

$\therefore S^{\prime}(x)=3 x^{2}-3(16-x)^{2}, S^{\prime \prime}(x)=6 x+6(16-x)$

अब, $S^{\prime}(x)=0 \Rightarrow 3 x^{2}-3(16-x)^{2}=0$

$\Rightarrow x^{2}-(16-x)^{2}=0$

$\Rightarrow x^{2}-256-x^{2}+32 x=0$

$\Rightarrow x=\frac{256}{32}=8$

अब, $S^{\prime \prime}(8)=6(8)+6(16-8)=48+48=96>0$

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, $x=8$ $S$ के लोकल मिनिमा बिंदु है।

इसलिए, संख्याओं के घनों का योग जब संख्याएँ 8 और $16-8=8$ होती हैं तब न्यूनतम होता है।

हल

मान लीजिए काटे गए वर्ग की भुजा $x$ सेमी है। तब, बॉक्स की लंबाई और चौड़ाई $(18-2 x)$ सेमी होगी और बॉक्स की ऊंचाई $x$ सेमी होगी।

इसलिए, बॉक्स का आयतन $V(x)$ निम्नलिखित द्वारा दिया जाता है,

$V(x)=x(18-2 x)^{2}$ $\therefore V^{\prime}(x)=(18-2 x)^{2}-4 x(18-2 x)$

$=(18-2 x)[18-2 x-4 x]$

$=(18-2 x)(18-6 x)$

$=6 \times 2(9-x)(3-x)$

$=12(9-x)(3-x)$

और, $V^{\prime \prime}(x)=12[-(9-x)-(3-x)]$

$=-12(9-x+3-x)$

$=-12(12-2 x)$

$=-24(6-x)$

अब, $V^{\prime}(x)=0 \Rightarrow x=9$ या $x=3$

यदि $x=9$, तो लंबाई और चौड़ाई शून्य हो जाएगी।

$\therefore x \neq 9$.

$\Rightarrow x=3$.

अब, $V^{\prime \prime}(3)=-24(6-3)=-72<0$

$\therefore$ द्वितीय अवकलज परीक्षण के अनुसार, $x=3$ $V$ के अधिकतम बिंदु है।

इसलिए, यदि हम वर्ग टिन के प्रत्येक कोने से 3 सेमी भुजा वाला वर्ग काट दें और बचे हुए शीट से बॉक्स बनाएं, तो प्राप्त बॉक्स का आयतन अधिकतम होगा।

हल

मान लीजिए वर्ग के काटे गए किनारे की लंबाई $x cm$ है। तब, बॉक्स की ऊंचाई $x$, लंबाई $45-2 x$ और चौड़ाई $24-2 x$ है।

इसलिए, बॉक्स का आयतन $V(x)$ निम्नलिखित द्वारा दिया जाता है,

$ \begin{aligned} V(x) & =x(45-2 x)(24-2 x) \\ & =x(1080-90 x-48 x+4 x^{2}) \\ & =4 x^{3}-138 x^{2}+1080 x \end{aligned} $

$\therefore V^{\prime}(x)=12 x^{2}-276 x+1080$

$ =12(x^{2}-23 x+90) $

$ =12(x-18)(x-5) $

$V^{\prime \prime}(x)=24 x-276=12(2 x-23)$

अब, ${ }^{V^{\prime}}(x)=0 \Rightarrow x=18$ और $x=5$

एक आयताकार शीट के प्रत्येक कोने से $18 cm$ के वर्ग काटना संभव नहीं है। इसलिए, $x$ 18 के बराबर नहीं हो सकता।

$\square x=5$

अब, $V^{\prime \prime}(5)=12(10-23)=12(-13)=-156<0$

$\therefore$ द्वितीय अवकलज परीक्षण के अनुसार, $x=5$ अधिकतम बिंदु है।

इसलिए, बॉक्स के आयतन को अधिकतम करने के लिए काटे गए वर्ग के किनारे की लंबाई $5 cm$ है।

हल

मान लीजिए एक आयत जिसकी लंबाई $l$ और चौड़ाई $b$ है, दिए गए वृत्त में आकर्षित है जिसकी त्रिज्या $a$ है। तब, विकर्ण केंद्र से गुजरता है और इसकी लंबाई $2 a cm$ है।

अब, पिथागोरस प्रमेय के द्वारा हम निम्नलिखित प्राप्त करते हैं:

$ \begin{aligned} & (2 a)^{2}=l^{2}+b^{2} \\ & \Rightarrow b^{2}=4 a^{2}-l^{2} \\ & \Rightarrow b=\sqrt{4 a^{2}-l^{2}} \end{aligned} $

$\square$ आयत का क्षेत्रफल, $A=l \sqrt{4 a^{2}-l^{2}}$

$\therefore \frac{d A}{d l}=\sqrt{4 a^{2}-l^{2}}+l \frac{1}{2 \sqrt{4 a^{2}-l^{2}}}(-2 l)=\sqrt{4 a^{2}-l^{2}}-\frac{l^{2}}{\sqrt{4 a^{2}-l^{2}}}$

$ =\frac{4 a^{2}-2 l^{2}}{\sqrt{4 a^{2}-l^{2}}} `

$

$\frac{d^{2} A}{d l^{2}}=\frac{\sqrt{4 a^{2}-l^{2}}(-4 l)-(4 a^{2}-2 l^{2}) \frac{(-2 l)}{2 \sqrt{4 a^{2}-l^{2}}}}{(4 a^{2}-l^{2})}$

$ =\frac{(4 a^{2}-l^{2})(-4 l)+l(4 a^{2}-2 l^{2})}{(4 a^{2}-l^{2})^{\frac{3}{2}}} $

$ =\frac{-12 a^{2} l+2 l^{3}}{(4 a^{2}-l^{2})^{\frac{3}{2}}}=\frac{-2 l(6 a^{2}-l^{2})}{(4 a^{2}-l^{2})^{\frac{3}{2}}} $

अब, $\frac{d A}{d l}=0$ देता है $4 a^{2}=2 l^{2} \Rightarrow l=\sqrt{2} a$

$ \Rightarrow b=\sqrt{4 a^{2}-2 a^{2}}=\sqrt{2 a^{2}}=\sqrt{2} a $

अब, जब $l=\sqrt{2} a$,

$\frac{d^{2} A}{d l^{2}}=\frac{-2(\sqrt{2} a)(6 a^{2}-2 a^{2})}{2 \sqrt{2} a^{3}}=\frac{-8 \sqrt{2} a^{3}}{2 \sqrt{2} a^{3}}=-4<0$

$\therefore$ द्वितीय अवकलज परीक्षण के अनुसार, जब $l=\sqrt{2} a$, तो आयत का क्षेत्रफल अधिकतम होता है।

क्योंकि $l=b=\sqrt{2} a$, तो आयत एक वर्ग होता है।

इसलिए, साबित कर दिया गया है कि दिए गए निश्चित वृत्त में आयत के सभी आकृतियों में वर्ग का क्षेत्रफल अधिकतम होता है।

हल

मान लीजिए $r$ और $h$ बेलन की त्रिज्या और ऊंचाई हैं।

तब, बेलन के सतह क्षेत्रफल $(S)$ द्वारा दिया गया है,

$ \begin{aligned} & S=2 \pi r^{2}+2 \pi r h \\ & \Rightarrow h=\frac{S-2 \pi r^{2}}{2 \pi r} \\ &=\frac{S}{2 \pi}(\frac{1}{r})-r \end{aligned} $

मान लीजिए $V$ बेलन का आयतन है। तब,

$V=\pi r^{2} h=\pi r^{2}[\frac{S}{2 \pi}(\frac{1}{r})-r]=\frac{S r}{2}-\pi r^{3}$

तब, $\frac{d V}{d r}=\frac{S}{2}-3 \pi r^{2}, \frac{d^{2} V}{d r^{2}}=-6 \pi r$

अब, $\frac{d V}{d r}=0 \Rightarrow \frac{S}{2}=3 \pi r^{2} \Rightarrow r^{2}=\frac{S}{6 \pi}$

जब $r^{2}=\frac{S}{6 \pi}$, तब $\frac{d^{2} V}{d r^{2}}=-6 \pi(\sqrt{\frac{S}{6 \pi}})<0$।

द्वितीय अवकलज परीक्षण के अनुसार, जब $r^{2}=\frac{S}{6 \pi}$, तो आयतन अधिकतम होता है।

अब, जब $r^{2}=\frac{S}{6 \pi}$, तब $h=\frac{6 \pi r^{2}}{2 \pi}(\frac{1}{r})-r=3 r-r=2 r$।

इसलिए, आयतन तब अधिकतम होता है जब ऊंचाई त्रिज्या के दुगुनी हो, अर्थात जब ऊंचाई व्यास के बराबर हो।

हल

मान लीजिए $r$ और $h$ क्रमशः बेलन की त्रिज्या और ऊंचाई है।

तब, बेलन का आयतन $(V)$ निम्नलिखित है,

$V=\pi r^{2} h=100 \quad$ (दिया गया)

$\therefore h=\frac{100}{\pi r^{2}}$

बेलन के सतह क्षेत्रफल $(S$ ) निम्नलिखित है,

$S=2 \pi r^{2}+2 \pi r h=2 \pi r^{2}+\frac{200}{r}$

$\therefore \frac{d S}{d r}=4 \pi r-\frac{200}{r^{2}}, \frac{d^{2} S}{d r^{2}}=4 \pi+\frac{400}{r^{3}}$

$\frac{d S}{d r}=0 \Rightarrow 4 \pi r=\frac{200}{r^{2}}$

$\Rightarrow r^{3}=\frac{200}{4 \pi}=\frac{50}{\pi}$

$\Rightarrow r=(\frac{50}{\pi})^{\frac{1}{3}}$

अब, यह देखा जाता है कि जब $r=(\frac{50}{\pi})^{\frac{1}{3}}, \frac{d^{2} S}{d r^{2}}>0$ है।

$\square$ द्वितीय अवकलज परीक्षण द्वारा, सतह क्षेत्रफल न्यूनतम होता है जब बेलन की त्रिज्या $(\frac{50}{\pi})^{\frac{1}{3}} cm$ हो।

जब $r=(\frac{50}{\pi})^{\frac{1}{3}}, h=\frac{100}{\pi(\frac{50}{\pi})^{\frac{2}{3}}}=\frac{2 \times 50}{(50)^{\frac{2}{3}}()^{1-\frac{2}{3}}}=2(\frac{50}{\pi})^{\frac{1}{3}} cm$ होता है।

इसलिए, न्यूनतम सतह क्षेत्रफल वाली टंकी की आवश्यक विमाएं त्रिज्या $=(\frac{50}{\pi})^{\frac{1}{3}} cm$ और ऊंचाई $=2(\frac{50}{\pi})^{\frac{1}{3}} cm$ है।

हल

मान लीजिए दिए गए तार से एक टुकड़े की लंबाई $l$ हो।

तब, वृत्त के रूप में बनाने के लिए दूसरे टुकड़े की लंबाई $(28 - l) m$ होती है।

अब, वर्ग की भुजा $=\frac{l}{4}$।

$ r $ के वृत्त की त्रिज्या होने दें। तब,

$ 2 \pi r=28-l \Rightarrow r=\frac{1}{2 \pi}(28-l) \text{. } $

वर्ग और वृत्त के संयुक्त क्षेत्रफल $(A)$ निम्नलिखित द्वारा दिया जाता है,

$A=(\text{ वर्ग की भुजा })^{2}+r^{2}$

$=\frac{l^{2}}{16}+\pi[\frac{1}{2 \pi}(28-l)]^{2}$

$=\frac{l^{2}}{16}+\frac{1}{4 \pi}(28-l)^{2}$

$\therefore \frac{d A}{d l}=\frac{2 l}{16}+\frac{2}{4 \pi}(28-l)(-1)=\frac{l}{8}-\frac{1}{2 \pi}(28-l)$

$\frac{d^{2} A}{d l^{2}}=\frac{1}{8}+\frac{1}{2 \pi}>0$

अब, $\frac{d A}{d l}=0 \Rightarrow \frac{l}{8}-\frac{1}{2 \pi}(28-l)=0$

$\Rightarrow \frac{\pi l-4(28-l)}{8 \pi}=0$

$\Rightarrow(\pi+4) l-112=0$

$\Rightarrow l=\frac{112}{\pi+4}$

इसलिए, जब $l=\frac{112}{\pi+4}, \frac{d^{2} A}{d l^{2}}>0$ होता है।

$\therefore$ द्वितीय अवकलज परीक्षण के अनुसार, क्षेत्रफल $(A)$ जब $l=\frac{112}{\pi+4}$ होता है, तब न्यूनतम होता है।

इसलिए, जब वर्ग के निर्माण के तार की लंबाई $\frac{112}{\pi+4} cm$ होती है, तब संयुक्त क्षेत्रफल न्यूनतम होता है। वृत्त के निर्माण के तार की लंबाई $28-\frac{112}{\pi+4}=\frac{28 \pi}{\pi+4} cm$ होती है।

हल

मान लीजिए $r$ और $h$ क्रमशः एक गोले के त्रिज्या $R$ के अंतर्गत अंतर्विष्ट शंकु की त्रिज्या और ऊँचाई हो।

मान लीजिए $V$ शंकु का आयतन हो।

तब, $V=\frac{1}{3} \pi r^{2} h$

शंकु की ऊँचाई निम्नलिखित द्वारा दी जाती है,

$h=R+AB=R+\sqrt{R^{2}-r^{2}} \quad$ [ $ABC$ एक समकोण त्रिकोण है]

$ \begin{aligned} & \therefore V=\frac{1}{3} \pi r^{2}(R+\sqrt{R^{2}-r^{2}}) \\ & =\frac{1}{3} \pi r^{2} R+\frac{1}{3} \pi r^{2} \sqrt{R^{2}-r^{2}} \\ & \therefore \frac{d V}{d r}=\frac{2}{3} \pi r R+\frac{2}{3} \pi r \sqrt{R^{2}-r^{2}}+\frac{1}{3} \pi r^{2} \cdot \frac{(-2 r)}{2 \sqrt{R^{2}-r^{2}}} \\

$$ \begin{aligned} & =\frac{2}{3} \pi r R+\frac{2}{3} \pi r \sqrt{R^{2}-r^{2}}-\frac{1}{3} \pi \frac{r^{3}}{\sqrt{R^{2}-r^{2}}} \\ & =\frac{2}{3} \pi r R+\frac{2 \pi r(R^{2}-r^{2})-\pi r^{3}}{3 \sqrt{R^{2}-r^{2}}} \\ & =\frac{2}{3} \pi r R+\frac{2 \pi r R^{2}-3 \pi r^{3}}{3 \sqrt{R^{2}-r^{2}}} \\ & \frac{d^{2} V}{d r^{2}}=\frac{2 \pi R}{3}+\frac{3 \sqrt{R^{2}-r^{2}}(2 \pi R^{2}-9 \pi r^{2})-(2 \pi r R^{2}-3 \pi r^{3}) \cdot \frac{(-2 r)}{6 \sqrt{R^{2}-r^{2}}}}{9(R^{2}-r^{2})} \\ & =\frac{2}{3} \pi R+\frac{9(R^{2}-r^{2})(2 \pi R^{2}-9 \pi r^{2})+2 \pi r^{2} R^{2}+3 \pi r^{4}}{27(R^{2}-r^{2})^{\frac{3}{2}}} \end{aligned} $$

अब, $\frac{d V}{d r}=0 \Rightarrow \frac{2}{3} \quad r R=\frac{3 \pi r^{3}-2 \pi r R^{2}}{3 \sqrt{R^{2}-r^{2}}}$

$\Rightarrow 2 R=\frac{3 r^{2}-2 R^{2}}{\sqrt{R^{2}-r^{2}}} \Rightarrow 2 R \sqrt{R^{2}-r^{2}}=3 r^{2}-2 R^{2}$

$\Rightarrow 4 R^{2}(R^{2}-r^{2})=(3 r^{2}-2 R^{2})^{2}$

$\Rightarrow 4 R^{4}-4 R^{2} r^{2}=9 r^{4}+4 R^{4}-12 r^{2} R^{2}$

$\Rightarrow 9 r^{4}=8 R^{2} r^{2}$

$\Rightarrow r^{2}=\frac{8}{9} R^{2}$

जब $r^{2}=\frac{8}{9} R^{2}$, तो $\frac{d^{2} V}{d r^{2}}<0$।

द्वितीय अवकलज परीक्षण के अनुसार, शंकु का आयतन जब $r^{2}=\frac{8}{9} R^{2}$ होता है, तब अधिकतम होता है।

जब $r^{2}=\frac{8}{9} R^{2}, h=R+\sqrt{R^{2}-\frac{8}{9} R^{2}}=R+\sqrt{\frac{1}{9} R^{2}}=R+\frac{R}{3}=\frac{4}{3} R$।

इसलिए,

$=\frac{1}{3} \pi(\frac{8}{9} R^{2})(\frac{4}{3} R)$

$=\frac{8}{27}(\frac{4}{3} \pi R^{3})$

$=\frac{8}{27} \times($ गोले का आयतन $)$

इसलिए, गोले में अंकित सबसे बड़े शंकु का आयतन गोले के आयतन के $\frac{8}{27}$ होता है।

हल

मान लीजिए $r$ और $h$ क्रमशः शंकु की त्रिज्या और ऊँचाई (ऊंचाई) है।

तब, शंकु का आयतन $(V)$ निम्नलिखित द्वारा दिया गया है:

$V=\frac{1}{3} \pi r^{2} h \Rightarrow h=\frac{3 V}{r^{2}}$

अपकेंद्री शंकु के सतह क्षेत्रफल $(S)$ द्वारा दिया जाता है,

$S=\pi r l$ (जहाँ $/$ झुकाव ऊंचाई है)

$=\pi r \sqrt{r^{2}+h^{2}}$

$=\pi r \sqrt{r^{2}+\frac{9 \hbar^{2}}{\pi^{2} r^{4}}} \stackrel{\pi}{=} \frac{r \sqrt{9^{2} r^{6}+V^{2}}}{\pi r^{2}}$

$=\frac{1}{r} \sqrt{\pi^{3} r^{6}+9 V^{2}}$

$ \begin{aligned} \therefore \frac{d S}{d r} & =\frac{r \cdot \frac{6 \pi^{2} r^{5}}{2 \sqrt{{ }^{2} r^{6} 9 V^{2}}}-\sqrt{\pi^{2} r^{6}+9 V^{2}}}{r^{2}} \\ & =\frac{3 \pi^{2} r^{6}-\pi^{2} r^{6}-9 V^{2}}{r^{2} \sqrt{\pi^{2} r^{6}+9 V^{2}}} \\ & =\frac{2 \pi^{2} r^{6}-9 V^{2}}{r^{2} \sqrt{\pi^{2} r^{6}+9 V^{2}}} \\ & =\frac{2 \pi^{2} r^{6}-9 V^{2}}{r^{2} \sqrt{\pi^{2} r^{6}+9 V^{2}}} \end{aligned} $

अब, $\frac{d S}{d r}=0 \Rightarrow 2 \pi^{2} r^{6}=9 V^{2} \Rightarrow r^{6}=\frac{9 V^{2}}{2 \pi^{2}}$

इसलिए, यह आसानी से जांचा जा सकता है कि जब $r^{6}=\frac{9 V^{2}}{2 \pi^{2}}, \frac{d^{2} S}{d r^{2}}>0$ होता है।

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, शंकु के सतह क्षेत्रफल न्यूनतम होता है जब $r^{6}=\frac{9 V^{2}}{2 \pi^{2}}$ हो।

जब $r^{6}=\frac{9 V^{2}}{2 \pi^{2}}, h=\frac{3 V}{\pi r^{2}}=\frac{3}{\pi r^{2}}(\frac{2 \pi^{2} r^{6}}{9})^{\frac{1}{2}}=\frac{3}{\pi r^{2}} \cdot \frac{\sqrt{2} \pi r^{3}}{3}=\sqrt{2} r$।

इसलिए, दिए गए आयतन के लिए, न्यूनतम वक्र सतह वाले सम वृत्तीय शंकु की ऊंचाई आधार की त्रिज्या के $\sqrt{2}$ गुना होती है।

हल

मान लीजिए $\theta$ शंकु का अर्ध-शीर्ष कोण है।

स्पष्ट रूप से,

$ \theta \in[0, \frac{\pi}{2}] $

मान लीजिए $r, h$, और $/$ क्रमशः शंकु की त्रिज्या, ऊंचाई और झुकाव ऊंचाई है। शंकु की झुकाव ऊंचाई निर्धारित की गई है।

अब, $r=I \sin \theta$ और $h=I \cos \theta$

शंकु का आयतन $(V)$ निम्नलिखित द्वारा दिया जाता है,

$ \begin{aligned} & V=\frac{1}{3} \pi r^{2} h \\ & =\frac{1}{3} \pi(l^{2} \sin ^{2} \theta)(l \cos \theta) \\ & =\frac{1}{3} \pi l^{3} \sin ^{2} \theta \cos \theta \\ & \begin{aligned} \therefore \frac{d V}{d \theta} & =\frac{l^{3} \pi}{3}[\sin ^{2} \theta(-\sin \theta)+\cos \theta(2 \sin \theta \cos \theta)] \\ & =\frac{l^{3} \pi}{3}[-\sin ^{3}+2 \sin \theta \cos ^{2} \theta] \end{aligned} \\ & \begin{aligned} \frac{d^{2} V}{d \theta^{2}} & =\frac{l^{3} \pi}{3}[-3 \sin ^{2} \theta \cos \theta+2 \cos ^{3} \theta-4 \sin ^{2} \theta \cos \theta] \\ & =\frac{l^{3} \pi}{3}[2 \cos ^{3} \theta-7 \sin ^{2} \theta \cos \theta] \end{aligned} \end{aligned} $

अब, $\frac{d V}{d \theta}=0$

$\Rightarrow \sin ^{3} \theta=2 \sin \theta \cos ^{2} \theta$

$\Rightarrow \tan ^{2} \theta=2$

$\Rightarrow \tan \theta=\sqrt{2}$

$\Rightarrow \theta=\tan ^{-1} \sqrt{2}$

अब, जब $\theta=\tan ^{-1} \sqrt{2}$, तो $\tan ^{2} \theta=2$ या $\sin ^{2} \theta=2 \cos ^{2} \theta$।

तब, हम निम्नलिखित प्राप्त करते हैं:

$\frac{d^{2} V}{d \theta^{2}}=\frac{l^{3} \pi}{3}[2 \cos ^{3} \theta-14 \cos ^{3} \theta]=-4 \pi l^{3} \cos ^{3} \theta<0$ जब $\theta \in[0, \frac{\pi}{2}]$

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, आयतन $(V)$ अधिकतम होता है जब $\theta=\tan ^{-1} \sqrt{2}$।

इसलिए, दिए गए झुकाव ऊँचाई के लिए, अधिकतम आयतन वाले शंकु के अर्ध-शीर्षकोण $\tan ^{-1} \sqrt{2}$ होता है।

हल

मान लीजिए $\mathrm{r}, \mathrm{h}, \mathrm{l}$ क्रमशः एक सम वृत्तीय शंकु की त्रिज्या, ऊँचाई और झुकाव ऊँचाई हो। मान लीजिए $S$ शंकु के दिए गए सतह क्षेत्रफल हो। हम जानते हैं, $l^2=\mathrm{r}^2+\mathrm{h}^2 \ldots .(1)$

$\begin{aligned} & S=\pi r l+\pi r^2 \ & S-\pi r^2=\pi r l \ & \Rightarrow l=\frac{S-\pi r^2}{\pi r} \ldots . . \end{aligned}$

$\begin{aligned} & \mathrm{V}=\frac{1}{3} \pi \mathrm{r}^2 \mathrm{~h} \\ & \Rightarrow \mathrm{V}=\frac{1}{3} \pi \mathrm{r}^2 \sqrt{1^2-\mathrm{r}^2}(\mathrm{by}(1)) \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9} \pi^2 \mathrm{r}^4\left(\mathrm{l}^2-\mathrm{r}^2\right) \end{aligned}$

$\begin{aligned} & \Rightarrow \mathrm{V}^2=\frac{1}{9} \pi^2 \mathrm{r}^4\left[\left(\frac{\mathrm{S}-\pi \mathrm{r}^2}{\pi \mathrm{r}}\right)^2-\mathrm{r}^2\right] \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9} \pi^2 \mathrm{r}^4\left[\frac{\left(\mathrm{S}-\pi \mathrm{r}^2\right)^2-\pi^2 \mathrm{r}^4}{\pi^2 \mathrm{r}^2}\right] \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9} \mathrm{r}^2\left[\left(\mathrm{~S}-\pi \mathrm{r}^2\right)^2-\pi^2 \mathrm{r}^4\right] \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9} \mathrm{r}^2\left[\mathrm{~S}^2-2 \pi \mathrm{Sr}^2+\pi^2 \mathrm{r}^4-\pi^2 \mathrm{r}^4\right] \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9}\left(\mathrm{r}^2 \mathrm{~S}^2-2 \pi \mathrm{Sr}^4\right) \\ \end{aligned}$

$2 \mathrm{~V} \frac{\mathrm{dV}}{\mathrm{dr}}=\frac{\mathrm{S}^2}{9} 2 \mathrm{r}-\frac{2 \pi \mathrm{S}}{9} 4 \mathrm{r}^3$

$2 \mathrm{~V} \frac{\mathrm{dV}}{\mathrm{dr}}=\frac{2 \mathrm{rS}}{9}\left(\mathrm{~S}-4 \pi \mathrm{r}^2\right)$

अधिकतम आयतन के लिए, $\frac{\mathrm{dV}}{\mathrm{dr}}=0$

$\begin{aligned} & \Rightarrow \frac{2 \mathrm{rS}}{9}\left(\mathrm{~S}-4 \pi \mathrm{r}^2\right)=0 \\ & \Rightarrow \mathrm{r}=\mathrm{o} \text { or } \mathrm{S}-4 \pi \mathrm{r}^2=0 \end{aligned}$

क्योंकि, $r$ शून्य नहीं हो सकता

$\begin{aligned} & \Rightarrow \mathrm{S}=4 \pi \mathrm{r}^2 \ & \Rightarrow \mathrm{r}^2=\frac{\mathrm{S}}{4 \pi} \ & \Rightarrow \mathrm{r}^2=\frac{\pi \mathrm{rl}+\pi \mathrm{r}^2}{4 \pi} \end{aligned}$

$\begin{aligned} & \Rightarrow 4 \pi r^2=\pi r l+\pi r^2 \ & \Rightarrow 3 \pi r^2=\pi r l \ & \Rightarrow l=3 r \end{aligned}$

मान लीजिए $\alpha$ अर्ध-शीर्षकोण है।

$\begin{aligned} & \sin \alpha=\frac{r}{l} \\ & \sin \alpha=\frac{r}{3 r} \\ & \Rightarrow \alpha=\sin ^{-1}\left(\frac{1}{3}\right)

\end{aligned}$

हल

दिया गया वक्र $x^{2}=2 y$ है।

प्रत्येक $x$ के मान के लिए बिंदु की स्थिति $(x, \frac{x^{2}}{2})$ होगी।

बिंदु $(x, \frac{x^{2}}{2})$ और $(0,5)$ के बीच दूरी $d(x)$ निम्नलिखित द्वारा दी गई है,

$d(x)=\sqrt{(x-0)^{2}+(\frac{x^{2}}{2}-5)^{2}}=\sqrt{x^{2}+\frac{x^{4}}{4}+25-5 x^{2}}=\sqrt{\frac{x^{4}}{4}-4 x^{2}+25}$

$\therefore d^{\prime}(x)=\frac{(x^{3}-8 x)}{2 \sqrt{\frac{x^{4}}{4}-4 x^{2}+25}}=\frac{(x^{3}-8 x)}{\sqrt{x^{4}-16 x^{2}+100}}$

अब, $d^{\prime}(x)=0 \Rightarrow x^{3}-8 x=0$

$\Rightarrow x(x^{2}-8)=0$

$\Rightarrow x=0, \pm 2 \sqrt{2}$

$ \begin{aligned} & \begin{aligned} & \text{ और, } d^{\prime \prime}(x)= \frac{\sqrt{x^{4}-16 x^{2}+100}(3 x^{2}-8)-(x^{3}-8 x) \cdot \frac{4 x^{3}-32 x}{2 \sqrt{x^{4}-16 x^{2}+100}}}{(x^{4}-16 x^{2}+100)} \\ &=\frac{(x^{4}-16 x^{2}+100)(3 x^{2}-8)-2(x^{3}-8 x)(x^{3}-8 x)}{(x^{4}-16 x^{2}+100)^{\frac{3}{2}}} \\ &=\frac{(x^{4}-16 x^{2}+100)(3 x^{2}-8)-2(x^{3}-8 x)^{2}}{(x^{4}-16 x^{2}+100)^{\frac{3}{2}}} \\ & \text{ जब, } x=0 \text{, तो } d^{\prime \prime}(x)=\frac{36(-8)}{6^{3}}<0 . \end{aligned} \\ & \text{ जब, } x= \pm 2 \sqrt{2}, d^{\prime \prime}(x)>0 . \end{aligned} $

$\square$ दूसरे अवकलज परीक्षण द्वारा, $d(x)$ का मान $x= \pm 2 \sqrt{2}$ पर न्यूनतम होता है।

जब $x= \pm 2 \sqrt{2}, y=\frac{(2 \sqrt{2})^{2}}{2}=4$ होता है।

अतः, वक्र $x^{2}=2 y$ पर बिंदु $(0,5)$ से सबसे निकटस्थ बिंदु $( \pm 2 \sqrt{2}, 4)$ है। सही उत्तर है $A$।

हल

मान लीजिए $f(x)=\frac{1-x+x^{2}}{1+x+x^{2}}$।

$ \begin{aligned} \therefore f^{\prime}(x) & =\frac{(1+x+x^{2})(-1+2 x)-(1-x+x^{2})(1+2 x)}{(1+x+x^{2})^{2}} \\

$$ & =\frac{-1+2 x-x+2 x^{2}-x^{2}+2 x^{3}-1-2 x+x+2 x^{2}-x^{2}-2 x^{3}}{(1+x+x^{2})^{2}} \\ & =\frac{2 x^{2}-2}{(1+x+x^{2})^{2}}=\frac{2(x^{2}-1)}{(1+x+x^{2})^{2}} \end{aligned} $

$\therefore f^{\prime}(x)=0 \Rightarrow x^{2}=1 \Rightarrow x= \pm 1$

अब, $f^{\prime \prime}(x)=\frac{2[(1+x+x^{2})^{2}(2 x)-(x^{2}-1)(2)(1+x+x^{2})(1+2 x)]}{(1+x+x^{2})^{4}}$

$ =\frac{4(1+x+x^{2})[(1+x+x^{2}) x-(x^{2}-1)(1+2 x)]}{(1+x+x^{2})^{4}} $

$ \begin{aligned} & =\frac{4[x+x^{2}+x^{3}-x^{2}-2 x^{3}+1+2 x]}{(1+x+x^{2})^{3}} \\ & =\frac{4(1+3 x-x^{3})}{(1+x+x^{2})^{3}} \end{aligned} $

और, $f^{\prime \prime}(1)=\frac{4(1+3-1)}{(1+1+1)^{3}}=\frac{4(3)}{(3)^{3}}=\frac{4}{9}>0$

भी, $f^{\prime \prime}(-1)=\frac{4(1-3+1)}{(1-1+1)^{3}}=4(-1)=-4<0$

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, $f$ का न्यूनतम मान $x=1$ पर है और न्यूनतम मान द्वारा दिया गया है

$f(1)=\frac{1-1+1}{1+1+1}=\frac{1}{3}$.

सही उत्तर है $D$.

हल

मान लीजिए $f(x)=[x(x-1)+1]^{\frac{1}{3}}$.

$\therefore f^{\prime}(x)=\frac{2 x-1}{3[x(x-1)+1]^{\frac{2}{3}}}$

अब, $f^{\prime}(x)=0 \Rightarrow x=\frac{1}{2}$

फिर, हम अंतिम बिंदुओं $x=0$ और $x=1$ के अंतराल $[0,1]$ पर $f$ के मान का मूल्यांकन करते हैं।

$f(0)=[0(0-1)+1]^{\frac{1}{3}}=1$

$f(1)=[1(1-1)+1]^{\frac{1}{3}}=1$

$f(\frac{1}{2})=[\frac{1}{2}(\frac{-1}{2})+1]^{\frac{1}{3}}=(\frac{3}{4})^{\frac{1}{3}}$

इसलिए, हम निष्कर्ष निकाल सकते हैं कि अंतराल $[0,1]$ में $f$ का अधिकतम मान 1 है।

सही उत्तर है $C$.

हल

दिया गया फलन $f(x)=\frac{\log x}{x}$ है।

$ f^{\prime}(x)=\frac{x(\frac{1}{x})-\log x}{x^{2}}=\frac{1-\log x}{x^{2}} $

अब, $f^{\prime}(x)=0$

$\Rightarrow 1-\log x=0$ $\Rightarrow \log x=1$

$\Rightarrow \log x=\log e$

$\Rightarrow x=e$

अब, $f^{\prime \prime}(x)=\frac{x^{2}(-\frac{1}{x})-(1-\log x)(2 x)}{x^{4}}$

$ \begin{aligned} & =\frac{-x-2 x(1-\log x)}{x^{4}} \\ & =\frac{-3+2 \log x}{x^{3}} \end{aligned} $

अब, $f^{\prime \prime}(e)=\frac{-3+2 \log e}{e^{3}}=\frac{-3+2}{e^{3}}=\frac{-1}{e^{3}}<0$

इसलिए, द्वितीय अवकलज परीक्षण के अनुसार, $f$ का मान $x=e$ पर अधिकतम होता है।

हल

मान लीजिए $\triangle A B C$ एक समद्विबाहु त्रिभुज है जहाँ $B C$ निश्चित लंबाई का आधार $b$ है।

मान लीजिए $\triangle A B C$ की दो बराबर भुजाओं की लंबाई $a$ है।

AD $\square BC$ खींचिए।

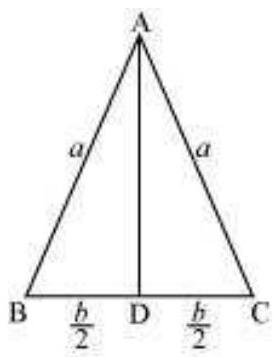
अब, $\triangle A D C$ में पिथागोरस प्रमेय के अनुसार, हमें प्राप्त होता है:

$AD=\sqrt{a^{2}-\frac{b^{2}}{4}}$

त्रिभुज का क्षेत्रफल

$ (A)=\frac{1}{2} b \sqrt{a^{2}-\frac{b^{2}}{4}} $

क्षेत्रफल के संबंध में समय $(t)$ के संबंध में परिवर्तन की दर निम्नलिखित है,

$\frac{d A}{d t}=\frac{1}{2} b \cdot \frac{2 a}{2 \sqrt{a^{2}-\frac{b^{2}}{4}}} \frac{d a}{d t}=\frac{a b}{\sqrt{4 a^{2}-b^{2}}} \frac{d a}{d t}$

दिया गया है कि त्रिभुज की दो बराबर भुजाएँ $3$ सेमी/सेकंड की दर से घट रही हैं।

$ \begin{aligned} & \\ & \square \frac{d a}{d t}=-3\ cm / s \\ & \therefore \frac{d A}{d t}=\frac{-3 a b}{\sqrt{4 a^{2}-b^{2}}} \end{aligned} $

फिर, जब $a=b$ हो, तो हमें प्राप्त होता है:

$\frac{d A}{d t}=\frac{-3 b^{2}}{\sqrt{4 b^{2}-b^{2}}}=\frac{-3 b^{2}}{\sqrt{3 b^{2}}}=-\sqrt{3} b$

इसलिए, यदि दो समान भुजाएँ आधार के बराबर हों, तो त्रिभुज का क्षेत्रफल $\sqrt{3} bm\ cm^{2} / s$ की दर से घट रहा है।

हल

$f(x)=\frac{4 \sin x-2 x-x \cos x}{2+\cos x}$

$\therefore f^{\prime}(x)=\frac{(2+\cos x)(4 \cos x-2-\cos x+x \sin x)-(4 \sin x-2 x-x \cos x)(-\sin x)}{(2+\cos x)^{2}}$

$=\frac{(2+\cos x)(3 \cos x-2+x \sin x)+\sin x(4 \sin x-2 x-x \cos x)}{(2+\cos x)^{2}}$

$=\frac{6 \cos x-4+2 x \sin x+3 \cos ^{2} x-2 \cos x+x \sin x \cos x+4 \sin ^{2} x-2 x \sin x-x \sin x \cos x}{(2+\cos x)^{2}}$

$=\frac{4 \cos x-4+3 \cos ^{2} x+4 \sin ^{2} x}{(2+\cos x)^{2}}$

$=\frac{4 \cos x-4+3 \cos ^{2} x+4-4 \cos ^{2} x}{(2+\cos x)^{2}}$

$=\frac{4 \cos x-\cos ^{2} x}{(2+\cos x)^{2}}=\frac{\cos x(4-\cos x)}{(2+\cos x)^{2}}$

अब, $f^{\prime}(x)=0$

$\Rightarrow \cos x=0$ या $\cos x=4$

लेकिन, $\cos x \neq 4$

$\square \cos x=0$

$\Rightarrow x=\frac{\pi}{2}, \frac{3 \pi}{2}$

अब, $x=\frac{\pi}{2}$ और $x=\frac{3 \pi}{2}$ अंतराल $(0,2 \pi)$ को तीन अलग-अलग अंतराल में विभाजित करते हैं, अर्थात,

$(0, \frac{\pi}{2}),(\frac{\pi}{2}, \frac{3 \pi}{2})$, और $(\frac{3 \pi}{2}, 2 \pi)$।

अंतराल $(0, \frac{\pi}{2})$ और $(\frac{3 \pi}{2}, 2 \pi)$ में $f^{\prime}(x)>0$ है।

इसलिए, $f(x)$ के लिए $0<x<\frac{x}{2}$ और $\frac{3 \pi}{2}<x<2 \pi$ में बढ़ रहा है।

अंतराल $(\frac{\pi}{2}, \frac{3 \pi}{2})$ में $f^{\prime}(x)<0$ है।

इसलिए, $f(x)$ के लिए $\frac{\pi}{2}<x<\frac{3 \pi}{2}$ में घट रहा है।

हल

$f(x)=x^{3}+\frac{1}{x^{3}}$

$\therefore f^{\prime}(x)=3 x^{2}-\frac{3}{x^{4}}=\frac{3 x^{6}-3}{x^{4}}$

फिर, $f^{\prime}(x)=0 \Rightarrow 3 x^{6}-3=0 \Rightarrow x^{6}=1 \Rightarrow x= \pm 1$

अब, बिंदु $x=1$ और $x=-1$ वास्तविक रेखा को तीन अलग-अलग अंतराल में विभाजित करते हैं

अर्थात, $(-\infty,-1),(-1,1)$, और $(1, \infty)$।

अंतराल $(-\infty,-1)$ और $(1, \infty)$ में, अर्थात जब $x<-1$ और $x>1, f^{\prime}(x)>0$ होता है।

इसलिए, जब $x<-1$ और $x>1, f$ बढ़ रहा है।

अंतराल $(-1,1)$ में, अर्थात जब $-1<x<1, f^{\prime}(x)<0$ होता है।

इसलिए, जब $-1<x<1, f$ घट रहा है।

हल

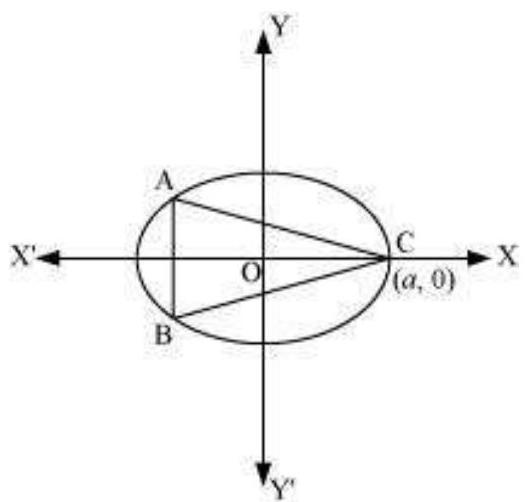
दिया गया वृत्त $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ है।

मान लीजिए मुख्य अक्ष $x$-अक्ष के अनुदिश है।

मान लीजिए $A B C$ वृत्त में अंकित एक त्रिभुज है जहाँ शीर्ष $C$ बिंदु $(a, 0)$ पर है।

चूंकि वृत्त $x$-अक्ष और $y$-अक्ष के संबंध में सममित है, हम मान सकते हैं कि $A$ के निर्देशांक $(-x_1, y_1)$ हैं और $B$ के निर्देशांक $(-x_1,-y_1)$ हैं।

अब, हमें $y_1= \pm \frac{b}{a} \sqrt{a^{2}-x_1^{2}}$ है।

$\square$ $A$ के निर्देशांक $(-x_1, \frac{b}{a} \sqrt{a^{2}-x_1^{2}})$ हैं और $B$ के निर्देशांक $(x_1,-\frac{b}{a} \sqrt{a^{2}-x_1^{2}})$ हैं।

जब बिंदु $(x_1, y_1)$ वृत्त पर स्थित होता है, तो त्रिभुज $ABC$ का क्षेत्रफल निम्नलिखित द्वारा दिया जाता है,

$ \begin{aligned} & A=\frac{1}{2}|a(\frac{2 b}{a} \sqrt{a^{2}-x_1^{2}})+(-x_1)(-\frac{b}{a} \sqrt{a^{2}-x_1^{2}})+(-x_1)(-\frac{b}{a} \sqrt{a^{2}-x_1^{2}})| \\

$$ \begin{aligned} & \Rightarrow A=b \sqrt{a^{2}-x_1^{2}}+x_1 \frac{b}{a} \sqrt{a^{2}-x_1^{2}} \\ & \therefore \frac{d A}{d x_1}=\frac{-2 x_1 b}{2 \sqrt{a^{2}-x_1^{2}}}+\frac{b}{a} \sqrt{a^{2}-x_1^{2}}-\frac{2 b x_1^{2}}{a 2 \sqrt{a^{2}-x_1^{2}}} \\ & =\frac{b}{a \sqrt{a^{2}-x_1^{2}}}[-x_1 a+(a^{2}-x_1^{2})-x_1^{2}] \\ & =\frac{b(-2 x_1^{2}-x_1 a+a^{2})}{a \sqrt{a^{2}-x_1^{2}}} \end{aligned} $$

अब, $\frac{d A}{d x_1}=0$

$\Rightarrow-2 x_1^{2}-x_1 a+a^{2}=0$

$\Rightarrow x_1=\frac{a \pm \sqrt{a^{2}-4(-2)(a^{2})}}{2(-2)}$

$=\frac{a \pm \sqrt{9 a^{2}}}{-4}$

$=\frac{a \pm 3 a}{-4}$

$\Rightarrow x_1=-a, \frac{a}{2}$

लेकिन, $x_1$ के मान $a$ के बराबर नहीं हो सकता। $\therefore x_1=\frac{a}{2} \Rightarrow y_1=\frac{b}{a} \sqrt{a^{2}-\frac{a^{2}}{4}}=\frac{b a}{2 a} \sqrt{3}=\frac{\sqrt{3} b}{2}$

अब, $\frac{d^{2} A}{d x_1^{2}}=\frac{b}{a}{\frac{\sqrt{a^{2}-x_1^{2}}(-4 x_1-a)-(-2 x_1^{2}-x_1 a+a^{2}) \frac{(-2 x_1)}{2 \sqrt{a^{2}-x_1^{2}}}}{a^{2}-x_1^{2}}}$

$ =\frac{b}{a}{\frac{(a^{2}-x_1^{2})(-4 x_1-a)+x_1(-2 x_1^{2}-x_1 a+a^{2})}{(a^{2}-x_1^{2})^{\frac{3}{2}}}} $

$ =\frac{b}{a}{\frac{2 x^{3}-3 a^{2} x-a^{3}}{(a^{2}-x_1^{2})^{\frac{3}{2}}}} $

इसके अतिरिक्त, जब $x_1=\frac{a}{2}$, तो

$ \begin{aligned} \frac{d^{2} A}{d x_1^{2}} & =\frac{b}{a}{\frac{2 \frac{a^{3}}{8}-3 \frac{a^{3}}{2}-a^{3}}{(\frac{3 a^{2}}{4})^{\frac{3}{2}}}}=\frac{b}{a}{\frac{\frac{a^{3}}{4}-\frac{3}{2} a^{3}-a^{3}}{(\frac{3 a^{2}}{4})^{\frac{3}{2}}}} \\ & =-\frac{b}{a}{\frac{\frac{9}{4} a^{3}}{(\frac{3 a^{2}}{4})^{\frac{3}{2}}}}<0 \end{aligned} $

इसलिए, जब $x_1=\frac{a}{2}$, तब क्षेत्रफल अधिकतम होता है।

$\square$ त्रिभुज का अधिकतम क्षेत्रफल निम्नलिखित है,

$ \begin{aligned} A & =b \sqrt{a^{2}-\frac{a^{2}}{4}}+(\frac{a}{2}) \frac{b}{a} \sqrt{a^{2}-\frac{a^{2}}{4}} \\ & =a b \frac{\sqrt{3}}{2}+(\frac{a}{2}) \frac{b}{a} \times \frac{a \sqrt{3}}{2} \\ & =\frac{a b \sqrt{3}}{2}+\frac{a b \sqrt{3}}{4}=\frac{3 \sqrt{3}}{4} a b \end{aligned} $

हल

मान लीजिए $l, b$, और $h$ क्रमशः टैंक की लंबाई, चौड़ाई और ऊंचाई को प्रस्तुत करते हैं।

तब, हमें ऊंचाई $(h)=2$ मीटर मिलती है।

टैंक का आयतन $=8$ मीटर³ है।

टैंक का आयतन $=l \times b \times h$

$\square 8=l \times b \times 2$

$\Rightarrow l b=4 \Rightarrow b=\frac{4}{l}$

अब, आधार का क्षेत्रफल $=I b=4$

चार दीवारों का क्षेत्रफल $(A)=2 h(I+b)$

$\therefore A=4(l+\frac{4}{l})$

$\Rightarrow \frac{d A}{d l}=4(1-\frac{4}{l^{2}})$

अब, $\frac{d A}{d l}=0$

$\Rightarrow 1-\frac{4}{l^{2}}=0$

$\Rightarrow l^{2}=4$

$\Rightarrow l= \pm 2$

हालांकि, लंबाई नकारात्मक नहीं हो सकती।

इसलिए, हमें $I=4$ मिलता है।

$\therefore b=\frac{4}{l}=\frac{4}{2}=2$

अब, $\frac{d^{2} A}{d l^{2}}=\frac{32}{l^{3}}$

जब $l=2, \frac{d^{2} A}{d l^{2}}=\frac{32}{8}=4>0$।

इसलिए, दूसरे अवकलज परीक्षण के अनुसार, क्षेत्रफल जब $I=2$ होता है तो न्यूनतम होता है।

हमें $I=b=h=2$ मिलता है।

$\square$ आधार के निर्माण की लागत $=70$ रुपये $\times (I b)=70(4)=280$ रुपये

दीवारों के निर्माण की लागत $=2 h(I+b) \times 45=90(2)(2+2)$

$=8(90)=720$ रुपये

अभीष्ट कुल लागत $=280+720=1000$ रुपये

इसलिए, टैंक की कुल लागत 1000 रुपये होगी।

हल

मान लीजिए $r$ वृत्त की त्रिज्या है और $a$ वर्ग की भुजा है।

तब, हमें दिया गया है:

$2 \pi r+4 a=k$ (जहाँ $k$ नियत संख्या है)

$\Rightarrow a=\frac{k-2 \pi r}{4}$

वृत्त और वर्ग के क्षेत्रफल के योग $(A)$ निम्नलिखित है,

$A=\pi r^{2}+a^{2}=\pi r^{2}+\frac{(k-2 \pi r)^{2}}{16}$

$\therefore \frac{d A}{d r}=2 \pi r+\frac{2(k-2 \pi r)(-2 \pi)}{16}=2 \pi r-\frac{\pi(k-2 \pi r)}{4}$

अब, $\frac{d A}{d r}=0$

$\Rightarrow 2 \pi r=\frac{\pi(k-2 \pi r)}{4}$

$8 r=k-2 \pi r$

$\Rightarrow(8+2 \pi) r=k$

$\Rightarrow r=\frac{k}{8+2 \pi}=\frac{k}{2(4+\pi)}$

अब, $\frac{d^{2} A}{d r^{2}}=2 \pi+\frac{\pi^{2}}{2}>0$

$\therefore$ जब $r=\frac{k}{2(4 \pi)}, \frac{d^{2} A}{d r^{2}}>0$।

जब $r=\frac{k}{2(4 \pi)}, a=\frac{k-2 \pi[\frac{k}{2(4 \pi)}]}{4}=\frac{k(4 \pi) \pi k}{4(\pi)}=\frac{4 k}{4(\pi)}=\frac{k}{\pi}=2 r$।

अतः सिद्ध कर दिया गया है कि वृत्त और वर्ग के क्षेत्रफल के योग कम से कम होता है जब वर्ग की भुजा वृत्त की त्रिज्या के दुगुनी होती है।

हल

मान लीजिए $x$ और $y$ आयताकार खिड़की की लंबाई और चौड़ाई है।

अर्धवृत्ताकार खोल की त्रिज्या $=\frac{x}{2}$

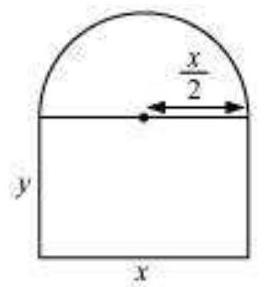
दिया गया है कि खिड़की का परिमाप $10 मीटर$ है।

$\therefore x+2 y+\frac{\pi x}{2}=10$

$\Rightarrow x(1+\frac{\pi}{2})+2 y=10$

$\Rightarrow 2 y=10-x(1+\frac{\pi}{2})$

$\Rightarrow y=5-x(\frac{1 \pi}{2}+\frac{-}{4})$

आवृत्ति क्षेत्रफल $(A)$ निम्नलिखित द्वारा दिया गया है,

$ \begin{aligned} A & =x y+\frac{\pi}{2}(\frac{x}{2})^{2} \\ & =x[5-x(\frac{1 \pi}{2}+\frac{\pi}{4})]+\frac{x^{2}}{8} \\ & =5 x-x^{2}(\frac{1 \pi}{2}+\frac{\pi}{4})+\frac{\pi}{8} x^{2} \\ \therefore & \frac{d A}{d x}=5-2 x(\frac{1 \pi}{2}+\frac{\pi}{4})+\frac{\pi}{4} x \\ & =5-x(1+\frac{\pi}{2})+\frac{\pi}{4} x \\ \therefore & \frac{d^{2} A}{d x^{2}}=-(1+\frac{\pi}{2})+\frac{\pi}{4}=-1-\frac{\pi}{4} \end{aligned} $

अब, $\frac{d A}{d x}=0$

$\Rightarrow 5-x(1+\frac{\pi}{2})+\frac{\pi}{4} x=0$

$\Rightarrow 5-x-\frac{\pi}{4} x=0$

$\Rightarrow x(1+\frac{\pi}{4})=5$

$\Rightarrow x=\frac{5}{(1+\frac{\pi}{4})}=\frac{20}{\pi+4}$

अतः जब $x=\frac{20}{\pi+4}$ तो $\frac{d^{2} A}{d x^{2}}<0$।

इसलिए, द्वितीय अवकलज परीक्षण के अनुसार, क्षेत्रफल अधिकतम होता है जब लंबाई $x=\frac{20}{\pi+4} m$ हो। अब,

$y=5-\frac{20}{\pi+4}(\frac{2+\pi}{4})=5-\frac{5(2+\pi)}{\pi+4}=\frac{10}{\pi+4} m$

इसलिए, अधिकतम प्रकाश प्रवेश करने वाले खिड़की के आवश्यक आयाम द्वारा दिए गए हैं

लंबाई $=\frac{20}{\pi+4} m$ और चौड़ाई $=\frac{10}{\pi+4} m$।

हल

मान लीजिए $\triangle A B C$ बिंदु $B$ पर समकोण है। मान लीजिए $A B=x$ और $B C=y$।

मान लीजिए $P$ त्रिभुज के कर्ण पर एक बिंदु है जैसे कि $P$ भुजा $A B$ और $B C$ से क्रमशः $a$ और $b$ की दूरी पर है।

मान लीजिए $\square C=\theta$।

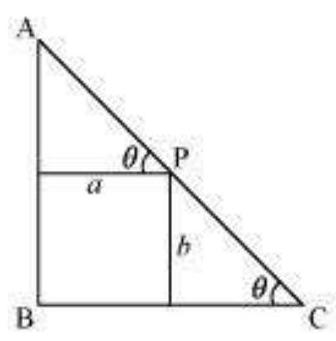
हमारे पास,

$AC=\sqrt{x^{2}+y^{2}}$

अब,

$PC=b cosec \theta$

और, $AP=a \sec \theta$

$\square AC=AP+PC$

$\square AC=b cosec \theta+a \sec \theta \ldots$ (1)

$\therefore \frac{d(AC)}{d \theta}=-b cosec \theta \cot \theta+a \sec \theta \tan \theta$

$\therefore \frac{d(AC)}{d \theta}=0$

$\Rightarrow a \sec \theta \tan \theta=b cosec \theta \cot \theta$

$\Rightarrow \frac{a}{\cos \theta} \cdot \frac{\sin \theta}{\cos \theta}=\frac{b}{\sin \theta} \frac{\cos \theta}{\sin \theta}$

$\Rightarrow a \sin ^{3} \theta=b \cos ^{3} \theta$

$\Rightarrow(a)^{\frac{1}{3}} \sin \theta=(b)^{\frac{1}{3}} \cos \theta$

$\Rightarrow \tan \theta=(\frac{b}{a})^{\frac{1}{3}}$

$\therefore \sin \theta=\frac{(b)^{\frac{1}{3}}}{\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}$ और $\cos \theta=\frac{(a)^{\frac{1}{3}}}{\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}$

स्पष्ट रूप से दिखाया जा सकता है कि $\frac{d^{2}(AC)}{d \theta^{2}}<0$ जब $\tan \theta=(\frac{b}{a})^{\frac{1}{3}}$।

इसलिए, द्वितीय अवकलज परीक्षण के अनुसार, तीन कोण की लंबाई अधिकतम होती है जब

$\tan \theta=(\frac{b}{a})^{\frac{1}{3}}$.

अब, जब $\tan \theta=(\frac{b}{a})^{\frac{1}{3}}$, हम निम्नलिखित प्राप्त करते हैं:

$ \begin{aligned} AC & =\frac{b \sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}{b^{\frac{1}{3}}}+\frac{a \sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}{a^{\frac{1}{3}}} \\ & =\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}(b^{\frac{2}{3}}+a^{\frac{2}{3}}) \\ & =(a^{\frac{2}{3}}+b^{\frac{2}{3}})^{\frac{3}{2}} \end{aligned} $

इसलिए, अधिकतम तीन कोण की लंबाई $(a^{\frac{2}{3}}+b^{\frac{2}{3}})^{\frac{3}{2}}$ है।

हल

दिया गया फलन $f(x)=(x-2)^{4}(x+1)^{3}$ है।

$ \begin{aligned} \therefore f^{\prime}(x) & =4(x-2)^{3}(x+1)^{3}+3(x+1)^{2}(x-2)^{4} \\ & =(x-2)^{3}(x+1)^{2}[4(x+1)+3(x-2)] \\ & =(x-2)^{3}(x+1)^{2}(7 x-2) \end{aligned} $

अब, $f^{\prime}(x)=0 \Rightarrow x=-1$ और $x=\frac{2}{7}$ या $x=2$

अब, $x$ के मान जो $\frac{2}{7}$ के निकट हों और $\frac{2}{7}$ के बाईं ओर हों, $f^{\prime}(x)>0$ होता है। इसके अतिरिक्त, $x$ के मान जो $\frac{2}{7}$ के निकट हों और $\frac{2}{7}$ के दाईं ओर हों, $f^{\prime}(x)<0$ होता है।

इसलिए, $x=\frac{2}{7}$ स्थानीय उच्चिष्ठ बिंदु है।

अब, $x$ के मान जो 2 के निकट हों और 2 के बाईं ओर हों, $f^{\prime}(x)<0$ होता है। इसके अतिरिक्त, $x$ के मान जो 2 के निकट हों और 2 के दाईं ओर हों, $f^{\prime}(x)>0$ होता है।

इसलिए, $x=2$ स्थानीय निम्निष्ठ बिंदु है।

अब, $x$ के मान जो $-1$ के माध्यम से चलते हैं, $f^{\prime}(x)$ अपना चिह्न बदलता नहीं है।

इसलिए, $x=-1$ वक्रता परिवर्तन बिंदु है।

हल

$ \begin{aligned} f(x) & =\cos ^{2} x+\sin x \\ f^{\prime}(x) & =2 \cos x(-\sin x)+\cos x \\ & =-2 \sin x \cos x+\cos x

\end{aligned} $

अब, $f^{\prime}(x)=0$

$\Rightarrow 2 \sin x \cos x=\cos x \Rightarrow \cos x(2 \sin x-1)=0$

$\Rightarrow \sin x=\frac{1}{2}$ या $\cos x=0$

$\Rightarrow x=\frac{\pi}{6}$, या $\frac{\pi}{2}$ क्योंकि $x \in[0, \pi]$

अब, अंतराल $[0, \pi]$ के क्रिटिकल बिंदुओं $x=\frac{\pi}{2}$ और $x=\frac{\pi}{6}$ तथा अंतिम बिंदुओं (अर्थात $x=0$ और $x=\pi$) पर $f$ के मान का मूल्यांकन करते हैं, हम पाते हैं: $f(\frac{\pi}{6})=\cos ^{2} \frac{\pi}{6}+\sin \frac{\pi}{6}=(\frac{\sqrt{3}}{2})^{2}+\frac{1}{2}=\frac{5}{4}$

$f(0)=\cos ^{2} 0+\sin 0=1+0=1$

$f(\pi)=\cos ^{2} \pi+\sin \pi=(-1)^{2}+0=1$

$f(\frac{\pi}{2})=\cos ^{2} \frac{\pi}{2}+\sin \frac{\pi}{2}=0+1=1$

इसलिए, $f$ का अंतिम अधिकतम मान $\frac{5}{4}$ है जो $x=\frac{\pi}{6}$ पर होता है और $f$ का अंतिम न्यूनतम मान 1 है जो $x=0, \frac{\pi}{2}$ और $\pi$ पर होता है।

हल

एक निश्चित त्रिज्या $(r)$ वाला एक गोला दिया गया है।

मान लीजिए $R$ और $h$ क्रमशः बेलन की त्रिज्या और ऊंचाई है।

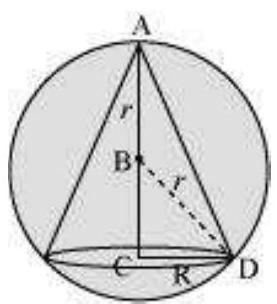
बेलन का आयतन $(V)$ निम्नलिखित द्वारा दिया गया है,

$V=\frac{1}{3} \pi R^{2} h$

अब, समकोण त्रिभुज $BCD$ से हम पाते हैं:

$BC=\sqrt{r^{2}-R^{2}}$

$\square h=r+\sqrt{r^{2}-R^{2}}$

$ \begin{aligned} & \therefore V=\frac{1}{3} \pi R^{2}(r+\sqrt{r^{2}-R^{2}})=\frac{1}{3} \pi R^{2} r+\frac{1}{3} \pi R^{2} \sqrt{r^{2}-R^{2}} \\ & \begin{aligned} \therefore \frac{d V}{d R} & =\frac{2}{3} \pi R r+\frac{2 \pi}{3} \pi R \sqrt{r^{2}-R^{2}}+\frac{R^{2}}{3} \cdot \frac{(-2 R)}{2 \sqrt{r^{2}-R^{2}}} \\ & =\frac{2}{3} \pi R r+\frac{2 \pi}{3} \pi R \sqrt{r^{2}-R^{2}}-\frac{R^{3}}{3 \sqrt{r^{2}-R^{2}}} \\

$$ \begin{aligned} & =\frac{2}{3} \pi R r+\frac{2 \pi R(r^{2}-R^{2})-\pi R^{3}}{3 \sqrt{r^{2}-R^{2}}} \\ & =\frac{2}{3} \pi R r+\frac{2 \pi R r^{2}-3 \pi R^{3}}{3 \sqrt{r^{2}-R^{2}}} \end{aligned} $$ $$ \end{aligned} $$

अब, $\frac{d V}{d R^{2}}=0$

$\Rightarrow \frac{2 \pi r R}{3}=\frac{3 \pi R^{3}-2 \pi R r^{2}}{3 \sqrt{r^{2}-R^{2}}}$

$\Rightarrow 2 r \sqrt{r^{2}-R^{2}}=3 R^{2}-2 r^{2}$

$\Rightarrow 4 r^{2}(r^{2}-R^{2})=(3 R^{2}-2 r^{2})^{2}$

$\Rightarrow 4 r^{4}-4 r^{2} R^{2}=9 R^{4}+4 r^{4}-12 R^{2} r^{2}$

$\Rightarrow 9 R^{4}-8 r^{2} R^{2}=0$

$\Rightarrow 9 R^{2}=8 r^{2}$

$\Rightarrow R^{2}=\frac{8 r^{2}}{9}$

अब, $\frac{d^{2} V}{d R^{2}}=\frac{2 \pi r}{3}+\frac{3 \sqrt{r^{2}-R^{2}}(2 \pi r^{2}-9 \pi R^{2})-(2 \pi R r^{2}-3 \pi R^{3})(-6 R) \frac{1}{2 \sqrt{r^{2}-R^{2}}}}{9(r^{2}-R^{2})}$

$ =\frac{2 \pi r}{3}+\frac{3 \sqrt{r^{2}-R^{2}}(2 \pi r^{2}-9 \pi R^{2})+(2 \pi R r^{2}-3 \pi R^{3})(3 R) \frac{1}{2 \sqrt{r^{2}-R^{2}}}}{9(r^{2}-R^{2})} $

अब, जब $R^{2}=\frac{8 r^{2}}{9}$, तो दिखाया जा सकता है कि $\frac{d^{2} V}{d R^{2}}<0$।

$\square$ जब आयतन अधिकतम होता है, तो

$ R^{2}=\frac{8 r^{2}}{9} $

जब $R^{2}=\frac{8 r^{2}}{9}$, तो शंकु की ऊँचाई $=r+\sqrt{r^{2}-\frac{8 r^{2}}{9}}=r+\sqrt{\frac{r^{2}}{9}}=r+\frac{r}{3}=\frac{4 r}{3}$।

इसलिए, देखा जा सकता है कि त्रिज्या $r$ वाले गोले में अंकित अधिकतम आयतन वाले समकोण वृत्तीय शंकु की ऊँचाई $\frac{4 r}{3}$ होती है।

Solution

हम कोई दो बिंदु $\mathrm{c}_1$ और $\mathrm{c}_2$ लेते हैं ताकि

${\mathrm{c} _1, \mathrm{c} _2} \in(\mathrm{a}, \mathrm{b})$ और

$\mathrm{c} _2=\mathrm{c} _1+\mathrm{h}$,

जहाँ $\mathrm{h} \rightarrow \mathrm{O}$

अब, $f^{\prime}\left(c _1\right)=\lim _{h \rightarrow 0} \frac{f\left(c _1+h\right)-f\left(c _1\right)}{h}=\frac{f\left(c _2\right)-f\left(c _1\right)}{c _2-c _1}$

अब, यह दिया गया है कि $\mathrm{f}^{\prime}(\mathrm{x})>0 \quad \forall \mathrm{x} \in(\mathrm{a}, \mathrm{b})$. इसलिए, $\mathrm{f}^{\prime}\left(\mathrm{c}_1\right)>0$

$\Rightarrow \frac{\mathrm{f}\left(\mathrm{c}_2\right)-\mathrm{f}\left(\mathrm{c}_1\right)}{\mathrm{c}_2-\mathrm{c}_1}>\mathrm{O}$

ऊपर के अंश से, हम निष्कर्ष निकाल सकते हैं कि:

1. $\mathrm{c}_2>\mathrm{c}_1$ के लिए, $\mathrm{f}\left(\mathrm{c}_2\right)>\mathrm{f}\left(\mathrm{c}_1\right)$

2. $c_1>c_2$ के लिए, $f\left(c_1\right)>f\left(c_2\right)$

इसलिए, $\mathrm{f}(\mathrm{x})$ अंतराल $(\mathrm{a}, \mathrm{b})$ में एक बढ़ती फलन है।

हल

एक निश्चित त्रिज्या $(R)$ वाले गोले को दिया गया है।

मान लीजिए $r$ और $h$ क्रमशः बेलन की त्रिज्या और ऊंचाई है।

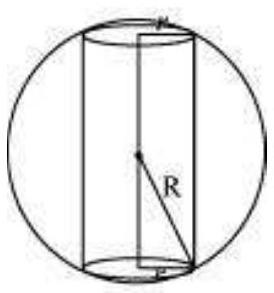
दिए गए चित्र से, हमें $h=2 \sqrt{R^{2}-r^{2}}$ मिलता है।

बेलन के आयतन $(V)$ को निम्नलिखित द्वारा दिया गया है,

$ \begin{aligned} & V=\pi r^{2} h=2 \pi r^{2} \sqrt{R^{2}-r^{2}} \\ & \begin{aligned} \therefore \frac{d V}{d r} & =4 \pi r \sqrt{R^{2}-r^{2}}+\frac{2 \pi r^{2}(-2 r)}{2 \sqrt{R^{2}-r^{2}}} \\ & =4 \pi r \sqrt{R^{2}-r^{2}}-\frac{2 \pi r^{3}}{\sqrt{R^{2}-r^{2}}} \\ & =\frac{4 \pi r(R^{2}-r^{2})-2 \pi r^{3}}{\sqrt{R^{2}-r^{2}}} \\ & =\frac{4 \pi r R^{2}-6 \pi r^{3}}{\sqrt{R^{2}-r^{2}}} \end{aligned} \end{aligned} $

अब, $\frac{d V}{d r}=0 \Rightarrow 4 \pi r R^{2}-6 \pi r^{3}=0$

$\Rightarrow r^{2}=\frac{2 R^{2}}{3}$

अब, $\frac{d^{2} V}{d r^{2}}=\frac{\sqrt{R^{2}-r^{2}}(4 \pi R^{2}-18 \pi r^{2})-(4 \pi r R^{2}-6 \pi r^{3}) \frac{(-2 r)}{2 \sqrt{R^{2}-r^{2}}}}{(R^{2}-r^{2})}$

$ \begin{aligned} & =\frac{(R^{2}-r^{2})(4 \pi R^{2}-18 \pi r^{2})+r(4 \pi r R^{2}-6 \pi r^{3})}{(R^{2}-r^{2})^{\frac{3}{2}}} \\ & =\frac{4 \pi R^{4}-22 \pi r^{2} R^{2}+12 \pi r^{4}+4 \pi r^{2} R^{2}}{(R^{2}-r^{2})^{\frac{3}{2}}} \end{aligned} $

अब, यह देखा जा सकता है कि $r^{2}=\frac{2 R^{2}}{3}$ पर, $\frac{d^{2} V}{d r^{2}}<0$ होता है।

$\square$ जब $r^{2}=\frac{2 R^{2}}{3}$, तब बेलन का आयतन अधिकतम होता है।

जब $r^{2}=\frac{2 R^{2}}{3}$, तब बेलन की ऊँचाई $2 \sqrt{R^{2}-\frac{2 R^{2}}{3}}=2 \sqrt{\frac{R^{2}}{3}}=\frac{2 R}{\sqrt{3}}$ होती है।

अतः, जब बेलन की ऊँचाई $\frac{2 R}{\sqrt{3}}$ होती है, तब बेलन का आयतन अधिकतम होता है।

हल

दिए गए एक निश्चित ऊँचाई $(h)$ और अर्ध-शीर्षकोण $(\alpha)$ वाले समकोण वृताकार शंकु को निम्नलिखित चित्र में बर्क लिया जा सकता है:

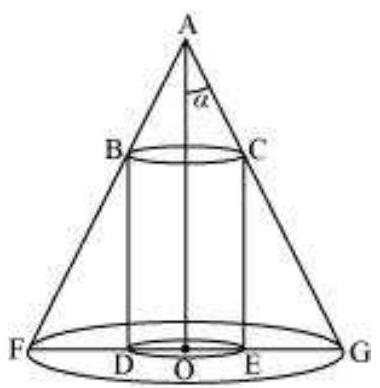
यहाँ, एक बेलन जिसकी त्रिज्या $R$ और ऊँचाई $H$ है, शंकु में आकृति बनाता है।

तब, $\square GAO=a, OG=r, OA=h, OE=R$, और $CE=H$ होता है।

हम जानते हैं,

$r=h \tan a$

अब, क्योंकि $\triangle AOG$ और $\triangle CEG$ समानुपाती हैं, हम लिख सकते हैं:

$\frac{AO}{OG}=\frac{CE}{EG}$

$\Rightarrow \frac{h}{r}=\frac{H}{r-R} \quad[EG=OG-OE]$

$\Rightarrow H=\frac{h}{r}(r-R)=\frac{h}{h \tan \alpha}(h \tan \alpha-R)=\frac{1}{\tan \alpha}(h \tan \alpha-R)$

अब, बेलन का आयतन $(V)$ निम्नलिखित द्वारा दिया जाता है,

$V=\pi R^{2} H=\frac{\pi R^{2}}{\tan \alpha}(h \tan \alpha-R)=\pi R^{2} h-\frac{\pi R^{3}}{\tan \alpha}$

$\therefore \frac{d V}{d R}=2 \pi R h-\frac{3 \pi R^{2}}{\tan \alpha}$

अब, $\frac{d V}{d R}=0$

$\Rightarrow 2 \pi R h=\frac{3 \pi R^{2}}{\tan \alpha}$

$\Rightarrow 2 h \tan \alpha=3 R$

$\Rightarrow R=\frac{2 h}{3} \tan \alpha$

अब, $\frac{d^{2} V}{d R^{2}}=2 \pi h-\frac{6 \pi R}{\tan \alpha}$

और, $R=\frac{2 h}{3} \tan \alpha$ के लिए, हम निम्नलिखित प्राप्त करते हैं:

$\frac{d^{2} V}{d R^{2}}=2 \pi h-\frac{6 \pi}{\tan \alpha}(\frac{2 h}{3} \tan \alpha)=2 \pi h-4 \pi h=-2 \pi h<0$

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, बेलन का आयतन जब $R=\frac{2 h}{3} \tan \alpha$ होता है, तब सबसे अधिक होता है।

जब $R=\frac{2 h}{3} \tan \alpha, H=\frac{1}{\tan \alpha}(h \tan \alpha-\frac{2 h}{3} \tan \alpha)=\frac{1}{\tan \alpha}(\frac{h \tan \alpha}{3})=\frac{h}{3}$।

अतः, जब बेलन का आयतन सबसे अधिक होता है, तब बेलन की ऊँचाई शंकु की ऊँचाई के एक-तिहाई होती है।

अब, बेलन के अधिकतम आयतन को निम्नलिखित तरीके से प्राप्त किया जा सकता है:

$\pi(\frac{2 h}{3} \tan \alpha)^{2}(\frac{h}{3})=\pi(\frac{4 h^{2}}{9} \tan ^{2} \alpha)(\frac{h}{3})=\frac{4}{27} \pi h^{3} \tan ^{2} \alpha$

अतः, दिए गए परिणाम की पुष्टि कर दी गई है।

हल

मान लीजिए $r$ बेलन की त्रिज्या है।

तब, बेलन का आयतन $(V)$ निम्नलिखित द्वारा दिया जाता है,

$V=\pi(\text{ त्रिज्या })^{2} \times$ ऊँचाई

$ \begin{matrix} =\pi(10)^{2} h & (\text{ त्रिज्या }=10 m) \\ =100 \pi h \end{matrix} $

समय $t$ के सापेक्ष अवकलन करने पर, हम निम्नलिखित प्राप्त करते हैं:

$\frac{d V}{d t}=100 \pi \frac{d h}{d t}$

टैंक 314 घन मीटर प्रति घंटा की दर से गेहूँ से भर रहा है।

$ \square \frac{d V}{d t}=314 m^{3} / h $

इसलिए, हम निम्नलिखित प्राप्त करते हैं:

$ \begin{aligned} & 314=100 \pi \frac{d h}{d t} \\ & \Rightarrow \frac{d h}{d t}=\frac{314}{100(3.14)}=\frac{314}{314}=1 \end{aligned} $

इसलिए, गेहूँ की गहराई की वृद्धि दर $1 m / h$ है।

सही उत्तर $A$ है।