अधिकांश विज्ञानों में एक पीढ़ी द्वारा दूसरी पीढ़ी द्वारा निर्मित कार्य को ध्वस कर देती है और जो एक पीढ़ी द्वारा स्थापित किया गया होता है उसे दूसरी पीढ़ी द्वारा अस्त बर्बाद कर देती है। गणित में अकेले प्रत्येक पीढ़ी पुरानी संरचना के लिए एक नया कहानी बनाती है। - हरमन हैंकेल

10.1 परिचय

हमारे दैनिक जीवन में हम बहुत से प्रश्नों के सामने आते हैं जैसे कि - आपकी ऊंचाई क्या है? एक फुटबॉल खिलाड़ी कैसे गेंद को मारे ताकि अपनी टीम के दूसरे खिलाड़ी को पास कर सके? ध्यान दें कि पहले प्रश्न के संभावित उत्तर के लिए 1.6 मीटर एक संभावित उत्तर हो सकता है, जो केवल एक मान (मापदंड) के साथ एक वास्तविक संख्या होती है। ऐसे मानों को सदिश कहते हैं। हालांकि, दूसरे प्रश्न के उत्तर के लिए एक मान (बल कहलाता है) जो मापदंड (मांसपेशियों की शक्ति) और दिशा (दूसरे खिलाड़ी के स्थिति) के साथ संबंधित होता है। ऐसे मानों को सदिश कहते हैं। गणिज्ञान, भौतिकी और इंजीनियरिंग में हम दोनों प्रकार के मानों के साथ अक्सर सामना करते हैं, जैसे कि सदिश मान जैसे विस्थापन, वेग, त्वरण, बल, भार, गति, विद्युत क्षेत्र तीव्रता आदि और अदिश मान जैसे लंबाई, द्रव्यमान, समय, दूरी, चाल, क्षेत्रफल, आयतन, तापमान, कार्य, पैसा, वोल्टेज, घनत्व, प्रतिरोध आदि।

W.R. हैमिल्टन $(1805-1865)$

इस अध्याय में, हम सदिशों के बारे में कुछ मूल अवधारणाओं, सदिशों पर विभिन्न संचालन और उनके बीजगणितीय और ज्यामितीय गुणों के बारे में अध्ययन करेंगे। इन दो प्रकार के गुणों को एक साथ ध्यान में लेने पर सदिश के अवधारणा के पूर्ण रूप को दर्शाया जाता है और उपरोक्त क्षेत्रों में उनके महत्वपूर्ण अनुप्रयोग को दर्शाता है।

10.2 कुछ मूल अवधारणाएं

मान लीजिए ’ $l$ ’ कोई भी सीधी रेखा तल या तीन आयामी अंतरिका में हो। इस रेखा को तीन दिशाओं में बताने के लिए तीन तीरों के साथ दिखाया जा सकता है। एक रेखा जिसमें इन दिशाओं में से एक निर्धारित की गई हो उसे निर्देशित रेखा कहते हैं (चित्र 10.1 (i), (ii))।

चित्र 10.1

अब ध्यान दें कि यदि हम रेखा $l$ को रेखाखंड AB के रूप में सीमित कर दें, तो रेखा $l$ पर एक मापदंड निर्धारित कर देंगे जिसमें दोनों दिशाओं में से एक दिशा हो, ताकि हमें एक अभिमुख रेखाखंड (चित्र 10.1(iii)) प्राप्त होता है। इस प्रकार, एक अभिमुख रेखाखंड में मापदंड और दिशा दोनों होते हैं।

परिभाषा 1 एक राशि जो मापदंड और दिशा दोनों होती है, एक सदिश कहलाती है।

ध्यान दें कि एक अभिमुख रेखाखंड एक सदिश होता है (चित्र 10.1(iii)), जिसे $\overrightarrow{{}AB}$ या साधारणतः $\vec{a}$ के रूप में लिखा जाता है, और इसे ‘सदिश $\overrightarrow{{}AB}$’ या ‘सदिश $\vec{a}$’ कहा जाता है।

सदिश $\overrightarrow{{}AB}$ से जहां सदिश शुरू होती है उस बिंदु $A$ को इसका प्रारंभिक बिंदु कहते हैं, और जहां सदिश समाप्त होती है उस बिंदु $B$ को इसका अंतिम बिंदु कहते हैं। एक सदिश के प्रारंभिक और अंतिम बिंदुओं के बीच दूरी को इस सदिश के मापदंड (या लंबाई) कहते हैं, जिसे $|\overrightarrow{{}AB}|$, या $|\vec{a}|$, या $a$ से नोट किया जाता है। तीर दिशा को दर्शाता है।

नोट क्योंकि लंबाई कभी नकारात्मक नहीं होती, इसलिए $|\vec{a}|<0$ के नोटेशन का कोई अर्थ नहीं होता।

स्थिति सदिश

कक्षा XI से, आप तीन आयामी दाएं हाथ के आयताकार निर्देशांक प्रणाली के बारे में याद कर सकते हैं (चित्र 10.2(i))। मान लीजिए अंतरिका में एक बिंदु $P$ है, जिसके संबंध में उत्पति $O(0,0,0)$ के संबंध में निर्देशांक $(x, y, z)$ हैं। तब, वह सदिश $\overrightarrow{{}OP}$ जिसके प्रारंभिक बिंदु $O$ और अंतिम बिंदु $P$ होते हैं, बिंदु $P$ के संबंध में उत्पति $O$ के संबंध में स्थिति सदिश कहलाती है। दूरी सूत्र (कक्षा XI से) का उपयोग करते हुए, सदिश $\overrightarrow{{}OP}$ (या $\vec{r}$) के मापदंड को निम्नलिखित द्वारा दिया जाता है:

$ \qquad \qquad |\overrightarrow{{}OP}|=\sqrt{x^{2}+y^{2}+z^{2}} $

अभ्यास में, बिंदुओं $A, B, C$ आदि के संबंध में उत्पति $O$ के संबंध में स्थिति सदिश को क्रमशः $\vec{a}, \vec{b}, \vec{c}$ आदि द्वारा नोट किया जाता है (चित्र 10.2 (ii)).

चित्र 10.2

दिशा कोज्याएँ

किसी बिंदु $P(x, y, z)$ के स्थिति सदिश $\overrightarrow{{}OP}$ (या $\vec{r}$) को चित्र 10.3 में देखा जा सकता है। इस सदिश $\vec{r}$ के $x$, $y$ और $z$-अक्ष के धनात्मक दिशा के साथ बनाए गए कोण $\alpha$, $\beta, \gamma$ को इसके दिशा कोण कहा जाता है। इन कोणों के कोज्याएँ, अर्थात $\cos \alpha, \cos \beta$ और $\cos \gamma$ को इस सदिश $\vec{r}$ के दिशा कोज्याएँ कहा जाता है, और आमतौर पर $l, m$ और $n$ से प्रदर्शित किया जाता है।

चित्र 10 बी.3

चित्र 10.3 से एक नोट कर सकते हैं कि त्रिभुज OAP समकोण है, और इसमें हम $\cos \alpha=\dfrac{x}{r}$ (जहाँ $r$ के लिए $|\vec{r}|$ है) प्राप्त कर सकते हैं। इसी तरह, समकोण त्रिभुज OBP और OCP से हम $\cos \beta=\dfrac{y}{r}$ और $\cos \gamma=\dfrac{z}{r}$ लिख सकते हैं। इस प्रकार, बिंदु P के निर्देशांक भी $(l r, m r, n r)$ के रूप में व्यक्त किए जा सकते हैं। संख्याएँ $l r, m r$ और $n r$, जो दिशा कोज्याओं के अनुपात में होती हैं, सदिश $\vec{r}$ के दिशा अनुपात कहलाती हैं, और इन्हें $a, b$ और $c$ से प्रदर्शित किया जाता है।

नोट एक नोट कर सकते हैं कि $l^{2}+m^{2}+n^{2}=1$ लेकिन $a^{2}+b^{2}+c^{2} \neq 1$, सामान्य रूप से।

10.3 सदिशों के प्रकार

शून्य सदिश एक सदिश जिसके प्रारंभिक और समापन बिंदु एक ही हों, शून्य सदिश (या शून्य सदिश) कहलाता है, और $\overrightarrow{{}0}$ से प्रदर्शित किया जाता है। शून्य सदिश के लिए एक निश्चित दिशा निर्धारित नहीं की जा सकती क्योंकि इसके मापांक शून्य है। या अलग रूप से, इसे किसी भी दिशा के रूप में ले सकते हैं। सदिश $\overrightarrow{{}AA}, \overrightarrow{{}BB}$ शून्य सदिश को प्रदर्शित करते हैं।

एकक सदिश एक सदिश जिसके मापांक एक (अर्थात 1 इकाई) होता है, एकक सदिश कहलाता है। एक दिए गए सदिश $\vec{a}$ की दिशा में एकक सदिश को $\hat{a}$ से प्रदर्शित किया जाता है।

सह-प्रारंभिक सदिश दो या अधिक सदिश जिनके प्रारंभिक बिंदु एक ही होते हैं, सह-प्रारंभिक सदिश कहलाते हैं।

संरेख सदिश दो या अधिक सदिश संरेख कहलाते हैं यदि वे एक ही रेखा के समानांतर हों, चाहे उनके मापांक और दिशा किसी भी हो।

समान सदिश दो सदिश $\vec{a}$ और $\vec{b}$ तब समान कहलाते हैं, जब वे समान परिमाण और दिशा रखते हों, चाहे उनके प्रारंभिक बिंदुओं के स्थान के अतिरिक्त कुछ भी न हो, और इन्हें $\vec{a}=\vec{b}$ के रूप में लिखा जाता है।

एक सदिश का ऋणात्मक एक सदिश के परिमाण के समान परिमाण वाला एक सदिश जिसकी दिशा दिए गए सदिश (मान लीजिए $\overrightarrow{{}AB}$) के विपरीत हो, दिए गए सदिश का ऋणात्मक कहलाता है। उदाहरण के लिए, सदिश $\overrightarrow{{}BA}$ दिए गए सदिश $\overrightarrow{{}AB}$ का ऋणात्मक होता है, और इसे $\overrightarrow{{}BA}=-\overrightarrow{{}AB}$ के रूप में लिखा जाता है।

टिप्पणी ऊपर वर्णित सदिश ऐसे होते हैं जिनके आवश्यकता अनुसार उनके परिमाण और दिशा को बदले बिना उनके समान्तर विस्थापन के लिए उपलब्ध हो सकते हैं। ऐसे सदिश को मुक्त सदिश कहते हैं। इस पाठ्यक्रम में हम मुक्त सदिश के बारे में ही बात करेंगे।

उदाहरण 1 एक विस्थापन को आलेखीय रूप में प्रस्तुत करें जो $40 ~\text{किमी}, 30^{\circ}$ दक्षिण के पश्चिम में हो।

हल सदिश $\overrightarrow{{}OP}$ आवश्यक विस्थापन को दर्शाता है (चित्र 10.4)।

चित्र 10.4

उदाहरण 2 निम्नलिखित मापदंडों को सदिश और अदिश के रूप में वर्गीकृत करें।

(i) $5 \mathrm{s}$

(ii) $1000 \mathrm{~cm}^{3}$

(iii) $10 \mathrm{~N}$

(iv) $30 \mathrm{~km} / \mathrm{h}$

(v) $10 \mathrm{~g} / \mathrm{cm}^{3}$

(vi) $20 m / s$ उत्तर की ओर

हल

(i) समय - अदिश

(ii) आयतन - अदिश

(iii) बल - सदिश

(iv) चाल - अदिश

(v) घनत्व - अदिश

(vi) वेग - सदिश

उदाहरण 3 चित्र 10.5 में निम्नलिखित में से कौन से सदिश:

(i) समरेख

(ii) समान

(iii) समारंभिक

हल

(i) समरेख सदिश: $\vec{a}, \vec{c}$ और $\vec{d}$

(ii) समान सदिश: $\vec{a}$ और $\vec{c}$

(iii) समारंभिक सदिश: $\vec{b}, \vec{c}$ और $\vec{d}$

अभ्यास 10.1

1. 40 किमी, उत्तर के 30° पूर्व के विस्थापन को ग्राफ़िकल रूप से प्रस्तुत करें।

उत्तर दिखाएं

हल

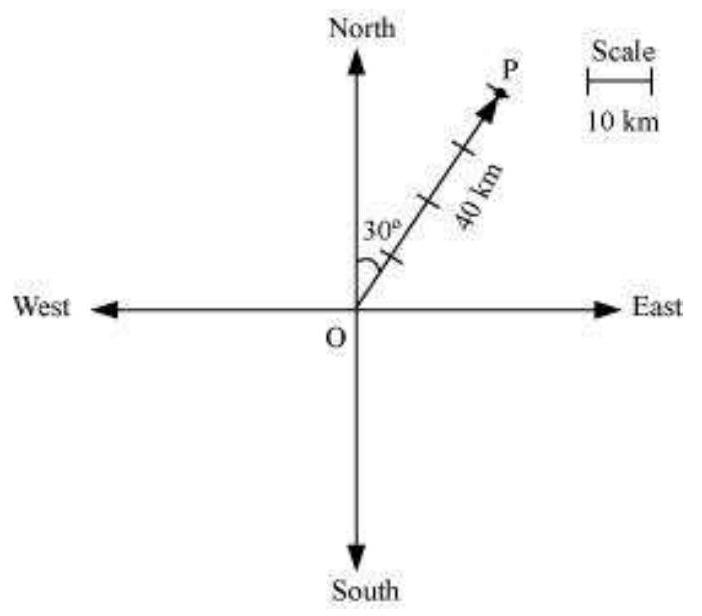
यहाँ, सदिश $\overrightarrow{{}OP}$ 40 किमी, उत्तर के 30° पूर्व के विस्थापन को प्रस्तुत करती है।

2. निम्नलिखित मापदंडों को सदिश और अदिश के रूप में वर्गीकृत करें।

(i) $10 kg$

(ii) 2 मीटर उत्तर-पश्चिम

(iii) $40^{\circ}$

(iv) 40 वाट

(v) $10^{-19}$ कूलॉम

(vi) $20 m / s^{2}$

उत्तर दिखाएं

हल

(i) $10 kg$ एक अदिश राशि है क्योंकि इसमें केवल मापन होता है।

(ii) 2 मीटर उत्तर-पश्चिम एक सदिश राशि है क्योंकि इसमें मापन और दिशा दोनों होती हैं।

(iii) $40^{\circ}$ एक अदिश राशि है क्योंकि इसमें केवल मापन होता है।

(iv) 40 वाट एक अदिश राशि है क्योंकि इसमें केवल मापन होता है।

(v) $10^{-19}$ कूलॉम एक अदिश राशि है क्योंकि इसमें केवल मापन होता है।

(vi) $20 m / s^{2}$ एक सदिश राशि है क्योंकि इसमें मापन और दिशा दोनों होती हैं।

3. निम्नलिखित को अदिश और सदिश राशियों के रूप में वर्गीकृत करें।

(i) समय अवधि

(ii) दूरी

(iv) वेग

(v) कार्य किया गया

(iii) बल

उत्तर दिखाएं

हल

(i) समय अवधि एक अदिश राशि है क्योंकि इसमें केवल मापन होता है।

(ii) दूरी एक अदिश राशि है क्योंकि इसमें केवल मापन होता है।

(iii) बल एक सदिश राशि है क्योंकि इसमें मापन और दिशा दोनों होती हैं।

(iv) वेग एक सदिश राशि है क्योंकि इसमें मापन और दिशा दोनों होती हैं।

(v) कार्य किया गया एक अदिश राशि है क्योंकि इसमें केवल मापन होता है।

4. आकृति 10.6 (एक वर्ग) में निम्नलिखित सदिशों को पहचानें।

(i) सह-प्रारंभिक

(ii) समान

(iii) समान्तर लेकिन बराबर नहीं

उत्तर दिखाएँ

हल

(i) सदिश $\vec{a}$ और $\vec{d}$ समान प्रारंभ बिंदु रखते हैं कारण से वे समान प्रारंभ बिंदु रखते हैं।

(ii) सदिश $\vec{b}$ और $\vec{d}$ बराबर हैं कारण से वे समान परिमाण और दिशा रखते हैं।

(iii) सदिश $\vec{a}$ और $\vec{c}$ समान्तर लेकिन बराबर नहीं हैं। इसका कारण यह है कि यद्यपि वे समान्तर हैं, उनकी दिशाएँ एक जैसी नहीं हैं।

5. निम्नलिखित के लिए सत्य या असत्य कहें।

(i) $\vec{a}$ और $-\vec{a}$ समान्तर हैं।

(ii) दो समान्तर सदिश हमेशा समान परिमाण रखते हैं।

(iii) दो सदिशों के समान परिमाण होने पर वे समान्तर होते हैं।

चित्र 10.6

(iv) दो समान्तर सदिशों के समान परिमाण होने पर वे बराबर होते हैं।

उत्तर दिखाएँ

हल

(i) सत्य।

सदिश $\vec{a}$ और $-\vec{a}$ एक ही रेखा के समान्तर होते हैं।

(ii) असत्य।

समान्तर सदिश वे सदिश होते हैं जो एक ही रेखा के समान्तर होते हैं।

(iii) असत्य।

दो सदिशों के समान परिमाण होने पर वे समान्तर नहीं होते हैं। सदिशों के समान्तर होने के लिए वे एक ही रेखा में या एक दूसरे के समान्तर होना चाहिए।

(iv) असत्य।

दो समान्तर सदिशों के समान परिमाण होने पर वे बराबर नहीं होते हैं। सदिशों के बराबर होने के लिए वे समान परिमाण और समान दिशा रखना चाहिए।

10.4 सदिशों के योग

एक सदिश $\overrightarrow{{}AB}$ बस एक बिंदु A से बिंदु B तक के विस्थापन को दर्शाता है। अब एक लड़की के एक स्थिति में विचार करें जहां वह बिंदु A से B तक जाती है और फिर B से C तक (चित्र 10.7)। लड़की द्वारा बिंदु A से बिंदु C तक के कुल विस्थापन को सदिश $\overrightarrow{{}AC}$ द्वारा दर्शाया जाता है और इसे इस प्रकार व्यक्त किया जाता है:

$ \overrightarrow{{}AC}=\overrightarrow{{}AB}+\overrightarrow{{}BC} $

चित्र 10.7

इसे त्रिभुज नियम वेक्टर योग के रूप में जाना जाता है।

सामान्य रूप से, यदि हम दो सदिश $\vec{a}$ और $\vec{b}$ (चित्र 10.8 (i)) के साथ हैं, तो उन्हें योग करने के लिए उनकी शुरुआती बिंदु एक दूसरे के समापन बिंदु के साथ संगत कर दिया जाता है (चित्र 10.8 (ii))।

चित्र 10.8

उदाहरण के लिए, चित्र 10.8 (ii) में, हमने सदिश $\vec{b}$ के माप और दिशा को बदले बिना इसे इस तरह स्थानांतरित कर दिया है कि इसकी शुरुआती बिंदु $\vec{a}$ के समापन बिंदु के साथ संगत हो जाए। फिर, त्रिभुज ABC के तीसरे भुजा AC द्वारा प्रदर्शित सदिश $\vec{a}+\vec{b}$, सदिश $\vec{a}$ और $\vec{b}$ के योग (या परिणाम) को दर्शाता है, अर्थात त्रिभुज ABC में (चित्र 10.8 (ii)), हम निम्नलिखित प्राप्त करते हैं:

$ \overrightarrow{{}AB}+\overrightarrow{{}BC}=\overrightarrow{{}AC} $

अब फिर, क्योंकि $\overrightarrow{{}AC}=-\overrightarrow{{}CA}$, उपरोक्त समीकरण से हम निम्नलिखित प्राप्त करते हैं:

$ \overrightarrow{{}AB}+\overrightarrow{{}BC}+\overrightarrow{{}CA}=\overrightarrow{{}AA}=\overrightarrow{{}0} $

इसका अर्थ है कि जब एक त्रिभुज के भुजाएँ क्रम में ली जाती हैं, तो आरंभिक और समापन बिंदु एक दूसरे के संगत हो जाने के कारण योग का परिणाम शून्य हो जाता है (चित्र 10.8 (iii))।

अब, एक वेक्टर $\overrightarrow{{}BC^{\prime}}$ बनाएं जिसका परिमाण $\overrightarrow{{}BC}$ के समान हो, लेकिन दिशा इसके विपरीत हो (चित्र 10.8 (iii)), अर्थात,

$ \overrightarrow{{}BC^{\prime}}=-\overrightarrow{{}BC} $

फिर, चित्र 10.8 (iii) से त्रिभुज नियम के अनुसार, हमें प्राप्त होता है

$ \overrightarrow{{}AC^{\prime}}=\overrightarrow{{}AB}+\overrightarrow{{}BC^{\prime}}=\overrightarrow{{}AB}+(-\overrightarrow{{}BC})=\vec{a}-\vec{b} $

वेक्टर $\overrightarrow{{}AC^{\prime}}$ को $\vec{a}$ और $\vec{b}$ के अंतर के रूप में कहा जाता है।

अब, एक नाव के बारे में सोचें जो एक नदी के एक तट से दूसरे तट तक नदी के प्रवाह के लंबवत दिशा में जा रही है। तब, नाव को दो वेग वेक्टर लगते हैं-एक नाव के इंजन द्वारा नाव को दिया गया वेग और दूसरा नदी के पानी के प्रवाह का वेग। इन दोनों वेगों के एक साथ प्रभाव के अंतर्गत, नाव वास्तव में एक अलग वेग से यात्रा करना शुरू कर देती है। बोट के प्रभावी वेग और दिशा (अर्थात, परिणामी वेग) के बारे में एक सटीक अवधारणा के लिए, हम निम्नलिखित वेक्टर जोड़ के नियम का उपयोग करते हैं।

यदि हम दो वेक्टर $\vec{a}$ और $\vec{b}$ को एक समानांतर चतुर्भुज के दो आसन्न भुजाओं के आकार और दिशा के रूप में प्रस्तुत करते हैं (चित्र 10.9), तो उनका योग $\vec{a}+\vec{b}$ उनके सामान्य बिंदु के माध्यम से चतुर्भुज के विकर्ण द्वारा आकार और दिशा में प्रस्तुत किया जाता है। इसे समानांतर चतुर्भुज वेक्टर जोड़ का नियम कहा जाता है।

चित्र 10.9

ध्यात चित्र 10.9 से, त्रिभुज नियम का उपयोग करके, नोट किया जा सकता है कि

$\qquad \quad\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{OC}}$

या $\qquad \overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OC}}\qquad \qquad $ (क्योंकि $\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{OB}}$)

जो कि समानांतर चतुर्भुज का नियम है। अतः हम कह सकते हैं कि सदिश योग के दोनों नियम एक दूसरे के तुल्य हैं।

सदिश योग के गुण

गुण 1 किसी भी दो सदिश $\vec{a}$ और $\vec{b}$ के लिए,

$$ \qquad\vec{a}+\vec{b}=\vec{b}+\vec{a} \qquad $(संवृत्त गुण)

उपपत्ति मान लीजिए कि समानांतर चतुर्भुज $ABCD$ (चित्र 10.10) है। मान लीजिए $\overrightarrow{{}AB}=\vec{a}$ और $\overrightarrow{{}BC}=\vec{b}$, तो त्रिभुज $ABC$ के अनुसार त्रिभुज नियम का उपयोग करते हुए, हम पाते हैं:

$$ \overrightarrow{{}AC}=\vec{a}+\vec{b} $$

चित्र 10.10

अब, क्योंकि समानांतर चतुर्भुज के विपरीत भुजाएँ बराबर और समानांतर होती हैं, चित्र 10.10 से हम पाते हैं, $\overrightarrow{{}AD}=\overrightarrow{{}BC}=\vec{b}$ और $\overrightarrow{{}DC}=\overrightarrow{{}AB}=\vec{a}$. फिर त्रिभुज नियम का उपयोग करते हुए, त्रिभुज $ADC$ से हम पाते हैं:

$$ \qquad \overrightarrow{{}AC}=\overrightarrow{{}AD}+\overrightarrow{{}DC}=\vec{b}+\vec{a} $$

अतः $$ \qquad \vec{a}+\vec{b}=\vec{b}+\vec{a} $$

गुण 2 किसी तीन सदिश $a, b$ और $c$ के लिए,

$$ (\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c}) \qquad \quad $(संयोजन गुण)

उपपत्ति मान लीजिए कि सदिश $\vec{a}, \vec{b}$ और $\vec{c}$ क्रमशः चित्र 10.11 (i) और (ii) में दिखाए गए अनुसार $\overrightarrow{{}PQ}, \overrightarrow{{}QR}$ और $\overrightarrow{{}RS}$ द्वारा प्रस्तुत किए गए हैं।

चित्र 10.11

तो $\quad\quad\vec{a}+\vec{b}=\overrightarrow{{}PQ}+\overrightarrow{{}QR}=\overrightarrow{{}PR}$

और $ \quad\quad\vec{b}+\vec{c}=\overrightarrow{{}QR}+\overrightarrow{{}RS}=\overrightarrow{{}QS}$

इसलिए $ \quad\quad(\vec{a}+\vec{b})+\vec{c}=\overrightarrow{{}PR}+\overrightarrow{{}RS}=\overrightarrow{{}PS}$

और $\quad \quad\vec{a}+(\vec{b}+\vec{c})=\overrightarrow{{}PQ}+\overrightarrow{{}QS}=\overrightarrow{{}PS}$

इसलिए $\quad(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$

टिप्पणी सदिश योग के साहचर्य गुण के कारण हम तीन सदिश $\vec{a}, \vec{b}, \vec{c}$ के योग को $\vec{a}+\vec{b}+\vec{c}$ के रूप में लिख सकते हैं बिना कोष्ठक के।

ध्यान दें कि किसी भी सदिश $a$ के लिए हम निम्नलिखित के लिए रखते हैं

$ \qquad \vec{a}+\overrightarrow{{}0}=\overrightarrow{{}0}+\vec{a}=\vec{a} $

यहाँ, शून्य सदिश $\overrightarrow{{}0}$ को सदिश योग के लिए एडिटिव आइडेंटिटी कहा जाता है।

10.5 एक सदिश के स्केलर द्वारा गुणन

मान लीजिए $\vec{a}$ एक दिया गया सदिश है और $\lambda$ एक स्केलर है। तब सदिश $\vec{a}$ के स्केलर $\lambda$ द्वारा गुणन को $\lambda \vec{a}$ के रूप में नोट किया जाता है, जिसे सदिश $\vec{a}$ के स्केलर $\lambda$ द्वारा गुणन कहा जाता है। ध्यान दें कि, $\lambda \vec{a}$ एक सदिश है, जो सदिश $\vec{a}$ के समानांतर है। सदिश $\lambda \vec{a}$ की दिशा $\vec{a}$ की दिशा के समान (या विपरीत) होती है, जैसे कि $\lambda$ का मान धनात्मक (या नकारात्मक) हो। इसके अलावा, सदिश $\lambda \vec{a}$ के परिमाण $\vec{a}$ के परिमाण के $|\lambda|$ गुना होता है, अर्थात,

$ \qquad|\lambda \vec{a}|=|\lambda||\vec{a}| $

एक सदिश के स्केलर द्वारा गुणन के एक ज्यामितीय दृश्यीकरण को चित्र 10.12 में दिया गया है।

चित्र 10.12

जब $\lambda=-1$ होता है, तो $\lambda \vec{a}=-\vec{a}$, जो एक ऐसा सदिश होता है जिसका परिमाण $\vec{a}$ के परिमाण के बराबर होता है और दिशा $\vec{a}$ की दिशा के विपरीत होती है। सदिश $-\vec{a}$ को सदिश $\vec{a}$ का नकारात्मक (या एडिटिव व्युत्क्रम) कहा जाता है और हम हमेशा निम्नलिखित के लिए रखते हैं

$ \qquad \vec{a}+(-\vec{a})=(-\vec{a})+\vec{a}=\overrightarrow{{}0} $

इसके अलावा, यदि $\lambda=\dfrac{1}{|a|}$, जहाँ $\vec{a} \neq 0$ अर्थात $\vec{a}$ एक शून्य सदिश नहीं है, तो

$ \qquad \qquad|\lambda \vec{a}|=|\lambda||\vec{a}|=\dfrac{1}{|\vec{a}|}|\vec{a}|=1 $

इसलिए, $\lambda \vec{a}$ को $\vec{a}$ की दिशा में एक एकक सदिश के रूप में दर्शाया जाता है। हम इसे लिखते हैं

$ \qquad \hat{a}=\dfrac{1}{|\vec{a}|} \vec{a} $

नोट कोई भी सदिश $k, k \overrightarrow{{}0}=\overrightarrow{{}0}$ होता है।

10.5.1 सदिश के घटक

मान लीजिए बिंदु $A(1,0,0), B(0,1,0)$ और $C(0,0,1)$ क्रमशः $x$-अक्ष, $y$-अक्ष और $z$-अक्ष पर स्थित हैं। तब, स्पष्ट रूप से

$ \qquad \qquad|\overrightarrow{{}OA}|=1,|\overrightarrow{{}OB}|=1 \text{ और }|\overrightarrow{{}OC}|=1 $

सदिश $\overrightarrow{{}OA}, \overrightarrow{{}OB}$ और $\overrightarrow{{}OC}$, जिनके परिमाण 1 हैं, को अक्ष $OX, OY$ और $OZ$ के अनुदिश एक इकाई सदिश कहा जाता है और इन्हें क्रमशः $\hat{i}, \hat{j}$ और $\hat{k}$ से निरूपित किया जाता है (चित्र 10.13)।

चित्र 10.13

अब, चित्र 10.14 में दिखाए गए बिंदु $P(x, y, z)$ के स्थिति सदिश $\overline{OP}$ को विचार करें। मान लीजिए $P_1$ बिंदु $P$ से XOY तल पर लंब का पाद है।

हम इस प्रकार देखते हैं कि $P_1 P$ $z$-अक्ष के समानांतर है। चूंकि $\hat{i}, \hat{j}$ और $\hat{k}$ क्रमशः $x, y$ और $z$-अक्ष के अनुदिश इकाई सदिश हैं, और $P$ के निर्देशांक के परिभाषा के अनुसार, हमें $\overrightarrow{{}P_1 P}=\overrightarrow{{}OR}=z \hat{k}$ प्राप्त होता है। इसी तरह, $\overrightarrow{{}QP_1}=\overrightarrow{{}OS}=y \hat{j}$ और $\overrightarrow{{}OQ}=x \hat{i}$ होते हैं।

इसलिए, हम देखते हैं कि $\qquad \overrightarrow{{}OP_1}=\overrightarrow{{}OQ}+\overrightarrow{{}QP_1}=x \hat{i}+y \hat{j}$

और $\qquad \qquad \qquad \quad \qquad \quad\overrightarrow{{}OP}=\overrightarrow{{}OP_1}+\overrightarrow{{}P_1 P}=x \hat{i}+y \hat{j}+z \hat{k}$

इसलिए, $O$ के संदर्भ में $P$ के स्थिति सदिश को निम्नलिखित द्वारा दिया जाता है

$ \qquad \qquad \qquad\overrightarrow{{}OP}(\text{ या } \vec{r})=x \hat{i}+y \hat{j}+z \hat{k} $

$

इस प्रकार के किसी भी सदिश के रूप को इसके कंपोनेंट रूप कहा जाता है। यहाँ, $x, y$ और $z$ को $\vec{r}$ के скаलर कंपोनेंट कहा जाता है, और $x \hat{i}, y \hat{j}$ और $z \hat{k}$ को $\vec{r}$ के वेक्टर कंपोनेंट कहा जाता है, जो क्रमशः अक्षों के अनुदिश होते हैं। कभी-कभी $x, y$ और $z$ को भी आयताकार कंपोनेंट कहा जाता है।

किसी भी सदिश $\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$ की लंबाई को एक बार में पिथागोरस प्रमेय के उपयोग द्वारा आसानी से निर्धारित किया जा सकता है। हम ध्यान देते हैं कि दाहिने कोण के त्रिकोण $OQP_1$ (चित्र 10.14)

$ \qquad \qquad \qquad|\overrightarrow{{}OP_1}|=\sqrt{|\overrightarrow{{}OQ}|^{2}+|\overrightarrow{{}QP_1}|^{2}}=\sqrt{x^{2}+y^{2}}, $

और दाहिने कोण के त्रिकोण $OP_1 P$ में हम निम्नलिखित प्राप्त करते हैं:

$ \qquad \qquad \qquad\overrightarrow{{}OP}=\sqrt{|\overrightarrow{{}OP_1}|^{2}+|\overrightarrow{{}P_1 P}|^{2}}=\sqrt{(x^{2}+y^{2})+z^{2}} $

इसलिए, किसी भी सदिश $\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$ की लंबाई निम्नलिखित द्वारा दी जाती है:

$ \qquad \qquad \qquad|\vec{r}|=|x \hat{i}+y \hat{j}+z \hat{k}|=\sqrt{x^{2}+y^{2}+z^{2}} $

यदि $\vec{a}$ और $\vec{b}$ कोई दो सदिश हैं जो कंपोनेंट रूप में $a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ और $b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$ के रूप में दिए गए हैं, तो

(i) सदिश $\vec{a}$ और $\vec{b}$ के योग (या परिणाम) निम्नलिखित द्वारा दिया जाता है:

$ \qquad \qquad \qquad \vec{a}+\vec{b}=(a_1+b_1) \hat{i}+(a_2+b_2) \hat{j}+(a_3+b_3) \hat{k} $

(ii) सदिश $\vec{a}$ और $\vec{b}$ के अंतर निम्नलिखित द्वारा दिया जाता है:

$ \qquad \qquad \qquad \vec{a}-\vec{b}=(a_1-b_1) \hat{i}+(a_2-b_2) \hat{j}+(a_3-b_3) \hat{k} $

(iii) सदिश $\vec{a}$ और $\vec{b}$ बराबर होते हैं यदि और केवल यदि

$ \qquad \qquad \qquad a_1=b_1, a_2=b_2 \quad \text{ और } \quad a_3=b_3 $

(iv) सदिश $\vec{a}$ को कोई भी अदिश $\lambda$ से गुणा करने पर निम्नलिखित द्वारा दिया जाता है:

$ \qquad \qquad \qquad \lambda \vec{a}=(\lambda a_1) \hat{i}+(\lambda a_2) \hat{j}+(\lambda a_3) \hat{k} $

सदिशों के योग और एक सदिश को एक अदिश से गुणा करने के संयोजन निम्नलिखित वितरण नियमों को देते हैं:

मान लीजिए $\vec{a}$ और $\vec{b}$ कोई दो सदिश हैं, और $k$ और $m$ कोई भी अदिश हैं। तब

(i) $k \vec{a}+m \vec{a}=(k+m) \vec{a}$

(ii) $k(m \vec{a})=(k m) \vec{a}$

(iii) $k(\vec{a}+\vec{b})=k \vec{a}+k \vec{b}$

टिप्पणियाँ

(i) एक देख सकते हैं कि चाहे $\lambda$ का मान क्या हो, वेक्टर $\lambda \vec{a}$ हमेशा वेक्टर $\vec{a}$ के समानुपाती होता है। वास्तव में, दो वेक्टर $\vec{a}$ और $\vec{b}$ समानुपाती होते हैं यदि और केवल यदि एक गैर-शून्य अदिश $\lambda$ के लिए $\vec{b}=\lambda \vec{a}$ हो। यदि वेक्टर $\vec{a}$ और $\vec{b}$ घटक रूप में दिए गए हों, अर्थात $\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ और $\vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$, तो दो वेक्टर समानुपाती होते हैं यदि और केवल यदि

$ \qquad \qquad \qquad\begin{array}{cc} & b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}=\lambda\left(a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}\right) \\ \Leftrightarrow & b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}=\left(\lambda a_1\right) \hat{i}+\left(\lambda a_2\right) \hat{j}+\left(\lambda a_3\right) \hat{k} \\ \Leftrightarrow & b_1=\lambda a_1, b_2=\lambda a_2, b_3=\lambda a_3 \\ \Leftrightarrow & \dfrac{b_1}{a_1}=\dfrac{b_2}{a_2}=\dfrac{b_3}{a_3}=\lambda \end{array} $

(ii) यदि $\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$, तो $a_1, a_2, a_3$ को $\vec{a}$ के दिशा अनुपात भी कहा जाता है।

(iii) यदि दिया गया हो कि $l, m, n$ एक वेक्टर के दिशा कोसाइन हैं, तो $l \hat{i}+m \hat{j}+n \hat{k}$ $=(\cos \alpha) \hat{i}+(\cos \beta) \hat{j}+(\cos \gamma) \hat{k}$ उस वेक्टर की दिशा में एक इकाई वेक्टर होता है, जहाँ $\alpha, \beta$ और $\gamma$ वेक्टर क्रमशः $x, y$ और $z$ अक्षों के साथ बनाए गए कोण हैं।

उदाहरण 4 ऐसे मान ज्ञात कीजिए कि वेक्टर $\vec{a}=x \hat{i}+2 \hat{j}+z \hat{k}$ और $\vec{b}=2 \hat{i}+y \hat{j}+\hat{k}$ समान हों।

हल ध्यान दें कि दो वेक्टर समान होते हैं यदि और केवल यदि उनके संगत घटक समान हों। अतः दिए गए वेक्टर $\vec{a}$ और $\vec{b}$ समान होंगे यदि और केवल यदि

$ \qquad x=2, y=2, z=1 $

उदाहरण 5 मान लीजिए $\vec{a}=\hat{i}+2 \hat{j}$ और $\vec{b}=2 \hat{i}+\hat{j}$. क्या $|\vec{a}|=|\vec{b}|$ ? क्या वेक्टर $\vec{a}$ और $\vec{b}$ समान हैं?

हल हमें $|\vec{a}|=\sqrt{1^{2}+2^{2}}=\sqrt{5}$ और $|\vec{b}|=\sqrt{2^{2}+1^{2}}=\sqrt{5}$ मिलता है

इसलिए, $|\vec{a}|=|\vec{b}|$। लेकिन, दोनों वेक्टर बराबर नहीं हैं क्योंकि उनके संगत घटक अलग-अलग हैं।

उदाहरण 6 वेक्टर $\vec{a}=2 \hat{i}+3 \hat{j}+\hat{k}$ की दिशा में एक एकक वेक्टर ज्ञात कीजिए।

हल वेक्टर $\vec{a}$ की दिशा में एक एकक वेक्टर $\hat{a}$ निम्नलिखित द्वारा दिया जाता है: $\hat{a}=\dfrac{1}{|\vec{a}|} \vec{a}$।

अब $ \qquad \qquad \qquad|\vec{a}|=\sqrt{2^{2}+3^{2}+1^{2}}=\sqrt{14} $

इसलिए $ \qquad \qquad \quad \hat{a}=\dfrac{1}{\sqrt{14}}(2 \hat{i}+3 \hat{j}+\hat{k})=\dfrac{2}{\sqrt{14}} \hat{i}+\dfrac{3}{\sqrt{14}} \hat{j}+\dfrac{1}{\sqrt{14}} \hat{k} $

उदाहरण 7 वेक्टर $\vec{a}=\hat{i}-2 \hat{j}$ की दिशा में एक वेक्टर ज्ञात कीजिए जिसका माप 7 इकाई हो।

हल दिए गए वेक्टर $\vec{a}$ की दिशा में एकक वेक्टर है

$ \qquad \qquad \qquad \hat{a}=\dfrac{1}{|\vec{a}|} \vec{a}=\dfrac{1}{\sqrt{5}}(\hat{i}-2 \hat{j})=\dfrac{1}{\sqrt{5}} \hat{i}-\dfrac{2}{\sqrt{5}} \hat{j} $

इसलिए, वह वेक्टर जिसका माप 7 इकाई है और जो $\vec{a}$ की दिशा में है, है

$ \qquad \qquad \qquad 7 \hat{a}=7\left(\dfrac{1}{\sqrt{5}} \hat{i}-\dfrac{2}{\sqrt{5}} \hat{j}\right)=\dfrac{7}{\sqrt{5}} \hat{i}-\dfrac{14}{\sqrt{5}} \hat{j} $

उदाहरण 8 वेक्टर $\vec{a}=2 \hat{i}+2 \hat{j}-5 \hat{k}$ और $\vec{b}=2 \hat{i}+\hat{j}+3 \hat{k}$ के योग की दिशा में एक एकक वेक्टर ज्ञात कीजिए।

हल दिए गए वेक्टरों का योग है

$ \qquad \qquad \qquad \vec{a}+\vec{b}(=\vec{c}, \text{ मान लीजिए })=4 \hat{i}+3 \hat{j}-2 \hat{k} $

और $\qquad \qquad \qquad|\vec{c}|=\sqrt{4^{2}+3^{2}+(-2)^{2}}=\sqrt{29}$

इसलिए, आवश्यक एकक वेक्टर है

$ \qquad \qquad \qquad \hat{c}=\dfrac{1}{|\vec{c}|} \vec{c}=\dfrac{1}{\sqrt{29}}(4 \hat{i}+3 \hat{j}-2 \hat{k})=\dfrac{4}{\sqrt{29}} \hat{i}+\dfrac{3}{\sqrt{29}} \hat{j}-\dfrac{2}{\sqrt{29}} \hat{k} $

उदाहरण 9 वेक्टर $\vec{a}=\hat{i}+\hat{j}-2 \hat{k}$ के दिशा अनुपात लिखिए और फिर इसके दिशा कोसाइन गणना कीजिए।

हल ध्यान दें कि सदिश $\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$ के दिशा अनुपात $a, b, c$ केवल सदिश के संगत घटक $x, y$ और $z$ होते हैं। अतः दिए गए सदिश के लिए हमें $a=1, b=1$ और $c=-2$ मिलते हैं। इसके अतिरिक्त, यदि $l, m$ और $n$ दिए गए सदिश के दिशा कोसाइन हों, तो

$ \qquad \qquad \qquad 1=\dfrac{a}{|\vec{r}|}=\dfrac{1}{\sqrt{6}}, \quad m=\dfrac{b}{|\vec{r}|}=\dfrac{1}{\sqrt{6}}, \quad n=\dfrac{c}{|\vec{r}|}=\dfrac{-2}{\sqrt{6}} \text{ क्योंकि }|\vec{r}|=\sqrt{6} $

इसलिए, दिशा कोसाइन हैं $\left(\dfrac{1}{\sqrt{6}}, \dfrac{1}{\sqrt{6}},-\dfrac{2}{\sqrt{6}}\right)$।

10.5.2 दो बिंदुओं को मिलाने वाला सदिश

यदि $P_1(x_1, y_1, z_1)$ और $P_2(x_2, y_2, z_2)$ कोई दो बिंदु हों, तो $P_1$ और $P_2$ को मिलाने वाला सदिश सदिश $\overrightarrow{{}P_1} _2$ (चित्र 10.15) होता है।

बिंदुओं $P_1$ और $P_2$ को मूल बिंदु $O$ से जोड़कर त्रिभुज के नियम को लागू करते हुए, त्रिभुज $OP_1 P_2$ से हमें प्राप्त होता है

$ \qquad \qquad \qquad \overrightarrow{{}OP_1}+\overrightarrow{{}P_1} _2=\overrightarrow{{}OP_2} $

चित्र 10.15

सदिश जोड़ के गुणों का उपयोग करते हुए, उपरोक्त समीकरण बन जाता है

$ \text{ अर्थात } \qquad \qquad \qquad \begin{aligned} \overrightarrow{{}P_1} _2 & =\overrightarrow{{}OP_2}-\overrightarrow{{}OP_1} \\ \overrightarrow{{}P_1} _2 & =(x_2 \hat{i}+y_2 \hat{j}+z_2 \hat{k})-(x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k}) \\ & =(x_2-x_1) \hat{i}+(y_2-y_1) \hat{j}+(z_2-z_1) \hat{k} \end{aligned} $

सदिश $\overrightarrow{{}P_1} _2$ के परिमाण को निम्नलिखित द्वारा दिया जाता है

$ \qquad \qquad \qquad \quad|\overrightarrow{{}P_1} _2|=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}} $

उदाहरण 10 बिंदुओं $P(2,3,0)$ और $Q(-1,-2,-4)$ को मिलाने वाले सदिश को ज्ञात कीजिए जो $P$ से $Q$ की ओर दिशा में हो।

हल चूंकि सदिश $P$ से $Q$ की ओर दिशा में होना चाहिए, अतः स्पष्ट रूप से $P$ शुरुआती बिंदु है और $Q$ समापन बिंदु है। अतः $P$ और $Q$ को मिलाने वाले आवश्यक सदिश को $P$ और $Q$ के बीच बनाया गया सदिश $\overrightarrow{{}PQ}$ होता है, जो निम्नलिखित द्वारा दिया जाता है

हल ध्यान दें कि सदिश $\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$ के दिशा अनुपात $a, b, c$ केवल सदिश के संगत घटक $x, y$ और $z$ होते हैं। अतः दिए गए सदिश के लिए हमें $a=1, b=1$ और $c=-2$ मिलते हैं। इसके अतिरिक्त, यदि $l, m$ और $n$ दिए गए सदिश के दिशा कोसाइन हों, तो

$ \qquad \qquad \qquad 1=\dfrac{a}{|\vec{r}|}=\dfrac{1}{\sqrt{6}}, \quad m=\dfrac{b}{|\vec{r}|}=\dfrac{1}{\sqrt{6}}, \quad n=\dfrac{c}{|\vec{r}|}=\dfrac{-2}{\sqrt{6}} \text{ क्योंकि }|\vec{r}|=\sqrt{6} $

इसलिए, दिशा कोसाइन हैं $\left(\dfrac{1}{\sqrt{6}}, \dfrac{1}{\sqrt{6}},-\dfrac{2}{\sqrt{6}}\right)$।

10.5.2 दो बिंदुओं को मिलाने वाला सदिश

यदि $P_1(x_1, y_1, z_1)$ और $P_2(x_2, y_2, z_2)$ कोई दो बिंदु हों, तो $P_1$ और $P_2$ को मिलाने वाला सदिश सदिश $\overrightarrow{{}P_1} _2$ (चित्र 10.15) होता है।

बिंदुओं $P_1$ और $P_2$ को मूल बिंदु $O$ से जोड़कर त्रिभुज के नियम को लागू करते हुए, त्रिभुज $OP_1 P_2$ से हमें प्राप्त होता है

$ \qquad \qquad \qquad \overrightarrow{{}OP_1}+\overrightarrow{{}P_1} _2=\overrightarrow{{}OP_2} $

चित्र 10.15

सदिश जोड़ के गुणों का उपयोग करते हुए, उपरोक्त समीकरण बन जाता है

$ \text{ अर्थात } \qquad \qquad \qquad \begin{aligned} \overrightarrow{{}P_1} _2 & =\overrightarrow{{}OP_2}-\overrightarrow{{}OP_1} \\ \overrightarrow{{}P_1} _2 & =(x_2 \hat{i}+y_2 \hat{j}+z_2 \hat{k})-(x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k}) \\ & =(x_2-x_1) \hat{i}+(y_2-y_1) \hat{j}+(z_2-z_1) \hat{k} \end{aligned} $

सदिश $\overrightarrow{{}P_1} _2$ के परिमाण को निम्नलिखित द्वारा दिया जाता है

$ \qquad \qquad \qquad \quad|\overrightarrow{{}P_1} _2|=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}} $

उदाहरण 10 बिंदुओं $P(2,3,0)$ और $Q(-1,-2,-4)$ को मिलाने वाले सदिश को ज्ञात कीजिए जो $P$ से $Q$ की ओर दिशा में हो।

हल चूंकि सदिश $P$ से $Q$ की ओर दिशा में होना चाहिए, अतः स्पष्ट रूप से $P$ शुरुआती बिंदु है और $Q$ समापन बिंदु है। अतः $P$ और $Q$ को मिलाने वाले आवश्यक सदिश को $P$ और $Q$ के बीच बनाया गया सदिश $\overrightarrow{{}PQ}$ होता है, जो निम्नलिखित द्वारा दिया जाता है

$ \begin{aligned} & \overrightarrow{{}PQ}=(-1-2) \hat{i}+(-2-3) \hat{j}+(-4-0) \hat{k} \\ \text { अर्थात } \qquad \qquad \qquad & \overrightarrow{{}PQ}=-3 \hat{i}-5 \hat{j}-4 \hat{k} \end{aligned} $

10.5.3 खंड सूत्र

मान लीजिए $P$ और $Q$ दो बिंदु हैं जो मूल बिंदु $O$ के संदर्भ में स्थिति सदिश $\overrightarrow{{}OP}$ और $\overrightarrow{{}OQ}$ द्वारा प्रस्तुत किए जाते हैं। तब बिंदुओं $P$ और $Q$ को जोड़ने वाले रेखाखंड को एक तीसरे बिंदु, मान लीजिए $R$, दो तरीकों से विभाजित कर सकता है - आंतरिक रूप से (चित्र 10.16) और बाहरी रूप से (चित्र 10.17)। यहाँ हम बिंदु $R$ के संदर्भ में स्थिति सदिश $\overrightarrow{{}OR}$ को खोजना चाहते हैं। हम दोनों मामलों को एक एक करके लेते हैं।

चित्र 10.16

मामला I जब $R$ बिंदुओं $PQ$ को आंतरिक रूप से विभाजित करता है (चित्र 10.16)। यदि $R$ ऐसे विभाजित करता है कि $m \overrightarrow{{}RQ}=n \overrightarrow{{}PR}$,

जहाँ $m$ और $n$ धनात्मक अदिश हैं, तो हम कहते हैं कि बिंदु $R$ बिंदुओं $PQ$ को $m:n$ के अनुपात में आंतरिक रूप से विभाजित करता है। अब त्रिभुज ORQ और OPR से हम निम्नलिखित प्राप्त करते हैं

$ \qquad \qquad \qquad \overrightarrow{{}RQ}=\overrightarrow{{}OQ}-\overrightarrow{{}OR}=\vec{b}-\vec{r} $

और $ \qquad \qquad \overrightarrow{{}PR}=\overrightarrow{{}OR}-\overrightarrow{{}OP}=\vec{r}-\vec{a} $

इसलिए, हम निम्नलिखित प्राप्त करते हैं $\qquad \qquad m(\vec{b}-\vec{r}) =n(\vec{r}-\vec{a}) \quad \text{ (क्यों?) }$

या $ \qquad \qquad \qquad \qquad\qquad \vec{r} =\dfrac{m \vec{b}+n \vec{a}}{m+n} \qquad \text{ (सरलीकरण करने पर) }$

इसलिए, बिंदुओं $P$ और $Q$ को $m:n$ के अनुपात में आंतरिक रूप से विभाजित करने वाले बिंदु $R$ के संदर्भ में स्थिति सदिश $\overrightarrow{{}OR}$ निम्नलिखित है

$ \qquad \qquad \qquad \overrightarrow{{}OR}=\dfrac{m \vec{b}+n \vec{a}}{m+n} $

मामला II जब $R$ बिंदुओं $PQ$ को बाहरी रूप से विभाजित करता है (चित्र 10.17)। हम इसे पाठक के अभ्यास के रूप में छोड़ देते हैं जांच करे कि बिंदुओं $PQ$ को $m:n$ के अनुपात में बाहरी रूप से विभाजित करने वाले बिंदु $R$ के संदर्भ में स्थिति सदिश $\dfrac{PR}{QR}=\dfrac{m}{n}$ द्वारा दिया जाता है

$ \qquad \qquad \qquad \overrightarrow{{}OR}=\dfrac{m \vec{b}-n \vec{a}}{m-n} $

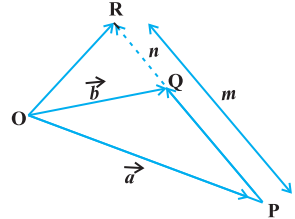
चित्र 10.17

टिप्पणी यदि $R$, $PQ$ का मध्य बिंदु है, तो $m=n$ होगा। और इसलिए, मामला I से, $PQ$ के मध्य बिंदु $R$ का स्थिति सदिश निम्नलिखित होगा

$ \qquad \qquad \qquad \overrightarrow{{}OR}=\dfrac{\vec{a}+\vec{b}}{2} $

उदाहरण 11 दो बिंदुओं $P$ और $Q$ के स्थिति सदिश $\overrightarrow{{}OP}=3 \vec{a}-2 \vec{b}$ और $\overrightarrow{{}OQ}=\vec{a}+\vec{b}$ हैं। एक बिंदु $R$ के स्थिति सदिश ज्ञात कीजिए जो $P$ और $Q$ को मिलाने वाली रेखा को $2: 1$ के अनुपात में विभाजित करता है, (i) आंतरिक रूप से, और (ii) बाहरी रूप से।

हल

(i) $P$ और $Q$ के मिलाने वाली रेखा के आंतरिक रूप से $2: 1$ के अनुपात में विभाजित करने वाले बिंदु $R$ का स्थिति सदिश निम्नलिखित है

$ \qquad \qquad \qquad \overrightarrow{{}OR}=\dfrac{2(\vec{a}+\vec{b})+(3 \vec{a}-2 \vec{b})}{2+1}=\dfrac{5 \vec{a}}{3} $

(ii) $P$ और $Q$ के मिलाने वाली रेखा के बाहरी रूप से $2: 1$ के अनुपात में विभाजित करने वाले बिंदु $R$ का स्थिति सदिश निम्नलिखित है

$ \qquad \qquad \qquad \overrightarrow{{}OR}=\dfrac{2(\vec{a}+\vec{b})-(3 \vec{a}-2 \vec{b})}{2-1}=4 \vec{b}-\vec{a} $

उदाहरण 12 सिद्ध कीजिए कि बिंदु $A(2 \hat{i}-\hat{j}+\hat{k}), B(\hat{i}-3 \hat{j}-5 \hat{k}), C(3 \hat{i}-4 j-4 \hat{k})$ एक समकोण त्रिभुज के शीर्ष हैं।

हल हम जानते हैं कि

$ \qquad \qquad \qquad \begin{aligned} & \overrightarrow{{}AB}=(1-2) \hat{i}+(-3+1) \hat{j}+(-5-1) \hat{k}=-\hat{i}-2 \hat{j}-6 \hat{k} \\ & \overrightarrow{{}BC}=(3-1) \hat{i}+(-4+3) \hat{j}+(-4+5) \hat{k}=2 \hat{i}-\hat{j}+\hat{k} \end{aligned} $

और $ \qquad \qquad \overrightarrow{{}CA}=(2-3) \hat{i}+(-1+4) \hat{j}+(1+4) \hat{k}=-\hat{i}+3 \hat{j}+5 \hat{k} $

इसके अतिरिक्त, ध्यान दें कि

$ \qquad \qquad \qquad |\overrightarrow{{}AB}|^{2}=41=6+35=|\overrightarrow{{}BC}|^{2}+|\overrightarrow{{}CA}|^{2} $

इसलिए, त्रिभुज एक समकोण त्रिभुज है।

अभ्यास 10.2

1. निम्नलिखित सदिशों के परिमाण की गणना कीजिए:

$$ \vec{a}=\hat{i}+\hat{j}+k ; \quad \vec{b}=2 \hat{i}-7 \hat{j}-3 \hat{k} ; \quad \vec{c}=\dfrac{1}{\sqrt{3}} \hat{i}+\dfrac{1}{\sqrt{3}} \hat{j}-\dfrac{1}{\sqrt{3}} \hat{k} $$

उत्तर दिखाएं

हल

दिए गए सदिश हैं:

$ \begin{aligned} \vec{a} & =\hat{i}+\hat{j}+\hat{k} ; \quad \vec{b}=2 \hat{i}-7 \hat{j}-3 \hat{k} ; \quad \vec{c}=\dfrac{1}{\sqrt{3}} \hat{i}+\dfrac{1}{\sqrt{3}} \hat{j}-\dfrac{1}{\sqrt{3}} \hat{k} \\ |\vec{a}| & =\sqrt{(1)^{2}+(1)^{2}+(1)^{2}}=\sqrt{3} \\ |\vec{b}| & =\sqrt{(2)^{2}+(-7)^{2}+(-3)^{2}} \\ & =\sqrt{4+49+9} \\ & =\sqrt{62} \\ |\vec{c}| & =\sqrt{(\dfrac{1}{\sqrt{3}})^{2}+(\dfrac{1}{\sqrt{3}})^{2}+(-\dfrac{1}{\sqrt{3}})^{2}} \\ & =\sqrt{\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}}=1 \end{aligned} $

2. दो अलग-अलग सदिश लिखिए जो समान परिमाण रखते हों।

उत्तर दिखाएं

हल

मान लीजिए $\vec{a}=(\hat{i}-2 \hat{j}+3 \hat{k})$ और $\vec{b}=(2 \hat{i}+\hat{j}-3 \hat{k})$।

यह देखा जा सकता है कि $|\vec{a}|=\sqrt{1^{2}+(-2)^{2}+3^{2}}=\sqrt{1+4+9}=\sqrt{14}$ और $|\vec{b}|=\sqrt{2^{2}+1^{2}+(-3)^{2}}=\sqrt{4+1+9}=\sqrt{14}$।

अतः, $\vec{a}$ और $\vec{b}$ दो अलग-अलग सदिश हैं जो समान परिमाण रखते हैं। इन सदिशों के अलग-अलग दिशा होने के कारण वे अलग-अलग हैं।

3. दो अलग-अलग सदिश लिखिए जो समान दिशा रखते हों।

उत्तर दिखाएं

हल

मान लीजिए $\vec{p}=(\hat{i}+\hat{j}+\hat{k})$ और $\vec{q}=(2 \hat{i}+2 \hat{j}+2 \hat{k})$।

$\vec{p}$ के दिशा कोसाइन निम्नलिखित हैं,

$l=\dfrac{1}{\sqrt{1^{2}+1^{2}+1^{2}}}=\dfrac{1}{\sqrt{3}}, m=\dfrac{1}{\sqrt{1^{2}+1^{2}+1^{2}}}=\dfrac{1}{\sqrt{3}}$, और $n=\dfrac{1}{\sqrt{1^{2}+1^{2}+1^{2}}}=\dfrac{1}{\sqrt{3}}$।

$\vec{q}$ के दिशा कोसाइन निम्नलिखित हैं

$l=\dfrac{2}{\sqrt{2^{2}+2^{2}+2^{2}}}=\dfrac{2}{2 \sqrt{3}}=\dfrac{1}{\sqrt{3}}, m=\dfrac{2}{\sqrt{2^{2}+2^{2}+2^{2}}}=\dfrac{2}{2 \sqrt{3}}=\dfrac{1}{\sqrt{3}}$,

और $n=\dfrac{2}{\sqrt{2^{2}+2^{2}+2^{2}}}=\dfrac{2}{2 \sqrt{3}}=\dfrac{1}{\sqrt{3}}$.

$\vec{p}$ और $\vec{q}$ के दिशा कोसाइन समान हैं। इसलिए, दोनों सदिश एक ही दिशा में हैं।

4. $2 \hat{i}+3 \hat{j}$ और $x \hat{i}+y \hat{j}$ बराबर सदिश हों तो $x$ और $y$ के मान ज्ञात कीजिए।

उत्तर दिखाएं

हल

$2 \hat{i}+3 \hat{j}$ और $x \hat{i}+y \hat{j}$ बराबर होंगे यदि उनके संगत घटक बराबर हों।

इसलिए, $x$ और $y$ के आवश्यक मान क्रमशः 2 और 3 हैं।

5. आरंभिक बिंदु $(2,1)$ और समापन बिंदु $(-5,7)$ वाले सदिश के अदिश और सदिश घटक ज्ञात कीजिए।

उत्तर दिखाएं

हल

आरंभिक बिंदु $P(2,1)$ और समापन बिंदु $Q(-5,7)$ वाले सदिश को, $\overrightarrow{{}PQ}=(-5-2) \hat{i}+(7-1) \hat{j}$ द्वारा दिया जा सकता है।

$\Rightarrow \overrightarrow{{}PQ}=-7 \hat{i}+6 \hat{j}$

इसलिए, आवश्यक अदिश घटक -7 और 6 हैं जबकि सदिश घटक $-7 \hat{i}$ और $6 \hat{j}$ हैं।

6. सदिश $\vec{a}=\hat{i}-2 \hat{j}+\hat{k}, \vec{b}=-2 \hat{i}+4 \hat{j}+5 \hat{k}$ और $\vec{c}=\hat{i}-6 \hat{j}-7 \hat{k}$ के योग ज्ञात कीजिए।

उत्तर दिखाएं

हल

दिए गए सदिश $\vec{a}=\hat{i}-2 \hat{j}+\hat{k}, \vec{b}=-2 \hat{i}+4 \hat{j}+5 \hat{k}$ और $\vec{c}=\hat{i}-6 \hat{j}-7 \hat{k}$ हैं।

$ \begin{aligned} \therefore \vec{a}+\vec{b}+\vec{c} & =(1-2+1) \hat{i}+(-2+4-6) \hat{j}+(1+5-7) \hat{k} \\ & =0 \cdot \hat{i}-4 \hat{j}-1 \cdot \hat{k} \\ & =-4 \hat{j}-\hat{k} \end{aligned} $

7. सदिश $\vec{a}=\hat{i}+\hat{j}+2 \hat{k}$ की दिशा में एक एकक सदिश ज्ञात कीजिए।

उत्तर दिखाएं

हल

सदिश $\vec{a}=\hat{i}+\hat{j}+2 \hat{k}$ की दिशा में एक एकक सदिश $\hat{a}$ निम्नलिखित द्वारा दिया जाता है: $\hat{a}=\dfrac{\vec{a}}{|a|}$।

$|\vec{a}|=\sqrt{1^{2}+1^{2}+2^{2}}=\sqrt{1+1+4}=\sqrt{6}$

$\therefore \hat{a}=\dfrac{\vec{a}}{|\vec{a}|}=\dfrac{\hat{i}+\hat{j}+2 \hat{k}}{\sqrt{6}}=\dfrac{1}{\sqrt{6}} \hat{i}+\dfrac{1}{\sqrt{6}} \hat{j}+\dfrac{2}{\sqrt{6}} \hat{k}$

8. सदिश $\overrightarrow{{}PQ}$ की दिशा में एक एकक सदिश ज्ञात कीजिए, जहाँ $P$ और $Q$ क्रमशः $(1,2,3)$ और $(4,5,6)$ बिंदु हैं।

उत्तर दिखाएँ

हल

दिए गए बिंदु $P(1,2,3)$ और $Q(4,5,6)$ हैं।

$ \begin{aligned} & \therefore \overrightarrow{{}PQ}=(4-1) \hat{i}+(5-2) \hat{j}+(6-3) \hat{k}=3 \hat{i}+3 \hat{j}+3 \hat{k} \\ & |\overrightarrow{{}PQ}|=\sqrt{3^{2}+3^{2}+3^{2}}=\sqrt{9+9+9}=\sqrt{27}=3 \sqrt{3} \end{aligned} $

इसलिए, $\overrightarrow{{}PQ}$ की दिशा में एक एकक सदिश है

$ \dfrac{\overrightarrow{{}PQ}}{|\overrightarrow{{}PQ}|}=\dfrac{3 \hat{i}+3 \hat{j}+3 \hat{k}}{3 \sqrt{3}}=\dfrac{1}{\sqrt{3}} \hat{i}+\dfrac{1}{\sqrt{3}} \hat{j}+\dfrac{1}{\sqrt{3}} \hat{k} $

9. दिए गए सदिशों, $\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}$ और $\vec{b}=-\hat{i}+\hat{j}-\hat{k}$ के लिए, सदिश $\vec{a}+\vec{b}$ की दिशा में एक एकक सदिश ज्ञात कीजिए।

उत्तर दिखाएँ

हल

दिए गए सदिश $\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}$ और $\vec{b}=-\hat{i}+\hat{j}-\hat{k}$ हैं।

$\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}$

$\vec{b}=-\hat{i}+\hat{j}-\hat{k}$

$\therefore \vec{a}+\vec{b}=(2-1) \hat{i}+(-1+1) \hat{j}+(2-1) \hat{k}=1 \hat{i}+0 \hat{j}+1 \hat{k}=\hat{i}+\hat{k}$

$|\vec{a}+\vec{b}|=\sqrt{1^{2}+1^{2}}=\sqrt{2}$

इसलिए, $(\vec{a}+\vec{b})$ की दिशा में एक एकक सदिश है

$\dfrac{(\vec{a}+\vec{b})}{|\vec{a}+\vec{b}|}=\dfrac{\hat{i}+\hat{k}}{\sqrt{2}}=\dfrac{1}{\sqrt{2}} \hat{i}+\dfrac{1}{\sqrt{2}} \hat{k}$

10. सदिश $5 \hat{i}-\hat{j}+2 \hat{k}$ की दिशा में एक सदिश ज्ञात कीजिए जो 8 इकाई के माप का हो।

उत्तर दिखाएँ

हल

मान लीजिए $\vec{a}=5 \hat{i}-\hat{j}+2 \hat{k}$।

$\therefore|\vec{a}|=\sqrt{5^{2}+(-1)^{2}+2^{2}}=\sqrt{25+1+4}=\sqrt{30}$

$\therefore \hat{a}=\dfrac{\vec{a}}{|\vec{a}|}=\dfrac{5 \hat{i}-\hat{j}+2 \hat{k}}{\sqrt{30}}$

इसलिए, सदिश $5 \hat{i}-\hat{j}+2 \hat{k}$ की दिशा में जो 8 इकाई के माप का हो वह निम्नलिखित द्वारा दिया जाता है,

हल

मान लीजिए $\vec{a}=5 \hat{i}-\hat{j}+2 \hat{k}$।

$\therefore|\vec{a}|=\sqrt{5^{2}+(-1)^{2}+2^{2}}=\sqrt{25+1+4}=\sqrt{30}$

$\therefore \hat{a}=\dfrac{\vec{a}}{|\vec{a}|}=\dfrac{5 \hat{i}-\hat{j}+2 \hat{k}}{\sqrt{30}}$

इसलिए, सदिश $5 \hat{i}-\hat{j}+2 \hat{k}$ की दिशा में जो 8 इकाई के माप का हो वह निम्नलिखित द्वारा दिया जाता है,

8 \hat{a} = 8 \times \dfrac{5 \hat{i}-\hat{j}+2 \hat{k}}{\sqrt{30}} = \dfrac{8}{\sqrt{30}} (5 \hat{i}-\hat{j}+2 \hat{k})

$8 \hat{a}=8(\dfrac{5 \hat{i}-\hat{j}+2 \hat{k}}{\sqrt{30}})$

$ \begin{aligned} & =8(\dfrac{5 \vec{i}-\vec{j}+2 \vec{k}}{\sqrt{30}}) \\ & =\dfrac{40}{\sqrt{30}} \vec{i}-\dfrac{8}{\sqrt{30}} \vec{j}+\dfrac{16}{\sqrt{30}} \vec{k} \end{aligned} $

11. सिद्ध कीजिए कि सदिश $2 \hat{i}-3 \hat{j}+4 \hat{k}$ और $-4 \hat{i}+6 \hat{j}-8 \hat{k}$ संरेख हैं।

उत्तर दिखाएं

हल

मान लीजिए $\vec{a}=2 \hat{i}-3 \hat{j}+4 \hat{k}$ और $\vec{b}=-4 \hat{i}+6 \hat{j}-8 \hat{k}$।

यह देखा जा सकता है कि $\vec{b}=-4 \hat{i}+6 \hat{j}-8 \hat{k}=-2(2 \hat{i}-3 \hat{j}+4 \hat{k})=-2 \vec{a}$

$\therefore \vec{b}=\lambda \vec{a}$

जहाँ,

$\lambda=-2$

अतः, दिए गए सदिश संरेख हैं।

12. सदिश $\hat{i}+2 \hat{j}+3 \hat{k}$ के दिशा कोसाइन ज्ञात कीजिए।

उत्तर दिखाएं

हल

मान लीजिए $\vec{a}=\hat{i}+2 \hat{j}+3 \hat{k}$।

दिशा अनुपात :

$a=1, b=2, c=3$

$\therefore|\vec{a}|=\sqrt{1^{2}+2^{2}+3^{2}}=\sqrt{1+4+9}=\sqrt{14}$

दिशा कोसाइन :

$(\dfrac{a}{|\vec a|},\dfrac{b}{|\vec a|},\dfrac{c}{|\vec a|} )=(\dfrac{1}{\sqrt{14}}, \dfrac{2}{\sqrt{14}}, \dfrac{3}{\sqrt{14}})$

अतः, $\vec{a}$ के दिशा कोसाइन $(\dfrac{1}{\sqrt{14}}, \dfrac{2}{\sqrt{14}}, \dfrac{3}{\sqrt{14}})$ हैं।

13. बिंदुओं $A(1,2,-3)$ और $B(-1,-2,1)$ को जोड़ने वाले सदिश के दिशा कोसाइन ज्ञात कीजिए, जो $A$ से $B$ की ओर बिंदुओं के बीच बने हुए हैं।

उत्तर दिखाएं

हल

दिए गए बिंदु $A(1,2,-3)$ और $B(-1,-2,1)$ हैं।

$\therefore \overrightarrow{{}AB}=(-1-1) \hat{i}+(-2-2) \hat{j}+{1-(-3)} \hat{k}$

$\Rightarrow \overrightarrow{{}AB}=-2 \hat{i}-4 \hat{j}+4 \hat{k}$

$\therefore|\overrightarrow{{}AB}|=\sqrt{(-2)^{2}+(-4)^{2}+4^{2}}=\sqrt{4+16+16}=\sqrt{36}=6$

अतः, $\overrightarrow{{}AB}$ के दिशा कोसाइन $(-\dfrac{2}{6},-\dfrac{4}{6}, \dfrac{4}{6})=(-\dfrac{1}{3},-\dfrac{2}{3}, \dfrac{2}{3})$ हैं।

14. सिद्ध कीजिए कि सदिश $\hat{i}+\hat{j}+\hat{k}$ अक्ष OX, OY और OZ के समान झुके हुए है।

उत्तर दिखाएं

हल

मान लीजिए $\vec{a}=\hat{i}+\hat{j}+\hat{k}$।

तब,

$|\vec{a}|=\sqrt{1^{2}+1^{2}+1^{2}}=\sqrt{3}$

इसलिए, $\vec{a}$ के दिशा अनुपात $(\dfrac{1}{\sqrt{3}}, \dfrac{1}{\sqrt{3}}, \dfrac{1}{\sqrt{3}})$ हैं।

अब, मान लीजिए $a, \beta$, और $y$ वह कोण हैं जो $\vec{a}$ द्वारा $x, y$, और $z$ अक्षों के धनात्मक दिशा से बनते हैं।

तब, हमें $\cos \alpha=\dfrac{1}{\sqrt{3}}, \cos \beta=\dfrac{1}{\sqrt{3}}, \cos \gamma=\dfrac{1}{\sqrt{3}}$ मिलता है।

इसलिए, दिया गया सदिश OX, OY, और OZ अक्षों से समान ढलान पर झुका हुआ है।

15. दो बिंदुओं $P$ और $Q$ के स्थिति सदिश $\hat{i}+2 \hat{j}-\hat{k}$ और $-\hat{i}+\hat{j}+\hat{k}$ क्रमशः हैं, जो एक रेखा के बिंदु हैं। एक बिंदु $R$ का स्थिति सदिश ज्ञात कीजिए जो इन दो बिंदुओं को $2: 1$ के अनुपात में विभाजित करता है।

(i) आंतरिक रूप से

(ii) बाहरी रूप से

उत्तर दिखाएं

हल

दो बिंदुओं $P$ और $Q$ के बीच रेखा के बिंदु $R$ का स्थिति सदिश जो अनुपात $m: n$ में विभाजित करता है, निम्नलिखित द्वारा दिया जाता है:

i. आंतरिक रूप से: $\dfrac{m \vec{b}+n \vec{a}}{m+n}$

ii. बाहरी रूप से:

$\dfrac{m \vec{b}-n \vec{a}}{m-n}$

$P$ और $Q$ के स्थिति सदिश निम्नलिखित हैं:

$\overrightarrow{{}OP}=\hat{i}+2 \hat{j}-\hat{k}$ और $\overrightarrow{{}OQ}=-\hat{i}+\hat{j}+\hat{k}$

(i) दो बिंदुओं $P$ और $Q$ के बीच रेखा के बिंदु $R$ का स्थिति सदिश जो $2: 1$ के अनुपात में आंतरिक रूप से विभाजित करता है, निम्नलिखित द्वारा दिया जाता है,

$ \begin{aligned} \overrightarrow{{}OR} & =\dfrac{2(-\hat{i}+\hat{j}+\hat{k})+1(\hat{i}+2 \hat{j}-\hat{k})}{2+1}=\dfrac{(-2 \hat{i}+2 \hat{j}+2 \hat{k})+(\hat{i}+2 \hat{j}-\hat{k})}{3} \\ & =\dfrac{-\hat{i}+4 \hat{j}+\hat{k}}{3}=-\dfrac{1}{3} \hat{i}+\dfrac{4}{3} \hat{j}+\dfrac{1}{3} \hat{k} \end{aligned} $

(ii) दो बिंदुओं $P$ और $Q$ के बीच रेखा के बिंदु $R$ का स्थिति सदिश जो $2: 1$ के अनुपात में बाहरी रूप से विभाजित करता है, निम्नलिखित द्वारा दिया जाता है,

$ \begin{aligned} \overrightarrow{{}OR} & =\dfrac{2(-\hat{i}+\hat{j}+\hat{k})-1(\hat{i}+2 \hat{j}-\hat{k})}{2-1}=(-2 \hat{i}+2 \hat{j}+2 \hat{k})-(\hat{i}+2 \hat{j}-\hat{k}) \\

& =-3 \hat{i}+3 \hat{k} \end{aligned} $

16. $P(2,3,4)$ और $Q(4,1,-2)$ के बिंदुओं को मिलाने वाले वेक्टर के मध्य बिंदु का स्थिति सदिश ज्ञात कीजिए।

उत्तर दिखाएं

हल

$P(2,3,4)$ और $Q(4,1$, 2) के बिंदुओं को मिलाने वाले वेक्टर के मध्य बिंदु $R$ का स्थिति सदिश निम्नलिखित द्वारा दिया गया है,

$ \begin{aligned} \overrightarrow{{}OR} & =\dfrac{(2 \hat{i}+3 \hat{j}+4 \hat{k})+(4 \hat{i}+\hat{j}-2 \hat{k})}{2}=\dfrac{(2+4) \hat{i}+(3+1) \hat{j}+(4-2) \hat{k}}{2} \\ & =\dfrac{6 \hat{i}+4 \hat{j}+2 \hat{k}}{2}=3 \hat{i}+2 \hat{j}+\hat{k} \end{aligned} $

17. सिद्ध कीजिए कि स्थिति सदिश $\vec{a}=3 \hat{i}-4 \hat{j}-4 \hat{k}$, $\vec{b}=2 \hat{i}-\hat{j}+\hat{k}$ और $\vec{c}=\hat{i}-3 \hat{j}-5 \hat{k}$ के बिंदु $A, B$ और $C$ एक समकोण त्रिभुज के शीर्ष हैं।

उत्तर दिखाएं

हल

बिंदु $A, B$ और $C$ के स्थिति सदिश क्रमशः निम्नलिखित द्वारा दिए गए हैं:

$\vec{a}=3 \hat{i}-4 \hat{j}-4 \hat{k}, \vec{b}=2 \hat{i}-\hat{j}+\hat{k}$ और $\vec{c}=\hat{i}-3 \hat{j}-5 \hat{k}$

$\therefore \overrightarrow{{}AB}=\vec{b}-\vec{a}=(2-3) \hat{i}+(-1+4) \hat{j}+(1+4) \hat{k}=-\hat{i}+3 \hat{j}+5 \hat{k}$

$\overrightarrow{{}BC}=\vec{c}-\vec{b}=(1-2) \hat{i}+(-3+1) \hat{j}+(-5-1) \hat{k}=-\hat{i}-2 \hat{j}-6 \hat{k}$

$\overrightarrow{{}CA}=\vec{a}-\vec{c}=(3-1) \hat{i}+(-4+3) \hat{j}+(-4+5) \hat{k}=2 \hat{i}-\hat{j}+\hat{k}$

$\therefore|\overrightarrow{{}AB}|^{2}=(-1)^{2}+3^{2}+5^{2}=1+9+25=35$

$|\overrightarrow{{}BC}|^{2}=(-1)^{2}+(-2)^{2}+(-6)^{2}=1+4+36=41$

$|\overrightarrow{{}CA}|^{2}=2^{2}+(-1)^{2}+1^{2}=4+1+1=6$

$\therefore|\overrightarrow{{}AB}|^{2}+|\overrightarrow{{}CA}|^{2}=35+6=41=|\overrightarrow{{}BC}|^{2}$

अतः, $A B C$ एक समकोण त्रिभुज है।

18. त्रिभुज $ABC$ (चित्र 10.18) में निम्नलिखित में से कौन सा कथन सत्य नहीं है:

$\quad\quad$(A) $\overrightarrow{{}AB}+\overrightarrow{{}BC}+\overrightarrow{{}CA}=\overrightarrow{{}0}$

$\quad\quad$(B) $\overrightarrow{{}AB}+\overrightarrow{{}BC}-\overrightarrow{{}AC}=\overrightarrow{{}0}$

$\quad\quad$(सी) $\overrightarrow{{}AB}+\overrightarrow{{}BC}-\overrightarrow{{}CA}=\overrightarrow{{}0}$

$\quad\quad$(डी) $\overrightarrow{{}AB}-\overrightarrow{{}CB}+\overrightarrow{{}CA}=\overrightarrow{{}0}$

चित्र 10.18

उत्तर दिखाएं

}

हल

दिए गए त्रिभुज में योग के त्रिभुज नियम के अनुपालन करते हुए, हम निम्नलिखित प्राप्त करते हैं:

$$ \begin{align*} & \overrightarrow{{}AB}+\overrightarrow{{}BC}=\overrightarrow{{}AC} \tag{1}\\ & \Rightarrow \overrightarrow{{}AB}+\overrightarrow{{}BC}=-\overrightarrow{{}CA} \\ & \Rightarrow \overrightarrow{{}AB}+\overrightarrow{{}BC}+\overrightarrow{{}CA}=\overrightarrow{{}0} \tag{2} \end{align*} $$

$\therefore$ विकल्प $A$ में दी गई समीकरण सही है।

$\overrightarrow{{}AB}+\overrightarrow{{}BC}=\overrightarrow{{}AC}$

$\Rightarrow \overrightarrow{{}AB}+\overrightarrow{{}BC}-\overrightarrow{{}AC}=\overrightarrow{{}0}$

$\therefore$ विकल्प $B$ में दी गई समीकरण सही है।

समीकरण (2) से, हम निम्नलिखित प्राप्त करते हैं:

$\overrightarrow{{}AB}-\overrightarrow{{}CB}+\overrightarrow{{}CA}=\overrightarrow{{}0}$

$\therefore$ विकल्प $D$ में दी गई समीकरण सही है।

अब, विकल्प $C$ में दी गई समीकरण को ध्यान में रखते हैं:

$\overrightarrow{{}AB}+\overrightarrow{{}BC}-\overrightarrow{{}CA}=\overrightarrow{{}0}$

$\Rightarrow \overrightarrow{{}AB}+\overrightarrow{{}BC}=\overrightarrow{{}CA}$

समीकरण (1) और (3) से, हम निम्नलिखित प्राप्त करते हैं:

$ \overrightarrow{{}AC}=\overrightarrow{{}CA} $

$\Rightarrow \overrightarrow{{}AC}=-\overrightarrow{{}AC}$

$\Rightarrow \overrightarrow{{}AC}+\overrightarrow{{}AC}=\overrightarrow{{}0}$

$\Rightarrow 2 \overrightarrow{{}AC}=\overrightarrow{{}0}$

$\Rightarrow \overrightarrow{{}AC}=\overrightarrow{{}0}$, जो सही नहीं है।

इसलिए, विकल्प $C$ में दी गई समीकरण गलत है।

सही उत्तर $\mathbf{C}$ है।

19. यदि $\vec{a}$ और $\vec{b}$ दो समरेख वेक्टर हैं, तो निम्नलिखित में से कौन सा गलत है:

(A) $\vec{b}=\lambda \vec{a}$, किसी भी अदिश $\lambda$ के लिए

(B) $\vec{a}= \pm \vec{b}$

(C) $\vec{a}$ और $\vec{b}$ के संगत घटक समानुपाती नहीं हैं

(D) दोनों वेक्टर $\vec{a}$ और $\vec{b}$ एक ही दिशा में हैं, लेकिन अलग-अलग परिमाण रखते हैं।

उत्तर दिखाएं

हल

(A) $b=λa,$ किसी भी अदिश λ के लिए:

इस कथन को सही माना जा सकता है। यदि दो वेक्टर समरेख होते हैं, तो एक दूसरे का अदिश गुणज हो सकता है।

(B) $ \vec a=± \vec b:$

इस कथन को गलत माना जा सकता है। समरेख वेक्टर आवश्यक रूप से एक दूसरे के विपरीत दिशा में नहीं होते हैं; वे केवल एक दूसरे के अदिश गुणज हो सकते हैं।

(C) $\vec{a}$ और $\vec{b}$ के संगत घटक समानुपाती नहीं हैं:

इस कथन को गलत माना जा सकता है। दो वेक्टर समरेख होने के लिए, उनके संगत घटक समानुपाती होना आवश्यक है।

यदि $\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ और $\vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$, तो

$\vec{b}=\lambda \vec{a}$.

$\Rightarrow b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}=\lambda(a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k})$

$\Rightarrow b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}=(\lambda a_1) \hat{i}+(\lambda a_2) \hat{j}+(\lambda a_3) \hat{k}$

$\Rightarrow b_1=\lambda a_1, b_2=\lambda a_2, b_3=\lambda a_3$

$\Rightarrow \dfrac{b_1}{a_1}=\dfrac{b_2}{a_2}=\dfrac{b_3}{a_3}=\lambda$

इसलिए, $\vec{a}$ और $\vec{b}$ के संगत घटक समानुपाती होते हैं।

(D) दोनों वेक्टर $\vec a$ और $\vec b$ एक ही दिशा में हैं, लेकिन अलग-अलग परिमाण रखते हैं:

इस कथन को गलत माना जा सकता है। यही बात है कि समरेख वेक्टर एक ही दिशा में हो सकते हैं, लेकिन आवश्यक रूप से ऐसा नहीं होना आवश्यक है। यदि एक वेक्टर दूसरे का ऋणात्मक अदिश गुणज होता है, तो वे विपरीत दिशा में हो सकते हैं।

इसलिए, कथन $(B)$,$(C)$ और $(D)$ गलत हैं।

10.6 दो सदिशों का गुणनफल

अब तक हम दो सदिशों के योग और व्यवकलन के बारे में अध्ययन कर चुके हैं। दो सदिशों के गुणन के बारे में भी चर्चा करने की योजना बनाई गई है। हम याद कर सकते हैं कि दो संख्याओं का गुणनफल एक संख्या होता है, दो आव्यूहों का गुणनफल फिर एक आव्यूह होता है। लेकिन फलनों के मामले में, हम दो फलनों को दो तरीकों से गुणा कर सकते हैं, अर्थात दो फलनों के बिंदुवार गुणन और दो फलनों के संयोजन। इसी तरह, दो सदिशों के गुणन को भी दो तरीकों से परिभाषित किया गया है, अर्थात सदिश (या डॉट) गुणन जहां परिणाम एक सदिश होता है, और सदिश (या क्रॉस) गुणन जहां परिणाम एक सदिश होता है। इन दो प्रकार के गुणन के आधार पर, सदिशों के विभिन्न अनुप्रयोग ज्यामिति, भौतिकी और इंजीनियरिंग में पाए जाते हैं। इस अनुच्छेद में, हम इन दो प्रकार के गुणन के बारे में चर्चा करेंगे।

10.6.1 दो सदिशों का सदिश (या डॉट) गुणन

परिभाषा 2 दो गैर-शून्य सदिश $\vec{a}$ और $\vec{b}$ के सदिश गुणन को $\vec{a} \cdot \vec{b}$ से नोट किया जाता है, जो परिभाषित किया गया है:

$$ \qquad \qquad \qquad \vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta $$

जहां, $\theta$ दो सदिश $\vec{a}$ और $\vec{b}$ के बीच का कोण है, $0 \leq \theta \leq \pi$ (चित्र 10.19)।

यदि $\vec{a}=0$ या $\vec{b}=0$ हो तो $\theta$ परिभाषित नहीं होता है, और इस मामले में हम $\vec{a} \cdot \vec{b}=0$ के रूप में परिभाषित करते हैं।

चित्र 10.19

अवलोकन

1. $\vec{a} \cdot \vec{b}$ एक वास्तविक संख्या है।

2. मान लीजिए $\vec{a}$ और $\vec{b}$ दो गैर-शून्य सदिश हैं, तो $\vec{a} \cdot \vec{b}=0$ अगर और केवल अगर $\vec{a}$ और $\vec{b}$ एक दूसरे के लंब हों। अर्थात

$$ \qquad \qquad \qquad \vec{a} \cdot \vec{b}=0 \leftrightarrow \vec{a} \perp \vec{b} $$

3. यदि $\theta=0$, तो $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|$

विशेष रूप से, $\vec{a} \cdot \vec{a}=|\vec{a}|^{2}$, क्योंकि इस मामले में $\theta$ 0 है।

4. यदि $\theta=\pi$, तो $\vec{a} \cdot \vec{b}=-|\vec{a}||\vec{b}|$

विशेष रूप से, $\vec{a} \cdot \vec{b}=-|\vec{a}||\vec{b}|$, क्योंकि इस मामले में $\theta$ $\pi$ है।

5. दृष्टि आवश्यकताओं 2 और 3 के आधार पर, परस्पर लंब एकक वेक्टर $\hat{i}, \hat{j}$ और $\hat{k}$ के लिए हम निम्नलिखित प्राप्त करते हैं:

$ \qquad \qquad \qquad \begin{aligned} & \hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1, \\ & \hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=0 \end{aligned} $

6. दो गैर-शून्य वेक्टर $\vec{a}$ और $\vec{b}$ के बीच कोण निम्नलिखित द्वारा दिया जाता है:

$ \cos \theta=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}, \text{ या } \theta=\cos ^{-1}\left(\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\right) $

7. अदिश गुणन आविष्कारी होता है। अर्थात:

$ \qquad \qquad \qquad \vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a} $

अदिश गुणन के दो महत्वपूर्ण गुण

गुण 1 (अदिश गुणन की योग पर वितरण गुण) मान लीजिए कि $\vec{a}, \vec{b}$ और $\vec{c}$ कोई तीन वेक्टर हैं, तो:

$ \qquad \qquad \qquad \vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c} $

गुण 2 मान लीजिए कि $\vec{a}$ और $\vec{b}$ कोई दो वेक्टर हैं, और 1 कोई अदिश है। तब:

$ \qquad \qquad \qquad (\lambda \vec{a}) \cdot \vec{b}=(\lambda \vec{a}) \cdot \vec{b}=\lambda(\vec{a} \cdot \vec{b})=\vec{a} \cdot(\lambda \vec{b}) $

यदि दो वेक्टर $\vec{a}$ और $\vec{b}$ घटक रूप में $a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ और $b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$ के रूप में दिए गए हों, तो उनका अदिश गुणन निम्नलिखित द्वारा दिया जाता है:

$ \qquad \qquad \qquad \begin{aligned} \vec{a} \cdot \vec{b}= & (a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}) \cdot(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}) \\ = & a_1 \hat{i} \cdot(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k})+a_2 \hat{j} \cdot(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k})+a_3 \hat{k} \cdot(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}) \\ = & a_1 b_1(\hat{i} \cdot \hat{i})+a_1 b_2(\hat{i} \cdot \hat{j})+a_1 b_3(\hat{i} \cdot \hat{k})+a_2 b_1(\hat{j} \cdot \hat{i})+a_2 b_2(\hat{j} \cdot \hat{j})+a_2 b_3(\hat{j} \cdot \hat{k})\\ & +a_3 b_1(\hat{k} \cdot \hat{i})+a_3 b_2(\hat{k} \cdot \hat{j})+a_3 b_3(\hat{k} \cdot \hat{k}) \text{ (उपरोक्त गुण 1 और 2 का उपयोग करके) } \\

= & a_1 b_1+a_2 b_2+a_3 b_3 \qquad \text{ (अवलोकन 5 का उपयोग करके) } \\ \end{aligned} $

इसलिए $\qquad \qquad \vec{a} \cdot \vec{b}=a_1 b_1+a_2 b_2+a_3 b_3$

10.6.2 एक सदिश के एक रेखा पर प्रक्षेपण

मान लीजिए एक सदिश $\overrightarrow{{}AB}$ एक दिए गए दिशा रेखा $l$ (मान लीजिए) के साथ कोण $\theta$ बनाती है (अंतर्दिशीय दिशा में, चित्र 10.20 में)। तब $\overrightarrow{{}AB}$ के रेखा $l$ पर प्रक्षेपण एक सदिश $\vec{p}$ (मान लीजिए) होता है, जिसका परिमाण $|\overrightarrow{{}AB}||\cos \theta|$ होता है, और $\vec{p}$ की दिशा रेखा $l$ की दिशा के समान (या विपरीत) होती है, जिसके आधार पर $\cos \theta$ धनात्मक या ऋणात्मक होता है।

चित्र 10.20

सदिश $\vec{p}$ को प्रक्षेपण सदिश कहते हैं, और इसका परिमाण $|\vec{p}|$ वही प्रक्षेपण होता है जो सदिश $\overrightarrow{{}AB}$ के दिशा रेखा $l$ पर होता है।

उदाहरण के लिए, निम्नलिखित चित्रों (चित्र 10.20 (i) से (iv)) में से प्रत्येक में $\overrightarrow{{}AB}$ के रेखा $l$ के अनुदिश प्रक्षेपण सदिश $\overrightarrow{{}AC}$ होता है।

अवलोकन

1. यदि $\hat{p}$ एक रेखा $l$ के अनुदिश एक एकक सदिश हो, तो एक सदिश $\vec{a}$ के रेखा $l$ पर प्रक्षेपण को $\vec{a} \cdot \hat{p}$ द्वारा दिया जाता है।

2. एक सदिश $\vec{a}$ के दूसरे सदिश $\vec{b}$ पर प्रक्षेपण को निम्नलिखित द्वारा दिया जाता है

$ \qquad \qquad \qquad \vec{a} \cdot \hat{b}, \quad \text{ या } \quad \vec{a} \cdot\left(\dfrac{\vec{b}}{|\vec{b}|}\right), \text{ या } \dfrac{1}{|\vec{b}|}(\vec{a} \cdot \vec{b}) $

3. यदि $\theta=0$, तो $\overrightarrow{{}A B}$ का प्रक्षेपण सदिश $\overrightarrow{{}A B}$ ही होता है और यदि $\theta=\pi$, तो $\overrightarrow{{}AB}$ का प्रक्षेपण सदिश $\overrightarrow{{}BA}$ होता है।

4. यदि $\theta=\dfrac{\pi}{2}$ या $\theta=\dfrac{3 \pi}{2}$, तो $\overrightarrow{{}A B}$ का प्रक्षेपण सदिश शून्य सदिश होता है।

टिप्पणी यदि $\alpha, \beta$ और $\gamma$ सदिश $\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ के दिशा कोण हों, तो इसके दिशा अनुपात निम्नलिखित द्वारा दिया जा सकता है

$ \qquad \qquad \qquad \cos \alpha=\dfrac{\vec{a} \cdot \hat{i}}{|\vec{a}||\hat{i}|}=\dfrac{a_1}{|\vec{a}|}, \cos \beta=\dfrac{a_2}{|\vec{a}|}, \text{ और } \cos \gamma=\dfrac{a_3}{|\vec{a}|} $

इसके अलावा, ध्यान दें कि $|\vec{a}| \cos \alpha,|\vec{a}| \cos \beta$ और $|\vec{a}| \cos \gamma$ क्रमशः $\vec{a}$ के $OX, OY$ और $OZ$ के अनुदिश प्रक्षेप हैं। अर्थात, सदिश $\vec{a}$ के अदिश घटक $a_1, a_2$ और $a_3$ क्रमशः $\vec{a}$ के $x$-अक्ष, $y$-अक्ष और $z$-अक्ष के अनुदिश प्रक्षेप हैं। इसके अतिरिक्त, यदि $\vec{a}$ एक एकक सदिश है, तो इसे इसके दिशा कोज्या के रूप में व्यक्त किया जा सकता है:

$ \qquad \qquad \qquad \vec{a}=\cos \alpha \hat{i}+\cos \beta \hat{j}+\cos \gamma \hat{k} $

उदाहरण 13 दो सदिश $\vec{a}$ और $\vec{b}$ के बीच कोण ज्ञात कीजिए जिनके परिमाण क्रमशः 1 और 2 हैं और जब $\vec{a} \cdot \vec{b}=1$ हो।

हल दिया गया है $\vec{a} \cdot \vec{b}=1,|\vec{a}|=1$ और $|\vec{b}|=2$। हम लिख सकते हैं:

$ \qquad \qquad \qquad \theta=\cos ^{-1}\left(\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\right)=\cos ^{-1}\left(\dfrac{1}{2}\right)=\dfrac{\pi}{3} $

उदाहरण 14 दो सदिश $\vec{a}=\hat{i}+\hat{j}-\hat{k}$ और $\vec{b}=\hat{i}-\hat{j}+\hat{k}$ के बीच कोण ’ $\theta$ ’ ज्ञात कीजिए।

हल दो सदिश $\vec{a}$ और $\vec{b}$ के बीच कोण $\theta$ निम्नलिखित द्वारा दिया गया है:

$ \qquad \qquad \qquad \cos \theta=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} $

अब $\qquad \qquad \vec{a} \cdot \vec{b}=(\hat{i}+\hat{j}-\hat{k}) \cdot(\hat{i}-\hat{j}+\hat{k})=1-1-1=-1$

इसलिए, हम लिख सकते हैं $\quad \cos \theta=\dfrac{-1}{3}$

अतः अभीष्ट कोण है $ \qquad \theta=\cos ^{-1}\left(-\dfrac{1}{3}\right) $

उदाहरण 15 यदि $\vec{a}=5 \hat{i}-\hat{j}-3 \hat{k}$ और $\vec{b}=\hat{i}+3 \hat{j}-5 \hat{k}$, तो दिखाइए कि सदिश $\vec{a}+\vec{b}$ और $\vec{a}-\vec{b}$ लंबवत हैं।

हल हम जानते हैं कि दो गैर-शून्य सदिश लंबवत होते हैं यदि उनका अदिश गुणनफल शून्य होता है।

यहाँ $ \qquad \qquad \vec{a}+\vec{b}=(5 \hat{i}-\hat{j}-3 \hat{k})+(\hat{i}+3 \hat{j}-5 \hat{k})=6 \hat{i}+2 \hat{j}-8 \hat{k}

$

और $ \qquad \qquad \vec{a}-\vec{b}=(5 \hat{i}-\hat{j}-3 \hat{k})-(\hat{i}+3 \hat{j}-5 \hat{k})=4 \hat{i}-4 \hat{j}+2 \hat{k} $

इसलिए $ \qquad \qquad (\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})=(6 \hat{i}+2 \hat{j}-8 \hat{k}) \cdot(4 \hat{i}-4 \hat{j}+2 \hat{k})=24-8-16=0 $

इसलिए $\qquad \qquad \vec{a}+\vec{b}$ और $\vec{a}-\vec{b}$ लम्ब भुजा हैं।

उदाहरण 16 सदिश $\vec{a}=2 \hat{i}+3 \hat{j}+2 \hat{k}$ के सदिश $\vec{b}=\hat{i}+2 \hat{j}+\hat{k}$ पर प्रक्षेप ज्ञात कीजिए।

हल सदिश $\vec{a}$ के सदिश $\vec{b}$ पर प्रक्षेप इस प्रकार दिया गया है

$ \qquad \qquad \qquad\dfrac{1}{|\vec{b}|}(\vec{a} \cdot \vec{b})=\dfrac{(2 \times 1+3 \times 2+2 \times 1)}{\sqrt{(1)^{2}+(2)^{2}+(1)^{2}}}=\dfrac{10}{\sqrt{6}}=\dfrac{5}{3} \sqrt{6} $

उदाहरण 17 यदि दो सदिश $\vec{a}$ और $\vec{b}$ इस प्रकार हैं कि $|\vec{a}|=2,|\vec{b}|=3$ और $\vec{a} \cdot \vec{b}=4$, तो $|\vec{a}-\vec{b}|$ ज्ञात कीजिए।

हल हम जानते हैं

$ \qquad \qquad \qquad\begin{aligned} |\vec{a}-\vec{b}|^{2} & =(\vec{a}-\vec{b}) \cdot(\vec{a}-\vec{b}) \\ & =\vec{a} \cdot \vec{a}-\vec{a} \cdot \vec{b}-\vec{b} \cdot \vec{a}+\vec{b} \cdot \vec{b} \end{aligned} $

$ \qquad \qquad \qquad \qquad \quad\begin{aligned} & =|\vec{a}|^{2}-2(\vec{a} \cdot \vec{b})+|\vec{b}|^{2} \\ & =(2)^{2}-2(4)+(3)^{2} \end{aligned} $

इसलिए $\qquad \quad |\vec{a}|-\vec{b}=\sqrt{5}$

उदाहरण 18 यदि $\vec{a}$ एक एकक सदिश है और $(\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=8$, तो $|\vec{x}|$ ज्ञात कीजिए।

हल क्योंकि $\vec{a}$ एक एकक सदिश है, इसलिए $|\vec{a}|=1$। अतः,

$ \qquad \qquad \qquad(\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=8 $

या $ \qquad \qquad \qquad\vec{x} \cdot \vec{x}+\vec{x} \cdot \vec{a}-\vec{a} \cdot \vec{x}-\vec{a} \cdot \vec{a}=8 $

या $ \qquad \qquad \qquad|\vec{x}|^{2}-1=8 \text{ अर्थात }|\vec{x}|^{2}=9 $

इसलिए $\qquad \quad |\vec{x}|=3 $ (किसी सदिश के परिमाण धनात्मक नहीं हो सकते)।

उदाहरण 19 किसी भी दो सदिश $\vec{a}$ और $\vec{b}$ के लिए हमें हमेसा $|\vec{a} \cdot \vec{b}| \leq|\vec{a}||\vec{b}|$ (कौशी-श्वार्ज असमानुपाति) होता है।

हल असमिका तब बर्बत रहती है जब या तो $\vec{a}=\overrightarrow{{}0}$ या $\vec{b}=\overrightarrow{{}0}$ हो। वास्तव में, ऐसी स्थिति में हमें $|\vec{a} \cdot \vec{b}|=0=|\vec{a}||\vec{b}|$ प्राप्त होता है। इसलिए, हम मान लें कि $|\vec{a}| \neq 0 \neq|\vec{b}|$।

तब हमें निम्नलिखित प्राप्त होता है

$ \qquad \qquad \qquad \qquad \dfrac{|\vec{a} \cdot \vec{b}|}{|\vec{a} | \vec{b}|}=|\cos \theta| \leq 1 $

इसलिए $\qquad \qquad |\vec{a} \cdot \vec{b}| \leq|\vec{a}||\vec{b}|$

चित्र 10.21

उदाहरण 20 किसी भी दो सदिश $\vec{a}$ और $\vec{b}$ के लिए हमें हमेसा $|\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|$ (त्रिभुज असमिका) प्राप्त होता है।

हल असमिका तब बर्बत रहती है जब या तो $\vec{a}=\overrightarrow{0} \text { या } \vec{b}=\overrightarrow{0}$ (कैसे?)। इसलिए, मान लें कि $|\vec{a}| \neq \overrightarrow{0} \neq|\vec{b}|$। तब,

$ \qquad \qquad \qquad\begin{aligned} |\vec{a}+\vec{b}|^{2}= & (\vec{a}+\vec{b})^{2}=(\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b}) \\ = & \vec{a} \cdot \vec{a}+\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{a}+\vec{b} \cdot \vec{b} \\ = & |\vec{a}|^{2}+2 \vec{a} \cdot \vec{b}+|\vec{b}|^{2} \\ \leq & |\vec{a}|^{2}+2|\vec{a} \cdot \vec{b}|+|\vec{b}|^{2} \\ \leq & |\vec{a}|^{2}+2|\vec{a}||\vec{b}|+|\vec{b}|^{2} \\ = & (|\vec{a}|+|\vec{b}|)^{2} \end{aligned} $

इसलिए $\qquad \qquad \qquad |\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|$

टिप्पणी यदि त्रिभुज असमिका में समानता लागू होती है (ऊपर के उदाहरण 20 में), अर्थात

$ \qquad \qquad \qquad|\vec{a}+\vec{b}| =|\vec{a}|+|\vec{b}| $

तो $\qquad \qquad \quad|\overrightarrow{{}AC}| =|\overrightarrow{{}AB}|+|\overrightarrow{{}BC}|$

इसका अर्थ है कि बिंदु $A, B$ और $C$ संरेख होते हैं।

उदाहरण 21 सिद्ध करें कि बिंदु $A(-2 \hat{i}+3 \hat{j}+5 \hat{k}), B(\hat{i}+2 \hat{j}+3 \hat{k})$ और $C(7 \hat{i}-\hat{k})$ संरेख होते हैं।

हल हमें निम्नलिखित प्राप्त होता है

$ \qquad \qquad \qquad \begin{aligned} \overrightarrow{{}AB} & =(1+2) \hat{i}+(2-3) \hat{j}+(3-5) \hat{k}=3 \hat{i}-\hat{j}-2 \hat{k} \\ \overrightarrow{{}BC} & =(7-1) \hat{i}+(0-2) \hat{j}+(-1-3) \hat{k}=6 \hat{i}-2 \hat{j}-4 \hat{k} \\ \overrightarrow{{}AC} & =(7+2) \hat{i}+(0-3) \hat{j}+(-1-5) \hat{k}=9 \hat{i}-3 \hat{j}-6 \hat{k} \\ |\overrightarrow{{}AB}| & =\sqrt{14},|\overrightarrow{{}BC}|=2 \sqrt{14} \text{ and }|\overrightarrow{{}AC}|=3 \sqrt{14} \end{aligned} $

इसलिए $ \qquad \quad|\overrightarrow{{}AC}|=|\overrightarrow{{}AB}|+|\overrightarrow{{}BC}| $

इसलिए बिंदु A, B और C संरेख हैं।

नोट उदाहरण 21 में, एक ध्यान दें कि भले ही $\overrightarrow{{}AB}+\overrightarrow{{}BC}+\overrightarrow{{}CA}=\overrightarrow{{}0}$ है, लेकिन बिंदु $A, B$ और $C$ एक त्रिभुज के शीर्ष नहीं बनाते।

अभ्यास 10.3

1. सदिश $\vec{a}$ और $\vec{b}$ के बीच कोण ज्ञात कीजिए, जिनके परिमाण क्रमशः $\sqrt{3}$ और 2 हैं तथा $\vec{a} \cdot \vec{b}=\sqrt{6}$ है।

उत्तर दिखाएं

हल

दिया गया है,

$|\vec{a}|=\sqrt{3},|\vec{b}|=2$ और, $\vec{a} \cdot \vec{b}=\sqrt{6}$

अब, हम जानते हैं कि $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta$।

$\therefore \sqrt{6}=\sqrt{3} \times 2 \times \cos \theta$

$\Rightarrow \cos \theta=\frac{\sqrt{6}}{\sqrt{3} \times 2}$

$\Rightarrow \cos \theta=\frac{1}{\sqrt{2}}$

$\Rightarrow \theta=\frac{\pi}{4}$

अतः, दिए गए सदिश $\vec{a}$ और $\vec{b}$ के बीच कोण $\frac{\pi}{4}$ है।

2. सदिश $\hat{i}-2 \hat{j}+3 \hat{k}$ और $3 \hat{i}-2 \hat{j}+\hat{k}$ के बीच कोण ज्ञात कीजिए।

उत्तर दिखाएं

हल

दिए गए सदिश $\vec{a}=\hat{i}-2 \hat{j}+3 \hat{k}$ और $\vec{b}=3 \hat{i}-2 \hat{j}+\hat{k}$ हैं।

$ \begin{aligned} & |\vec{a}|=\sqrt{1^{2}+(-2)^{2}+3^{2}}=\sqrt{1+4+9}=\sqrt{14} \\ & |\vec{b}|=\sqrt{3^{2}+(-2)^{2}+1^{2}}=\sqrt{9+4+1}=\sqrt{14} \end{aligned} $

अब, $\vec{a} \cdot \vec{b}=(\hat{i}-2 \hat{j}+3 \hat{k})(3 \hat{i}-2 \hat{j}+\hat{k})$

$ \begin{aligned} & =1.3+(-2)(-2)+3.1 \\ & =3+4+3 \\ & =10 \end{aligned} $

इसके अतिरिक्त, हम जानते हैं कि $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta$

$\therefore 10=\sqrt{14} \sqrt{14} \cos \theta$

$\Rightarrow \cos \theta=\frac{10}{14}$

$\Rightarrow \theta=\cos ^{-1}(\frac{5}{7})$

3. सदिश $\hat{i}-\hat{j}$ के सदिश $\hat{i}+\hat{j}$ पर प्रक्षेप ज्ञात कीजिए।

उत्तर दिखाएं

हल

मान लीजिए $\vec{a}=\hat{i}-\hat{j}$ और $\vec{b}=\hat{i}+\hat{j}$ हैं।

अब, सदिश $\vec{a}$ के सदिश $\vec{b}$ पर प्रक्षेप निम्नलिखित द्वारा दिया गया है,

$\frac{1}{|\vec{b}|}(\vec{a} \cdot \vec{b})=\frac{1}{\sqrt{1+1}}(1.1+(-1)(1))=\frac{1}{\sqrt{2}}(1-1)=0$

अतः, सदिश $\vec{a}$ के सदिश $\vec{b}$ पर प्रक्षेप 0 है।

4. सदिश $\hat{i}+3 \hat{j}+7 \hat{k}$ के सदिश $7 \hat{i}-\hat{j}+8 \hat{k}$ पर प्रक्शन ज्ञात कीजिए।

उत्तर दिखाएं

हल

मान लीजिए $\vec{a}=\hat{i}+3 \hat{j}+7 \hat{k}$ और $\vec{b}=7 \hat{i}-\hat{j}+8 \hat{k}$।

अब, सदिश $\vec{a}$ के सदिश $\vec{b}$ पर प्रक्शन निम्नलिखित द्वारा दिया जाता है,

$\frac{1}{|\vec{b}|}(\vec{a} \cdot \vec{b})=\frac{1}{\sqrt{7^{2}+(-1)^{2}+8^{2}}}(1(7)+3(-1)+7(8))=\frac{7-3+56}{\sqrt{49+1+64}}=\frac{60}{\sqrt{114}}$

5. दिए गए तीन सदिशों में से प्रत्येक के एक इकाई सदिश होने को सिद्ध कीजिए:

$$ \frac{1}{7}(2 \hat{i}+3 \hat{j}+6 \hat{k}), \frac{1}{7}(3 \hat{i}-6 \hat{j}+2 \hat{k}), \quad \frac{1}{7}(6 \hat{i}+2 \hat{j}-3 \hat{k}) $$

इसके अलावा, दिखाइए कि वे एक-दूसरे से लंब हैं।

उत्तर दिखाएं

हल

मान लीजिए $\vec{a}=\frac{1}{7}(2 \hat{i}+3 \hat{j}+6 \hat{k})=\frac{2}{7} \hat{i}+\frac{3}{7} \hat{j}+\frac{6}{7} \hat{k}$,

$\vec{b}=\frac{1}{7}(3 \hat{i}-6 \hat{j}+2 \hat{k})=\frac{3}{7} \hat{i}-\frac{6}{7} \hat{j}+\frac{2}{7} \hat{k}$,

$\vec{c}=\frac{1}{7}(6 \hat{i}+2 \hat{j}-3 \hat{k})=\frac{6}{7} \hat{i}+\frac{2}{7} \hat{j}-\frac{3}{7} \hat{k}$।

$|\vec{a}|=\sqrt{(\frac{2}{7})^{2}+(\frac{3}{7})^{2}+(\frac{6}{7})^{2}}=\sqrt{\frac{4}{49}+\frac{9}{49}+\frac{36}{49}}=1$

$|\vec{b}|=\sqrt{(\frac{3}{7})^{2}+(-\frac{6}{7})^{2}+(\frac{2}{7})^{2}}=\sqrt{\frac{9}{49}+\frac{36}{49}+\frac{4}{49}}=1$

$|\vec{c}|=\sqrt{(\frac{6}{7})^{2}+(\frac{2}{7})^{2}+(-\frac{3}{7})^{2}}=\sqrt{\frac{36}{49}+\frac{4}{49}+\frac{9}{49}}=1$

इस प्रकार, दिए गए तीन सदिशों में से प्रत्येक एक इकाई सदिश है।

$\vec{a} \cdot \vec{b}=\frac{2}{7} \times \frac{3}{7}+\frac{3}{7} \times(\frac{-6}{7})+\frac{6}{7} \times \frac{2}{7}=\frac{6}{49}-\frac{18}{49}+\frac{12}{49}=0$

$\vec{b} \cdot \vec{c}=\frac{3}{7} \times \frac{6}{7}+(\frac{-6}{7}) \times \frac{2}{7}+\frac{2}{7} \times(\frac{-3}{7})=\frac{18}{49}-\frac{12}{49}-\frac{6}{49}=0$

$\vec{c} \cdot \vec{a}=\frac{6}{7} \times \frac{2}{7}+\frac{2}{7} \times \frac{3}{7}+(\frac{-3}{7}) \times \frac{6}{7}=\frac{12}{49}+\frac{6}{49}-\frac{18}{49}=0$

इसलिए, दिए गए तीन वेक्टर एक दूसरे के साथ परस्पर लम्ब हैं।

6. यदि $(\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})=8$ और $|\vec{a}|=8|\vec{b}|$, तो $|\vec{a}|$ और $|\vec{b}|$ ज्ञात कीजिए।

उत्तर दिखाएं

हल

$(\vec{a} \cdot \vec{b}) \cdot(\vec{a}-\vec{b})=8$

$\Rightarrow \vec{a} \cdot \vec{a}-\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{a}-\vec{b} \cdot \vec{b}=8$

$\Rightarrow|\vec{a}|^{2}-|\vec{b}|^{2}=8$

$\Rightarrow(8|\vec{b}|)^{2}-|\vec{b}|^{2}=8 \quad[|\vec{a}|=8|\vec{b}|]$

$\Rightarrow 64|\vec{b}|^{2}-|\vec{b}|^{2}=8$

$\Rightarrow 63|\vec{b}|^{2}=8$

$\Rightarrow|\vec{b}|^{2}=\frac{8}{63}$

$\Rightarrow|\vec{b}|=\sqrt{\frac{8}{63}} \quad$ [वेक्टर के परिमाण धनात्मक नहीं हो सकते]

$\Rightarrow|\vec{b}|=\frac{2 \sqrt{2}}{3 \sqrt{7}}$

$|\vec{a}|=8|\vec{b}|=\frac{8 \times 2 \sqrt{2}}{3 \sqrt{7}}=\frac{16 \sqrt{2}}{3 \sqrt{7}}$

7. उत्पाद $(3 \vec{a}-5 \vec{b}) \cdot(2 \vec{a}+7 \vec{b})$ का मूल्यांकन कीजिए।

उत्तर दिखाएं

हल

$ \begin{aligned} & (3 \vec{a}-5 \vec{b}) \cdot(2 \vec{a}+7 \vec{b}) \\ & =3 \vec{a} \cdot 2 \vec{a}+3 \vec{a} \cdot 7 \vec{b}-5 \vec{b} \cdot 2 \vec{a}-5 \vec{b} \cdot 7 \vec{b}, \quad (\because \vec a \cdot \vec b= \vec b \cdot \vec a) \\ & =6 \vec{a} \cdot \vec{a}+21 \vec{a} \cdot \vec{b}-10 \vec{a} \cdot \vec{b}-35 \vec{b} \cdot \vec{b} \\ & =6|\vec{a}|^{2}+11 \vec{a} \cdot \vec{b}-35|\vec{b}|^{2} \end{aligned} $

8. दो वेक्टर $\vec{a}$ और $\vec{b}$ के परिमाण बराबर हैं और उनके बीच का कोण $60^{\circ}$ है तथा उनका अदिश गुणनफल $\frac{1}{2}$ है। दोनों वेक्टरों के परिमाण ज्ञात कीजिए।

उत्तर दिखाएं

हल

मान लीजिए $\theta$ वेक्टर $\vec{a}$ और $\vec{b}$ के बीच का कोण है।

दिया गया है कि $|\vec{a}|=|\vec{b}|, \vec{a} \cdot \vec{b}=\frac{1}{2}$, और $\theta=60^{\circ}$।

हम जानते हैं कि $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta$

$\therefore \frac{1}{2}=|\vec{a}||\vec{a}| \cos 60^{\circ}$

[उपयोग (1)]

$\Rightarrow \frac{1}{2}=|\vec{a}|^{2} \times \frac{1}{2}$

$\Rightarrow|\vec{a}|^{2}=1$

$\Rightarrow|\vec{a}|=|\vec{b}|=1$

9. यदि एक इकाई सदिश $\vec{a}$ के लिए, $(\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=12$ हो, तो $|\vec{x}|$ ज्ञात कीजिए।

उत्तर दिखाएं

हल

$(\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=12$

$\Rightarrow \vec{x} \cdot \vec{x}+\vec{x} \cdot \vec{a}-\vec{a} \cdot \vec{x}-\bar{{}a} \cdot \vec{a}=12, \quad (\because \vec a \cdot \vec b= \vec b \cdot \vec a)$

$\Rightarrow|\vec{x}|^{2}-|\vec{a}|^{2}=12$

$\Rightarrow|\vec{x}|^{2}-1=12 \quad[|\vec{a}|=1$ क्योंकि $\vec{a}$ एक इकाई सदिश है $]$

$\Rightarrow|\vec{x}|^{2}=13$

$\therefore|\vec{x}|=\sqrt{13}$

10. यदि $\vec{a}=2 \hat{i}+2 \hat{j}+3 \hat{k}, \vec{b}=-\hat{i}+2 \hat{j}+\hat{k}$ और $\vec{c}=3 \hat{i}+\hat{j}$ ऐसे हो कि $\vec{a}+\lambda \vec{b}$, $\vec{c}$ के लंबवत हो, तो $\lambda$ का मान ज्ञात कीजिए।

उत्तर दिखाएं

हल

दिए गए सदिश $\vec{a}=2 \hat{i}+2 \hat{j}+3 \hat{k}, \vec{b}=-\hat{i}+2 \hat{j}+\hat{k}$, और $\vec{c}=3 \hat{i}+\hat{j}$ हैं।

अब,

$\vec{a}+\lambda \vec{b}=(2 \hat{i}+2 \hat{j}+3 \hat{k})+\lambda(-\hat{i}+2 \hat{j}+\hat{k})=(2-\lambda) \hat{i}+(2+2 \lambda) \hat{j}+(3+\lambda) \hat{k}$

यदि $(\vec{a}+\lambda \vec{b})$ $\vec{c}$ के लंबवत हो, तो

$(\vec{a}+\lambda \vec{b}) \cdot \vec{c}=0$.

$\Rightarrow[(2-\lambda) \hat{i}+(2+2 \lambda) \hat{j}+(3+\lambda) \hat{k}] \cdot(3 \hat{i}+\hat{j})=0$

$\Rightarrow(2-\lambda) 3+(2+2 \lambda) 1+(3+\lambda) 0=0$

$\Rightarrow 6-3 \lambda+2+2 \lambda=0$

$\Rightarrow-\lambda+8=0$

$\Rightarrow \lambda=8$

अतः, $\lambda$ का अभीष्ट मान 8 है।

11. सिद्ध कीजिए कि $|\vec{a}| \vec{b}+|\vec{b}| \vec{a}$, कोई भी दो गैर-शून्य सदिश $\vec{a}$ और $\vec{b}$ के लिए $|\vec{a}| \vec{b}-|\vec{b}| \vec{a}$ के लंबवत होता है।

उत्तर दिखाएं

हल

$(|\vec{a}| \vec{b}+|\vec{b}| \vec{a}) \cdot(|\vec{a}| \vec{b}-|\vec{b}| \vec{a})$

$=|\vec{a}|^{2} \vec{b} \cdot \vec{b}-|\vec{a}||\vec{b}| \vec{b} \cdot \vec{a}+|\vec{b}||\vec{a}| \vec{a} \cdot \vec{b}-|\vec{b}|^{2} \vec{a} \cdot \vec{a}, \quad (\because \vec a \cdot \vec b= \vec b \cdot \vec a)$

$=|\vec{a}|^{2}|\vec{b}|^{2}-|\vec{b}|^{2}|\vec{a}|^{2}$

$=0$

इसलिए, $|\vec{a}| \vec{b}+|\vec{b}| \vec{a}$ और $|\vec{a}| \vec{b}-|\vec{b}| \vec{a}$ एक दूसरे के लंब हैं।

12. यदि $\vec{a} \cdot \vec{a}=0$ और $\vec{a} \cdot \vec{b}=0$, तो सदिश $\vec{b}$ के बारे में क्या निष्कर्ष निकाला जा सकता है ?

उत्तर दिखाएं

हल

दिया गया है कि $\vec{a} \cdot \vec{a}=0$ और $\vec{a} \cdot \vec{b}=0$।

अब,

$\vec{a} \cdot \vec{a}=0 \Rightarrow|\vec{a}|^{2}=0 \Rightarrow|\vec{a}|=0$

$\therefore \vec{a}$ एक शून्य सदिश है।

इसलिए, $\vec{a} \cdot \vec{b}=0$ को संतुष्ट करने वाला सदिश $\vec{b}$ कोई भी सदिश हो सकता है।

13. यदि $\vec{a}, \vec{b}, \vec{c}$ इकाई सदिश हैं जैसे कि $\vec{a}+\vec{b}+\vec{c}=\overrightarrow{{}0}$, तो $\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}$ का मान ज्ञात कीजिए।

उत्तर दिखाएं

हल

हमें दिया गया है $|\overrightarrow{\mathrm{a}}|=1,|\overrightarrow{\mathrm{b}}|=1,|\overrightarrow{\mathrm{c}}|=1$

इसके अतिरिक्त $\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}$

वर्ग करने पर हमें प्राप्त होता है, $$ \begin{aligned} & |\overrightarrow{\mathrm{a}}|^2+|\overrightarrow{\mathrm{b}}|^2+|\overrightarrow{\mathrm{c}}|^2+2(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{c}}+\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{a}})=0 \\ & \Rightarrow 1+1+1+2(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{c}}+\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{a}})=0 \\ & \therefore \overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{c}}+\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{a}}=-\frac{3}{2} $$

\end{aligned} $$

14. यदि कोई भी सदिश $\vec{a}=\overrightarrow{{}0}$ या $\vec{b}=\overrightarrow{{}0}$ है, तो $\vec{a} \cdot \vec{b}=0$। लेकिन विलोम सत्य नहीं हो सकता है। एक उदाहरण के माध्यम से अपने उत्तर की व्याख्या करें।

उत्तर दिखाएं

हल

मान लीजिए $\vec{a}=2 \hat{i}+4 \hat{j}+3 \hat{k}$ और $\vec{b}=3 \hat{i}+3 \hat{j}-6 \hat{k}$ है।

तब,

$\vec{a} \cdot \vec{b}=2.3+4.3+3(-6)=6+12-18=0$

हम अब देखते हैं कि:

$|\vec{a}|=\sqrt{2^{2}+4^{2}+3^{2}}=\sqrt{29}$

$\therefore \vec{a} \neq \overrightarrow{{}0}$

$|\vec{b}|=\sqrt{3^{2}+3^{2}+(-6)^{2}}=\sqrt{54}$

$\therefore \vec{b} \neq \overrightarrow{{}0}$

अतः, दिए गए कथन के विलोम सत्य नहीं हो सकता है।

15. यदि त्रिभुज $ABC$ के शीर्ष $A, B, C$ क्रमशः $(1,2,3),(-1,0,0),(0,1,2)$ हैं, तो $\angle ABC$ ज्ञात कीजिए। [ $\angle ABC$ वेक्टर $\overrightarrow{{}BA}$ और $\overrightarrow{{}BC}$ के बीच का कोण है।]

उत्तर दिखाएं

हल

$\triangle A B C$ के शीर्ष दिए गए हैं $A(1,2,3), B(-1,0,0)$ और $C(0,1,2)$।

इसके अतिरिक्त, दिया गया है कि $\angle ABC$ वेक्टर $\overrightarrow{{}BA}$ और $\overrightarrow{{}BC}$ के बीच का कोण है।

$ \begin{aligned} & \overrightarrow{{}BA}={1-(-1)} \hat{i}+(2-0) \hat{j}+(3-0) \hat{k}=2 \hat{i}+2 \hat{j}+3 \hat{k} \\ & \overrightarrow{{}BC}={0-(-1)} \hat{i}+(1-0) \hat{j}+(2-0) \hat{k}=\hat{i}+\hat{j}+2 \hat{k} \\ & \therefore \overrightarrow{{}BA} \cdot \overrightarrow{{}BC}=(2 \hat{i}+2 \hat{j}+3 \hat{k}) \cdot(\hat{i}+\hat{j}+2 \hat{k})=2 \times 1+2 \times 1+3 \times 2=2+2+6=10 \\ & \mid \overrightarrow{{}BA} \mid=\sqrt{2^{2}+2^{2}+3^{2}}=\sqrt{4+4+9}=\sqrt{17} \\ & \mid \overrightarrow{{}BC} \mid=\sqrt{1+1+2^{2}}=\sqrt{6} \end{aligned} $

अब, यह ज्ञात है कि:

$\overrightarrow{{}BA} \cdot \overrightarrow{{}BC}=|\overrightarrow{{}BA}||\overrightarrow{{}BC}| \cos (\angle ABC)$

$\therefore 10=\sqrt{17} \times \sqrt{6} \cos (\angle ABC)$

$\Rightarrow \cos (\angle ABC)=\frac{10}{\sqrt{17} \times \sqrt{6}}$

$\Rightarrow \angle ABC=\cos ^{-1}(\frac{10}{\sqrt{102}})$

16. सिद्ध कीजिए कि बिंदु $A(1,2,7), B(2,6,3)$ और $C(3,10,-1)$ सरल रेखा पर स्थित हैं।

उत्तर दिखाएं

हल

दिए गए बिंदु $A(1,2,7), B(2,6,3)$ और $C(3,10,-1)$ हैं।

$\therefore \overrightarrow{{}AB}=(2-1) \hat{i}+(6-2) \hat{j}+(3-7) \hat{k}=\hat{i}+4 \hat{j}-4 \hat{k}$

$ \overrightarrow{{}BC}=(3-2) \hat{i}+(10-6) \hat{j}+(-1-3) \hat{k}=\hat{i}+4 \hat{j}-4 \hat{k} $

$\overrightarrow{{}AC}=(3-1) \hat{i}+(10-2) \hat{j}+(-1-7) \hat{k}=2 \hat{i}+8 \hat{j}-8 \hat{k}$

$|\overrightarrow{{}AB}|=\sqrt{1^{2}+4^{2}+(-4)^{2}}=\sqrt{1+16+16}=\sqrt{33}$

$|\overrightarrow{{}BC}|=\sqrt{1^{2}+4^{2}+(-4)^{2}}=\sqrt{1+16+16}=\sqrt{33}$

$|\overrightarrow{{}AC}|=\sqrt{2^{2}+8^{2}+8^{2}}=\sqrt{4+64+64}=\sqrt{132}=2 \sqrt{33}$

$\therefore|\overrightarrow{{}AC}|=|\overrightarrow{{}AB}|+|\overrightarrow{{}BC}|; & |\overrightarrow{{}AC}|=2|\overrightarrow{{}BC}|, |\overrightarrow{{}AC}|=2|\overrightarrow{{}AB}|$

अतः, दिए गए बिंदु A, B और C सरल रेखा पर स्थित हैं।

17. सिद्ध कीजिए कि सदिश $2 \hat{i}-\hat{j}+\hat{k}, \hat{i}-3 \hat{j}-5 \hat{k}$ और $3 \hat{i}-4 \hat{j}-4 \hat{k}$ एक समकोण त्रिभुज के शीर्ष हैं।

उत्तर दिखाएं

हल

मान लीजिए सदिश $2 \hat{i}-\hat{j}+\hat{k}, \hat{i}-3 \hat{j}-5 \hat{k}$ और $3 \hat{i}-4 \hat{j}-4 \hat{k}$ बिंदुओं $A, B$ और $C$ के स्थिति सदिश हैं।

अर्थात, $\overrightarrow{{}OA}=2 \hat{i}-\hat{j}+\hat{k}, \overrightarrow{{}OB}=\hat{i}-3 \hat{j}-5 \hat{k}$ और $\overrightarrow{{}OC}=3 \hat{i}-4 \hat{j}-4 \hat{k}$

अब, सदिश $\overrightarrow{{}AB}, \overrightarrow{{}BC}$ और $\overrightarrow{{}AC}$ त्रिभुज $\triangle ABC$ की भुजाओं को प्रदर्शित करते हैं।

अर्थात, $\overrightarrow{{}OA}=2 \hat{i}-\hat{j}+\hat{k}, \overrightarrow{{}OB}=\hat{i}-3 \hat{j}-5 \hat{k}$ और $\overrightarrow{{}OC}=3 \hat{i}-4 \hat{j}-4 \hat{k}$

$\therefore \overrightarrow{{}AB}=(1-2) \hat{i}+(-3+1) \hat{j}+(-5-1) \hat{k}=-\hat{i}-2 \hat{j}-6 \hat{k}$

$\overrightarrow{{}BC}=(3-1) \hat{i}+(-4+3) \hat{j}+(-4+5) \hat{k}=2 \hat{i}-\hat{j}+\hat{k}$

$\overrightarrow{{}AC}=(3-2) \hat{i}+(-4+1) \hat{j}+(-1-4) \hat{k}=+\hat{i}-3 \hat{j}-5 \hat{k}$

$|\overrightarrow{{}AB}|=\sqrt{(-1)^{2}+(-2)^{2}+(-6)^{2}}=\sqrt{1+4+36}=\sqrt{41}$

$|\overrightarrow{{}BC}|=\sqrt{2^{2}+(-1)^{2}+1^{2}}=\sqrt{4+1+1}=\sqrt{6}$

$|\overrightarrow{{}AC}|=\sqrt{(+1)^{2}+{(-3)^{2}}+(-5)^{2}}=\sqrt{1+9+25}=\sqrt{35}$

$\therefore|\overrightarrow{{}BC}|^{2}+|\overrightarrow{{}AC}|^{2}=6+35=41=|\overrightarrow{{}AB}|^{2}$

इसलिए, $\triangle A B C$ एक समकोण त्रिभुज है।

18. यदि $\vec{a}$ एक गैर-शून्य सदिश है जिसका परिमाण ’ $a$ ’ है और $\lambda$ एक गैर-शून्य अदिश है, तो $\lambda \vec{a}$ एक इकाई सदिश होगा यदि

(A) $\lambda=1$

(B) $\lambda=-1$

(C) $a=|\lambda|$

(D) $a=1 /|\lambda|$

उत्तर दिखाएं

हल

सदिश $\lambda \vec{a}$ एक इकाई सदिश होगा यदि $|\lambda \vec{a}|=1$।

अब,

$|\lambda \vec{a}|=1$

$\Rightarrow|\lambda||\vec{a}|=1$

$\Rightarrow|\vec{a}|=\frac{1}{|\lambda|}$

$[\lambda \neq 0]$

$\Rightarrow a=\frac{1}{|\lambda|}$

$[|\vec{a}|=a]$

इसलिए, सदिश $\lambda \vec{a}$ एक इकाई सदिश होगा यदि $a=\frac{1}{|\lambda|}$। सही उत्तर $D$ है।

10.6.3 दो सदिशों का सदिश (या क्रॉस) गुणनफल

अनुच्छेद 10.2 में, हम तीन आयामी दाएं हाथ के आयताकार निर्देशांक प्रणाली पर चर्चा कर चुके हैं। इस प्रणाली में, जब धनात्मक $x$-अक्ष को गिनती घूमकर धनात्मक $y$-अक्ष में घुमाया जाता है, तो एक दाएं हाथ के मानक बोल्ट धनात्मक $z$-अक्ष की दिशा में आगे बढ़ता है (चित्र 10.22(i))।

एक दाएं हाथ के निर्देशांक प्रणाली में, जब दाएं हाथ के अंगूठे की दिशा धनात्मक $z$-अक्ष की दिशा में होती है, तो अंगूठे के अंगूठे की दिशा धनात्मक $x$-अक्ष से दूर धनात्मक $y$-अक्ष की दिशा में घुमाया जाता है (चित्र 10.22(ii))।

चित्र 10.22

परिभाषा 3 दो गैर-शून्य सदिश $\vec{a}$ और $\vec{b}$ के सदिश गुणनफल को $\vec{a} \times \vec{b}$ से नोट किया जाता है और इसे निम्नलिखित द्वारा परिभाषित किया जाता है

$ \qquad \qquad \qquad\vec{a} \times \vec{b}=|\vec{a} | \vec{b}| \sin \theta \hat{n}, `

$

जहाँ, $\theta$ वेक्टर $\vec{a}$ और $\vec{b}$ के बीच कोण है, $0 \leq \theta \leq \pi$ और $\hat{n}$ एक इकाई वेक्टर है जो $\vec{a}$ और $\vec{b}$ दोनों के लंबवत है, ताकि $\vec{a}, \vec{b}$ और $\hat{n}$ एक दाएं हाथ वाला तंत्र बनाते हैं (चित्र 10.23)। अर्थात, दाएं हाथ वाला तंत्र $\vec{a}$ से $\vec{b}$ की ओर घुमाया जाता है जो $\hat{n}$ की दिशा में चलता है।

चित्र 10.23

यदि $\vec{a}=\overrightarrow{{}0}$ या $\vec{b}=\overrightarrow{{}0}$, तो $\theta$ अनिर्धारित होता है और इस स्थिति में, हम $\vec{a} \times \vec{b}=\overrightarrow{{}0}$ निर्धारित करते हैं।

अवलोकन

1. $\vec{a} \times \vec{b}$ एक वेक्टर है।

2. मान लीजिए $\vec{a}$ और $\vec{b}$ दो गैर-शून्य वेक्टर हैं। तब $\vec{a} \times \vec{b}=\overrightarrow{{}0}$ अगर और केवल अगर $\vec{a}$ और $\vec{b}$ एक दूसरे के समान्तर (या समरेख) हों, अर्थात,

$ \qquad \qquad \qquad\vec{a} \times \vec{b}=\overrightarrow{{}0} \leftrightarrow \vec{a} || \vec{b} $

विशेष रूप से, $\vec{a} \times \vec{a}=\overrightarrow{{}0}$ और $\vec{a} \times(-\vec{a})=\overrightarrow{{}0}$, क्योंकि पहली स्थिति में $\theta=0$ और दूसरी स्थिति में $\theta=\pi$ होता है, जिससे $\sin \theta$ का मान शून्य हो जाता है।

3. यदि $\theta=\dfrac{\pi}{2}$ तो $\vec{a} \times \vec{b}=|\vec{a}||\vec{b}|$ होता है।

4. अवलोकन 2 और 3 के आधार पर, परस्पर लंब इकाई वेक्टर $\hat{i}, \hat{j}$ और $\hat{k}$ (चित्र 10.24) के लिए हम निम्नलिखित प्राप्त करते हैं:

$ \qquad \qquad \qquad\begin{aligned} & \hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=\overrightarrow{{}0} \\ & \hat{i} \times \hat{j}=\hat{k}, \quad \hat{j} \times \hat{k}=\hat{i}, \quad \hat{k} \times \hat{i}=\hat{j} \end{aligned} $

चित्र 10.24

5. सदिश गुणन के अनुसार, दो सदिश $\vec{a}$ और $\vec{b}$ के बीच कोण निम्नलिखित द्वारा दिया जा सकता है

$ \qquad \qquad \qquad \sin \theta=\dfrac{|\vec{a} \times \vec{b}|}{|\vec{a} | \vec{b}|} $

6. सदिश गुणन के असामान्य गुण के कारण, यह हमेशा सत्य होता है कि सदिश गुणन अद्वितीय नहीं होता, क्योंकि $\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}$. वास्तव में, $\vec{a} \times \vec{b}=|\vec{a} | \vec{b}| \sin \theta \hat{n}$, जहाँ $\vec{a}, \vec{b}$ और $\hat{n}$ एक दाएँ हाथ के प्रणाली को बनाते हैं, अर्थात, $\theta$ को $\vec{a}$ से $\vec{b}$ की ओर तय किया जाता है, चित्र 10.25 (i)। वहीं, $\vec{b} \times \vec{a}=|\vec{a} | \vec{b}| \sin \theta \hat{n}_1$, जहाँ $\vec{b}, \vec{a}$ और $\hat{n}_1$ एक दाएँ हाथ के प्रणाली को बनाते हैं, अर्थात, $\theta$ को $\vec{b}$ से $\vec{a}$ की ओर तय किया जाता है, चित्र 10.25(ii)।

चित्र 10.25

इसलिए, यदि हम मान लें कि $\vec{a}$ और $\vec{b}$ कागज के तल में स्थित हैं, तो $\hat{n}$ और $\hat{n}_1$ दोनों कागज के तल के लंबवत होंगे। लेकिन, $\hat{n}$ कागज के ऊपर दिशा में होता है जबकि $\hat{n}_1$ कागज के नीचे दिशा में होता है। अर्थात, $\hat{n}_1=-\hat{n}$।

इसलिए $\qquad \qquad \vec{a} \times \vec{b} =|\vec{a} | \vec{b}| \sin \theta \hat{n}$

$\qquad \qquad \qquad \qquad \quad=-|\vec{a} | \vec{b}| \sin \theta \hat{n}_1=-\vec{b} \times \vec{a}$

7. प्रेक्षण 4 और 6 के आधार पर, हम निम्नलिखित प्राप्त करते हैं

$ \qquad \qquad \qquad\hat{j} \times \hat{i}=-\hat{k}, \quad \hat{k} \times \hat{j}=-\hat{i} \text { और } \hat{i} \times \hat{k}=-\hat{j} \text {. } $

8. यदि $\vec{a}$ और $\vec{b}$ एक त्रिभुज के आसंजित भुजाएँ हों तो इसका क्षेत्रफल $\dfrac{1}{2}|\vec{a} \times \vec{b}|$ द्वारा दिया जाता है।

त्रिभुज के क्षेत्रफल के परिभाषा के आधार पर, चित्र 10.26 से हमें प्राप्त होता है,

त्रिभुज $\mathrm{ABC}$ का क्षेत्रफल $=\dfrac{1}{2} \mathrm{AB} \cdot \mathrm{CD}$।

लेकिन $\mathrm{AB}=|\vec{b}|$ (जैसा कि दिया गया है), और $\mathrm{CD}=|\vec{a}| \sin \theta$।

इसलिए, त्रिभुज $\mathrm{ABC}$ का क्षेत्रफल $=\dfrac{1}{2}|\vec{b} | \vec{a}| \sin \theta=\dfrac{1}{2}|\vec{a} \times \vec{b}|$।

चित्र 10.26

9. यदि $\vec{a}$ और $\vec{b}$ एक समांतर चतुर्भुज के संलग्न भुजाओं को प्रदर्शित करते हैं, तो इसका क्षेत्रफल $|\vec{a} \times \vec{b}|$ द्वारा दिया जाता है।

चित्र 10.27 से, हम निम्नलिखित प्राप्त करते हैं:

समांतर चतुर्भुज $ABCD$ का क्षेत्रफल $AB \cdot DE$ है।

लेकिन $AB=|\vec{b}|$ (जैसा कि दिया गया है), और $CD=|\vec{a}| \sin \theta$ है।

इसलिए,

समांतर चतुर्भुज $ABCD$ का क्षेत्रफल $|\vec{b} | \vec{a}| \sin \theta=|\vec{a} \times \vec{b}|$ है।

चित्र 10.26

हम अब सदिश गुणन के दो महत्वपूर्ण गुणों को बताते हैं।

गुण 3 (सदिश गुणन के योग पर वितरण): यदि $\vec{a}, \vec{b}$ और $\vec{c}$ कोई तीन सदिश हैं और $\lambda$ एक अदिश है, तो

(i) $\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}$

(ii) $\lambda(\vec{a} \times \vec{b})=(\lambda \vec{a}) \times \vec{b}=\vec{a} \times(\lambda \vec{b})$

मान लीजिए कि $\vec{a}$ और $\vec{b}$ दो सदिश हैं जो घटक रूप में $a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ और $b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$ के रूप में दिए गए हैं। तब उनका सदिश गुणन निम्नलिखित द्वारा दिया जा सकता है:

$ \qquad \qquad \qquad\vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} $

स्पष्टीकरण हम निम्नलिखित प्राप्त करते हैं:

$ \qquad \qquad \qquad\begin{aligned} \vec{a} \times \vec{b}= & (a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}) \times(b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}) \\ = & a_1 b_1(\hat{i} \times \hat{i})+a_1 b_2(\hat{i} \times \hat{j})+a_1 b_3(\hat{i} \times \hat{k})+a_2 b_1(\hat{j} \times \hat{i}) \\ & +a_2 b_2(\hat{j} \times \hat{j})+a_2 b_3(\hat{j} \times \hat{k}) \\ & +a_3 b_1(\hat{k} \times \hat{i})+a_3 b_2(\hat{k} \times \hat{j})+a_3 b_3(\hat{k} \times \hat{k}) \qquad \text{(गुण 1 के द्वारा)} \end{aligned} $

= & a_1 b_2(\hat{i} \times \hat{j})-a_1 b_3(\hat{k} \times \hat{i})-a_2 b_1(\hat{i} \times \hat{j}) \\ & +a_2 b_3(\hat{j} \times \hat{k})+a_3 b_1(\hat{k} \times \hat{i})-a_3 b_2(\hat{j} \times \hat{k}) \end{aligned} $

$\qquad $(क्योंकि $\hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=0$ और $\hat{i} \times \hat{k}=-\hat{k} \times \hat{i}, \hat{j} \times \hat{i}=-\hat{i} \times \hat{j}$ और $\hat{k} \times \hat{j}=-\hat{j} \times \hat{k}$ )

$ \qquad \qquad \qquad\qquad \begin{aligned} = & a_1 b_2 \hat{k}-a_1 b_3 \hat{j}-a_2 b_1 \hat{k}+a_2 b_3 \hat{i}+a_3 b_1 \hat{j}-a_3 b_2 \hat{i} \\ & (\text{ क्योंकि } \hat{i} \times \hat{j}=\hat{k}, \hat{j} \times \hat{k}=\hat{i} \text{ और } \hat{k} \times \hat{i}=\hat{j}) \\ = & (a_2 b_3-a_3 b_2) \hat{i}-(a_1 b_3-a_3 b_1) \hat{j}+(a_1 b_2-a_2 b_1) \hat{k} \\ = & \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} \end{aligned} $

उदाहरण 22 यदि $\vec{a}=2 \hat{i}+\hat{j}+3 \hat{k}$ और $\vec{b}=3 \hat{i}+5 \hat{j}-2 \hat{k}$, तो $|\vec{a} \times \vec{b}|$ ज्ञात कीजिए

हल हम जानते हैं

$ \qquad \qquad \qquad\begin{aligned} \vec{a} \times \vec{b} & = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & 3 \\ 3 & 5 & -2 \end{vmatrix} \\ & =\hat{i}(-2-15)-(-4-9) \hat{j}+(10-3) \hat{k}=-17 \hat{i}+13 \hat{j}+7 \hat{k} \end{aligned} $

इसलिए $\qquad \quad|\vec{a} \times \vec{b}|=\sqrt{(-17)^{2}+(13)^{2}+(7)^{2}}=\sqrt{507}$

उदाहरण 23 यदि $\vec{a}=\hat{i}+\hat{j}+\hat{k}, \quad \vec{b}=\hat{i}+2 \hat{j}+3 \hat{k}$, तो ऐसे एक एकक वेक्टर को ज्ञात कीजिए जो वेक्टर $(\vec{a}+\vec{b})$ और $(\vec{a}-\vec{b})$ दोनों पर लम्ब हो

हल हम जानते हैं $\vec{a}+\vec{b}=2 \hat{i}+3 \hat{j}+4 \hat{k}$ और $\vec{a}-\vec{b}=-\hat{j}-2 \hat{k}$

दोनों $\vec{a}+\vec{b}$ और $\vec{a}-\vec{b}$ पर लम्ब एक वेक्टर निम्न द्वारा दिया जाता है

$ \qquad \qquad \qquad(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & 4 \\ 0 & -1 & -2 \end{vmatrix} =-2 \hat{i}+4 \hat{j}-2 \hat{k} \quad(=\vec{c}, \text{ मान लीजिए })

$

अब $ \qquad \qquad \qquad\qquad \qquad|\vec{c}|=\sqrt{4+16+4}=\sqrt{24}=2 \sqrt{6} $

इसलिए, आवश्यक एकक वेक्टर है

$ \qquad \qquad \qquad\qquad\qquad\dfrac{\vec{c}}{|\vec{c}|}=\dfrac{-1}{\sqrt{6}} \hat{i}+\dfrac{2}{\sqrt{6}} \hat{j}-\dfrac{1}{\sqrt{6}} \hat{k} $

ध्यान दें किसी भी तल के लिए दो लम्ब दिशाएँ होती हैं। इसलिए, $\vec{a}+\vec{b}$ और $\vec{a}-\vec{b}$ के लम्ब एकक वेक्टर $\dfrac{1}{\sqrt{6}} \hat{i}-\dfrac{2}{\sqrt{6}} \hat{j}+\dfrac{1}{\sqrt{6}} \hat{k}$ होगा। लेकिन यह $(\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})$ के परिणाम के रूप में होगा।

उदाहरण 24 एक त्रिभुज के क्षेत्रफल को ज्ञात कीजिए जिसके शीर्ष $A(1,1,1), B(1,2,3)$ और $C(2,3,1)$ हैं।

हल हमें $\overrightarrow{{}AB}=\hat{j}+2 \hat{k}$ और $\overrightarrow{{}AC}=\hat{i}+2 \hat{j}$ मिलते हैं। दिए गए त्रिभुज का क्षेत्रफल $\dfrac{1}{2}|\overrightarrow{{}AB} \times \overrightarrow{{}AC}|$ होता है।

अब, $ \qquad \qquad \qquad\overrightarrow{{}AB} \times \overrightarrow{{}AC}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 0 & 1 & 2 \\ 1 & 2 & 0 \end{vmatrix} =-4 \hat{i}+2 \hat{j}-\hat{k} $

इसलिए $ \qquad \qquad \qquad|\overrightarrow{{}AB} \times \overrightarrow{{}AC}|=\sqrt{16+4+1}=\sqrt{21} $

इसलिए, आवश्यक क्षेत्रफल $\dfrac{1}{2} \sqrt{21}$ है।

उदाहरण 25 एक समांतर चतुर्भुज के क्षेत्रफल को ज्ञात कीजिए जिसकी आसन्न भुजाएँ वेक्टरों $\vec{a}=3 \hat{i}+\hat{j}+4 \hat{k}$ और $\vec{b}=\hat{i}-\hat{j}+\hat{k}$ द्वारा दी गई हैं।

हल वेक्टरों $\vec{a}$ और $\vec{b}$ के आसन्न भुजाओं वाले समांतर चतुर्भुज का क्षेत्रफल $|\vec{a} \times \vec{b}|$ द्वारा दिया जाता है।

अब $ \qquad \qquad \qquad\qquad \vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & 1 & 4 \\ 1 & -1 & 1 \end{vmatrix} =5 \hat{i}+\hat{j}-4 \hat{k} $

इसलिए $ \qquad \qquad \qquad|\vec{a} \times \vec{b}|=\sqrt{25+1+16}=\sqrt{42} $

इसलिए, आवश्यक क्षेत्रफल $\sqrt{42}$ है।

अभ्यास 10.4

1. यदि $\vec{a}=\hat{i}-7 \hat{j}+7 \hat{k}$ और $\vec{b}=3 \hat{i}-2 \hat{j}+2 \hat{k}$, तो $|\vec{a} \times \vec{b}|$ ज्ञात कीजिए।

उत्तर दिखाएँ

हल

हम जानते हैं,

$ \begin{aligned} & \vec{a}=\hat{i}-7 \hat{j}+7 \hat{k} \text{ और } \vec{b}=3 \hat{i}-2 \hat{j}+2 \hat{k} \\ & \begin{aligned} \vec{a} \times \vec{b} & = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -7 & 7 \\ 3 & -2 & 2 \end{vmatrix} \\ & =\hat{i}(-14+14)-\hat{j}(2-21)+\hat{k}(-2+21)=19 \hat{j}+19 \hat{k} \end{aligned} \\ & \therefore|\vec{a} \times \vec{b}|=\sqrt{(19)^{2}+(19)^{2}}=\sqrt{2 \times(19)^{2}}=19 \sqrt{2} \end{aligned} $

2. यदि $\vec{a}=3 \hat{i}+2 \hat{j}+2 \hat{k}$ और $\vec{b}=\hat{i}+2 \hat{j}-2 \hat{k}$, तो सदिश $\vec{a}+\vec{b}$ और $\vec{a}-\vec{b}$ के लंब एक एकक सदिश ज्ञात कीजिए।

उत्तर दिखाएँ

हल

हम जानते हैं,

$ \begin{aligned} & \vec{a}=3 \hat{i}+2 \hat{j}+2 \hat{k} \text{ और } \vec{b}=\hat{i}+2 \hat{j}-2 \hat{k} \\ & \therefore \vec{a}+\vec{b}=4 \hat{i}+4 \hat{j}, \vec{a}-\vec{b}=2 \hat{i}+4 \hat{k} \\ & (\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 4 & 4 & 0 \\ 2 & 0 & 4 \end{vmatrix} =\hat{i}(16)-\hat{j}(16)+\hat{k}(-8)=16 \hat{i}-16 \hat{j}-8 \hat{k} \\ & \therefore|(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})|=\sqrt{16^{2}+(-16)^{2}+(-8)^{2}} \\ & =\sqrt{2^{2} \times 8^{2}+2^{2} \times 8^{2}+8^{2}} \\ & =8 \sqrt{2^{2}+2^{2}+1}=8 \sqrt{9}=8 \times 3=24 \end{aligned} $

इसलिए, सदिश $\vec{a}+\vec{b}$ और $\vec{a}-\vec{b}$ के लंब एक एकक सदिश निम्न संबंध द्वारा दिया जाता है,

$= \pm \frac{(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})}{|(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})|}= \pm \frac{16 \hat{i}-16 \hat{j}-8 \hat{k}}{24}$

$= \pm \frac{2 \hat{i}-2 \hat{j}-\hat{k}}{3}= \pm \frac{2}{3} \hat{i} \mp \frac{2}{3} \hat{j} \mp \frac{1}{3} \hat{k}$

3. यदि एक इकाई सदिश $\vec{a}$, $\hat{i}$ से $\frac{\pi}{3}$, $\hat{j}$ से $\frac{\pi}{4}$ और $\hat{k}$ से एक न्यून कोण $\theta$ बनाता है, तो $\theta$ ज्ञात कीजिए और इस प्रकार, $\vec{a}$ के घटक ज्ञात कीजिए।

उत्तर दिखाएं

हल

मान लीजिए इकाई सदिश $\vec{a}$ के घटक $( a_1, a_2, a_3)$ हैं।

$ \vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k} $

क्योंकि $\vec{a}$ एक इकाई सदिश है, इसलिए $|\vec{a}|=1$।

इसके अतिरिक्त, दिया गया है कि $\vec{a}$, $\hat{i}$ से $\frac{\pi}{3}$, $\hat{j}$ से $\frac{\pi}{4}$ और $\hat{k}$ से एक न्यून कोण $\theta$ बनाता है। तब हमें निम्नलिखित मिलता है:

$\cos \frac{\pi}{3}=\frac{a_1}{|\vec{a}|}$

$\Rightarrow \frac{1}{2}=a_1 \quad[|\vec{a}|=1]$

$\cos \frac{\pi}{4}=\frac{a_2}{|\vec{a}|}$

$\Rightarrow \frac{1}{\sqrt{2}}=a_2 \quad[|\vec{a}|=1]$

इसके अतिरिक्त, $\cos \theta=\frac{a_3}{|\vec{a}|}$।

$\Rightarrow a_3=\cos \theta$

अब,

$|a|=1$

$\Rightarrow \sqrt{a_1^{2}+a_2^{2}+a_3^{2}}=1$

$\Rightarrow(\frac{1}{2})^{2}+(\frac{1}{\sqrt{2}})^{2}+\cos ^{2} \theta=1$

$\Rightarrow \frac{1}{4}+\frac{1}{2}+\cos ^{2} \theta=1$

$\Rightarrow \frac{3}{4}+\cos ^{2} \theta=1$

$\Rightarrow \cos ^{2} \theta=1-\frac{3}{4}=\frac{1}{4}$

$\Rightarrow \cos \theta=\frac{1}{2} \Rightarrow \theta=\frac{\pi}{3}$

$\therefore a_3=\cos \frac{\pi}{3}=\frac{1}{2}$

इसलिए, $\theta=\frac{\pi}{3}$ और $\vec{a}$ के घटक $(\frac{1}{2}, \frac{1}{\sqrt{2}}, \frac{1}{2})$ हैं।

4. सिद्ध कीजिए कि

$(\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})=2(\vec{a} \times \vec{b})$

उत्तर दिखाएं

हल

$(\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})$

$=(\vec{a}-\vec{b}) \times \vec{a}+(\vec{a}-\vec{b}) \times \vec{b} \quad$ [सदिश गुणन के योग पर वितरण के गुण का उपयोग करते हुए]

$=\vec{a} \times \vec{a}-\vec{b} \times \vec{a}+\vec{a} \times \vec{b}-\vec{b} \times \vec{b} \quad$ [फिर भी सदिश गुणन के योग पर वितरण के गुण का उपयोग करते हुए]

$=\overrightarrow{{}0}+\vec{a} \times \vec{b}+\vec{a} \times \vec{b}-\overrightarrow{{}0}$

$=2 (\vec{a} \times \vec{b})$

5. यदि $(2 \hat{i}+6 \hat{j}+27 \hat{k}) \times(\hat{i}+\lambda \hat{j}+\mu \hat{k})=\overrightarrow{{}0}$, तो $\lambda$ और $\mu$ ज्ञात कीजिए।

उत्तर दिखाएं

हल

$(2 \hat{i}+6 \hat{j}+27 \hat{k}) \times(\hat{i}+\lambda \hat{j}+\mu \hat{k})=\overrightarrow{{}0}$

$\Rightarrow \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 6 & 27 \\ 1 & \lambda & \mu\end{vmatrix} =0 \hat{i}+0 \hat{j}+0 \hat{k}$

$\Rightarrow \hat{i}(6 \mu-27 \lambda)-\hat{j}(2 \mu-27)+\hat{k}(2 \lambda-6)=0 \hat{i}+0 \hat{j}+0 \hat{k}$

संगत घटकों की तुलना करने पर, हमें प्राप्त होता है:

$6 \mu-27 \lambda=0$

$2 \mu-27=0$

$2 \lambda-6=0$

अब,

$2 \lambda-6=0 \Rightarrow \lambda=3$

$2 \mu-27=0 \Rightarrow \mu=\frac{27}{2}$

अतः, $\lambda=3$ और $\mu=\frac{27}{2}$।

6. यदि $\vec{a} \cdot \vec{b}=0$ और $\vec{a} \times \vec{b}=\overrightarrow{{}0}$, तो आप वेक्टर $\vec{a}$ और $\vec{b}$ के बारे में क्या निष्कर्ष निकाल सकते हैं?

उत्तर दिखाएं

हल

$\vec{a} \cdot \vec{b}=0$

तो,

(i) या तो $|\vec{a}|=0$ है या $|\vec{b}|=0$ है, या $\vec{a} \perp \vec{b}$ (जब $\vec{a}$ और $\vec{b}$ शून्य नहीं हों)

$\vec{a} \times \vec{b}=0$

(ii) या तो $|\vec{a}|=0$ है या $|\vec{b}|=0$ है, या $\vec{a} | \vec{b}$ (जब $\vec{a}$ और $\vec{b}$ शून्य नहीं हों)

लेकिन, $\vec{a}$ और $\vec{b}$ एक साथ लंब और समान्तर नहीं हो सकते।

अतः, $|\vec{a}|=0$ या $|\vec{b}|=0$ है।

7. मान लीजिए वेक्टर $\vec{a}, \vec{b}, \vec{c}$ के रूप में $a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}, b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$, $c_1 \hat{i}+c_2 \hat{j}+c_3 \hat{k}$ दिए गए हैं। फिर दिखाइए कि $\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}$।

उत्तर दिखाएं

हल

हमें दिया गया है,

$\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}, \vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}, \vec{c}=c_1 \hat{i}+c_2 \hat{j}+c_3 \hat{k}$

$(\vec{b}+\vec{c})=(b_1+c_1) \hat{i}+(b_2+c_2) \hat{j}+(b_3+c_3) \hat{k}$

अब, $\vec{a} \times(\vec{b}+\vec{c}) \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1+c_1 & b_2+c_2 & b_3+c_3\end{vmatrix} $

$=\hat{i}[a_2(b_3+c_3)-a_3(b_2+c_2)]-\hat{j}[a_1(b_3+c_3)-a_3(b_1+c_1)]+\hat{k}[a_1(b_2+c_2)-a_2(b_1+c_1)]$

$$=\hat{i}[a_2 b_3+a_2 c_3-a_3 b_2-a_3 c_2]+\hat{j}[-a_1 b_3-a_1 c_3+a_3 b_1+a_3 c_1]+\hat{k}[a_1 b_2+a_1 c_2-a_2 b_1-a_2 c_1] \tag{1}$$

$\vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3\end{vmatrix} $

$$=\hat{i}[a_2 b_3-a_3 b_2]+\hat{j}[b_1 a_3-a_1 b_3]+\hat{k}[a_1 b_2-a_2 b_1] \tag{2}$$

$\vec{a} \times \vec{c}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ c_1 & c_2 & c_3\end{vmatrix} $

$$ \begin{equation*} =\hat{i}[a_2 c_3-a_3 c_2]+\hat{j}[a_3 c_1-a_1 c_3]+\hat{k}[a_1 c_2-a_2 c_1] \tag{3} \end{equation*} $$

(2) और (3) को जोड़ने पर हमें प्राप्त होता है:

$$(\vec{a} \times \vec{b})+(\vec{a} \times \vec{c})=\hat{i}[a_2 b_3+a_2 c_3-a_3 b_2-a_3 c_2]+\hat{j}[b_1 a_3+a_3 c_1-a_1 b_3-a_1 c_3] +\hat{k}[a_1 b_2+a_1 c_2-a_2 b_1-a_2 c_1] \tag{4}$$

अब, (1) और (4) से हमें प्राप्त होता है:

$\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}$

इसलिए, दिए गए परिणाम की सत्यता सिद्ध हो गई है।

8. यदि $\vec{a}=\overrightarrow{{}0}$ या $\vec{b}=\overrightarrow{{}0}$ हो, तो $\vec{a} \times \vec{b}=\overrightarrow{{}0}$. विलोम सत्य है? एक उदाहरण के साथ अपना उत्तर तर्क से समर्थित करें।

उत्तर दिखाएं

Solution

कोई भी समान्तर गैर-शून्य वेक्टर ले लीजिए ताकि $\vec{a} \times \vec{b}=\overrightarrow{{}0}$ हो।

मान लीजिए $\vec{a}=2 \hat{i}+3 \hat{j}+4 \hat{k}, \vec{b}=4 \hat{i}+6 \hat{j}+8 \hat{k}$।

तब,

$\vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & 4 \\ 4 & 6 & 8\end{vmatrix} =\hat{i}(24-24)-\hat{j}(16-16)+\hat{k}(12-12)=0 \hat{i}+0 \hat{j}+0 \hat{k}=\overrightarrow{{}0}$

अब यह देखा जा सकता है कि:

$|\vec{a}|=\sqrt{2^{2}+3^{2}+4^{2}}=\sqrt{29}$

$\therefore \vec{a} \neq \overrightarrow{{}0}$

$|\vec{b}|=\sqrt{4^{2}+6^{2}+8^{2}}=\sqrt{116}$

$\therefore \vec{b} \neq \overrightarrow{{}0}$

इसलिए, दिए गए कथन के विलोम के लिए आवश्यक नहीं है कि यह सत्य हो।

9. त्रिभुज $A(1,1,2), B(2,3,5)$ और $C(1,5,5)$ के शीर्षों वाले त्रिभुज का क्षेत्रफल ज्ञात कीजिए।

उत्तर दिखाएं

हल

त्रिभुज $A B C$ के शीर्ष $A(1,1,2), B(2,3,5)$ और $C(1,5,5)$ दिए गए हैं।

त्रिभुज $ABC$ के समीपस्थ भुजाओं $\overrightarrow{{}AB}$ और $\overrightarrow{{}BC}$ निम्नलिखित हैं:

$ \begin{aligned} & \overrightarrow{{}AB}=(2-1) \hat{i}+(3-1) \hat{j}+(5-2) \hat{k}=\hat{i}+2 \hat{j}+3 \hat{k} \\ & \overrightarrow{{}BC}=(1-2) \hat{i}+(5-3) \hat{j}+(5-5) \hat{k}=-\hat{i}+2 \hat{j} \end{aligned} $

त्रिभुज $ABC$ का क्षेत्रफल $=\frac{1}{2}|\overrightarrow{{}AB} \times \overrightarrow{{}BC}|$

$\overrightarrow{{}AB} \times \overrightarrow{{}BC}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 2 & 3 \\ -1 & 2 & 0\end{vmatrix} =\hat{i}(-6)-\hat{j}(3)+\hat{k}(2+2)=-6 \hat{i}-3 \hat{j}+4 \hat{k}$

$\therefore|\overrightarrow{{}AB} \times \overrightarrow{{}BC}|=\sqrt{(-6)^{2}+(-3)^{2}+4^{2}}=\sqrt{36+9+16}=\sqrt{61}$

अतः, त्रिभुज $A B C$ का क्षेत्रफल $\frac{\sqrt{61}}{2}$ वर्ग इकाई है।

10. सदिशों $\vec{a}=\hat{i}-\hat{j}+3 \hat{k}$ और $\vec{b}=2 \hat{i}-7 \hat{j}+\hat{k}$ द्वारा निर्धारित समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।

उत्तर दिखाएं

हल

सदिशों $\vec{a}$ और $\vec{b}$ द्वारा निर्धारित समांतर चतुर्भुज का क्षेत्रफल $|\vec{a} \times \vec{b}|$ होता है।

समीपस्थ भुजाएँ निम्नलिखित हैं:

$\vec{a}=\hat{i}-\hat{j}+3 \hat{k}$ और $\vec{b}=2 \hat{i}-7 \hat{j}+\hat{k}$

$\therefore \vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -1 & 3 \\ 2 & -7 & 1\end{vmatrix} =\hat{i}(-1+21)-\hat{j}(1-6)+\hat{k}(-7+2)=20 \hat{i}+5 \hat{j}-5 \hat{k}$

$|\vec{a} \times \vec{b}|=\sqrt{20^{2}+5^{2}+5^{2}}=\sqrt{400+25+25}=15 \sqrt{2}$

अतः, दिए गए समांतर चतुर्भुज का क्षेत्रफल $15 \sqrt{2}$ वर्ग इकाई है।

11. ऐसे सदिश $\vec{a}$ और $\vec{b}$ मान लीजिए जिनके $|\vec{a}|=3$ और $|\vec{b}|=\frac{\sqrt{2}}{3}$ हैं, तो $\vec{a} \times \vec{b}$ एक इकाई सदिश होगा, यदि $\vec{a}$ और $\vec{b}$ के बीच कोण है

(A) $\pi / 6$

(B) $\pi / 4$

(C) $\pi / 3$

(D) $\pi / 2$

उत्तर दिखाएं

हल

दिया गया है $|\vec{a}|=3$ और $|\vec{b}|=\frac{\sqrt{2}}{3}$।

हम जानते हैं कि $\vec{a} \times \vec{b}=|\vec{a}||\vec{b}| \sin \theta \hat{n}$, जहाँ $\hat{n}$ एक इकाई सदिश है जो $\vec{a}$ और $\vec{b}$ दोनों के लंबवत है और $\theta$ $\vec{a}$ और $\vec{b}$ के बीच का कोण है।

अब, $\vec{a} \times \vec{b}$ एक इकाई सदिश होगा यदि $|\vec{a} \times \vec{b}|=1$।

$|\vec{a} \times \vec{b}|=1$

$\Rightarrow|| \vec{a}|| \vec{b}|\sin \theta \hat{n}|=1$

$\Rightarrow|\vec{a}||\vec{b}||\sin \theta|=1$

$\Rightarrow 3 \times \frac{\sqrt{2}}{3} \times \sin \theta=1$

$\Rightarrow \sin \theta=\frac{1}{\sqrt{2}}$

$\Rightarrow \theta=\frac{\pi}{4}$

अतः, $\vec{a} \times \vec{b}$ एक इकाई सदिश होगा यदि $\vec{a}$ और $\vec{b}$ के बीच का कोण $\frac{\pi}{4}$ हो।

सही उत्तर है $B$।

12. आयत के क्षेत्रफल का परिकलन कीजिए जिसके शीर्ष $A, B, C$ और $D$ के स्थिति सदिश क्रमशः $-\hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}, \hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}, \hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}$ और $-\hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}$ हैं।

(A) $\frac{1}{2}$

(B) 1

(C) 2

(D) 4

उत्तर दिखाएं

हल

आयत $ABCD$ के शीर्ष $A, B, C$ और $D$ के स्थिति सदिश निम्नलिखित हैं:

$\overrightarrow{{}OA}=-\hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}, \overrightarrow{{}OB}=\hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}, \overrightarrow{{}OC}=\hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}, \overrightarrow{{}OD}=-\hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}$

दिए गए आयत के आसन्न भुजाएँ $\overrightarrow{{}AB}$ और $\overrightarrow{{}BC}$ निम्नलिखित हैं:

$ \begin{aligned} & \overrightarrow{{}AB}=\overrightarrow{{}OB}-\overrightarrow{{}OA} =(1+1) \hat{i}+(\frac{1}{2}-\frac{1}{2}) \hat{j}+(4-4) \hat{k}=2 \hat{i} \\ & \overrightarrow{{}BC}=\overrightarrow{{}OC}-\overrightarrow{{}OB}=(1-1) \hat{i}+(-\frac{1}{2}-\frac{1}{2}) \hat{j}+(4-4) \hat{k}=-\hat{j} \\

& \therefore \overrightarrow{{}AB} \times \overrightarrow{{}BC}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 0 & 0 \\ 0 & -1 & 0 \end{vmatrix} =\hat{k}(-2)=-2 \hat{k} \\ & |\overrightarrow{{}AB} \times \overrightarrow{{}AC}|=\sqrt{(-2)^{2}}=2 \end{aligned} $

अब, यह ज्ञात है कि एक समांतर चतुर्भुज के क्षेत्रफल के लिए, जिसकी आसन्न भुजाएँ $\vec{a}$ और $\vec{b}$ हों, वह $|\vec{a} \times \vec{b}|$ होता है।

इसलिए, दिए गए आयत का क्षेत्रफल $|\overrightarrow{{}AB} \times \overrightarrow{{}BC}|=2$ वर्ग इकाई है। सही उत्तर $C$ है।

अन्य उदाहरण

उदाहरण 26 XY-तल में सभी एकक वेक्टर लिखिए।

हल मान लीजिए $\vec{r}=x \hat{i}+y \hat{j}$ एक XY-तल में एकक वेक्टर है (चित्र 10.28)। तब, चित्र से हमें $x=\cos \theta$ और $y=\sin \theta$ (क्योंकि $|\vec{r}|=1$) मिलता है। इसलिए, हम वेक्टर $\vec{r}$ को लिख सकते हैं

$ \qquad \qquad \qquad \vec{r}(=\overrightarrow{{}OP})=\cos \theta \hat{i}+\sin \theta \hat{j} \hspace{2cm} \ldots(1) $

स्पष्ट रूप से, $ \qquad \qquad \qquad|\vec{r}|=\sqrt{\cos ^{2} \theta+\sin ^{2} \theta}=1 $

चित्र 10.28

इसके अतिरिक्त, जब $\theta$ 0 से $2 \pi$ तक बदलता है, तो बिंदु $P$ (चित्र 10.28) वृत्त $x^{2}+y^{2}=1$ के अनुसार वृत्त के अंदर गति करता है जो वृत्त के बाहर घूमता है और इस प्रकार सभी संभावित दिशाओं को ढकता है। इसलिए, (1) द्वारा XY-तल में सभी एकक वेक्टर प्राप्त होते हैं।

उदाहरण 27 यदि $\hat{i}+\hat{j}+\hat{k}, 2 \hat{i}+5 \hat{j}, 3 \hat{i}+2 \hat{j}-3 \hat{k}$ और $\hat{i}-6 \hat{j}-\hat{k}$ बिंदुओं $A, B, C$ और $D$ के स्थिति वेक्टर हैं, तो $\overrightarrow{{}AB}$ और $\overrightarrow{{}CD}$ के बीच कोण ज्ञात कीजिए। निष्कर्ष लगाइए कि $\overrightarrow{{}AB}$ और $\overrightarrow{{}CD}$ संरेख हैं।

हल ध्यान दें कि यदि $\theta$ $A B$ और $C D$ के बीच कोण है, तो $\theta$ भी $\overrightarrow{{}AB}$ और $\overrightarrow{{}CD}$ के बीच कोण है।

अब $ \qquad \qquad \qquad\overrightarrow{{}AB} =\text{ स्थिति वेक्टर } B-\text{ स्थिति वेक्टर } A$

$\qquad \qquad \qquad\qquad\qquad=(2 \hat{i}+5 \hat{j})-(\hat{i}+\hat{j}+\hat{k})=\hat{i}+4 \hat{j}-\hat{k}$

इसलिए $ \qquad \qquad \qquad|\overrightarrow{{}AB}|=\sqrt{(1)^{2}+(4)^{2}+(-1)^{2}}=3 \sqrt{2} $

इसी तरह $ \qquad \qquad \qquad\overrightarrow{{}CD}=-2 \hat{i}-8 \hat{j}+2 \hat{k} \text{ और }|\overrightarrow{{}CD}|=6 \sqrt{2} $

इसलिए $ \qquad \qquad \qquad\cos \theta =\dfrac{\overrightarrow{{}AB} \cdot \overrightarrow{{}CD}}{|\overrightarrow{{}AB}||\overrightarrow{{}CD}|} $

$ \qquad \qquad \qquad \qquad =\dfrac{1(-2)+4(-8)+(-1)(2)}{(3 \sqrt{2})(6 \sqrt{2})}=\dfrac{-36}{36}=-1 $

क्योंकि $0 \leq \theta \leq \pi$, इसलिए $\theta=\pi$ होता है। यह दिखाता है कि $\overrightarrow{{}A B}$ और $\overrightarrow{{}C D}$ संरेख हैं।

अलग-अलग तरीके से, $~\overrightarrow{{}AB}=-\dfrac{1}{2} \overrightarrow{{}CD}$ जिससे यह निष्कर्ष निकलता है कि $\overrightarrow{{}AB}$ और $\overrightarrow{{}CD}$ संरेख सदिश हैं।

उदाहरण 28 मान लीजिए $\vec{a}, \vec{b}$ और $\vec{c}$ तीन सदिश हैं जैसे कि $|\vec{a}|=3,|\vec{b}|=4,|\vec{c}|=5$ और इनमें से प्रत्येक दूसरे दो के योग के लंब है, तो $|\vec{a}+\vec{b}+\vec{c}|$ का मान ज्ञात कीजिए।

हल दिया गया है $\vec{a} \cdot(\vec{b}+\vec{c})=0, \vec{b} \cdot(\vec{c}+\vec{a})=0, \vec{c} \cdot(\vec{a}+\vec{b})=0$।

अब $ \qquad \qquad \quad|\vec{a}+\vec{b}+\vec{c}|^{2}= (\vec{a}+\vec{b}+\vec{c})^{2}=(\vec{a}+\vec{b}+\vec{c}) \cdot(\vec{a}+\vec{b}+\vec{c}) $

$\qquad \qquad \qquad\qquad \qquad \qquad= \vec{a} \cdot \vec{a}+\vec{a} \cdot(\vec{b}+\vec{c})+\vec{b} \cdot \vec{b}+\vec{b} \cdot(\vec{a}+\vec{c})+\vec{c} \cdot(\vec{a}+\vec{b})+\vec{c} \cdot \vec{c}$

$\qquad \qquad \qquad\qquad \qquad \qquad= |\vec{a}|^{2}+|\vec{b}|^{2}+|\vec{c}|^{2}$

$\qquad \qquad \qquad\qquad \qquad \qquad= 9+16+25=50$

इसलिए $ \qquad \qquad \quad |\vec{a}+\vec{b}+\vec{c}|=\sqrt{50}=5 \sqrt{2} $

उदाहरण 29 तीन सदिश $\vec{a}, \vec{b}$ और $\vec{c}$ इस शर्त को संतुष्ट करते हैं कि $\vec{a}+\vec{b}+\vec{c}=\overrightarrow{{}0}$। मात्रा $\mu=\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}$ का मान ज्ञात कीजिए, यदि $|\vec{a}|=3,|\vec{b}|=4$ और $|\vec{c}|=2$ है।

हल क्योंकि $\vec{a}+\vec{b}+\vec{c}=\overrightarrow{{}0}$, हमें इस प्रकार मिलता है

$ \qquad \qquad \qquad\vec{a}+\vec{b}+\vec{c}=\overrightarrow{{}0}=0$

या $ \qquad \qquad \quad\vec{a} \cdot \vec{a}+\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}=0 $

इसलिए $ \qquad \qquad \quad\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}=-|\vec{a}|^{2}=-9 \hspace{3cm} \ldots(1) $

फिर,

Again, $ \qquad \qquad \quad\vec{b} \cdot \vec{b}+\vec{b} \cdot \vec{a}+\vec{b} \cdot \vec{c}=0 $

or $ \qquad \qquad \quad\vec{b} \cdot \vec{a}+\vec{b} \cdot \vec{c}=-|\vec{b}|^{2}=-16 \hspace{3cm} \ldots(2) $

Similarly, $ \qquad \qquad \quad\vec{c} \cdot \vec{c}+\vec{c} \cdot \vec{a}+\vec{c} \cdot \vec{b}=0 $

or $ \qquad \qquad \quad\vec{c} \cdot \vec{a}+\vec{c} \cdot \vec{b}=-|\vec{c}|^{2}=-4 \hspace{3cm} \ldots(3) $

Adding equations (1), (2), and (3), we get $ \qquad \qquad \quad 2(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}) = -9 -16 -4 = -29 $

Therefore, $ \qquad \qquad \quad \vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a} = -\dfrac{29}{2} $

Hence, $\mu = -\dfrac{29}{2}$.

$ \qquad \qquad \quad\vec{b} \cdot(\vec{a}+\vec{b}+\vec{c})=0 $

या $ \qquad \qquad \quad\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}=-|\vec{b}|^{2}=-16 \hspace{3cm} \ldots(2) $

इसी तरह $ \qquad \qquad \quad\vec{a} \cdot \vec{c}+\vec{b} \cdot \vec{c}=-4 \hspace{3cm} \ldots(3) $

(1), (2) और (3) को जोड़ने पर हमें प्राप्त होता है

$ \qquad \qquad \quad2(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{a} \cdot \vec{c})=-29 $

$ \qquad \qquad \quad 2 \mu=-29, \text{ अर्थात } \mu=\dfrac{-29}{2} $

उदाहरण 30 यदि आपेक्षिक दायें हाथ के परस्पर लम्ब एकक वेक्टरों $ \hat {i}, \hat {j} $ और $ \hat {k} $ के तंत्र के संदर्भ में, $ \vec{\alpha}=3 \hat {i} - \hat {j}, \vec{\beta}=2 \hat {i} + \hat {j} - 3 \hat {k} $, तो $ \vec{\beta} $ को $ \vec{\beta} _ {1} + \vec{\beta} _ {2} $ के रूप में व्यक्त कीजिए, जहाँ $ \vec{\beta} _ {1} $, $ \vec{\alpha} $ के समानुपाती है और $ \vec{\beta} _ {2} $, $ \vec{\alpha} $ के लम्बवत है।

हल मान लीजिए $ \vec{\beta} _ {1} =\lambda \vec{\alpha}, \lambda $ एक अदिश है, अर्थात $ \vec{\beta} _ {1} = 3 \lambda \hat {i} - \lambda \hat {j} $।

अब $ \qquad \qquad \quad\vec{\beta} _ {2}=\vec{\beta}-\vec{\beta} _ {1}=(2-3 \lambda) \hat{i}+(1+\lambda) \hat{j}-3 \hat{k} $

अब, क्योंकि $\vec{\beta} _ {2}$, $\vec{\alpha}$ के लम्बवत होना चाहिए, हमें $\vec{\alpha} \cdot \vec{\beta} _ {2}=0$ होना चाहिए। अर्थात,

$ \qquad \qquad \quad 3(2-3 \lambda)-(1+\lambda)=0 $

या $ \qquad \qquad \quad \lambda=\dfrac{1}{2} $

इसलिए $ \qquad \qquad \quad \vec{\beta} _{1}=\dfrac{3}{2} \hat{i}-\dfrac{1}{2} \hat{j} ~\text { और } ~\vec{\beta} _{2}=\dfrac{1}{2} \hat{i}+\dfrac{3}{2} \hat{j}-3 \hat{k} $

अध्याय 10 पर अतिरिक्त अभ्यास

1. $30^{\circ}$ कोण बनाते हुए $x$-अक्ष के धनात्मक दिशा के साथ एक एकक सदिश लिखिए जो $XY$-तल में हो।

उत्तर दिखाएं

हल

यदि $\vec{r}$ $X Y$-तल में एक एकक सदिश है, तो $\vec{r}=\cos \theta \hat{i}+\sin \theta \hat{j}$।

यहाँ, $\theta$ एकक सदिश के $x$-अक्ष के धनात्मक दिशा के साथ बनाये गए कोण है।

इसलिए, $\theta=30^{\circ}$ के लिए:

$\vec{r}=\cos 30^{\circ} \hat{i}+\sin 30^{\circ} \hat{j}=\dfrac{\sqrt{3}}{2} \hat{i}+\dfrac{1}{2} \hat{j}$

अतः, आवश्यक एकक सदिश $\dfrac{\sqrt{3}}{2} \hat{i}+\dfrac{1}{2} \hat{j}$ है।

2. बिंदुओं $P(x _ {1}, y _ {1}, z _ {1})$ और $Q(x _ {2}, y _ {2}, z _ {2})$ को जोड़ने वाले सदिश के अदिश घटक और परिमाण ज्ञात कीजिए।

उत्तर दिखाएं

हल

बिंदुओं $P(x_1, y_1, z_1)$ और $Q(x_2, y_2, z_2)$ को जोड़ने वाले सदिश को इस प्रकार प्राप्त किया जा सकता है, $\overrightarrow{{}PQ}=$ $Q$ का स्थिति सदिश - $P$ का स्थिति सदिश

$ =(x_2-x_1) \hat{i}+(y_2-y_1) \hat{j}+(z_2-z_1) \hat{k} $

$ |\overrightarrow{{}PQ}|=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}} $

अतः, दिए गए बिंदुओं को जोड़ने वाले सदिश के अदिश घटक और उसके परिमाण क्रमशः ${(x_2-x_1),(y_2-y_1),(z_2-z_1)}$ और $\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}}$ हैं।

3. एक लड़की पश्चिम की ओर 4 किमी चलती है, फिर उसके उत्तर की ओर 30° पूर्व की दिशा में 3 किमी चलती है और रुक जाती है। लड़की के अपने प्रारंभिक बिंदु से विस्थापन की गणना कीजिए।

उत्तर दिखाएं

हल

मान लीजिए $O$ और $B$ क्रमशः लड़की के प्रारंभिक और अंतिम स्थिति हैं। तब, लड़की की स्थिति इस प्रकार दर्शाई जा सकती है:

अब, हमारे पास है:

$$ \begin{aligned} \overrightarrow{{}OA} & =-4 \hat{i} \\ \overrightarrow{{}AB} & =\hat{i}|\overrightarrow{{}AB}| \cos 60^{\circ}+\hat{j}|\overrightarrow{{}AB}| \sin 60^{\circ} \\ & =\hat{i} 3 \times \dfrac{1}{2}+\hat{j} 3 \times \dfrac{\sqrt{3}}{2} \\ & =\dfrac{3}{2} \hat{i}+\dfrac{3 \sqrt{3}}{2} \hat{j} \end{aligned} $$

त्रिभुज के वेक्टर जोड़ के नियम के अनुसार, हमारे पास है:

$$ \begin{aligned} \overrightarrow{{}OB} & =\overrightarrow{{}OA}+\overrightarrow{{}AB} \\ & =(-4 \hat{i})+(\dfrac{3}{2} \hat{i}+\dfrac{3 \sqrt{3}}{2} \hat{j}) \\ & =(-4+\dfrac{3}{2}) \hat{i}+\dfrac{3 \sqrt{3}}{2} \hat{j} \\ & =(\dfrac{-8+3}{2}) \hat{i}+\dfrac{3 \sqrt{3}}{2} \hat{j} \\ & =\dfrac{-5}{2} \hat{i}+\dfrac{3 \sqrt{3}}{2} \hat{j} \end{aligned} $$

इसलिए, लड़की के अपने प्रारंभिक बिंदु से विस्थापन है

$$ \dfrac{-5}{2} \hat{i}+\dfrac{3 \sqrt{3}}{2} \hat{j} $$

4. यदि $\vec{a}=\vec{b}+\vec{c}$, तो $|\vec{a}|=|\vec{b}|+|\vec{c}|$ के लिए क्या सत्य है? अपने उत्तर की व्याख्या करें।

उत्तर दिखाएं

हल

$\triangle ABC$ में, मान लीजिए $\overrightarrow{{}CB}=\vec{a}, \overrightarrow{{}CA}=\vec{b}$, और $\overrightarrow{{}AB}=\vec{c}$ (जैसा कि नीचे दिए गए चित्र में दिखाया गया है)।

अब, वेक्टर जोड़ के त्रिभुज नियम के अनुसार, हमारे पास $\vec{a}=\vec{b}+\vec{c}$ है।

यह स्पष्ट रूप से ज्ञात है कि $|\vec{a}|,|\vec{b}|$, और $|\vec{c}|$ $\triangle ABC$ के तीनों भुजाओं को प्रदर्शित करते हैं।

इसके अतिरिक्त, यह ज्ञात है कि त्रिभुज की किन्ही दो भुजाओं की लंबाई का योग तीसरी भुजा की लंबाई से अधिक होता है।

$\therefore|\vec{a}|<|\vec{b}|+|\vec{c}|$

मान लीजिए $\vec a = 2\hat i +2\hat j+2\hat k, \vec b= -\hat i+\hat j+ 0 \hat k, \vec c=3\hat i +\hat j+2\hat k$

$\vec b+ \vec c = 2\hat i +2\hat j+2\hat k=\vec a$

$\Rightarrow \vec a = \vec b + \vec c$

अब

$|\vec a|= \sqrt{2^2+2^2+2^2}=\sqrt{12}$

$|\vec b |= \sqrt{1+1}=\sqrt{2}$

$|\vec c|= \sqrt{9+1+4}=\sqrt{14}$

$|\vec b|+|\vec c|=\sqrt{2}+\sqrt{14} $

$|\vec a|=\sqrt{12}$

$\therefore \sqrt{12}\neq \sqrt{2}+ \sqrt{14}$

इसलिए, $|\vec{a}|=|\vec{b}|+|\vec{c}|$ के लिए यह सत्य नहीं है।

5. ज्ञात कीजिए $x$ का मान जिसके लिए $x(\hat{i}+\hat{j}+\hat{k})$ एक इकाई सदिश हो।

उत्तर दिखाएं

हल

यदि $x(\hat{i}+\hat{j}+\hat{k})$ एक इकाई सदिश है तो $|x(\hat{i}+\hat{j}+\hat{k})|=1$ होगा।

अब,

$|x(\hat{i}+\hat{j}+\hat{k})|=1$

$\Rightarrow \sqrt{x^{2}+x^{2}+x^{2}}=1$

$\Rightarrow \sqrt{3 x^{2}}=1$

$\Rightarrow \sqrt{3} x=1$

$\Rightarrow x= \pm \dfrac{1}{\sqrt{3}}$

इसलिए, $x$ के अभीष्ट मान के लिए $x= \pm \dfrac{1}{\sqrt{3}}$ है।

6. सदिश $\vec{a}=2 \hat{i}+3 \hat{j}-\hat{k}$ और $\vec{b}=\hat{i}-2 \hat{j}+\hat{k}$ के परिणामी के समान्तर एक सदिश ज्ञात कीजिए जिसका परिमाण 5 इकाई हो।

उत्तर दिखाएं

हल

हम जानते हैं,

$\vec{a}=2 \hat{i}+3 \hat{j}-\hat{k}$ और $\vec{b}=\hat{i}-2 \hat{j}+\hat{k}$

मान लीजिए $\vec{c}$, $\vec{a}$ और $\vec{b}$ के परिणामी है।

तब,

$\vec{c}=\vec{a}+\vec{b}=(2+1) \hat{i}+(3-2) \hat{j}+(-1+1) \hat{k}=3 \hat{i}+\hat{j}$

$\therefore|\vec{c}|=\sqrt{3^{2}+1^{2}}=\sqrt{9+1}=\sqrt{10}$

$\therefore \hat{c}=\dfrac{\vec{c}}{|\vec{c}|}=\dfrac{(3 \hat{i}+\hat{j})}{\sqrt{10}}$

इसलिए, सदिश $\vec{a}$ और $\vec{b}$ के परिणामी के समान्तर एक सदिश जिसका परिमाण 5 इकाई हो इसका मान है

$ 5 \cdot \hat{c}= 5 \cdot \dfrac{1}{\sqrt{10}}(3 \hat{i}+\hat{j})= \dfrac{3 \sqrt{10} }{2}\hat{i} + \dfrac{\sqrt{10}}{2} \hat{j}$.

7. यदि $\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=2 \hat{i}-\hat{j}+3 \hat{k}$ और $\vec{c}=\hat{i}-2 \hat{j}+\hat{k}$, तो सदिश $2 \vec{a}-\vec{b}+3 \vec{c}$ के समान्तर एक इकाई सदिश ज्ञात कीजिए।

उत्तर दिखाएं

हल

हम जानते हैं,

$ \begin{aligned} & \vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=2 \hat{i}-\hat{j}+3 \hat{k} \text{ और } \vec{c}=\hat{i}-2 \hat{j}+\hat{k} \\

$$ \begin{aligned} 2 \vec{a}-\vec{b}+3 \vec{c} & =2(\hat{i}+\hat{j}+\hat{k})-(2 \hat{i}-\hat{j}+3 \hat{k})+3(\hat{i}-2 \hat{j}+\hat{k}) \\ & =2 \hat{i}+2 \hat{j}+2 \hat{k}-2 \hat{i}+\hat{j}-3 \hat{k}+3 \hat{i}-6 \hat{j}+3 \hat{k} \\ & =3 \hat{i}-3 \hat{j}+2 \hat{k} \end{aligned} \\ & \begin{aligned} |2 \vec{a}-\vec{b}+3 \vec{c}| & =\sqrt{3^{2}+(-3)^{2}+2^{2}}=\sqrt{9+9+4}=\sqrt{22} \end{aligned} \end{aligned} $$

अतः, $2 \vec{a}-\vec{b}+3 \vec{c}$ के अनुदिश एक इकाई सदिश है

$$ \dfrac{2 \vec{a}-\vec{b}+3 \vec{c}}{|2 \vec{a}-\vec{b}+3 \vec{c}|}=\dfrac{3 \hat{i}-3 \hat{j}+2 \hat{k}}{\sqrt{22}}=\dfrac{3}{\sqrt{22}} \hat{i}-\dfrac{3}{\sqrt{22}} \hat{j}+\dfrac{2}{\sqrt{22}} \hat{k} $$

8. सिद्ध कीजिए कि बिंदु $A(1,-2,-8), B(5,0,-2)$ और $C(11,3,7)$ संरेख हैं, और $B$ द्वारा $AC$ को किस अनुपात में विभाजित किया जाता है।

उत्तर दिखाएं

हल

दिए गए बिंदु $A(1,-2,-8), B(5,0,-2)$ और $C(11,3,7)$ हैं।

$\therefore \overrightarrow{{}AB}=(5-1) \hat{i}+(0+2) \hat{j}+(-2+8) \hat{k}=4 \hat{i}+2 \hat{j}+6 \hat{k}$

$$ \overrightarrow{{}BC}=(11-5) \hat{i}+(3-0) \hat{j}+(7+2) \hat{k}=6 \hat{i}+3 \hat{j}+9 \hat{k} $$

$\overrightarrow{{}AC}=(11-1) \hat{i}+(3+2) \hat{j}+(7+8) \hat{k}=10 \hat{i}+5 \hat{j}+15 \hat{k}$

$|\overrightarrow{{}AB}|=\sqrt{4^{2}+2^{2}+6^{2}}=\sqrt{16+4+36}=\sqrt{56}=2 \sqrt{14}$

$|\overrightarrow{{}BC}|=\sqrt{6^{2}+3^{2}+9^{2}}=\sqrt{36+9+81}=\sqrt{126}=3 \sqrt{14}$

$|\overrightarrow{{}AC}|=\sqrt{10^{2}+5^{2}+15^{2}}=\sqrt{100+25+225}=\sqrt{350}=5 \sqrt{14}$

$\therefore|\overrightarrow{{}AC}|=|\overrightarrow{{}AB}|+|\overrightarrow{{}BC}|$

अतः, दिए गए बिंदु $A, B$ और $C$ संरेख हैं।

अब, मान लीजिए बिंदु $B$ बिंदु $AC$ को $\lambda: 1$ के अनुपात में विभाजित करता है। तब हमें निम्न प्राप्त होता है:

$$ \begin{aligned} & \overrightarrow{{}OB}=\dfrac{\lambda \overrightarrow{{}OC}+\overrightarrow{{}OA}}{(\lambda+1)} \\ & \Rightarrow 5 \hat{i}-2 \hat{k}=\dfrac{\lambda(11 \hat{i}+3 \hat{j}+7 \hat{k})+(\hat{i}-2 \hat{j}-8 \hat{k})}{\lambda+1} \\ & \Rightarrow(\lambda+1)(5 \hat{i}-2 \hat{k})=11 \lambda \hat{i}+3 \lambda \hat{j}+7 \lambda \hat{k}+\hat{i}-2 \hat{j}-8 \hat{k} \\ $$

$$ \Rightarrow 5(\lambda+1) \hat{i}-2(\lambda+1) \hat{k}=(11 \lambda+1) \hat{i}+(3 \lambda-2) \hat{j}+(7 \lambda-8) \hat{k} $$ $$ \end{aligned} $$

$$ $ $$

संगत घटकों के तुलना करने पर, हम प्राप्त करते हैं:

$$5(\lambda+1)=11 \lambda+1$$

$$ \Rightarrow 5 \lambda+5=11 \lambda+1 $$

$$ \Rightarrow 6 \lambda=4 $$

$$ \Rightarrow \lambda=\dfrac{4}{6}=\dfrac{2}{3} $$

इसलिए, बिंदु $B$ बिंदुओं $A$ और $C$ को $2: 3$ के अनुपात में विभाजित करता है।

9. बिंदुओं $P$ और $Q$ के स्थिति सदिश $(2 \vec{a}+\vec{b})$ और $(\vec{a}-3 \vec{b})$ को जोड़ने वाली रेखा के बाहरी बिंदु $R$ का स्थिति सदिश ज्ञात कीजिए जो बिंदुओं $P$ और $Q$ को $1: 2$ के अनुपात में विभाजित करता है। इसके अलावा, दिखाइए कि $P$ रेखाखंड $RQ$ का मध्य बिंदु है।

उत्तर दिखाएं

हल

दिया गया है कि $\overrightarrow{{}OP}=2 \vec{a}+\vec{b}, \overrightarrow{{}OQ}=\vec{a}-3 \vec{b}$।

दिया गया है कि बिंदु $R$ बिंदुओं $P$ और $Q$ को $1: 2$ के अनुपात में बाहरी विभाजित करता है। तब, खंडन सूत्र का उपयोग करने पर हम प्राप्त करते हैं:

$$ \overrightarrow{{}OR}=\dfrac{2(2 \vec{a}+\vec{b})-(\vec{a}-3 \vec{b})}{2-1}=\dfrac{4 \vec{a}+2 \vec{b}-\vec{a}+3 \vec{b}}{1}=3 \vec{a}+5 \vec{b} $$

इसलिए, बिंदु $R$ का स्थिति सदिश $3 \vec{a}+5 \vec{b}$ है।

रेखाखंड $RQ$ के मध्य बिंदु का स्थिति सदिश:

$$ \dfrac{\overrightarrow{{}OQ}+\overrightarrow{{}OR}}{2} $$

$$ =\dfrac{(\vec{a}-3 \vec{b})+(3 \vec{a}+5 \vec{b})}{2} $$

$$ =2 \vec{a}+\vec{b} $$

$$ =\overrightarrow{{}OP} $$

इसलिए, $P$ रेखाखंड $RQ$ का मध्य बिंदु है।

10. एक समांतर चतुर्भुज के दो आसन्न भुजाएँ $2 \hat{i}-4 \hat{j}+5 \hat{k}$ और $\hat{i}-2 \hat{j}-3 \hat{k}$ हैं। इसके विकर्ण के समांतर एक एकक सदिश ज्ञात कीजिए। इसके क्षेत्रफल को भी ज्ञात कीजिए।

उत्तर दिखाएं

हल

एक समांतर चतुर्भुज के आसन्न भुजाएँ दी गई हैं: $\vec{a}=2 \hat{i}-4 \hat{j}+5 \hat{k}$ और $\vec{b}=\hat{i}-2 \hat{j}-3 \hat{k}$

तब, समांतर चतुर्भुज के विकर्ण को $\vec{a}+\vec{b}$ द्वारा दिया जाता है।

$$ \vec{a}+\vec{b}=(2+1) \hat{i}+(-4-2) \hat{j}+(5-3) \hat{k}=3 \hat{i}-6 \hat{j}+2 \hat{k} $$

इसलिए, विकर्ण के समान्तर एक एकक सदिश है

$ \dfrac{\vec{a}+\vec{b}}{|\vec{a}+\vec{b}|}=\dfrac{3 \hat{i}-6 \hat{j}+2 \hat{k}}{\sqrt{3^{2}+(-6)^{2}+2^{2}}}=\dfrac{3 \hat{i}-6 \hat{j}+2 \hat{k}}{\sqrt{9+36+4}}=\dfrac{3 \hat{i}-6 \hat{j}+2 \hat{k}}{7}=\dfrac{3}{7} \hat{i}-\dfrac{6}{7} \hat{j}+\dfrac{2}{7} \hat{k} . $

$\therefore$ समांतर चतुर्भुज $ABCD$ का क्षेत्रफल $|\vec{a} \times \vec{b}|$

$ \begin{aligned} & \vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -4 & 5 \\ 1 & -2 & -3 \end{vmatrix} \\ &=\hat{i}(12+10)-\hat{j}(-6-5)+\hat{k}(-4+4) \\ &=22 \hat{i}+11 \hat{j} \\ &=11(2 \hat{i}+\hat{j}) \\ & \therefore|\vec{a} \times \vec{b}|=11 \sqrt{2^{2}+1^{2}}=11 \sqrt{5} \end{aligned} $

इसलिए, समांतर चतुर्भुज का क्षेत्रफल $11 \sqrt{5}$ वर्ग इकाई है।

11. सिद्ध करें कि एक सदिश के दिशा कोसाइन $OX, OY$ और $OZ$ अक्षों के समान झुके हुए हों तो उनके दिशा कोसाइन $\pm(\dfrac{1}{\sqrt{3}}, \dfrac{1}{\sqrt{3}}, \dfrac{1}{\sqrt{3}})$ होते हैं।

उत्तर दिखाएं

हल

मान लीजिए एक सदिश $OX, OY$ और $OZ$ अक्षों के समान कोण $a$ पर झुके हुए है।

तब, सदिश के दिशा कोसाइन $\cos a, \cos a$ और $\cos a$ होते हैं।

अब,

$\cos ^{2} \alpha+\cos ^{2} \alpha+\cos ^{2} \alpha=1$

$\Rightarrow 3 \cos ^{2} \alpha=1$

$\Rightarrow \cos \alpha=\pm \dfrac{1}{\sqrt{3}}$

इसलिए, अक्षों के समान झुके हुए वेक्टर के दिशा कोसाइन $\pm \dfrac{1}{\sqrt{3}}, \pm \dfrac{1}{\sqrt{3}}, \pm \dfrac{1}{\sqrt{3}}$ होते हैं।

12. मान लीजिए $\vec{a}=\hat{i}+4 \hat{j}+2 \hat{k}, \vec{b}=3 \hat{i}-2 \hat{j}+7 \hat{k}$ और $\vec{c}=2 \hat{i}-\hat{j}+4 \hat{k}$. एक सदिश $\vec{d}$ ज्ञात कीजिए जो $\vec{a}$ और $\vec{b}$ दोनों के लंबवत हो और $\vec{c} \cdot \vec{d}=15$ हो।

उत्तर दिखाएं

हल

मान लीजिए $\vec{d}=d_1 \hat{i}+d_2 \hat{j}+d_3 \hat{k}$.

क्योंकि $\vec{d}$ $\vec{a}$ और $\vec{b}$ दोनों के लंबवत है, हमें निम्न प्राप्त होता है:

$\vec{d} \cdot \vec{a}=0$

$\Rightarrow d_1+4 d_2+2 d_3=0$

और,

$\vec{d} \cdot \vec{b}=0$

$\Rightarrow 3 d_1-2 d_2+7 d_3=0$

इसके अतिरिक्त, दिया गया है:

$\vec{c} \cdot \vec{d}=15$

$\Rightarrow 2 d_1-d_2+4 d_3=15$

(1), (2) और (3) को हल करने पर हम प्राप्त करते हैं:

$d_1=\dfrac{160}{3}, d_2=-\dfrac{5}{3}$ और $d_3=-\dfrac{70}{3}$

$\therefore \vec{d}=\dfrac{160}{3} \hat{i}-\dfrac{5}{3} \hat{j}-\dfrac{70}{3} \hat{k}=\dfrac{1}{3}(160 \hat{i}-5 \hat{j}-70 \hat{k})$

इसलिए, अभीष्ट सदिश $\dfrac{1}{3}(160 \hat{i}-5 \hat{j}-70 \hat{k})$ है।

13. सदिश $\hat{i}+\hat{j}+\hat{k}$ के सदिश $2 \hat{i}+4 \hat{j}-5 \hat{k}$ और $\lambda \hat{i}+2 \hat{j}+3 \hat{k}$ के योग के अनुदिश एक एकक सदिश के साथ अदिश गुणनफल एक के बराबर है। $\lambda$ का मान ज्ञात कीजिए।

उत्तर दिखाएं

हल

$(2 \hat{i}+4 \hat{j}-5 \hat{k})+(\lambda \hat{i}+2 \hat{j}+3 \hat{k})$

$=(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}$

इसलिए, सदिश $(2 \hat{i}+4 \hat{j}-5 \hat{k})+(\lambda \hat{i}+2 \hat{j}+3 \hat{k})$ के अनुदिश एकक सदिश निम्नलिखित है:

$\dfrac{(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}}{\sqrt{(2+\lambda)^{2}+6^{2}+(-2)^{2}}}=\dfrac{(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}}{\sqrt{4+4 \lambda+\lambda^{2}+36+4}}=\dfrac{(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}}{\sqrt{\lambda^{2}+4 \lambda+44}}$

सदिश $(\hat{i}+\hat{j}+\hat{k})$ के इस एकक सदिश के साथ अदिश गुणनफल 1 है।

$\Rightarrow(\hat{i}+\hat{j}+\hat{k}) \cdot \dfrac{(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}}{\sqrt{\lambda^{2}+4 \lambda+44}}=1$

$\Rightarrow \dfrac{(2+\lambda)+6-2}{\sqrt{\lambda^{2}+4 \lambda+44}}=1$

$\Rightarrow \sqrt{\lambda^{2}+4 \lambda+44}=\lambda+6$

$\Rightarrow \lambda^{2}+4 \lambda+44=(\lambda+6)^{2}$

$\Rightarrow \lambda^{2}+4 \lambda+44=\lambda^{2}+12 \lambda+36$

$\Rightarrow 8 \lambda=8$

$\Rightarrow \lambda=1$

इसलिए, $\lambda$ का मान 1 है।

14. यदि $\vec{a}, \vec{b}, \overrightarrow{{}c}$ समान परिमाण के परस्पर लम्ब सदिश हैं, तो सिद्ध कीजिए कि सदिश $(\vec{a}+\vec{b}+\vec{c})$ सदिश $\vec{a}, \vec{b}$ और $\vec{c}$ के समान झुकाव रखता है।

उत्तर दिखाएँ

}

हल

चूंकि $\vec{a}, \vec{b}$ और $\vec{c}$ परस्पर लम्ब वेक्टर हैं, हम लिख सकते हैं:

$\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{c}=\vec{c} \cdot \vec{a}=0$.

दिया गया है कि:

$|\vec{a}|=|\vec{b}|=|\vec{c}|$

मान लीजिए वेक्टर $\vec{a}+\vec{b}+\vec{c}$, $\vec{a}, \vec{b}$ और $\vec{c}$ के साथ क्रमशः कोण $\theta_1, \theta_2$ और $\theta_3$ पर झुका हुआ है।

तब, हम लिख सकते हैं:

$$ \begin{aligned} \cos \theta_1 & =\dfrac{(\vec{a}+\vec{b}+\vec{c}) \cdot \vec{a}}{|\vec{a}+\vec{b}+\vec{c}||\vec{a}|}=\dfrac{\vec{a} \cdot \vec{a}+\vec{b} \cdot \vec{a}+\vec{c} \cdot \vec{a}}{|\vec{a}+\vec{b}+\vec{c}||\vec{a}|} \\ & =\dfrac{|\vec{a}|^{2}}{|\vec{a}+\vec{b}+\vec{c}||\vec{a}|} \quad[\vec{b} \cdot \vec{a}=\vec{c} \cdot \vec{a}=0] \\ & =\dfrac{|\vec{a}|}{|\vec{a}+\vec{b}+\vec{c}|} \\ \cos \theta_2 & =\dfrac{(\vec{a}+\vec{b}+\vec{c}) \cdot \vec{b}}{|\vec{a}+\vec{b}+\vec{c}||\vec{b}|}=\dfrac{\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{b}+\vec{c} \cdot \vec{b}}{|\vec{a}+\vec{b}+\vec{c}| \cdot|\vec{b}|} \\ & =\dfrac{|\vec{b}|^{2}}{|\vec{a}+\vec{b}+\vec{c}| \cdot|\vec{b}|} \quad[\vec{a} \cdot \vec{b}=\vec{c} \cdot \vec{b}=0] \\ & =\dfrac{|\vec{a}|}{|\vec{a}+\vec{b}+\vec{c}|} \\ \cos \theta_3 & =\dfrac{(\vec{a}+\vec{b}+\vec{c}) \cdot \vec{c}}{|\vec{a}+\vec{b}+\vec{c}||\vec{c}|}=\dfrac{\vec{a} \cdot \vec{c}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{c}}{|\vec{a}+\vec{b}+\vec{c}||\vec{c}|} \\ & =\dfrac{|\vec{c}|^{2}}{|\vec{a}+\vec{b}+\vec{c}||\vec{c}|} \\ & =\dfrac{|\vec{c}|}{|\vec{a}+\vec{b}+\vec{c}|} \end{aligned} $$

अब, चूंकि $|\vec{a}|=|\vec{b}|=|\vec{c}|, \cos \theta_1=\cos \theta_2=\cos \theta_3$.

$\therefore \theta_1=\theta_2=\theta_3$

अतः, वेक्टर $(\vec{a}+\vec{b}+\vec{c})$, $\vec{a}, \vec{b}$ और $\vec{c}$ के समान कोण पर झुका हुआ है।

15. सिद्ध कीजिए कि $(\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b})=|\vec{a}|^{2}+|\vec{b}|^{2}$, यदि और केवल यदि $\vec{a}, \vec{b}$ लम्ब वेक्टर हैं, दिया गया है कि $\vec{a} \neq \overrightarrow{{}0}, \vec{b} \neq \overrightarrow{{}0}$.

उत्तर दिखाएं

हल

$(\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b})=|\vec{a}|^{2}+|\vec{b}|^{2}$

$\Leftrightarrow \vec{a} \cdot \vec{a}+\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{a}+\vec{b} \cdot \vec{b}=|\vec{a}|^{2}+|\vec{b}|^{2} \quad$ [अद्वितीयता के अंतर्गत अदिश गुणन के योग पर वितरण]

$\Leftrightarrow|\vec{a}|^{2}+2 \vec{a} \cdot \vec{b}+|\vec{b}|^{2}=|\vec{a}|^{2}+|\vec{b}|^{2} \quad[\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}$ (अदिश गुणन संवृत्त होता है)

$\Leftrightarrow 2 \vec{a} \cdot \vec{b}=0$

$\Leftrightarrow \vec{a} \cdot \vec{b}=0$

$\therefore \vec{a}$ और $\vec{b}$ लंबवत हैं। $\quad[\vec{a} \neq \overrightarrow{{}0}, \vec{b} \neq \overrightarrow{{}0}$ (दिया गया) $]$

16 से 19 अभ्यास के लिए सही उत्तर चुनें।

16. यदि $\theta$ दो सदिश $\vec{a}$ और $\vec{b}$ के बीच कोण है, तो $\vec{a} \cdot \vec{b} \geq 0$ केवल जब

(A) $0<\theta<\dfrac{\pi}{2}$

(B) $0 \leq \theta \leq \dfrac{\pi}{2}$

(C) $0<\theta<\pi$

(D) $0 \leq \theta \leq \pi$

उत्तर दिखाएं

हल

मान लीजिए $\theta$ दो सदिश $\vec{a}$ और $\vec{b}$ के बीच कोण है।

तब, बिना कोई नुकता के, $\vec{a}$ और $\vec{b}$ गैर-शून्य सदिश हैं ताकि $|\vec{a}|$ और $|\vec{b}|$ धनात्मक हैं।

यह ज्ञात है कि $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta$।

$\therefore \vec{a} \cdot \vec{b} \geq 0$

$\Rightarrow|\vec{a}||\vec{b}| \cos \theta \geq 0$

$\Rightarrow \cos \theta \geq 0 \quad[|\vec{a}|$ और $|\vec{b}|$ धनात्मक हैं $]$

$\Rightarrow 0 \leq \theta \leq \dfrac{\pi}{2}$

अतः, $\vec{a} \cdot \vec{b} \geq 0$ जब $0 \leq \theta \leq \dfrac{\pi}{2}$ हो।

सही उत्तर है $B$।

17. मान लीजिए $\vec{a}$ और $\vec{b}$ दो एकक सदिश हैं और $\theta$ उनके बीच कोण है। तब $\vec{a}+\vec{b}$ एक एकक सदिश होगा जब

(A) $\theta=\dfrac{\pi}{4}$

(B) $\theta=\dfrac{\pi}{3}$

(C) $\theta=\dfrac{\pi}{2}$

(D) $\theta=\dfrac{2 \pi}{3}$

उत्तर दिखाएं

हल

मान लीजिए $\vec{a}$ और $\vec{b}$ दो एकक सदिश हैं और $\theta$ उनके बीच का कोण है।

तब, $|\vec{a}|=|\vec{b}|=1$ है।

अब, $\vec{a}+\vec{b}$ एक एकक सदिश होगा यदि $|\vec{a}+\vec{b}|=1$ है।

$ \begin{aligned} & |\vec{a}+\vec{b}|=1 \\ & \Rightarrow(\vec{a}+\vec{b})^{2}=1 \\ & \Rightarrow(\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b})=1 \\ & \Rightarrow \vec{a} \cdot \vec{a}+\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{a}+\vec{b} \cdot \vec{b}=1 \\ & \Rightarrow|\vec{a}|^{2}+2 \vec{a} \cdot \vec{b}+|\vec{b}|^{2}=1 \\ & \Rightarrow 1^{2}+2|\vec{a}||\vec{b}| \cos \theta+1^{2}=1 \\ & \Rightarrow 1+2 \cdot 1 \cdot 1 \cos \theta+1=1 \\ & \Rightarrow \cos \theta=-\dfrac{1}{2} \\ & \Rightarrow \theta=\dfrac{2 \pi}{3} \end{aligned} $

अतः, $\vec{a}+\vec{b}$ एक एकक सदिश होगा यदि $\theta=\dfrac{2 \pi}{3}$ है।

सही उत्तर D है।

18. $\hat{i} \cdot(\hat{j} \times \hat{k})+\hat{j} \cdot(\hat{i} \times \hat{k})+\hat{k} \cdot(\hat{i} \times \hat{j})$ का मान है

(A) 0

(B) -1

(C) 1

(D) 3

उत्तर दिखाएं

हल

$ \begin{aligned} & \hat{i} \cdot(\hat{j} \times \hat{k})+\hat{j} \cdot(\hat{i} \times \hat{k})+\hat{k} \cdot(\hat{i} \times \hat{j}) \\ & =\hat{i} \cdot \hat{i}+\hat{j} \cdot(-\hat{j})+\hat{k} \cdot \hat{k} \\ & =1-\hat{j} \cdot \hat{j}+1 \\ & =1-1+1 \\ & =1 \end{aligned} $

सही उत्तर C है।

19. यदि $\theta$ दो सदिशों $\vec{a}$ और $\vec{b}$ के बीच का कोण है, तो $|\vec{a} \cdot \vec{b}|=|\vec{a} \times \vec{b}|$ जब $\theta$ के बराबर है

(A) 0

(B) $\dfrac{\pi}{4}$

(C) $\dfrac{\pi}{2}$

(D) $\pi$

उत्तर दिखाएं

हल

मान लीजिए $\theta$ दो सदिशों $\vec{a}$ और $\vec{b}$ के बीच का कोण है।

तब, बिना कोई अपवाद के, $\vec{a}$ और $\vec{b}$ गैर-शून्य सदिश हैं, इसलिए

$|\vec{a}|$ और $|\vec{b}|$ धनात्मक हैं

$|\vec{a} \cdot \vec{b}|=|\vec{a} \times \vec{b}|$

$\Rightarrow|\vec{a}||\vec{b}| \cos \theta=|\vec{a}||\vec{b}| \sin \theta$

$\Rightarrow \cos \theta=\sin \theta \quad[|\vec{a}|$ और $|\vec{b}|$ धनात्मक है $]$

$\Rightarrow \tan \theta=1$

$\Rightarrow \theta=\dfrac{\pi}{4}$

इसलिए, जब $\theta$ का मान $\dfrac{\pi}{4}$ होता है तब $|\vec{a} \vec{b}|=|\vec{a} \times \vec{b}|$ होता है।

सही उत्तर $B$ है।

सारांश

• बिंदु $P(x, y, z)$ का स्थिति वेक्टर $ \overrightarrow{{}OP}(=\vec{r})=x \hat{i}+y \hat{j}+z \hat{k} $ द्वारा दिया जाता है, और इसके परिमाण $ \sqrt{x^{2}+y^{2}+z^{2}} $ द्वारा दिया जाता है।

• एक वेक्टर के अदिश घटक इसके दिशा अनुपात होते हैं, और इनका अर्थ अक्षों के अनुदिश प्रक्षेप होते हैं।

• किसी भी सदिश के परिमाण $(r)$, दिशा अनुपात $(a, b, c)$ और दिशा कोसाइन $(l, m, n)$ के बीच संबंध निम्नलिखित है:

$ \qquad l=\dfrac{a}{r}, \quad m=\dfrac{b}{r}, \quad n=\dfrac{c}{r} $

• एक त्रिभुज के तीन भुजाओं के सदिश योगफल, जो क्रम में लिए गए हैं, $\overrightarrow{{}0}$ होता है।

• दो सदिशों के सदिश योगफल को उन दो सदिशों के आसन्न भुजाओं वाले समांतर चतुर्भुज के विकर्ण द्वारा दिया जाता है।

• एक दिए गए सदिश को एक अदिश $\lambda$ से गुणा करने पर, सदिश के परिमाण को $|\lambda|$ गुना बदल देता है, और दिशा अपरिवर्तित रहती है (या विपरीत दिशा बन जाती है), जितना कि $\lambda$ का मान धनात्मक (या नकारात्मक) होता है।

• एक दिए गए सदिश $\vec{a}$ के लिए, सदिश $\hat{a}=\dfrac{\vec{a}}{|\vec{a}|}$ दिशा $\vec{a}$ के अनुदिश एक एकक सदिश देता है।

• बिंदु $P$ और $Q$ के स्थिति सदिश क्रमशः $\vec{a}$ और $\vec{b}$ हैं, जो बिंदु $R$ के बीच रेखा खंड को $m:n$ के अनुपात में विभाजित करता है, तो: (i) आंतरिक विभाजन के लिए, बिंदु $R$ के स्थिति सदिश को $\dfrac{n \vec{a}+m \vec{b}}{m+n}$ द्वारा दिया जाता है। (ii) बाह्य विभाजन के लिए, बिंदु $R$ के स्थिति सदिश को $\dfrac{m \vec{b}-n \vec{a}}{m-n}$ द्वारा दिया जाता है।

• दो दिए गए सदिश $\vec{a}$ और $\vec{b}$ के बीच कोण $\theta$ के बीच अदिश गुणनफल निम्नलिखित है:

$ \qquad \vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta $

$\qquad$ अतः, जब $\vec{a} \cdot \vec{b}$ दिया गया हो, तो दो सदिशों $\vec{a}$ और $\vec{b}$ के बीच कोण ’ $\theta$ ’ को निम्नलिखित द्वारा निर्धारित किया जा सकता है:

$ \qquad \cos \theta=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} $

• यदि $\theta$ दो सदिश $\vec{a}$ और $\vec{b}$ के बीच कोण हो, तो उनका क्रॉस गुणनफल निम्नलिखित है:

$ \qquad \vec{a} \times \vec{b}=|\vec{a} | \vec{b}| \sin \theta \hat{n} $

$\qquad$ जहाँ $\hat{n}$ एक एकक सदिश है जो $\vec{a}$ और $\vec{b}$ के बर्ताव करने वाले तल के लंबवत है। ऐसा कि $\vec{a}, \vec{b}, \hat{n}$ एक दाएं हाथ के निर्देश अक्षों के तंत्र को बनाते हैं।

• यदि हम दो सदिश $\vec{a}$ और $\vec{b}$ को घटक रूप में दिया गया है, जहाँ $\vec{a}=a _ {1} \hat{i}+a _ {2} \hat{j}+a _ {3} \hat{k}$ और $\vec{b}=b _ {1} \hat{i}+b _ {2} \hat{j}+b _ {3} \hat{k}$ और $\lambda$ कोई अदिश है,

$\qquad$ फिर $\vec{a}+\vec{b} =(a _ {1}+b _ {1}) \hat{i}+(a _ {2}+b _ {2}) \hat{j}+(a _ {3}+b _ {3}) \hat{k}$

$\qquad \lambda \vec{a} =(\lambda a _ {1}) \hat{i}+(\lambda a _ {2}) \hat{j}+(\lambda a _ {3}) \hat{k}$

$\qquad \vec{a} \cdot \vec{b} =a _ {1} b _ {1}+a _ {2} b _ {2}+a _ {3} b _ {3}$

$ \qquad\text{ और } \quad \vec{a} \times \vec{b}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{vmatrix} \text{. } $

ऐतिहासिक टिप्पणी

“वेक्टर” शब्द का उत्पत्ति लैटिन शब्द vectus से हुई है, जिसका अर्थ “ले जाना” होता है। आधुनिक वेक्टर सिद्धांत के मूल विचार लगभग 1800 के आसपास थे जब कैस्पर वेसेल (1745-1818) और जैन रोबर्ट अर्गंड (1768-1822) ने बताया कि एक सम复数 $a+i b$ को एक समन्वय तल में एक दिशात्मक रेखा खंड की सहायता से एक ज्यामितीय व्याख्या दी जा सकती है। विलियम रोवेन हैमिल्टन (1805-1865), एक आयरिश गणितज्ञ, ने अपनी किताब Lectures on Quaternions (1853) में एक दिशात्मक रेखा खंड के लिए “वेक्टर” शब्द का प्रयोग पहले किया। हैमिल्टन के क्वाटर्नियन के विधि (एक चार वास्तविक संख्याओं के क्रमित समुच्चय के रूप में दिया गया है: $a+b \hat{i}+c \hat{j}+d \hat{k}, \hat{i}, \hat{j}, \hat{k}$ निश्चित बीजगणितीय नियमों के अनुसार) तीन आयामी अंतर के वेक्टर के गुणन की समस्या के समाधान बन गई। हालांकि, यहां ध्यान देना आवश्यक है कि वेक्टर की अवधारणा और उनके जोड़ के बारे में विचार बहुत पहले से ही जाने जा रहे थे, जब से अरस्तू (384-322 ई.पू.), एक ग्रीक दार्शनिक, और प्लेटो (427-348 ई.पू.) के शिष्य थे। उस समय यह माना जाता था कि दो या अधिक बलों के संयोजन के प्रभाव को समानांतर चतुर्भुज के नियम के अनुसार जोड़कर देखा जा सकता है। बलों के संयोजन के सही नियम, जिसमें बल वेक्टरीय रूप से जोड़े जाते हैं, के लिए लेटिन-सिमन स्टीविन (1548-1620) ने लंब बलों के मामले में खोज कर दिया। 1586 ई. में, उन्होंने अपने ग्रंथ DeBeghinselen der Weeghconst (“वेटिंग कला के सिद्धांत”) में बलों के ज्यामितीय जोड़ के सिद्धांत का विश्लेषण किया, जिसने बलों के विकास में एक महत्वपूर्ण उछाल लाया। लेकिन वेक्टर के सामान्य अवधारणा के गठन में इसके लिए एक और 200 वर्ष लग गए।

1880 में, अमेरिकी भौतिकज्ञ और गणितज्ञ जोसेफ विलार्ड गिब्स (1839-1903) और ब्रिटिश इंजीनियर ओलिवर हेविसाइड (1850-1925) ने अब हम इसे वेक्टर विश्लेषण के रूप में जानते हैं, के विकास में योगदान दिया। इसे मुख्य रूप से जॉर्डन के वास्तविक (स्केलर) भाग को अपने काल्पनिक (वेक्टर) भाग से अलग करके किया गया। 1881 और 1884 में, गिब्स ने एक ग्रंथ वेक्टर विश्लेषण के तत्व के नाम से प्रकाशित किया। इस किताब ने वेक्टर के व्यवस्थित और संक्षिप्त विवरण प्रस्तुत किया। हालांकि, वेक्टर के अनुप्रयोगों के दर्शन के लिए अधिकांश श्रेय ओलिवर हेविसाइड और पी.जी. टैट (1831-1901) को जाता है, जिन्होंने इस विषय में महत्वपूर्ण योगदान दिया।