अध्याय 12 सीमा और अवकलज
कलन के रूप में कुंजी के साथ, गणित के अनुप्रयोग के सफल व्याख्या के लिए प्रकृति के प्रवाह की व्याख्या की जा सकती है - व्हाइटहेड
12.1 परिचय
इस अध्याय कलन का परिचय है। कलन वह गणित की शाखा है जो मुख्य रूप से फलन के मान के परिवर्तन के अध्ययन के साथ संबंधित है जब डोमेन में बिंदुओं के परिवर्तन होते हैं। पहले, हम अवकलज के एक अनुमानित विचार (वास्तव में अवकलज की परिभाषा किए बिना) देते हैं। फिर हम एक असंवेदनशील परिभाषा देते हैं और सीमा के कुछ बीजगणित के अध्ययन करते हैं। फिर हम अवकलज की परिभाषा पर वापस आते हैं और अवकलज के कुछ बीजगणित के अध्ययन करते हैं। हम अपने अवकलज के कुछ मानक फलनों के अवकलज भी प्राप्त करते हैं।

सर आइज़ैक न्यूटन (1642-1727 ई.स. )
12.2 अवकलज के अनुभूति आधारित अवधारणा
भौतिक प्रयोगों ने पुष्टि किया है कि एक वस्तु जो एक ऊँचे किनारे से गिरती है, $t$ सेकंड में $4.9 t^{2}$ मीटर की दूरी तय करती है, अर्थात वस्तु द्वारा $t$ सेकंड में तय की गई दूरी $s$ मीटर में निम्नलिखित द्वारा दी जाती है $s=4.9 t^{2}$.
दी गई तालिका 13.1 एक ऊँची खंड में गिरते शरीर के विभिन्न समय अंतरालों में तय की गई दूरी (मीटर में) दिखाती है।
उद्देश्य यह ज्ञात करना है कि शरीर की गति $t=2$ सेकंड पर कितनी है। इस समस्या के लिए एक तरीका विभिन्न समय अंतरालों के औसत वेग की गणना करके और उम्मीद करके कि ये $t=2$ सेकंड पर गति के बारे में कुछ जानकारी प्रदान करेंगे।
समय $t=t_1$ और $t=t_2$ के बीच औसत वेग $t=t_1$ और $t=t_2$ के बीच तय की गई दूरी को $(t_2 - t_1)$ से विभाजित करके प्राप्त किया जाता है। इसलिए, पहले दो सेकंड के औसत वेग:
$ \begin{aligned} & =\dfrac{\text{ Distance travelled between } t_2=2 \text{ and } t_1=0}{\text{ Time interval }(t_2-t_1)} \\ & =\dfrac{(19.6-0) m}{(2-0) s}=9.8 m / s . \end{aligned} $
उसी तरह, $t=1$ और $t=2$ के बीच औसत वेग है
$ \dfrac{(19.6-4.9) m}{(2-1) s}=14.7 m / s $
इसी तरह हम $t=t_1$ और $t=2$ के बीच औसत वेग की गणना करते हैं जहाँ $t_1$ के विभिन्न मान होते हैं। नीचे दिए गए तालिका 13.2 में औसत वेग $(v)$, $t=t_1$ सेकंड और $t=2$ सेकंड के लिए दिया गया है।
तालिका 12.1
$ \begin{array}{|c|c|}
\hline t & s \\ \hline 0 & 0 \\ \hline 1 & 4.9 \\ \hline 1.5 & 11.025 \\ \hline 1.8 & 15.876 \\ \hline 1.9 & 17.689 \\ \hline 1.95 & 18.63225 \\ \hline 2 & 19.6 \\ \hline 2.05 & 20.59225 \\ \hline 2.1 & 21.609 \\ \hline 2.2 & 23.716 \\ \hline 2.5 & 30.625 \\ \hline 3 & 44.1 \\ \hline 4 & 78.4 \\ \hline \end{array} $
तालिका 12.2
$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline t_1 & 0 & 1 & 1.5 & 1.8 & 1.9 & 1.95 & 1.99 \\ \hline v & 9.8 & 14.7 & 17.15 & 18.62 & 19.11 & 19.355 & 19.551 \\
\hline \end{array} $
तालिका 12.2 से हम देखते हैं कि औसत वेग धीरे-धीरे बढ़ रहा है। जैसे हम $t=2$ पर समाप्त होने वाले समय अंतराल को छोटा करते जाते हैं, हम देखते हैं कि हम $t=2$ पर वेग के बारे में बेहतर अनुमान लगा सकते हैं। 1.99 सेकंड और 2 सेकंड के बीच कुछ बड़ा घटना न होने की उम्मीद करते हुए, हम निष्कर्ष निकालते हैं कि $t=2$ सेकंड पर औसत वेग ठीक $19.551 मी / से के ऊपर है।
इस निष्कर्ष को निम्नलिखित संगणना के सेट द्वारा कुछ अधिक मजबूत बनाया जा सकता है। $t=2$ सेकंड पर शुरू होने वाले विभिन्न समय अंतराल के लिए औसत वेग की गणना करें। जैसा कि पहले था, $t=2$ सेकंड और $t=t_2$ सेकंड के बीच औसत वेग $v$ है:
$ \begin{aligned} & =\dfrac{\text{ 2 सेकंड और } t_2 \text{ सेकंड के बीच तय की गई दूरी }}{t_2-2} \\ & =\dfrac{\text{ } t_2 \text{ सेकंड में तय की गई दूरी }- \text{ 2 सेकंड में तय की गई दूरी }}{t _2-2} \end{aligned} $
$ =\dfrac{\text{ } t_2 \text{ सेकंड में तय की गई दूरी }-19.6}{t_2-2} $
नीचे दिए गए तालिका 12.3 में $v$ के औसत वेग मीटर प्रति सेकंड के बीच $t=2$ सेकंड और $t_2$ सेकंड के बीच दिया गया है।
तालिका 12.3
$ \begin{array}{|c|c|c|c|c|c|c|c|}
\hline t_2 & 4 & 3 & 2.5 & 2.2 & 2.1 & 2.05 & 2.01 \\ \hline v & 29.4 & 24.5 & 22.05 & 20.58 & 20.09 & 19.845 & 19.649 \\ \hline \end{array} $
यहाँ फिर से हम ध्यान देते हैं कि यदि हम $t=2$ से शुरू होने वाले छोटे समय अंतराल लें, तो हमें $t=2$ पर वेग के बारे में बेहतर अनुमान लेने में मदद मिलती है।
पहले सेट के गणना में, हमने $t=2$ पर समाप्त होने वाले बढ़ते समय अंतराल में औसत वेग निकाले और फिर यह अनुमान लगाया कि $t=2$ के ठीक पहले कुछ बड़ी घटना नहीं होती। दूसरे सेट के गणना में, हमने $t=2$ पर समाप्त होने वाले घटते समय अंतराल में औसत वेग निकाले और फिर यह अनुमान लगाया कि $t=2$ के ठीक बाद कुछ बड़ी घटना नहीं होती। भौतिक आधार पर, इन दोनों औसत वेग के अनुक्रम एक सामान्य सीमा के निकट जाने चाहिए। हम यह सुरक्षित तौर पर निष्कर्ष ले सकते हैं कि $t=2$ पर वस्तु का वेग $19.551 मी/से और 19.649 मी/से के बीच है। तकनीकी रूप से, हम कहते हैं कि $t=2$ पर क्षणिक वेग $19.551 मी/से और 19.649 मी/से के बीच है। जैसा कि ज्ञात है, वेग विस्थापन के परिवर्तन की दर होती है। इसलिए जो हमने किया है वह निम्नलिखित है। विभिन्न समय के बिंदुओं पर तय की गई दूरी के डेटा के आधार पर हमने एक निश्चित समय के बिंदु पर दूरी के परिवर्तन की दर का अनुमान लगाया है। हम कहते हैं कि दूरी फलन $s=4.9 t^{2}$ के अवकलज $t=2$ पर 19.551 और 19.649 के बीच है।
एक अलग तरीका इस सीमा प्रक्रिया को देखने के लिए चित्र 12.1 में दिखाया गया है। यह एक ग्राफ है जिसमें शरीर की चट्टान के शीर्ष से दूरी $s$ और घटने वाले समय $t$ के बीच एक संबंध है। जब समय अंतराल के अनुक्रम $h_1, h_2, \ldots$ शून्य के निकट आते हैं, तो औसत वेग के अनुक्रम की सीमा उतनी ही अधिक होती है जितनी कि अनुपात के अनुक्रम की सीमा होती है।

चित्र 12.1
$ \dfrac{C_1 B_1}{AC_1}, \dfrac{C_2 B_2}{AC_2}, \dfrac{C_3 B_3}{AC_3}, \ldots $
$ \begin{aligned} \lim\limits_{x \to 0} f(x)=0 \end{aligned} $
(to be read as limit of $f(x)$ as $x$ tends to zero equals zero). The limit of $f(x)$ as $x$ tends to zero is to be thought of as the value $f(x)$ should assume at $x=0$.
In general as $x \to a, f(x) \to l$, then $l$ is called limit of the function $f(x)$ which is symbolically written as $\lim\limits_{x \to a} f(x)=l$.
Consider the following function $g(x)=|x|, x \neq 0$. Observe that $g(0)$ is not defined. Computing the value of $g(x)$ for values of $x$ very near to 0 , we see that the value of $g(x)$ moves towards 0 . So, $\lim\limits_{x \to 0} g(x)=0$. This is intuitively clear from the graph of $y=|x|$ for $x \neq 0$. (See Fig 2.13, Chapter 2).
Consider the following function.
$ h(x)=\dfrac{x^{2}-4}{x-2}, x \neq 2 $
Compute the value of $h(x)$ for values of $x$ very near to 2 (but not at 2 ). Convince yourself that all these values are near to 4 . This is somewhat strengthened by considering the graph of the function $y=h(x)$ given here (Fig 12.2).

चित्र 12.2
इन सभी चित्रों में फलन के एक दिए गए बिंदु $x=a$ पर मान किस तरह $x$ $a$ के निकट आ रहा है इस पर निर्भर नहीं करता। ध्यान दें कि $x$ एक संख्या $a$ के निकट कैसे पहुंच सकता है इसके दो मुख्य तरीके हो सकते हैं, या तो बाईं ओर या दाईं ओर, अर्थात सभी $x$ के मान $a$ के निकट बराबर या उससे कम हो सकते हैं या उससे अधिक हो सकते हैं। इस प्रकार दो अलग-अलग सीमाएं आती हैं - दाईं ओर सीमा और बाईं ओर सीमा. एक फलन $f(x)$ की दाईं ओर सीमा वह मान होती है जो $x$ $a$ के दाईं ओर निकट आ रहा है उस समय $f(x)$ के मानों द्वारा निर्धारित होती है। इसी तरह, बाईं ओर सीमा. इसकी व्याख्या के लिए, एक फलन लें
$ f(x)= \begin{cases}1, & x \leq 0 \\ 2, & x>0\end{cases} $
इस फलन का ग्राफ चित्र 12.3 में दिखाया गया है। स्पष्ट है कि 0 पर $f$ का मान $x \leq 0$ के लिए $f(x)$ के मानों द्वारा निर्धारित होता है जो 1 के बराबर है, अर्थात, $f(x)$ का 0 पर बाई ओर सीमा है
$ \lim\limits_{x \to 0} f(x)=1 . $

चित्र 12.3
उसी तरह, $x>0$ के लिए $f(x)$ के मानों द्वारा 0 पर $f$ का मान 2 के बराबर होता है, अर्थात, $f(x)$ का 0 पर दाई ओर सीमा है
$ \lim\limits_{x \to 0^{+}} f(x)=2. $
इस मामले में दाहिना और बाईं ओर की सीमा अलग-अलग होती है, और इसलिए हम कहते हैं कि $f(x)$ की सीमा $x$ शून्य के निकट आते हैं तो नहीं मौजूद है (हालांकि फलन 0 पर परिभाषित है)।
सारांश
हम कहते हैं कि $\lim\limits_{x \to a^{-}} f(x)$, $x=a$ पर $f$ का अपेक्षित मान है, जो $a$ के बाईं ओर $x$ के पास $f$ के मानों के आधार पर दिया गया है। इस मान को $a$ पर $f$ की बाईं ओर की सीमा कहते हैं।
हम कहते हैं कि $\lim\limits_{x \to a^{+}} f(x)$, $x=a$ पर $f$ का अपेक्षित मान है, जो $a$ के दाहिने ओर $x$ के पास $f$ के मानों के आधार पर दिया गया है। इस मान को $a$ पर $f(x)$ की दाहिनी ओर की सीमा कहते हैं।
अगर दाहिना और बाईं ओर के सीमाएँ मेल खाती हैं, तो हम उस सामान्य मान को $f(x)$ के $x=a$ पर सीमा कहते हैं और इसे $\lim\limits_{x \to a} f(x)$ द्वारा दर्शाते हैं।
उदाहरण 1 मान लीजिए कि फलन $f(x)=x+10$ है। हम इस फलन के $x=5$ पर सीमा ज्ञात करना चाहते हैं। चलो हम $x$ के 5 के बहुत करीब के मानों पर फलन $f(x)$ के मान की गणना करें। 5 के बाईं ओर और निकट वाले कुछ बिंदु $4.9, 4.95, 4.99, 4.995 \ldots$ आदि हैं। इन बिंदुओं पर फलन के मान नीचे तालिका के रूप में दिए गए हैं। इसी तरह, वास्तविक संख्या 5.001,
5.01, 5.1 भी 5 के निकट और दाहिने ओर के बिंदु हैं। इन बिंदुओं पर फलन के मान तालिका 12.4 में दिए गए हैं।
तालिका 12.4
$ \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline x & 4.9 & 4.95 & 4.99 & 4.995 & 5.001 & 5.01 & 5.1 \\ \hline f(x) & 14.9 & 14.95 & 14.99 & 14.995 & 15.001 & 15.01 & 15.1 \\ \hline \end{array} $
तालिका 12.4 से हम निष्कर्ष निकाल सकते हैं कि $x=5$ पर $f(x)$ का मान 14.995 से अधिक और 15.001 से कम होना चाहिए, यह मान लें कि $x=4.995$ और 5.001 के बीच कुछ असामान्य घटना नहीं होती। यह उचित मान लेना है कि $x=5$ पर $f(x)$ का मान, 5 के बाईं ओर के संख्याओं के आधार पर 15 होता है, अर्थात,
$ \lim\limits_{x \to 5^{-}} f(x)=15. $
इसी तरह, जब $x$ 5 के दाहिने ओर से प्राप्त होता है, $f(x)$ का मान 15 होना चाहिए, अर्थात,
$ \lim\limits_{x \to 5^{+}} f(x)=15. $
इसलिए, संभवतः $f(x)$ के बाईं ओर की सीमा और दाईं ओर की सीमा दोनों 15 के बराबर होंगी। इसलिए,
$ \lim\limits_{x \to 5^{-}} f(x)=\lim\limits_{x \to 5^{+}} f(x)=\lim\limits_{x \to 5} f(x)=15 . $
इस फलन के ग्राफ को देखकर इस निष्कर्ष को थोड़ा मजबूत बनाया जा सकता है, जो अध्याय 2 के आकृति 2.16 में दिया गया है। इस आकृति में हम देखते हैं कि जब $x$ कोई भी दिशा से 5 के निकट आता है, तो फलन $f(x)=x+10$ के ग्राफ बिंदु $(5,15)$ के निकट आता है।
हम देखते हैं कि $x=5$ पर फलन का मान भी 15 के बराबर होता है।
उदाहरण 2 फलन $f(x)=x^{3}$ को लेते हैं। हम इस फलन के $x=1$ पर सीमा ज्ञात करने की कोशिश करते हैं। पिछले मामले की तरह चलते हुए, हम $x$ के 1 के पास के मानों पर $f(x)$ के मान को सारणीबद्ध करते हैं। यह तालिका 12.5 में दी गई है।
तालिका 12.5
$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline x & 0.9 & 0.99 & 0.999 & 1.001 & 1.01 & 1.1 \\ \hline f(x) & 0.729 & 0.970299 & 0.997002999 & 1.003003001 & 1.030301 & 1.331 \\
\hline \end{array} $
इस तालिका से हम निष्कर्ष निकाल सकते हैं कि $f(x)$ का मान $x=1$ पर 0.997002999 से अधिक और 1.003003001 से कम होना चाहिए, यह मान लें कि $x=0.999$ और 1.001 के बीच कोई धमाकेदार घटना नहीं होती। यह तर्कसंगत है कि $x=1$ पर $f(x)$ का मान, 1 के बाईं ओर के संख्याओं के आधार पर 1 होता है, अर्थात,
$ \lim\limits_{x \to 1^{-}} f(x)=1 \text{. } $
उसी तरह, जब $x$ 1 के दाईं ओर से पहुंचता है, $f(x)$ का मान 1 होता है, अर्थात,
$ \lim\limits_{x \to 1^{+}} f(x)=1 \text{. } $
$
अतः, $f(x)$ के बाईं ओर सीमा और $f(x)$ के दाईं ओर सीमा दोनों 1 के बराबर हो सकती हैं। इसलिए,
$ \lim\limits_{x \to 1^{-}} f(x)=\lim\limits_{x \to 1^{+}} f(x)=\lim\limits_{x \to 1} f(x)=1 . $
इस फलन के ग्राफ को देखकर इस निष्कर्ष को कुछ अधिक मजबूत बनाया जा सकता है, जो अध्याय 2 में आकृति 2.11 में दिया गया है। इस आकृति में हम देखते हैं कि जब $x$ कोई भी दिशा से 1 के निकट आता है, तो फलन $f(x)=x^{3}$ के ग्राफ बिंदु $(1,1)$ के निकट आता है।
हम देखते हैं, फिर से, कि $x=1$ पर फलन का मान भी 1 के बराबर होता है।
उदाहरण 3 मान लीजिए कि फलन $f(x)=3 x$ है। हम इस फलन के $x=2$ पर सीमा ज्ञात करने की कोशिश करते हैं। अब नीचे दिया गया तालिका 12.6 स्वयं स्पष्ट हो जाएगी।
तालिका 12.6
$ \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline x & 1.9 & 1.95 & 1.99 & 1.999 & 2.001 & 2.01 & 2.1 \\ \hline f(x) & 5.7 & 5.85 & 5.97 & 5.997 & 6.003 & 6.03 & 6.3 \\ \hline \end{array} $
जैसा कि पहले देखा गया है, हम देखते हैं कि $x$ के 2 से दोनों तरफ से अग्रसर होने पर $f(x)$ का मान 6 के निकट लगता है। हम इसे इस प्रकार रिकॉर्ड करते हैं:
$ \lim\limits_{x \to 2^{-}} f(x)=\lim\limits_{x \to 2^{+}} f(x)=\lim\limits_{x \to 2} f(x)=6 $
आकृति 12.4 में दिखाए गए ग्राफ इस तथ्य को मजबूत करता है।

आकृति 13.4
यहाँ फिर से हम ध्यान देते हैं कि $x=2$ पर फलन का मान $x=2$ पर सीमा के साथ मेल खाता है।
उदाहरण 4 मान लीजिए स्थिर फलन $f(x)=3$ है। हम इसकी सीमा $x=2$ पर खोजने की कोशिश करते हैं। यह फलन स्थिर फलन होने के कारण हमेशा एक ही मान (इस मामले में 3) ले लेता है, अर्थात इसके मान $x=2$ के पास के बिंदुओं पर 3 होता है। अतः
$ \lim\limits_{x \to 2} f(x)=\lim\limits_{x \to 2^{+}} f(x)=\lim\limits_{x \to 2} f(x)=3 $
$ f(x)=3 $ के ग्राफ कोई भी $ x $-अक्ष के समानांतर रेखा है जो $ (0,3) $ से गुजरती है और चित्र 2.9 में दिखाया गया है, अध्याय 2 में। इससे भी स्पष्ट है कि आवश्यक सीमा 3 है। वास्तव में, यह आसानी से देखा जा सकता है कि किसी भी वास्तविक संख्या $ a $ के लिए $ \lim\limits_{x \to a} f(x)=3 $ है।
उदाहरण 5 मान लीजिए कि फलन $ f(x)=x^{2}+x $ है। हम $ \lim\limits_{x \to 1} f(x) $ ज्ञात करना चाहते हैं। हम $ x=1 $ के पास $ f(x) $ के मानों को तालिका 12.7 में सारांशित करते हैं।
तालिका 12.7
$ \begin{array}{|c|c|c|c|c|c|c|} \hline x & 0.9 & 0.99 & 0.999 & 1.01 & 1.1 & 1.2 \\ \hline f(x) & 1.71 & 1.9701 & 1.997001 & 2.0301 & 2.31 & 2.64 \\ \hline \end{array} $
इससे यह तर्क देने के लिए उचित है कि $\lim\limits_{x \to 1^{-}} f(x)=\lim\limits_{x \to 1^{+}} f(x)=\lim\limits_{x \to 1} f(x)=2$।
चित्र 12.5 में दिखाए गए $f(x)=x^{2}+x$ के ग्राफ से स्पष्ट है कि जब $x$ 1 के निकट आता है, तो ग्राफ $(1,2)$ के निकट आता है।

यहाँ, फिर से हम देखते हैं कि
$ \lim\limits_{x \to 1} f(x)=f(1) $
अब, निम्नलिखित तीन तथ्यों को स्वयं विश्वास कर लें:
$ \qquad \qquad \qquad \lim\limits_{x \to 1} x^{2}=1, \lim\limits_{x \to 1} x=1 \text{ और } \lim\limits_{x \to 1} x+1=2 $
तब $ \quad\quad\quad\quad \lim\limits_{x \to 1} x^{2}+\lim\limits_{x \to 1} x=1+1=2=\lim\limits_{x \to 1}[x^{2}+x] \text{। } $
इसके अलावा $ \quad\quad\quad\quad\lim\limits_{x \to 1} x . \lim\limits_{x \to 1}(x+1)=1 \cdot 2=2=\lim\limits_{x \to 1}[x(x+1)]=\lim\limits_{x \to 1}[x^{2}+x] .
$
आकृति 6 फलन $f(x)=\sin x$ को लें। हम $ \lim\limits_{x \to \dfrac{\pi}{2}} \sin x $ के बारे में रुचि रखते हैं, जहाँ कोण रेडियन में मापा जाता है।
यहाँ, हम $\dfrac{\pi}{2}$ के पास $f(x)$ के (लगभग) मान को सारणीबद्ध करते हैं (सारणी 12.8)। इसके आधार पर, हम निष्कर्ष निकाल सकते हैं कि
$ \lim\limits_{x \to \dfrac{\pi^{-}}{2}} f(x)=\lim\limits_{x \to \dfrac{\pi^{+}}{2}} f(x)=\lim\limits_{x \to \dfrac{\pi}{2}} f(x)=1 $
इसके अतिरिक्त, यह फलन $f(x)=\sin x$ के ग्राफ द्वारा समर्थित है, जो चैप्टर 3 के आकृति 3.8 में दिया गया है। इस मामले में भी, हम देखते हैं कि $\lim\limits_{x \to \dfrac{\pi}{2}} \sin x=1$।
तालिका 12.8
$ \begin{array}{|c|c|c|c|c|} \hline x & \frac{\pi}{2}-0.1 & \frac{\pi}{2}-0.01 & \frac{\pi}{2}+0.01 & \frac{\pi}{2}+0.1 \\ \hline f(x) & 0.9950 & 0.9999 & 0.9999 & 0.9950 \\ \hline \end{array} $
उदाहरण 7 फलन $f(x)=x+\cos x$ को लें। हम $x \to 0$ के अग्रिम लिमिट $\lim\limits_{x \to 0} f(x)$ खोजना चाहते हैं। यहाँ हम 0 के पास $f(x)$ के (अनुमानित) मान को सारणीबद्ध कर रहे हैं (तालिका 12.9)।
तालिका 12.9
$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline x & -0.1 & -0.01 & -0.001 & 0.001 & 0.01 & 0.1 \\ \hline \end{array} $
\hline f(x) & 0.9850 & 0.98995 & 0.9989995 & 1.0009995 & 1.00995 & 1.0950 \\ \hline \end{array} $
तालिका 12.9 से हम निष्कर्ष निकाल सकते हैं कि
$ \lim\limits_{x \to 0^{-}} f(x)=\lim\limits_{x \to 0^{+}} f(x)=\lim\limits_{x \to 0} f(x)=1 $
इस मामले में भी हम देखते हैं कि $\lim\limits_{x \to 0} f(x)=f(0)=1$।
अब, आप खुद को यह सिद्ध करने में सक्षम हो सकते हैं कि
$ \lim\limits_{x \to 0}[x+\cos x]=\lim\limits_{x \to 0} x+\lim\limits_{x \to 0} \cos x \text{ वास्तव में सही है? } $
उदाहरण 8 मान लीजिए कि फलन $f(x)=\dfrac{1}{x^{2}}$ जब $x>0$ हो। हम जानना चाहते हैं $\lim\limits_{x \to 0} f(x)$।
यहाँ ध्यान दें कि फलन के डोमेन को सभी धनात्मक वास्तविक संख्याएँ दी गई है। इसलिए, जब हम $f(x)$ के मानों की सारणी बना रहे हैं, तो $x$ के बाईं ओर 0 के निकट आने के बारे में बात करना अर्थहीन हो जाता है। नीचे हम ऐसे धनात्मक $x$ के मानों के लिए फलन के मानों की सारणी बना रहे हैं (इस सारणी में $n$ कोई भी धनात्मक पूर्णांक निरूपित करता है)।
नीचे दी गई सारणी 12.10 से हम देख सकते हैं कि जब $x$ 0 के निकट आता है, तो $f(x)$ बड़ा और बड़ा होता जाता है। यहाँ हम तात्पर्य रखते हैं कि $f(x)$ का मान किसी भी दिए गए संख्या से बड़ा बनाया जा सकता है।
तालिका 12.10
$ \begin{array}{|c|c|c|c|c|} \hline x & 1 & 0.1 & 0.01 & 10^{-n} \\ \hline f(x) & 1 & 100 & 10000 & 10^{2n} \\ \hline \end{array} $
गणितीय रूप से हम कहते हैं
$ \lim\limits_{x \to 0} f(x)=+\infty $
हम यह भी ध्यान रखते हैं कि इस कोर्स में ऐसे सीमा के मामले हम नहीं आएंगे।
उदाहरण 9 हम $ \lim\limits_{x \to 0} f(x) $ ज्ञात करना चाहते हैं, जहाँ
$ f(x)= \begin{cases}x-2, & x<0 \\ 0, & x=0 \\ x+2, & x>0\end{cases} $
सामान्य तौर पर हम $ x $ के 0 के पास के मानों के साथ $ f(x) $ की एक तालिका बनाते हैं। ध्यान दें कि ऋणात्मक मानों के लिए हम $ x-2 $ का मूल्यांकन करना होगा और धनात्मक मानों के लिए हम $ x+2 $ का मूल्यांकन करना होगा।
तालिका 12.11
$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline x & -0.1 & -0.01 & -0.001 & 0.001 & 0.01 & 0.1 \\ \hline f(x) & -2.1 & -2.01 & -2.001 & 2.001 & 2.01 & 2.1 \\ \hline \end{array} $
तालिका 12.11 के पहले तीन प्रविष्टियों से हम निष्कर्ष निकालते हैं कि फलन का मान -2 में घट रहा है और इसलिए।
$ \lim\limits_{x \to 0^{-}} f(x)=-2 $
तालिका के अंतिम तीन प्रविष्टियों से हम निष्कर्ष निकालते हैं कि फलन का मान 2 से बढ़ रहा है और इसलिए
$ \lim\limits_{x \to 0^{+}} f(x)=2
$
क्योंकि 0 पर बाई ओर और दाई ओर सीमा एक ही नहीं है, हम कहते हैं कि फलन के 0 पर सीमा में अस्तित्व नहीं है।
इस फलन के ग्राफ को आकृति 12.6 में दिखाया गया है। यहाँ हम ध्यान देते हैं कि $x=0$ पर फलन का मान सुच्छ रूप से परिभाषित है और वास्तव में 0 के बराबर है, लेकिन $x=0$ पर फलन की सीमा तक निर्धारित नहीं है।

चित्र 12.6
उदाहरण 10 अंतिम उदाहरण के रूप में, हम $\lim\limits_{x \to 1} f(x)$ खोजते हैं,
जहाँ
$ f(x)=\begin{cases} x+2 & x \neq 1 \\ 0 & x=1 \end{cases} $
तालिका 12.12
$ \begin{array}{|c|c|c|c|c|c|c|} \hline x & 0.9 & 0.99 & 0.999 & 1.001 & 1.01 & 1.1 \\ \hline f(x) & 2.9 & 2.99 & 2.999 & 3.001 & 3.01 & 3.1 \\ \hline \end{array} $
सामान्य तौर पर हम $x$ के निकट 1 के मानों के लिए $f(x)$ के मान तैयार करते हैं। $x$ के मानों के लिए $f(x)$ के मान से लगता है कि फलन $x=1$ पर मान 3 ले लेगा, अर्थात,
$ \lim\limits_{x \to 1^{-}} f(x)=3 . $
उसी तरह, $f(x)$ का मान $x$ के मानों के आधार पर 1 से बड़े मानों पर दिए गए मान के अनुसार 3 होना चाहिए। अर्थात,
$ \lim\limits_{x \to 1^{+}} f(x)=3 . $
लेकिन फिर बाईं ओर और दाईं ओर के सीमांकन समान हो जाते हैं और इसलिए
$ \lim\limits_{x \to 1^{-}} f(x)=\lim\limits_{x \to 1^{+}} f(x)=\lim\limits_{x \to 1} f(x)=3 . $
चित्र 12.7 में दिए गए फलन के ग्राफ हमारे सीमा के बारे में अपने निष्कर्ष को मजबूत करते हैं। यहाँ, हम ध्यान रखते हैं कि एक दिए गए बिंदु पर फलन के मान और इसकी सीमा अलग-अलग हो सकते हैं (हालांकि दोनों परिभाषित हो सकते हैं)।

चित्र 12.7
12.3.1 सीमा का बीजगणित
ऊपर के चित्रों में हमने देखा है कि सीमा की प्रक्रिया जो भी सीमा और फलन अच्छी तरह से परिभाषित हों, जोड़, घटाव, गुणन और विभाजन के साथ संगत होती है। यह एक संयोचन नहीं है। वास्तव में, नीचे हम इन्हें एक प्रमेय के रूप में औपचारिक रूप से स्थापित करते हैं, बिना साबित किए।
प्रमेय 1 मान लीजिए $f$ और $g$ दो फलन हैं जैसे कि दोनों $\lim\limits_{x \to a} f(x)$ और $\lim\limits_{x \to a} g(x)$ मौजूद हैं। तब
(i) दो फलनों के योग की सीमा फलनों की सीमाओं के योग के बराबर होती है, अर्थात,
$ \lim\limits_{x \to a}[f(x)+g(x)]=\lim\limits_{x \to a} f(x)+\lim\limits_{x \to a} g(x) . $
(ii) दो फलनों के अंतर की सीमा फलनों की सीमाओं के अंतर के बराबर होती है, अर्थात,
$ \lim\limits_{x \to a}[f(x)-g(x)]=\lim\limits_{x \to a} f(x)-\lim\limits_{x \to a} g(x) . $
(iii) दो फलनों के गुणन के सीमा के लिए, फलनों की सीमाओं के गुणन के बराबर होता है, अर्थात,
$ \lim\limits_{x \to a}[f(x) \cdot g(x)]=\lim\limits_{x \to a} f(x) . \lim\limits_{x \to a} g(x) . $
(iv) दो फलनों के अनुपात की सीमा, फलनों की सीमाओं के अनुपात के बराबर होती है (जबकि हर शून्य न हो), अर्थात,
$ \lim\limits_{x \to a} \dfrac{f(x)}{g(x)}=\dfrac{\lim\limits_{x \to a} f(x)}{\lim\limits_{x \to a} g(x)} $
नोट - विशेष रूप से (iii) के एक विशेष मामला है, जब $g$ एक नियत फलन हो जिसके लिए $g(x)=\lambda$, कुछ वास्तविक संख्या $\lambda$ के लिए, हम लिख सकते हैं
$ \lim\limits_{x \to a}[(\lambda \cdot f)(x)]=\lambda \cdot \lim\limits_{x \to a} f(x) . $
अगले दो उपविभागों में, हम देखेंगे कि इस प्रमेय का उपयोग करके विशेष प्रकार के फलनों के सीमा कैसे गणना की जा सकती है।
12.3.2 बहुपद और परिमेय फलन के सीमा
एक फलन $f$ को डिग्री $n$ के बहुपद फलन कहा जाता है यदि $f(x)=a_0+a_1 x+a_2 x^{2}+\ldots+a_n x^{n}$, जहाँ $a_1$ वास्तविक संख्याएँ हैं और $a_n \neq 0$ कुछ प्राकृतिक संख्या $n$ के लिए।
हम जानते हैं कि $\lim\limits_{x \to a} x=a$। अतः
$ \lim\limits_{x \to a} x^{2}=\lim\limits_{x \to a}(x \cdot x)=\lim\limits_{x \to a} x \cdot \lim\limits_{x \to a} x=a \cdot a=a^{2} $
एक आसान प्रेरण आधारित अभ्यास हमें बताता है कि
$ \lim\limits_{x \to a} x^{n}=a^{n} $
अब, मान लीजिए $f(x)=a_0+a_1 x+a_2 x^{2}+\ldots+a_n x^{n}$ एक बहुपदीय फलन है। हमें प्रत्येक $a_0, a_1 x, a_2 x^{2}, \ldots, a_n x^{n}$ को एक फलन के रूप में सोचते हुए, हम लिख सकते हैं:
$ \begin{aligned} \lim\limits_ {x \to a} f(x) & =\lim\limits_ {x \to a}[a_ 0+a_ 1 x+a_ 2 x^{2}+\ldots+a_ {n} x^{n}] \\
$$ \begin{aligned} & =\lim\limits_ {x \to a} a_ 0+\lim\limits_ {x \to a} a_ 1 x+\lim\limits_ {x \to a} a_ 2 x^{2}+\ldots+\lim\limits_ {x \to a} a_ {n} x^{n} \\ & =a_ 0+a_ 1 \lim\limits_ {x \to a} x+a_ 2 \lim\limits_ {x
$ \lim\limits_{x \to a} f(x)=\lim\limits_{x \to a} \dfrac{g(x)}{h(x)}=\dfrac{\lim\limits_{x \to a} g(x)}{\lim\limits_{x \to a} h(x)}=\dfrac{g(a)}{h(a)} $
हालांकि, यदि $h(a)=0$, तो दो स्थितियाँ हो सकती हैं - (i) जब $g(a) \neq 0$ और (ii) जब $g(a)=0$. पहले मामले में हम कहते हैं कि सीमा में अस्तित्व नहीं है। दूसरे मामले में हम $g(x)=(x-a)^{k} g_1(x)$ लिख सकते हैं, जहाँ $k$ व्यंजक $g(x)$ में $(x-a)$ की घातों की अधिकतम घात है। इसी तरह, $h(x)=(x-a)^{l} h_1(x)$ लिखा जा सकता है क्योंकि $h(a)=0$ है। अब, यदि $k>l$, तो हम लिख सकते हैं
$ \lim\limits_{x \to a} f(x)=\dfrac{\lim\limits_{x \to a} g(x)}{\lim\limits_{x \to a} h(x)}=\dfrac{\lim\limits_{x \to a}(x-a)^{k} g_1(x)}{\lim\limits_{x \to a}(x-a)^{l} h_1(x)} $
$
$ =\dfrac{\lim\limits_{x \to a}(x-a)^{(k-l)} g_1(x)}{\lim\limits_{x \to a} h_1(x)}=\dfrac{0 . g_1(a)}{h_1(a)}=0 $
यदि $k < l$, सीमा परिभाषित नहीं है।
उदाहरण 1 सीमाएं ज्ञात कीजिए:
(i) $\lim\limits_{x \to 1}\left[x^{3}-x^{2}+1\right] \quad$
(ii) $\lim\limits_{x \to 3}\left[x(x+1)\right]$
(iii) $\lim\limits_{x \to-1}\left[1+x+x^{2}+\ldots+x^{10}\right]$.
हल आवश्यक सीमाएं कुछ बहुपदीय फलनों की सीमाएं हैं। इसलिए सीमाएं निर्धारित बिंदुओं पर फलन के मान हैं। हम लेते हैं
(i) $\lim\limits_{x \to 1}\left[x^{3}-x^{2}+1 \right]=1^{3}-1^{2}+1=1$
(ii) $\lim\limits_{x \to 3}\left[x(x+1)\right]=3(3+1)=3(4)=12$
(iii) $\lim\limits_{x \to-1}\left[1+x+x^{2}+\ldots+x^{10}\right]=1+(-1)+(-1)^{2}+\ldots+(-1)^{10}$
उदाहरण 2 सीमाएं खोजें:
(i) $\lim\limits_{x \to 1}\left[\dfrac{x^{2}+1}{x+100}\right]$
(ii) $\lim\limits_{x \to 2}\left[\dfrac{x^{3}-4 x^{2}+4 x}{x^{2}-4}\right]$
(iii) $\lim\limits_{x \to 2}\left[\dfrac{x^{2}-4}{x^{3}-4 x^{2}+4 x}\right]$
(iv) $\lim\limits_{x \to 2}\left[\dfrac{x^{3}-2 x^{2}}{x^{2}-5 x+6}\right]$
(v) $\lim\limits_{x \to 1}\left[\dfrac{x-2}{x^{2}-x}-\dfrac{1}{x^{3}-3 x^{2}+2 x}\right]$.
हल सभी फ़ंक्शन तर्कसंगत फ़ंक्शन हैं। इसलिए, हम सबसे पहले इन फ़ंक्शन को निर्धारित बिंदुओं पर मूल्यांकन करते हैं। यदि यह $\dfrac{0}{0}$ के रूप में हो, तो हम उन कारकों को खत्म करके फ़ंक्शन को फिर से लिखने की कोशिश करते हैं जो सीमा के $\dfrac{0}{0}$ के रूप में होने के कारण हैं।
(i) हमें $\lim\limits_{x \to 1} \dfrac{x^{2}+1}{x+100}=\dfrac{1^{2}+1}{1+100}=\dfrac{2}{101}$ मिलता है।
(ii) 2 पर फ़ंक्शन का मूल्यांकन करने पर, यह $\dfrac{0}{0}$ के रूप में होता है।
इसलिए $\quad \lim\limits_{x \to 2} \dfrac{x^{3}-4 x^{2}+4 x}{x^{2}-4}=\lim\limits_{x \to 2} \dfrac{x(x-2)^{2}}{(x+2)(x-2)}$
$ \begin{aligned} & =\lim\limits_{x \to 2} \dfrac{x(x-2)}{(x+2)} \quad \quad \quad \quad \text{जब } x \neq 2 \\ & =\dfrac{2(2-2)}{2+2}=\dfrac{0}{4}=0 . \end{aligned} $
(iii) 2 पर फलन का मूल्यांकन करने पर, हमें $\dfrac{0}{0}$ के रूप में प्राप्त होता है।
इसलिए $\quad \lim\limits_{x \to 2} \dfrac{x^{2}-4}{x^{3}-4 x^{2}+4 x}=\lim\limits_{x \to 2} \dfrac{(x+2)(x-2)}{x(x-2)^{2}}$
$ =\lim\limits_{x \to 2} \dfrac{(x+2)}{x(x-2)}=\dfrac{2+2}{2(2-2)}=\dfrac{4}{0}
$
जो परिभाषित नहीं है।
(iv) 2 पर फलन का मूल्यांकन करने पर, हमें $\dfrac{0}{0}$ के रूप में प्राप्त होता है।
इसलिए $\quad \lim\limits_{x \to 2} \dfrac{x^{3}-2 x^{2}}{x^{2}-5 x+6}=\lim\limits_{x \to 2} \dfrac{x^{2}(x-2)}{(x-2)(x-3)}$
$ =\lim\limits_{x \to 2} \dfrac{x^{2}}{(x-3)}=\dfrac{(2)^{2}}{2-3}=\dfrac{4}{-1}=-4 . $
(v) सबसे पहले, हम फलन को एक परिमेय फलन के रूप में लिखते हैं।
$ \begin{aligned} {\left[\dfrac{x-2}{x^{2}-x}-\dfrac{1}{x^{3}-3 x^{2}+2 x}\right] } & =\left[\dfrac{x-2}{x(x-1)}-\dfrac{1}{x(x^{2}-3 x+2)}\right] \\
$$ \begin{aligned} & =\left[\dfrac{x-2}{x(x-1)}-\dfrac{1}{x(x-1)(x-2)}\right] \\ & =\left[\dfrac{x^{2}-4 x+4-1}{x(x-1)(x-2)}\right] \\ & =\dfrac{x^{2}-4 x+3}{x(x-1)(x-2)} \end{aligned} $$
फलन को 1 पर मूल्यांकन करने पर, इसके रूप $\dfrac{0}{0}$ में प्राप्त होता है।
अतः $\quad \lim\limits_{x \to 1}\left[\dfrac{x^{2}-2}{x^{2}-x}-\dfrac{1}{x^{3}-3 x^{2}+2 x}\right]=\lim\limits_{x \to 1} \dfrac{x^{2}-4 x+3}{x(x-1)(x-2)}$
$ \begin{aligned} & =\lim\limits_{x \to 1} \dfrac{(x-3)(x-1)}{x(x-1)(x-2)} \\ & =\lim\limits_{x \to 1} \dfrac{x-3}{x(x-2)}=\dfrac{1-3}{1(1-2)}=2 . \end{aligned} $$
\end{aligned} $
हम यह ध्यान रखते हैं कि हम उपरोक्त मूल्यांकन में $(x-1)$ का अंश विभाजित कर सकते हैं क्योंकि $x \neq 1$ है।
अगले उपयोग के लिए एक महत्वपूर्ण सीमा के मूल्यांकन को नीचे एक प्रमेय के रूप में दिया गया है।
प्रमेय 2 किसी भी धनात्मक पूर्णांक $n$ के लिए,
$ \lim\limits_{x \to a} \dfrac{x^{n}-a^{n}}{x-a}=n a^{n-1} $
टिप्पणी उपरोक्त प्रमेय में सीमा के व्यंजक के लिए $n$ कोई भी परिमेय संख्या हो सकती है और $a$ धनात्मक हो सकता है।
उपपत्ति $(x^{n}-a^{n})$ को $(x-a)$ से विभाजित करने पर, हम देखते हैं कि
$ x^{n}-a^{n}=(x-a)(x^{n-1}+x^{n-2} a+x^{n-3} a^{2}+\ldots+x a^{n-2}+a^{n-1}) $
$ \begin{aligned} \text{अतः, }\quad \lim\limits_{x \to a} \dfrac{x^{n}-a^{n}}{x-a}& =\lim\limits_{x \to a}(x^{n-1}+x^{n-2} a+x^{n-3} a^{2}+\ldots+x a^{n-2}+a^{n-1}) \\ & =a^{n-1}+a a^{n-2}+\ldots+a^{n-2}(a)+a^{n-1} \\ & =a^{n-1}+a^{n-1}+\ldots+a^{n-1}+a^{n-1}(n \text{ पद }) \\ & =n a^{n-1} \end{aligned} $
उदाहरण 3 मूल्यांकन करें:
(i) $\lim\limits_{x \to 1} \dfrac{x^{15}-1}{x^{10}-1}$
(ii) $\lim\limits_{x \to 0} \dfrac{\sqrt{1+x}-1}{x}$
हल (i) हमारे पास है
$ \begin{aligned} \lim\limits_{x \to 1} \dfrac{x^{15}-1}{x^{10}-1} & =\lim\limits_{x \to 1}\left[\dfrac{x^{15}-1}{x-1} \div \dfrac{x^{10}-1}{x-1}\right] \\ & =\lim\limits_{x \to 1}\left[\dfrac{x^{15}-1}{x-1}\right] \div \lim\limits_{x \to 1}\left[\dfrac{x^{10}-1}{x-1}\right] \\ & =15(1)^{14} \div 10(1)^{9} \text{ (ऊपर के प्रमेय के अनुसार) } \\ & =15 \div 10=\dfrac{3}{2} \end{aligned} $
(ii) मान लीजिए $y=1+x$, तो $y \to 1$ जब $x \to 0$।
$ \begin{aligned} \text{तब} \quad \lim\limits_{x \to 0} \dfrac{\sqrt{1+x}-1}{x}& =\lim\limits_{y \to 1} \dfrac{\sqrt{y}-1}{y-1} \\
$$ \begin{aligned} & =\lim\limits_{y \to 1} \dfrac{y^{\dfrac{1}{2}}-1^{\dfrac{1}{2}}}{y-1} \\ & =\dfrac{1}{2}(1)^{\dfrac{1}{2}-1}(\text{ by the remark above })=\dfrac{1} {2} \end{aligned} $$
12.4 त्रिकोणमितीय फलनों के सीमा
कुछ त्रिकोणमितीय फलनों के सीमा की गणना करते समय निम्नलिखित तथ्य (जो कि प्रमेय के रूप में दिए गए हैं) उपयोगी होते हैं।
प्रमेय 3 मान लीजिए $f$ और $g$ दो वास्तविक मान फलन हैं जिनके एक ही प्रांत है और जिनके लिए प्रांत के सभी $x$ के लिए $f(x) \leq g(x)$ हो। यदि किसी $a$ के लिए $\lim\limits_{x \to a} f(x)$ और $\lim\limits_{x \to a} g(x)$ दोनों अस्तित्व में हों, तो $\lim\limits_{x \to a} f(x) \leq \lim\limits_{x \to a} g(x)$ होता है। यह चित्र 12.8 में दिखाया गया है।

चित्र 12.8
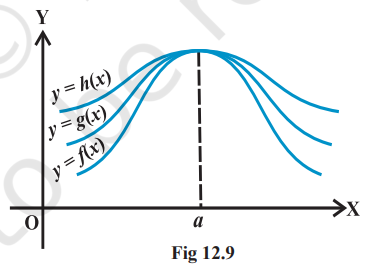
प्रमेय 4 (कांटा प्रमेय) मान लीजिए $f$, $g$ और $h$ वास्तविक फलन हैं जैसे कि $f(x) \leq g(x) \leq h(x)$ सभी $x$ के लिए सामान्य परिाषा के डोमेन में। किसी वास्तविक संख्या $a$ के लिए, यदि $\lim\limits_{x \to a} f(x)=l=\lim\limits_{x \to a} h(x)$, तो $\lim\limits_{x \to a} g(x)=l$। यह चित्र 12.9 में दिखाया गया है।
ऊपर दिए गए एक सुंदर ज्यामितीय प्रमाण त्रिकोणमितीय फलनों के बीच निम्नलिखित महत्वपूर्ण असमानुपात के संबंध के लिए है।
$ \cos x < \dfrac{\sin x}{x} < 1 \quad \text{ जब } 0 < |x| < \dfrac{\pi}{2} \quad \quad \quad \quad \quad ({}^*) $
प्रमाण हम जानते हैं कि $\sin (-x)=-\sin x$ और $\cos (-x)=\cos x$। अतः, $0 < x < \dfrac{\pi}{2}$ के लिए असमानुपात के प्रमाण करना पर्याप्त है।
In आकृति 12.10, $O$ इकाई वृत्त केंद्र है जैसे कि कोण AOC $x$ रेडियन है और $0 < x < \dfrac{\pi}{2}$. रेखाखंड B A और $CD$ $OA$ पर लम्ब हैं। इसके अतिरिक्त, $AC$ को मिलाइए। तब

आकृति 13.10
$\triangle OAC$ का क्षेत्रफल < क्षेत्रफल त्रिज्यखंड $OAC$ < $\triangle OAB$ का क्षेत्रफल।
अर्थात, $\quad \dfrac{1}{2} OA . CD < \dfrac{x}{2 \pi} . \pi .(OA)^{2} < \dfrac{1}{2} OA . AB$।
i.e., $\quad CD < x . OA < AB$.
$\triangle OCD$ से,
$ \sin x=\dfrac{CD}{OA}(\text{ क्योंकि } OC=OA) \text{ और इसलिए } CD=OA \sin x \text{। इसके अतिरिक्त } \tan x=\dfrac{AB}{OA} \text{ और } $
इसलिए $\quad AB=OA \cdot \tan x$. इस प्रकार
$ \text{ OA } \sin x<\text{ OA. } x < \text{ OA. } \tan x . $
क्योंकि OA की लंबाई धनात्मक है, हमारे पास
$ \sin x < x < \tan x \text{। } $
क्योंकि $0 < x < \dfrac{\pi}{2}, \sin x$ धनात्मक है और इसलिए सभी ओर $\sin x$ से विभाजित करने पर हमारे पास
$1 < \dfrac{x}{\sin x}<\dfrac{1}{\cos x} . \quad$ सभी ओर विपरीत लेने पर हमारे पास
$ \cos x<\dfrac{\sin x}{x}<1 $
जो प्रमेय के साबित करने को पूरा करता है।
प्रमेय 5 निम्नलिखित दो महत्वपूर्ण सीमाएं हैं।
(i) $\lim\limits_{x \to 0} \dfrac{\sin x}{x}=1$।
(ii) $\lim\limits_{x \to 0} \dfrac{1-\cos x}{x}=0$।
साबित (i) (*) में असमानुपात कहता है कि फ़ंक्शन $\dfrac{\sin x}{x}$ फ़ंक्शन $\cos x$ और एक स्थिर फ़ंक्शन के बीच संकुचित होता है, जो मान 1 लेता है।
इसके अतिरिक्त, क्योंकि $\lim\limits_{x \to 0} \cos x=1$, हम देखते हैं कि प्रमेय के (i) के साबित करने के लिए संकुचित प्रमेय द्वारा साबित कर दिया गया है।
(ii) को सिद्ध करने के लिए, हम त्रिकोणमितीय सर्वसमिका $1-\cos x=2 \sin ^{2}\left(\dfrac{x}{2}\right)$ को याद करते हैं।
तब
$ \begin{aligned} \lim\limits_{x \to 0} \dfrac{1-\cos x}{x} & =\lim\limits_{x \to 0} \dfrac{2 \sin ^{2}\left(\dfrac{x}{2}\right)}{x}=\lim\limits_{x \to 0} \dfrac{\sin \left(\dfrac{x}{2}\right)}{\dfrac{x}{2}} \cdot \sin \left(\dfrac{x}{2}\right) \\ & =\lim\limits_{x \to 0} \dfrac{\sin \left(\dfrac{x}{2}\right)}{\dfrac{x}{2}} \cdot \lim\limits_{x \to 0} \sin \left(\dfrac{x}{2}\right)=1.0=0
\end{aligned} $
ध्यान दें कि हमने $x \to 0$ के बराबर होने के तथ्य का अप्रत्यक्ष रूप से उपयोग किया है $\dfrac{x}{2} \to 0$। इसे वैध बनाने के लिए $y=\dfrac{x}{2}$ रख सकते हैं।
उदाहरण 4 मूल्यांकन करें:
(i) $\lim\limits_{x \to 0} \dfrac{\sin 4 x}{\sin 2 x}$
(ii) $\lim\limits_{x \to 0} \dfrac{\tan x}{x}$
हल $ \begin{aligned} \text{(i)} \quad \lim\limits_{x \to 0} \dfrac{\sin 4 x}{\sin 2 x} & =\lim\limits_{x \to 0}\left[\dfrac{\sin 4 x}{4 x} \cdot \dfrac{2 x}{\sin 2 x} \cdot 2 \right] \\ & =2 \cdot \lim\limits_{x \to 0}\left[\dfrac{\sin 4 x}{4 x}\right] \div \left[\dfrac{\sin 2 x}{2 x}\right] \\
& =2 \cdot \lim\limits_{4 x \to 0}\left[\dfrac{\sin 4 x}{4 x}\right] \div \lim\limits_{2 x \to 0}\left[\dfrac{\sin 2 x}{2 x}\right] \\ & =2 \cdot 1 \cdot 1=2(\text{ जैसे } x \to 0,4 x \to 0 \text{ और } 2 x \to 0) \end{aligned} $
(ii) हमें $\lim\limits_{x \to 0} \dfrac{\tan x}{x}=\lim\limits_{x \to 0} \dfrac{\sin x}{x \cos x}=\lim\limits_{x \to 0} \dfrac{\sin x}{x} \cdot \lim\limits_{x \to 0} \dfrac{1}{\cos x}=1.1=1$
लिमिट के मूल्यांकन के दौरान ध्यान में रखने वाला एक सामान्य नियम निम्नलिखित है। मान लीजिए कि लिमिट $\lim\limits_{x \to a} \dfrac{f(x)}{g(x)}$ मौजूद है और हम इसका मूल्यांकन करना चाहते हैं। सबसे पहले हम $f(a)$ और $g(a)$ के मूल्य की जांच करते हैं। यदि दोनों 0 हों, तो हम देखते हैं कि कौन सा गुणनखंड शब्दों को शून्य कर रहा है, अर्थात, हम देखते हैं कि क्या हम $f(x)=f_1(x) f_2(x)$ लिख सकते हैं ताकि $f_1(a)=0$ और $f_2(a) \neq 0$ हो। इसी तरह, हम $g(x)=g_1(x) g_2(x)$ लिखते हैं, जहां $g_1(a)=0$ और $g_2(a) \neq 0$ हो। $f(x)$ और $g(x)$ से उभयनिष्ठ गुणनखंड को बाहर ले जाएं (यदि संभव हो) और लिखें
$\quad \quad \quad \quad \dfrac{f(x)}{g(x)}=\dfrac{p(x)}{q(x)}, \text{ where } q(x) \neq 0 $
तब $\quad \quad \lim\limits_{x \to a} \dfrac{f(x)}{g(x)}=\dfrac{p(a)}{q(a)}$.
अभ्यास 12.1
निम्नलिखित सीमाएँ अभ्यास 1 से 22 तक ज्ञात कीजिए।
1. $\lim\limits_{x \to 3} x+3$
उत्तर दिखाएँ
उत्तर :
$\lim _{x \to 3} x+3=3+3=6$
2. $\lim\limits_{x \to \pi}\left(x-\dfrac{22}{7}\right)$
उत्तर दिखाएँ
उत्तर :
$\lim _{x \to \pi}\left(x-\dfrac{22}{7}\right)=\left(\pi-\dfrac{22}{7}\right)$
3. $\lim\limits_{r \to 1} \pi r^{2}$
उत्तर दिखाएँ
उत्तर :
$\lim _{r \to 1} \pi r^{2}=\pi\left(1\right)^{2}=\pi$
4. $\lim\limits_{x \to 4} \dfrac{4 x+3}{x-2}$
उत्तर दिखाएँ
उत्तर :
$\lim _{x \to 4} \dfrac{4 x+3}{x-2}=\dfrac{4\left(4\right)+3}{4-2}=\dfrac{16+3}{2}=\dfrac{19}{2}$
5. $\lim\limits_{x \to-1} \dfrac{x^{10}+x^{5}+1}{x-1}$
उत्तर दिखाएँ
उत्तर :
$\lim _{x \to-1} \dfrac{x^{10}+x^{5}+1}{x-1}=\dfrac{\left(-1\right)^{10}+\left(-1\right)^{5}+1}{-1-1}=\dfrac{1-1+1}{-2}=-\dfrac{1}{2}$
6. $\lim\limits_{x \to 0} \dfrac{\left(x+1\right)^{5}-1}{x}$
उत्तर दिखाएँ
उत्तर :
$\lim _{x \to 0} \dfrac{\left(x+1\right)^{5}-1}{x}$
$ x+1=y $ रखें ताकि $ y^5 - $ 1 जब $x \to 0 $
इस प्रकार,
$\lim _{x \to 0} \dfrac{\left(x+1\right)^{5}-1}{x}=\lim _{y \to 1} \dfrac{y^{5}-1}{y-1}$
$\hspace{3cm}=\lim _{y \to 1} \dfrac{y^{5}-1^{5}}{y-1}$
$\hspace{3cm}=5 \cdot 1^{5-1}$ $\qquad\left[\because \ \ \lim _{x \to a} \dfrac{x^{n}-a^{n}}{x-a}=n a^{n-1}\right]$
$\hspace{3cm}=5$
$\therefore \ \ \lim _{x \to 0} \dfrac{\left(x+5\right)^{5}-1}{x}=5$
7. $\lim\limits_{x \to 2} \dfrac{3 x^{2}-x-10}{x^{2}-4}$
उत्तर दिखाएँ
उत्तर :
$ x=2 $ पर, दी गई परिमेय फलन का मान $\dfrac{0}{0}$ के रूप में आता है।
$ \begin{aligned}
\therefore \ \ \lim _{x \to 2} \dfrac{3 x^{2}-x-10}{x^{2}-4} & =\lim _{x \to 2} \dfrac{\left(x-2\right)\left(3 x+5\right)}{\left(x-2\right)\left(x+2\right)} \\ \\ & =\lim _{x \to 2} \dfrac{3 x+5}{x+2} \\ \\ & =\dfrac{3\left(2\right)+5}{2+2} \\ \\ & =\dfrac{11}{4} \end{aligned} $
8. $\lim\limits_{x \to 3} \dfrac{x^{4}-81}{2 x^{2}-5 x-3}$
उत्तर दिखाएं
Answer :
$x=2$ के लिए, दिए गए परिमेय फलन का मान $\dfrac{0}{0}$ के रूप में होता है।
$ \begin{aligned} \therefore \ \ \lim _{x \to 3} \dfrac{x^{4}-81}{2 x^{2}-5 x-3} & =\lim _{x \to 3} \dfrac{\left(x-3\right)\left(x+3\right)\left(x^{2}+9\right)}{\left(x-3\right)\left(2 x+1\right)} \\ \\ & =\lim _{x \to 3} \dfrac{\left(x+3\right)\left(x^{2}+9\right)}{2 x+1} \\ \\ & =\dfrac{\left(3+3\right)\left(3^{2}+9\right)}{2\left(3\right)+1} \\ \\ & =\dfrac{6 \times 18}{7} \\ \\ & =\dfrac{108}{7} \end{aligned} $
9. $\lim\limits_{x \to 0} \dfrac{a x+b}{c x+1}$
उत्तर दिखाएं
Answer :
$\lim _{x \to 0} \dfrac{a x+b}{c x+1}=\dfrac{a\left(0\right)+b}{c\left(0\right)+1}=b$
10. $\lim\limits_{z \to 1} \dfrac{z^{\frac{1}{3}}-1}{z^{\frac{1}{6}}-1}$
उत्तर दिखाएं
Answer :
$\lim _{z \to 1} \dfrac{z^{\frac{1}{3}}-1}{z^{\frac{1}{6}}-1}$
$z=1$ के लिए, दिए गए फलन का मान $\frac{0}{0}$ के रूप में होता है
$z^{\frac{1}{6}}=x$ रखें ताकि $z ^{\frac{1}{6}}- 1 \text{ as } x\to 1 $
इसलिए,
$\lim _{z \to 1} \dfrac{z^{\frac{1}{3}}-1}{z^{\frac{1}{6}}-1}=\lim _{x \to 1} \dfrac{x^{2}-1}{x-1}$
$ \hspace{2.2cm}=\lim _{x \to 1} \dfrac{x^{2}-1^{2}}{x-1} $
$ \hspace{2.2cm}=2.1^{2-1} \quad\left[\because \ \ \lim _{x \to a} \dfrac{x^{n}-a^{n}}{x-a}=n a^{n-1}\right] $
$\hspace{2.2cm}=2$
$\therefore \ \ \lim _{z \to 1} \dfrac{z^{\frac{1}{3}}-1}{z^{\frac{1}{6}}-1}=2$
11. $\lim\limits_{x \to 1} \dfrac{a x^{2}+b x+c}{c x^{2}+b x+a}, a+b+c \neq 0$
उत्तर दिखाएं
उत्तर :
$ \begin{aligned} \lim _{x \to 1} \dfrac{a x^{2}+b x+c}{c x^{2}+b x+a} & =\dfrac{a\left(1\right)^{2}+b\left(1\right)+c}{c\left(1\right)^{2}+b\left(1\right)+a} \\ \\ & =\dfrac{a+b+c}{a+b+c} \\ \\ & =1 \quad\left[a+b+c \neq 0\right] \end{aligned} $
12. $\lim\limits_{x \to-2} \dfrac{\frac{1}{x}+\frac{1}{2}}{x+2}$
उत्तर दिखाएं
उत्तर :
$\lim _{x \to-2} \dfrac{\frac{1}{x}+\frac{1}{2}}{x+2}$
$ x = -2 $ पर, दी गई फलन का मान $\frac{0}{0}$ के रूप में होता है।
अब,
$ \begin{aligned} \lim _{x \to-2} \dfrac{\frac{1}{x}+\frac{1}{2}}{x+2} & =\lim _{x \to-2} \dfrac{\left(\frac{2+x}{2 x}\right)}{x+2} \\ \\ & =\lim _{x \to-2} \frac{1}{2 x} \\ \\ & =\frac{1}{2\left(-2\right)}=\frac{-1}{4} \end{aligned} $
13. $ \ \lim\limits_{x \to 0}\left(\dfrac{\sin a x}{b x}\right)$
उत्तर दिखाएं
उत्तर :
$\lim _{x \to 0} \dfrac{\sin a x}{b x}$
$ x = 0 $ पर, दी गई फलन का मान $\dfrac{0}{0}$ के रूप में होता है।
अब,
$\lim _{x \to 0} \dfrac{\sin a x}{b x}=\lim _{x \to 0} \dfrac{\sin a x}{a x} \times \dfrac{a x}{b x}$
$\hspace{2.2cm}=\lim _{x \to 0}\left(\dfrac{\sin a x}{a x}\right) \times\left(\dfrac{a}{b}\right)$
$\hspace{2.2cm}=\dfrac{a}{b} \lim _{a x \to 0}\left(\dfrac{\sin a x}{a x}\right) \quad\left[x \to 0 \Rightarrow a x \to 0\right]$
$\hspace{2.2cm}=\dfrac{a}{b} \times 1 \quad\left[\because \ \ \ \lim _{y \to 0} \dfrac{\sin y}{y}=1\right]$
$\hspace{2.2cm}=\dfrac{a}{b}$
14. $\lim\limits_{x \to 0} \dfrac{\sin a x}{\sin b x}, a, b \neq 0$
उत्तर दिखाएं
उत्तर :
$\lim _{x \to 0} \dfrac{\sin a x}{\sin b x}, a, b \neq 0$
$ x = 0 $ पर, दी गई फलन का मान $\dfrac{0}{0}$ के रूप में होता है।
अब,
$ \begin{aligned} \lim _{x \to 0} \dfrac{\sin a x}{\sin b x} & =\lim _{x \to 0} \dfrac{\left(\dfrac{\sin a x}{a x}\right) \times a x}{\left(\dfrac{\sin b x}{b x}\right) \times b x} \\ \\
& =\left(\dfrac{a}{b}\right) \times \dfrac{\lim _{a x \to 0}\left(\dfrac{\sin a x}{a x}\right)}{\lim _{b x \to 0}\left(\dfrac{\sin b x}{b x}\right)} \\ \\ & x \to 0 \Rightarrow a x \to 0 \ \text{ और } \ x \to 0 \Rightarrow b x \to 0 \\ \\ & =\left(\dfrac{a}{b}\right) \times \dfrac{1}{1} {\left[\because \ \ \ \lim _{y \to 0} \dfrac{\sin y}{y}=1\right]} \\ \\ & =\dfrac{a}{b} \end{aligned} $
15. $\lim\limits_{x \to \pi} \dfrac{\sin \left(\pi-x\right)}{\pi\left(\pi-x\right)}$
उत्तर दिखाएं
Answer :
$\lim _{x \to \pi} \dfrac{\sin \left(\pi-x\right)}{\pi\left(\pi-x\right)}$
यह देखा जाता है कि $x $ $\to$ $\pi \Rightarrow\left(\pi - x\right) \to 0 $
$ \begin{aligned} \therefore \ \ \lim _{x \to \pi} \dfrac{\sin \left(\pi-x\right)}{\pi\left(\pi-x\right)} & =\dfrac{1}{\pi} \lim _{\left(\pi-x\right) \to 0} \dfrac{\sin \left(\pi-x\right)}{\left(\pi-x\right)} \\ \\ & =\dfrac{1}{\pi} \times 1 \quad\left[\because \ \ \ \lim _{y \to 0} \dfrac{\sin y}{y}=1\right] \\ \\ & =\dfrac{1}{\pi} \end{aligned} $
16. $\lim\limits_{x \to 0} \dfrac{\cos x}{b-x}$
उत्तर दिखाएं
Answer :
$\lim _{x \to 0} \dfrac{\cos x}{\pi-x}=\dfrac{\cos 0}{\pi-0}=\dfrac{1}{\pi}$
17. $ \lim\limits_{x \to 0}\dfrac{\cos 2x-1}{\cos x-1} $
उत्तर दिखाएं
Answer :
$\lim _{x \to 0} \dfrac{\cos 2 x-1}{\cos x-1}$
$x=0$ पर, दी गई फलन का मान $\dfrac{0}{0}$ के रूप में होता है
अब,
$ \begin{aligned} \lim _{x \to 0} \dfrac{\cos 2 x-1}{\cos x-1} & =\lim _{x \to 0} \dfrac{1-2 \sin ^{2} x-1}{1-2 \sin ^{2} \frac{x}{2}-1} \quad\left[\because \ \ \ \cos x=1-2 \sin ^{2} \dfrac{x}{2}\right] \\ \\ & =\lim _{x \to 0} \dfrac{\sin ^{2} x}{\sin ^{2} \frac{x}{2}}=\lim _{x \to 0} \dfrac{\left(\frac{\sin ^{2} x}{x^{2}}\right) \times x^{2}}{\left(\dfrac{\sin ^{2} \frac{x}{2}}{\left(\frac{x}{2}\right)^{2}}\right) \times \frac{x^{2}}{4}} \\ \\
& =4 \dfrac{\lim _{x \to 0}\left(\frac{\sin ^{2} x}{x^{2}}\right)}{\lim _{x \to 0}\left(\dfrac{\sin ^{2} \frac{x}{2}}{\left(\frac{x}{2}\right)^{2}}\right)} \\ \\ & =4 \dfrac{\left(\lim _{x \to 0} \frac{\sin x}{x}\right)^{2}}{\left(\lim _{\frac{x}{2} \to 0} \dfrac{\sin \frac{x}{2}}{\frac{x}{2}}\right)^{2}} \quad\left[x \to 0 \Rightarrow \dfrac{x}{2} \to 0\right] \\ \\ & =4 \left(\dfrac{1^{2}}{1^{2}}\right) \qquad\left[\because \ \ \ \lim _{y \to 0} \frac{\sin y}{y}=1\right] \\ \\ & =4 \end{aligned} $
18. $\lim\limits_{x \to 0} \dfrac{ax+xcosx}{b\sin x}$,
उत्तर दिखाएं
Answer :
$\lim _{x \to 0} \dfrac{a x+x \cos x}{b \sin x}$
$x=0$ के लिए, दी गई फलन का मान $\dfrac{0}{0}$ के रूप में ले लिया जाता है।
अब,
$ \begin{aligned} \lim _{x \to 0} \dfrac{a x+x \cos x}{b \sin x} & =\dfrac{1}{b} \lim _{x \to 0} \dfrac{x\left(a+\cos x\right)}{\sin x} \\ \\ & =\dfrac{1}{b} \lim _{x \to 0}\left(\dfrac{x}{\sin x}\right) \times \lim _{x \to 0}\left(a+\cos x\right) \\ \\ & =\dfrac{1}{b} \times \dfrac{1}{\left(\lim _{x \to 0} \dfrac{\sin x}{x}\right)} \times \lim _{x \to 0}\left(a+\cos x\right) \\ \\ & =\dfrac{1}{b} \times\left(a+\cos 0\right) \quad\left[\lim _{x \to 0} \dfrac{\sin x}{x}=1\right] \\ \\ & =\dfrac{a+1}{b} \end{aligned} $
19. $\lim\limits_{x \to 0}x\sec x $
उत्तर दिखाएं
Answer :
$\lim _{x \to 0} x \sec x=\lim _{x \to 0} \dfrac{x}{\cos x}=\dfrac{0}{\cos 0}=\dfrac{0}{1}=0$
20. $\lim\limits_{x \to 0} \dfrac{\sin ax+bx}{ax+\sin bx}a,b,a+b\neq0,$
उत्तर दिखाएं
Answer :
$x=0$ के लिए, दी गई फलन का मान $\dfrac{0}{0}$ के रूप में ले लिया जाता है।
अब,
$ \begin{aligned} \lim _{x \to 0} \dfrac{\sin a x+b x}{a x+\sin b x} & =\lim _{x \to 0} \dfrac{\left(\dfrac{\sin a x}{a x}\right) a x+b x}{a x+b x\left(\dfrac{\sin b x}{b x}\right)} \\ \\ & =\dfrac{\left(\lim _{a x \to 0} \dfrac{\sin a x}{a x}\right) \times \lim _{x \to 0}\left(a x\right)+\lim _{x \to 0} b x}{\lim _{x \to 0} a x+\lim _{x \to 0} b x\left(\lim _{b x \to 0} \dfrac{\sin b x}{b x}\right)} \qquad\left[\because \ \ \text{ As } x \to 0 \Rightarrow a x \to 0 \text{ and } b x \to 0 \right] \\ \\
& =\dfrac{\lim _{x \to 0}\left(a x\right)+\lim _{x \to 0} b x}{\lim _{x \to 0} a x+\lim _{x \to 0} b x} \qquad\left[\because \ \ \lim _{x \to 0} \dfrac{\sin x}{x}=1\right] \\ \\ & =\dfrac{\lim _{x \to 0}\left(a x+b x\right)}{\lim _{x \to 0}\left(a x+b x\right)} \\ \\ & =\lim _{x \to 0}\left(1\right) \\ \\ & =1 \end{aligned} $
21. $ \lim\limits_{x \to 0}\left(\text{cosec} \ x -\cot x\right) $
उत्तर दिखाएं
Answer :
$x=0$ पर, दी गई फलन का मान $\infty-\infty$ के रूप में होता है।
अब,
$ \begin{aligned} \lim _{x \to 0}\left(\text{cosec} \ x-\cot x\right) & =\lim _{x \to 0}\left(\dfrac{1}{\sin x}-\dfrac{\cos x}{\sin x}\right) \\ \\ & =\lim _{x \to 0}\left(\dfrac{1-\cos x}{\sin x}\right) \\ \\ & =\lim _{x \to 0} \dfrac{\left(\dfrac{1-\cos x}{x}\right)}{\left(\dfrac{\sin x}{x}\right)} \\ \\ & =\dfrac{\lim _{x \to 0} \dfrac{1-\cos x}{x}}{\lim _{x \to 0} \dfrac{\sin x}{x}} \qquad\left[\because \ \ \lim _{x \to 0} \dfrac{1-\cos x}{x}=0 \text{ and } \lim _{x \to 0} \dfrac{\sin x}{x}=1\right] \\ \\ & =\dfrac{0}{1} =0 \end{aligned} $
22. $\lim\limits_{x \to ({\pi}/{2})} \dfrac{\tan 2 x}{x-\frac{\pi}{2}}$
उत्तर दिखाएं
Answer :
$\lim _{x \to ({\pi}/{2})} \dfrac{\tan 2 x}{x-\frac{\pi}{2}}$
$x=\dfrac{\pi}{2}$ पर, दी गई फलन का मान $\dfrac{0}{0}$ के रूप में होता है।
अब, $x-\dfrac{\pi}{2}=y \quad x \to \dfrac{\pi}{2}, y \to 0$ को रखें
$\therefore \ \ \lim _{x \to ({\pi}/{2})} \dfrac{\tan 2 x}{x-\frac{\pi}{2}} =\lim _{y \to 0} \dfrac{\tan 2\left(y+\frac{\pi}{2}\right)}{y} $
$\hspace{2.8cm} =\lim _{y \to 0} \dfrac{\tan \left(\pi+2 y\right)}{y} \quad\left[\because \ \ \tan \left(\pi+2 y\right)=\tan 2 y\right] $
$\hspace{2.8cm} =\lim _{y \to 0} \dfrac{\tan 2 y}{y} $
$\hspace{2.8cm} =\lim _{y \to 0} \dfrac{\sin 2 y}{y\cdot\cos 2 y} $
$\hspace{2.8cm} =\lim _{y \to 0}\left(\dfrac{\sin 2 y}{2 y} \times \dfrac{2}{\cos 2 y}\right) $
$\hspace{2.8cm} =\left(\lim _{2 y \to 0} \dfrac{\sin 2 y}{2 y}\right) \times \lim _{y \to 0}\left(\dfrac{2}{\cos 2 y}\right) \quad\left[\because \ \ \lim _{x \to 0} \dfrac{\sin x}{x}=1\right] $
$\hspace{2.8cm} =1 \times \dfrac{2}{\cos 0} $
$\hspace{2.8cm} =1 \times \dfrac{2}{1} $
$\hspace{2.8cm} =2 $
23. $\lim\limits_{x \to 0} f\left(x\right)$ और $\lim\limits_{x \to 1} f\left(x\right)$ ज्ञात कीजिए, जहाँ $f\left(x\right)=\begin{cases} 2 x+3, & x \leq 0 \\ \\ 3\left(x+1\right), & x>0\end{cases} .$
उत्तर दिखाएं
Answer :
दिया गया फलन है
$f\left(x\right)= \begin{cases}2 x+3, & x \leq 0 \\ \\ 3\left(x+1\right), & x>0\end{cases}$
$\lim _{x \to 0^{-}} f\left(x\right)=\lim _{x \to 0}\left(2 x+3\right)=2\left(0\right)+3=3$
$\lim _{x \to 0^{+}} f\left(x\right)=\lim _{x \to 0} 3\left(x+1\right)=3\left(0+1\right)=3$
$\therefore \ \ \lim _{x \to 0^{-}} f\left(x\right)=\lim _{x \to 0^{+}} f\left(x\right)=\lim _{x \to 0} f\left(x\right)=3$
$\lim _{x \to 1^{-}} f\left(x\right)=\lim _{x \to 1} 3\left(x+1\right)=3\left(1+1\right)=6$ $\lim _{x \to 1^{+}} f\left(x\right)=\lim _{x \to 1} 3\left(x+1\right)=3\left(1+1\right)=6$
$\therefore \ \ \lim _{x \to 1^{-}} f\left(x\right)=\lim _{x \to 1^{+}} f\left(x\right)=\lim _{x \to 1} f\left(x\right)=6$
24. $\lim\limits_{x \to 1} f\left(x\right)$ ज्ञात कीजिए, जहाँ $f\left(x\right)= \begin{cases}x^{2}-1, & x \leq 1 \\ \\ -x^{2}-1, & x>1\end{cases}$
उत्तर दिखाएं
Answer :
दिया गया फलन है
$f\left(x\right)=\begin{cases} x^{2}-1, x \leq 1 \\ \\ -x^{2}-1, x>1 \end{cases} $
$\lim _{x \to 1^{-}} f\left(x\right)=\lim _{x \to 1}\left(x^{2}-1\right)=1^{2}-1=1-1=0$
$\lim _{x \to 1^{+}} f\left(x\right)=\lim _{x \to 1}\left(-x^{2}-1\right)=-1^{2}-1=-1-1=-2$
यह देखा गया है कि $\lim _{x \to 1^{-}} f\left(x\right) \neq \lim _{x \to 1^{+}} f\left(x\right)$
अतः, $\lim _{x \to 1} f\left(x\right)$ अस्तित्व नहीं रखता।
25. मान लीजिए $\lim\limits_{x \to 0} f\left(x\right)$, जहाँ $f\left(x\right)= \begin{cases}\dfrac{|x|}{x}, & x \neq 0 \\ \\ 0, & x=0\end{cases}$
उत्तर दिखाएं
उत्तर :
दी गई फलन है
$f\left(x\right)= \begin{cases}\dfrac{|x|}{x}, & x \neq 0 \\ \\ 0, & x=0\end{cases}$
$ \begin{matrix} \lim _{x \to 0^{-}} f\left(x\right) & =\lim _{x \to 0^{-}}\left(\dfrac{|x|}{x}\right) & \\ \\ & =\lim _{x \to 0}\left(\dfrac{-x}{x}\right) \quad & \\ \\ & =\lim _{x \to 0}\left(-1\right) \\ \\ & =-1 \\ \\ \lim _{x \to 0^{+}} f\left(x\right) & =\lim _{x \to 0^{+}}\left(\dfrac{|x|}{x}\right) & \\ \\ & =\lim _{x \to 0}\left(\dfrac{x}{x}\right) \\ \\ & =\lim _{x \to 0}\left(1\right) \\ \\ & =1 \end{matrix} $
यह देखा गया है कि $\lim _{x \to 0^{-}} f\left(x\right) \neq \lim _{x \to 0^{+}} f\left(x\right)$।
अतः, $\lim _{x \to 0} f\left(x\right)$ अस्तित्व नहीं रखता।
26. मान लीजिए $\lim\limits_ {x \to 0} f\left(x\right)$, जहाँ $f\left(x\right)=\begin{cases} \dfrac{x}{|x|}, & x \neq 0 \\ \\ 0, & x=0\end{cases} $
उत्तर दिखाएं
उत्तर :
दी गई फलन है
$ \begin{aligned} f\left(x\right) & = \begin{cases}\dfrac{x}{|x|}, & x \neq 0 \\ \\ 0, & x=0\end{cases} \\ \\ \lim _{x \to 0^{-}} f\left(x\right) & =\lim _{x \to 0^{-}}\left(\dfrac{x}{|x|}\right) \\ \\ & =\lim _{x \to 0}\left(\dfrac{x}{-x}\right) \quad\left[\text{ जब } x<0,|x|=-x\right] \\ \\ & =\lim _{x \to 0}\left(-1\right) \\ \\ & =-1 \\ \\ \lim _{x \to 0^{+}} f\left(x\right) & =\lim _{x \to 0^{+}}\left(\dfrac{x}{|x|}\right) \\ \\ & =\lim _{x \to 0}\left(\dfrac{x}{x}\right) \quad\left[\text{ जब } x>0,|x|=x\right] \\ \\ & =\lim _{x \to 0}\left(1\right) \\ \\ & =1 \end{aligned} $
यह देखा गया है कि $\lim _{x \to 0^{-}} f\left(x\right) \neq \lim _{x \to 0^{+}} f\left(x\right)$।
अतः, $\lim _{x \to 0} f\left(x\right)$ अस्तित्व नहीं रखता।
27. ज्ञात कीजिए $\lim\limits_{x \to 5} f\left(x\right)$, जहाँ $f\left(x\right)=|x|-5$
उत्तर दिखाएं
उत्तर :
दी गई फलन $f\left(x\right)=|x|-5$ है।
$ \begin{aligned} & \begin{aligned} \lim _{x \to 5^{-}} f\left(x\right) & =\lim _{x \to 5^{-}}\left[|x|-5\right] \\ \\ & =\lim _{x \to 5}\left(x-5\right) \quad \\ \\ & =5-5 \\ \\ & =0 \end{aligned} \\ \\ & \begin{aligned} \lim _{x \to 5^{+}} f\left(x\right) & =\lim _{x \to 5^{+}}\left(|x|-5\right) \\ \\ & =\lim _{x \to 5}\left(x-5\right) \quad \\ \\ & =5-5 \\ \\ & =0 \end{aligned} \\ \\ & \therefore \ \ \lim _{x \to 5^{-}} f\left(x\right)=\lim _{x \to 5^{+}} f\left(x\right)=0 \end{aligned} $
इसलिए, $\lim _{x \to 5} f\left(x\right)=0$
28. मान लीजिए $f\left(x\right)= \begin{cases}a+b x, & x<1 \\ \\ 4, & x=1 \\ \\ b-a x, & x>1\end{cases}$
और यदि $\lim\limits_{x \to 1} f\left(x\right)=f\left(1\right)$, तो $a$ और $b$ के संभावित मान क्या हैं ?
उत्तर दिखाएं
उत्तर :
दी गई फलन
$f\left(x\right)= \begin{cases}a+b x, & x<1 \\ \\ 4, & x=1 \\ \\ b-a x & x>1\end{cases}$
$\lim _{x \to 1^{-}} f\left(x\right)=\lim _{x \to 1}\left(a+b x\right)=a+b$
$\lim _{x \to 1^{+}} f\left(x\right)=\lim _{x \to 1}\left(b-a x\right)=b-a$
$f\left(1\right)=4$
दिया गया है कि $\lim _{x \to 1} f\left(x\right)=f\left(1\right)$।
$\therefore \ \ \lim _{x \to 1 ^{-}} f\left(x\right)=\lim _{x \to 1^{+}} f\left(x\right)=\lim _{x \to 1} f\left(x\right)=f\left(1\right)$
$\Rightarrow a+b=4$ और $b-a=4$
इन दोनों समीकरणों को हल करने पर हमें $a=0$ और $b=4$ प्राप्त होते हैं
इसलिए, $a$ और $b$ के संभावित मान क्रमशः 0 और 4 हैं
29. मान लीजिए $a_ 1, a_ 2, \ldots, a_ {n}$ निश्चित वास्तविक संख्याएँ हैं और एक फलन $f\left(x\right)=\left(x-a_ 1\right)\left(x-a 2\right) \ldots\left(x-a_ {n}\right)$ परिभाषित कीजिए
$x \to a_ 1$ के अग्रिम में $f\left(x\right)$ का मान क्या है? कुछ $a \neq a_ 1, a_ 2, \ldots, a_ {n}$ के लिए, $x \to a$ के अग्रिम में $f\left(x\right)$ का मान गणना कीजिए
उत्तर दिखाएँ
उत्तर :
दिए गए फलन है $f\left(x\right)=\left(x-a_1\right)\left(x-a_2\right) \ldots\left(x-a_n\right)$
$ \begin{aligned} \lim _{x \to a_1} f\left(x\right) & =\lim _{x \to a_1}\left[\left(x-a_1\right)\left(x-a_2\right) \ldots\left(x-a_n\right)\right] \\ \\ & =\left[\lim _{x \to a_1}\left(x-a_1\right)\right]\left[\lim _{x \to a_1}\left(x-a_2\right)\right] \ldots\left[\lim _{x \to a_1}\left(x-a_n\right)\right] \\ \\ & =\left(a_1-a_1\right)\left(a_1-a_2\right) \ldots\left(a_1-a_n\right)=0 \end{aligned} $
$\therefore \ \ \lim _{x \to a_1} f\left(x\right)=0$
अब,
$ \begin{aligned} \lim _{x \to a} f\left(x\right) & =\lim _{x \to a}\left[\left(x-a_1\right)\left(x-a_2\right) \ldots\left(x-a_n\right)\right] \\ \\ & =\left[\lim _{x \to a}\left(x-a_1\right)\right]\left[\lim _{x \to a}\left(x-a_2\right)\right] \ldots\left[\lim _{x \to a}\left(x-a_n\right)\right] \\ \\ & =\left(a-a_1\right)\left(a-a_2\right) \ldots .\left(a-a_n\right) \end{aligned} $
$\therefore \ \ \lim _{x \to a} f\left(x\right)=\left(a-a_1\right)\left(a-a_2\right) \ldots\left(a-a_n\right)$
30. यदि $ f\left(x\right)=\begin{cases} |x|+1, & x<0 \\ \\ 0, & x=0 \\ \\ |x|-1, & x>0\end{cases} .$
किस मान $\left(s\right)$ के लिए $\lim\limits_{x \to a} f\left(x\right)$ मौजूद होता है?
उत्तर दिखाएँ
उत्तर :
दिए गए फलन है $f\left(x\right)= \begin{cases}|x|+1, & x<0 \\ \\ 0, & x=0 \\ \\ |x|-1, & x>0\end{cases}$
जब $a=0$,
$ \begin{aligned} \lim _{x \to 0^{-}} f\left(x\right) & =\lim _{x \to 0^{-}}\left(|x|+1\right) \\ \\ & =\lim _{x \to 0}\left(-x+1\right) \quad\left[\text{ यदि } x<0,|x|=-x\right] \\ \\ & =(0+1) \\ \\ & =1 \end{aligned} $
$\lim _{x \to 0^{+}} f\left(x\right) =\lim _{x \to 0^{+}}\left(|x|-1\right) $
$\hspace{2.1cm} =\lim _{x \to 0}\left(x-1\right) \quad\left[\text{ यदि } x>0,|x|=x\right] $
$\hspace{2.1cm}=0-1 $
$\hspace{2.1cm} =-1 $
यहां देखा जाता है कि $\lim _{x \to 0^{-}} f\left(x\right) \neq \lim _{x \to 0^{+}} f\left(x\right)$
$\therefore \ \ \lim _{x \to 0} f\left(x\right)$ अस्तित्व में नहीं है।
जब $a<0$,
$ \begin{aligned} & \begin{aligned} \lim _{x \to a^{-}} f\left(x\right) & =\lim _{x \to a^{-}}\left(|x|+1\right) \\ \\ & =\lim _{x \to a}\left(-x+1\right) \quad\left[x<a<0 \Rightarrow|x|=-x\right] \\ \\ & =-a+1 \end{aligned} \\ \\ & \begin{aligned} \lim _{x \to a^{+}} f\left(x\right) & =\lim _{x \to a^{+}}\left(|x|+1\right) \\ \\ & =\lim _{x \to a}\left(-x+1\right) \quad\left[a<x<0 \Rightarrow|x|=-x\right] \\ \\ & =-a+1 \end{aligned} \\ \\ & \therefore \ \ \lim _{x \to a^{-}} f\left(x\right)=\lim _{x \to a^{+}} f\left(x\right)=-a+1 \end{aligned} $
इसलिए, $f\left(x\right)$ का सीमा $x=a$ पर अस्तित्व में है, जहां $a<0$ है।
जब $a>0$
$ \begin{aligned} \lim _{x \to a^{-}} f\left(x\right) & =\lim _{x \to a^{-}}\left(|x|-1\right) \\ \\ & =\lim _{x \to a}\left(x-1\right) \quad\left[0<x<a \Rightarrow|x|=x\right] \\ \\ & =a-1 \\ \\ \lim _{x \to a^{+}} f\left(x\right) & =\lim _{x \to a^{+}}\left(|x|-1\right) \\ \\ & =\lim _{x \to a}\left(x-1\right) \quad\left[0<a<x \Rightarrow|x|=x\right] \\ \\ & =a-1 \\ \\ & \therefore \ \ \lim _{x \to a^{-}} f\left(x\right)=\lim _{x \to a^{+}} f\left(x\right)=a-1 \end{aligned} $
इसलिए, $f\left(x\right)$ का सीमा $x=a$ पर अस्तित्व में है, जहां $a>0$ है।
इसलिए, $\lim _{x \to a} f\left(x\right)$ सभी $a \neq 0$ के लिए अस्तित्व में है
31. यदि फलन $f\left(x\right)$ संतुष्टि करता है $\lim\limits_{x \to 1} \dfrac{f\left(x\right)-2}{x^{2}-1}=\pi$, तो $\lim\limits_{x \to 1} f\left(x\right)$ का मूल्यांकन करें
उत्तर दिखाएं
Answer :
$\lim _{x \to 1} \dfrac{f\left(x\right)-2}{x^{2}-1}=\pi$
$\Rightarrow \dfrac{\lim _{x \to 1}\left(f\left(x\right)-2\right)}{\lim _{x \to 1}\left(x^{2}-1\right)}=\pi$
$\Rightarrow \lim _{x \to 1}\left(f\left(x\right)-2\right)=\pi \lim _{x \to 1}\left(x^{2}-1\right)$
$\Rightarrow \lim _{x \to 1}\left(f\left(x\right)-2\right)=\pi\left(1^{2}-1\right)$
$\Rightarrow \lim _{x \to 1}\left(f\left(x\right)-2\right)=0$
$\Rightarrow \lim _{x \to 1} f\left(x\right)-\lim _{x \to 1} 2=0$
$\Rightarrow \lim _{x \to 1} f\left(x\right)-2=0$
$\therefore \ \ \lim _{x \to 1} f\left(x\right)=2$
32. यदि $f\left(x\right)=\begin{cases} m x^{2}+n, & x<0 \\ \\ n x+m, & 0 \leq x \leq 1 \\ \\ n x^{3}+m, & x>1\end{cases} .$ $m$ और $n$ के किन पूर्णांक मानों के लिए $\lim\limits_{x \to 0} f\left(x\right)$ और $\lim\limits_{x \to 1} f\left(x\right)$ दोनों अस्तित्व में होते हैं?
उत्तर दिखाएं
Answer :
दी गई फलन है
$ \begin{aligned} f\left(x \right) & = \begin{cases}m x^{2}+n, & x<0 \\ \\ n x+m, & 0 \leq x \leq 1 \\ \\ n x^{3}+m, & x>1\end{cases} \\ \\ \lim _{x \to 0^{-}} f\left(x \right) & =\lim _{x \to 0}\left(m x^{2}+n \right) \\ \\ & =m\left(0 \right)^{2}+n \\ \\ & =n \\ \\ \lim _{x \to 0^{+}} f\left(x \right) & =\lim _{x \to 0}\left(n x+m \right) \\ \\ & =n\left(0 \right)+m \\ \\ & =m . \end{aligned} $
इसलिए, $\lim _{x \to 0} f\left(x \right)$ के अस्तित्व के लिए $m=n$ होना आवश्यक है।
$ \begin{aligned} \lim _{x \to 1^{-}} f\left(x \right) & =\lim _{x \to 1}\left(n x+m \right) \\ \\ & =n\left(1 \right)+m \\ \\ & =m+n \end{aligned} $
$\lim _{x \to 1^{+}} f\left(x \right)=\lim _{x \to 1}\left(n x^{3}+m \right)$
$ \hspace{2cm}=n\left(1 \right)^{3}+m $
$ \hspace{2cm}=m+n $
$\therefore \ \ \lim _{x \to 1^{-}} f\left(x \right)=\lim _{x \to 1^{+}} f(x)$
$\qquad\qquad\quad f\left(x \right)=\lim _{x \to 1} f\left(x \right)$
इसलिए, $\lim _{x \to 1} f\left(x \right)$ के अस्तित्व के लिए $m$ और $n$ के किनी भी पूर्णांक मानों के लिए यह अस्तित्व में होता है।
12.5 अवकलज
हमने अनुच्छेद 13.2 में देखा है कि एक वस्तु के विभिन्न समय अंतरालों पर स्थिति के ज्ञान से वस्तु की स्थिति में परिवर्तन की दर ज्ञात की जा सकती है। विभिन्न समय के अंतरालों पर किसी विशिष्ट पैरामीटर के मान के ज्ञान से इसकी परिवर्तन दर के अध्ययन के लिए बहुत व्यापक रूप से रुचि रहती है। ऐसे कई वास्तविक जीवन के स्थितियाँ हैं जहाँ ऐसी प्रक्रिया करनी पड़ती है। उदाहरण के लिए, एक तालाब के बर्तन बनाए रखने वाले लोग जानना चाहते हैं कि तालाब किस समय बर्तन भर जाएगा, जबकि विभिन्न समय बिंदुओं पर पानी की गहराई के ज्ञान के साथ। रॉकेट वैज्ञानिकों को ज्ञात करना पड़ता है कि रॉकेट के विभिन्न समय बिंदुओं पर ऊंचाई के आधार पर उपग्रह को रॉकेट से छोड़ने के लिए किस वेग की आवश्यकता होगी। वित्तीय संस्थानों को ज्ञात करना पड़ता है कि एक विशिष्ट शेयर के मूल्य में परिवर्तन के अध्ययन के लिए इसके वर्तमान मूल्य के आधार पर भविष्यवाणी करनी पड़ती है। इन और कई ऐसे मामलों में एक विशिष्ट पैरामीटर के किसी अन्य पैरामीटर के संबंध में परिवर्तन के अध्ययन की आवश्यकता होती है। विषय का ध्यान एक फलन के क्षेत्र में एक दिए गए बिंदु पर फलन के अवकलज के बारे में है।
परिभाषा 1 मान लीजिए $f$ एक वास्तविक मान फलन है और $a$ इसकी परिभाषा के डोमेन में एक बिंदु है। $f$ के $a$ पर अवकलज को निम्नलिखित द्वारा परिभाषित किया जाता है:
$ \lim\limits_{h \to 0} \dfrac{f(a+h)-f(a)}{h} $
& =\lim\limits_{h \to 0} \dfrac{6+3 h-6}{h}=\lim\limits_{h \to 0} \dfrac{3 h}{h}=\lim\limits_{h \to 0} 3=3 . \end{aligned} $
फलन $3 x$ के $x=2$ पर अवकलज 3 है ।
उदाहरण 6 फलन $f(x)=2 x^{2}+3 x-5$ के $x=-1$ पर अवकलज ज्ञात कीजिए। साथ ही सिद्ध कीजिए कि $f^{\prime}(0)+3 f^{\prime}(-1)=0$ है।
हल हम सबसे पहले $f(x)$ के $x=-1$ और $x=0$ पर अवकलज ज्ञात करते हैं। हमारे पास है
$ \begin{array}{lll} &f^{\prime}(-1) & =\lim\limits_{h \rightarrow 0} \dfrac{f(-1+h)-f(-1)}{h} \\ \\
& {}& =\lim\limits_{h \rightarrow 0} \dfrac{\left[2(-1+h)^{2}+3(-1+h)-5\right]-\left[2(-1)^{2}+3(-1)-5\right]}{h} \\ \\ & {}& =\lim\limits_{h \rightarrow 0} \dfrac{2 h^{2}-h}{h}=\lim\limits_{h \rightarrow 0}(2 h-1)=2(0)-1=-1 \\ \\ \text{and } & f^{\prime}(0) & =\lim\limits_{h \rightarrow 0} \dfrac{f(0+h)-f(0)}{h} \\ \\ & {}& =\lim\limits_{h \rightarrow 0} \dfrac{\left[2(0+h)^{2}+3(0+h)-5\right]-\left[2(0)^{2}+3(0)-5\right]}{h} \\ \\ & {}& =\lim\limits_{h \rightarrow 0} \dfrac{2 h^{2}+3 h}{h}=\lim\limits_{h \rightarrow 0}(2 h+3)=2(0)+3=3
\end{array} $
स्पष्ट रूप से $\quad \quad \quad \quad f^{\prime}(0)+3 f^{\prime}(-1)=0 $
टिप्पणी इस चरण पर ध्यान दें कि बिंदु पर अवकलज के मूल्यांकन में विभिन्न नियमों के प्रभावी उपयोग आवश्यक होता है, सीमा के उपयोग के तहत। नीचे इसका उदाहरण दिया गया है।
उदाहरण 7 $ \sin x $ के अवकलज को $ x=0 $ पर ज्ञात कीजिए।
हल मान लीजिए $ f(x)=\sin x $. तब
$ \begin{aligned} f^{\prime}(0) & =\lim\limits_{h \to 0} \dfrac{f(0+h)-f(0)}{h} \\ & =\lim\limits_{h \to 0} \dfrac{\sin (0+h)-\sin (0)}{h}=\lim\limits_{h \to 0} \dfrac{\sin h}{h}=1
\end{aligned} $
उदाहरण 8 $f(x)=3$ के अवकलज को $x=0$ और $x=3$ पर ज्ञात कीजिए।
हल अवकलज के मापदंड फलन में परिवर्तन को मापता है, इसलिए अनुमान से स्पष्ट है कि स्थिर फलन के अवकलज कोई भी बिंदु पर शून्य होना चाहिए। निम्नलिखित गणना इस बात का समर्थन करती है।
$ f^{\prime}(0)=\lim\limits_{h \to 0} \dfrac{f(0+h)-f(0)}{h}=\lim\limits_{h \to 0} \dfrac{3-3}{h}=\lim\limits_{h \to 0} \dfrac{0}{h}=0 . $
उसी तरह $\quad f^{\prime}(3)=\lim\limits_{h \to 0} \dfrac{f(3+h)-f(3)}{h}=\lim\limits_{h \to 0} \dfrac{3-3}{h}=0$।
अब हम एक फलन के बिंदु पर अवकलज की एक ज्यामितीय व्याख्या प्रस्तुत करते हैं। मान लीजिए $y=f(x)$ एक फलन है जो $f(\boldsymbol{{}a}+\boldsymbol{{}h})$ के रूप में दिया गया है और $P=(a, f(a))$ तथा $Q=(a+h, f(a+h)$ इस फलन के ग्राफ पर एक दूसरे के निकट बिंदु हैं। अब चित्र 12.11 स्वयं स्पष्ट हो गया है।

हम जानते हैं कि $f^{\prime}(a)=\lim\limits_{h \to 0} \dfrac{f(a+h)-f(a)}{h}$
त्रिभुज $PQR$ से स्पष्ट है कि हम लेने वाले अनुपात का सीमा ठीक तौर पर $\tan (QPR)$ के बराबर है, जो चोर्ड $PQ$ की ढलान है। सीमा प्रक्रिया में, जब $h$ 0 के निकट आता है, तो बिंदु $Q$ $P$ के निकट आता है और हम लिख सकते हैं
$ \lim\limits_{h \to 0} \dfrac{f(a+h)-f(a)}{h}=\lim\limits_{Q \to P} \dfrac{QR}{PR} $
यह बात यह भी स्पष्ट है कि चोर्ड $PQ$ वक्र $y=f(x)$ के $P$ पर स्पर्शरेखा के निकट आती है। इसलिए सीमा ठीक तौर पर स्पर्शरेखा की ढलान के बराबर हो जाती है। इसलिए
$
f^{\prime}(a)=\tan \psi $
एक दी गई फ़ंक्शन $f$ के लिए हम प्रत्येक बिंदु पर अवकलज खोज सकते हैं। यदि अवकलज प्रत्येक बिंदु पर मौजूद हो, तो यह एक नई फ़ंक्शन को परिभाषित करता है जिसे $f$ का अवकलज कहते हैं। औपचारिक रूप से, हम एक फ़ंक्शन के अवकलज को निम्नलिखित तरीके से परिभाषित करते हैं।
परिभाषा 2 मान लीजिए $f$ एक वास्तविक मान फ़ंक्शन है, तो निम्नलिखित द्वारा परिभाषित फ़ंक्शन
$ \lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h} $
जहां तक सीमा मौजूद हो, $f$ के $x$ पर अवकलज कहलाता है और $f^{\prime}(x)$ से नोट किया जाता है। इस अवकलज की परिभाषा को अवकलज के प्रथम सिद्धांत के रूप में भी जाना जाता है।
इस प्रकार $ \quad \quad \quad f^{\prime}(x)=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h} $
स्पष्ट रूप से $f^{\prime}(x)$ के प्रांत वहां होता है जहां उपरोक्त सीमा मौजूद होती है। फलन के अवकलज के लिए विभिन्न नोटेशन हो सकते हैं। कभी-कभी $f^{\prime}(x)$ को $\dfrac{d}{d x}(f(x))$ द्वारा दर्शाया जाता है या यदि $y=f(x)$, तो इसे $\dfrac{d y}{d x}$ द्वारा दर्शाया जाता है। इसे $f(x)$ या $y$ के संदर्भ में $x$ के संतत अवकलज के रूप में संदर्भित किया जाता है। इसे अतिरिक्त रूप से $D(f(x))$ द्वारा भी दर्शाया जाता है। इसके अतिरिक्त, $f$ के $x=a$ पर अवकलज को भी $.\dfrac{d}{dx} f(x)\left| _ {a} ~ or .\dfrac{df}{dx}\right| _ {a} $ या तकनीकी रूप से $\left(\dfrac{d f}{d x}\right) _ {x=a}$ द्वारा दर्शाया जाता है।
उदाहरण 9 $f(x)=10 x$ के अवकलज को ज्ञात कीजिए।
हल $f^{\prime}(x)=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$
$ \begin{aligned} & =\lim\limits_{h \to 0} \dfrac{10(x+h)-10(x)}{h} \\ & =\lim\limits_{h \to 0} \dfrac{10 h}{h}=\lim\limits_{h \to 0}(10)=10 . \end{aligned} $
उदाहरण 10 $f(x)=x^{2}$ के अवकलज को ज्ञात कीजिए।
हल हम जानते हैं, $f^{\prime}(x)=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$
$ =\lim\limits_{h \to 0} \dfrac{(x+h)^{2}-(x)^{2}}{h}=\lim\limits_{h \to 0}(h+2 x)=2 x
$
उदाहरण 11 एक नियत फलन $f(x)=a$ के अवकलज को ज्ञात कीजिए, जहाँ $a$ एक निश्चित वास्तविक संख्या है।
हल हम जानते हैं, $f^{\prime}(x)=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$
$ =\lim\limits_{h \to 0} \dfrac{a-a}{h}=\lim\limits_{h \to 0} \dfrac{0}{h}=0 \text{ जब } h \neq 0 $
उदाहरण 12 $f(x)=\dfrac{1}{x}$ के अवकलज को ज्ञात कीजिए
हल हम जानते हैं $f^{\prime}(x)=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$
$ \begin{aligned} & =\lim\limits_{h \to 0} \dfrac{\dfrac{1}{(x+h)}-\dfrac{1}{x}}{h} \\
$$ \begin{aligned} & =\lim\limits_{h \to 0} \dfrac{1}{h}\left[\dfrac{x-(x+h)}{x(x+h)}\right] \\ & =\lim\limits_{h \to 0} \dfrac{1}{h}\left[\dfrac{-h}{x(x+h)}\right] =\lim\limits_{h \to 0} \dfrac{-1}{x(x+h)}=-\dfrac{1}{x^{2}} \end{aligned} $$
12.5.1 कार्यों के अवकलज का बीजगणित
क्योंकि अवकलज की बहुत सी परिभाषा अग्रिम रूप से सीधे सीमा के रूप में दी गई है, हम अवकलज के नियमों को सीमा के नियमों के बराबर अपेक्षित करते हैं। हम इन नियमों को निम्नलिखित प्रमेय में संग्रहित करते हैं।
प्रमेय 5 मान लीजिए $f$ और $g$ दो फलन हैं जिनके अवकलज एक सामान्य डोमेन में परिभाषित हैं। तब
(i) दो फलनों के योग के अवकलज को फलनों के अवकलज के योग के रूप में लिखा जा सकता है।
$ \dfrac{d}{d x}\left[f(x)+g(x)\right]=\dfrac{d}{d x} f(x)+\dfrac{d}{d x} g(x) . $
(ii) दो फलनों के अंतर के अवकलज को फलनों के अवकलज के अंतर के रूप में लिखा जा सकता है।
$ \dfrac{d}{d x}\left[f(x)-g(x)\right]=\dfrac{d}{d x} f(x)-\dfrac{d}{d x} g(x) $
(iii) दो फलनों के गुणनफल के अवकलज को निम्नलिखित गुणन नियम द्वारा दिया जाता है।
$ \dfrac{d}{d x}\left[f(x) \cdot g(x)\right]=\dfrac{d}{d x} f(x) \cdot g(x)+f(x) \cdot \dfrac{d}{d x} g(x)
$
(iv) दो फलनों के भाग के अवकलज को निम्नलिखित भाग नियम द्वारा दिया जाता है (जब नामकरण शून्य न हो)।
$ \dfrac{d}{d x}\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{\dfrac{d}{d x} f(x) \cdot g(x)-f(x) \dfrac{d}{d x} g(x)}{(g(x))^{2}} $
इनके साबित करने के तरीके सीमा के एक समान प्रमेय पर आधारित होते हैं। हम यहां इनके साबित करेंगे। सीमा के मामले में जैसे, इस प्रमेय के अनुसार हम विशेष प्रकार के फलनों के अवकलज की गणना कर सकते हैं। प्रमेय के अंतिम दो कथनों को आसानी से याद रखने के लिए निम्नलिखित रूप में फिर से बयान किया जा सकता है:
Let $u=f(x)$ और $v=g(x)$ हों। तो
$ (u v)^{\prime}=u^{\prime} v+u v^{\prime} $
इसे फ़ंक्शन के उत्पाद के अवकलज के लिए लेब्निज़ नियम कहा जाता है या उत्पाद नियम कहा जाता है। इसी तरह, भाग नियम है
$ \left(\dfrac{u}{v}\right)^{\prime}=\dfrac{u^{\prime} v-u v^{\prime}}{v^{2}} $
अब, कुछ मानक फ़ंक्शन के अवकलज के बारे में बात करते हैं।
यह आसानी से देखा जा सकता है कि फ़ंक्शन $f(x)=x$ का अवकलज नियत फ़ंक्शन 1 है। इसका कारण यह है कि $f^{\prime}(x)=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \dfrac{x+h-x}{h}$
$ =\lim\limits_{h \to 0} 1=1. $
हम इस तथ्य और उपरोक्त प्रमेय का उपयोग करके $f(x)=10 x=x+\ldots .+x$ (दस पद) के अवकलज की गणना करते हैं। उपरोक्त प्रमेय के $(i)$ के अनुसार
$ \begin{aligned} \dfrac{d f(x)}{d x} & =\dfrac{d}{d x}(x+\ldots+x) \quad(\text{ दस पद }) \\ & =\dfrac{d}{d x} x+\ldots+\dfrac{d}{\text{d} x} x \quad(\text{ दस पद }) \\ & =1+\ldots+1 \quad(\text{ दस पद })=10 \end{aligned} $
हम ध्यान रखते हैं कि इस सीमा की गणना उत्पाद नियम का उपयोग करके भी की जा सकती है। लिखें $f(x)=10 x=u v$, जहाँ $u$ एक स्थिर फलन है जो सभी स्थानों पर मान 10 ले रहा है और $v(x)=x$। यहाँ, $f(x)=10 x=u v$ हम जानते हैं कि $u$ के अवकलज के बराबर 0 है। इसके अलावा $v(x)=x$ के अवकलज के बराबर 1 है। इसलिए उत्पाद नियम के अनुसार हम लिख सकते हैं
$ f^{\prime}(x)=(10 x)^{\prime}=(u v)^{\prime}=u^{\prime} v+u v^{\prime}=0 \cdot x+10.1=10 $
उसी तरह, $f(x)=x^{2}$ के अवकलज का मूल्यांकन किया जा सकता है। हम जानते हैं कि $f(x)=x^{2}=x . x$ और इसलिए
$ \begin{aligned} \dfrac{d f}{d x} & =\dfrac{d}{d x}(x \cdot x)=\dfrac{d}{d x}(x) \cdot x+x \cdot \dfrac{d}{d x}(x) \\ & =1 \cdot x+x \cdot 1=2 x . \end{aligned} $
सामान्य रूप से, हम निम्नलिखित प्रमेय के बारे में बता सकते हैं।
प्रमेय 6 $f(x)=x^{n}$ के अवकलज $n x^{n-1}$ होता है, जहाँ $n$ कोई धनात्मक पूर्णांक है।
प्रमाण अवकलज के फलन के परिभाषा के अनुसार, हम निम्नलिखित प्राप्त करते हैं:
$ f^{\prime}(x)=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \dfrac{(x+h)^{n}-x^{n}}{h} . $
द्विपद प्रमेय के अनुसार $(x+h)^{n}=({ }^{n} C_0) x^{n}+({ }^{n} C_1) x^{n-1} h+\ldots+({ }^{n} C_n) h^{n}$ और इसलिए $(x+h)^{n}-x^{n}=h(n x^{n-1}+\ldots+h^{n-1})$. इसलिए
$ \begin{aligned} \dfrac{d f(x)}{d x} & =\lim\limits_{h \to 0} \dfrac{(x+h)^{n}-x^{n}}{h} \\ & =\lim\limits_{h \to 0} \dfrac{h(n x^{n-1}+\ldots .+h^{n-1})}{h} \\
& =\lim\limits_{h \to 0}(n x^{n-1}+\ldots+h^{n-1})=n x^{n-1} . \end{aligned} $
अलग-अलग, हम $n$ पर आगमन और गुणन नियम का उपयोग करके भी इसका सत्यापन कर सकते हैं। $n=1$ के लिए नतीजा सही है, जिसे पहले से सिद्ध कर लिया गया है। हम लेते हैं
$ \begin{aligned} \dfrac{d}{d x}\left(x^{n}\right) & =\dfrac{d}{d x}\left(x \cdot x^{n-1}\right) \\ & =\dfrac{d}{d x}(x) \cdot\left(x^{n-1}\right)+x \cdot \dfrac{d}{d x}\left(x^{n-1}\right) \text{ (गुणन नियम के अनुसार) } \\ & =1 \cdot x^{n-1}+x \cdot\left((n-1) x^{n-2}\right) \text{ (आगमन अनुमान के अनुसार) } \\
& =x^{n-1}+(n-1) x^{n-1}=n x^{n-1} . \end{aligned} $
Remark उपरोक्त प्रमेय $x$ के सभी घातों के लिए सत्य है, अर्थात $n$ कोई भी वास्तविक संख्या हो सकती है (लेकिन हम यहां सिद्ध नहीं करेंगे)।
12.5.2 बहुपद एवं त्रिकोणमितीय फलनों के अवकलज
हम एक ऐसे प्रमेय से शुरू करते हैं जो हमें बहुपदीय फलन के अवकलज के बारे में बताता है।
प्रमेय 7 मान लीजिए $f(x)=a_n x^{n}+a _{n-1} x^{n-1}+\ldots .+a_1 x+a_0$ एक बहुपदीय फलन है, जहां $a_i s$ सभी वास्तविक संख्याएं हैं और $a_n \neq 0$ है। तब, अवकलज फलन निम्नलिखित द्वारा दिया जाता है
$ \dfrac{d f(x)}{d x}=n a_n x^{n-1}+(n-1) a _{n-1} x^{x-2}+\ldots+2 a_2 x+a_1 $
इस प्रमेय के साबित करना केवल प्रमेय 5 के भाग (i) और प्रमेय 6 को मिलाकर किया जाता है।
उदाहरण 13 $6 x^{100}-x^{55}+x$ का अवकलज निकालें।
हल ऊपर के प्रमेय के सीधे अनुप्रयोग से यह दिखाई देता है कि ऊपर दी गई फ़ंक्शन का अवकलज $600 x^{99}-55 x^{54}+1$ है।
उदाहरण 14 $f(x)=1+x+x^{2}+x^{3}+\ldots+x^{50}$ के अवकलज को $x=1$ पर निकालें।
हल ऊपर के प्रमेय 6 के सीधे अनुप्रयोग से यह दिखाई देता है कि ऊपर दी गई फ़ंक्शन का अवकलज $1+2 x+3 x^{2}+\ldots+50 x^{49}$ है। $x=1$ पर इस फ़ंक्शन का मान $1+2(1)+3(1)^{2}+\ldots+50(1)^{49}=1+2+3+\ldots+50=\dfrac{(50)(51)}{2}=1275$ है।
उदाहरण 15 $f(x)=\dfrac{x+1}{x}$ के अवकलज की गणना कीजिए।
हल स्पष्ट रूप से यह फलन $x=0$ के अतिरिक्त सभी बिंदुओं पर परिभाषित है। हम $u=x+1$ और $v=x$ के साथ भाग नियम का उपयोग करते हैं। इसलिए $u^{\prime}=1$ और $v^{\prime}=1$ है। अतः
$ \dfrac{d f(x)}{d x}=\dfrac{d}{d x}\left(\dfrac{x+1}{x}\right)=\dfrac{d}{d x}\left(\dfrac{u}{v}\right)=\dfrac{u^{\prime} v-u v^{\prime}}{v^{2}}=\dfrac{1(x)-(x+1) 1}{x^{2}}=-\dfrac{1}{x^{2}} $
उदाहरण 16 $\sin x$ का अवकलज निकालिए।
हल मान लीजिए $f(x)=\sin x$। तब
$ \begin{aligned} \dfrac{d f(x)}{d x} & =\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \dfrac{\sin (x+h)-\sin (x)}{h} \\ & =\lim\limits_{h \to 0} \dfrac{2 \cos \left(\dfrac{2 x+h}{2}\right) \sin \left(\dfrac{h}{2}\right)}{h} \text{ (using formula for sin A - sin B) } \\ & =\lim\limits_{h \to 0} \cos \left(x+\dfrac{h}{2}\right) \cdot \lim\limits_{h \to 0} \dfrac{\sin \dfrac{h}{2}}{\dfrac{h}{2}}=\cos x \cdot 1=\cos x . \end{aligned} $
उदाहरण 17 $\tan x$ का अवकलज निकालें।
हल मान लीजिए $f(x)=\tan x$. तो
$ \begin{aligned} \dfrac{d f(x)}{d x} & =\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \dfrac{\tan (x+h)-\tan (x)}{h} \\ & =\lim\limits_{h \to 0} \dfrac{1}{h}\left[\dfrac{\sin (x+h)}{\cos (x+h)}-\dfrac{\sin x}{\cos x}\right] \\ & =\lim\limits_{h \to 0}\left[\dfrac{\sin (x+h) \cos x-\cos (x+h) \sin x}{h \cos (x+h) \cos x}\right] \\ & .=\lim\limits_{h \to 0} \dfrac{\sin (x+h-x)}{h \cos (x+h) \cos x} \text{ (सूत्र का उपयोग करते हुए } \sin (A+B)) \\
$$ \begin{aligned} & =\lim\limits_{h \to 0} \dfrac{\sin h}{h} \cdot \lim\limits_{h \to 0} \dfrac{1}{\cos (x+h) \cos x} \\ & =1 \cdot \dfrac{1}{\cos ^{2} x}=\sec ^{2} x . \end{aligned} $$
उदाहरण 18 $f(x)=\sin ^{2} x$ के अवकलज की गणना कीजिए।
हल हम लेब्निज गुणन नियम का उपयोग करके इसकी गणना करते हैं।
$$ \begin{aligned} \dfrac{d f(x)}{d x} & =\dfrac{d}{d x}(\sin x \sin x) \\ & =(\sin x)^{\prime} \sin x+\sin x(\sin x)^{\prime} \\ & =(\cos x) \sin x+\sin x(\cos x) \\ & =2 \sin x \cos x=\sin 2 x . \end{aligned} $$
$
अभ्यास 12.2
1. $x^{2}-2$ का $x=10$ पर अवकलज ज्ञात कीजिए।
उत्तर दिखाएँ
उत्तर :
मान लीजिए $f\left(x \right)=x^{2} - 2$. अतः,
$ \begin{aligned} f^{\prime}\left(10 \right) & =\lim _ {h \rightarrow 0} \dfrac{f\left(10+h \right)-f\left(10 \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{\left[\left(10+h \right)^{2}-2\right]-\left(10^{2}-2 \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{10^{2}+2 \cdot 10 \cdot h+h^{2}-2-10^{2}+2}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{20 h+h^{2}}{h} \\ \\ & =\lim _ {h \rightarrow 0}\left(20+h \right)=\left(20+0 \right)=20 \end{aligned} $
अतः, $x^{2} - 2$ का $x=10$ पर अवकलज $20$ है।
2. $x$ का $x=1$ पर अवकलज ज्ञात कीजिए।
उत्तर दिखाएँ
उत्तर :
मान लीजिए, $ \ f\left(x \right)=x$. अतः,
$ \ \ \ \ \begin{aligned} f^{\prime}\left(1 \right) & =\lim _ {h \rightarrow 0} \dfrac{f\left(1+h \right)-f\left(1 \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{\left(1+h \right)-1}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{h}{h} \\ \\ & =\lim _ {h \rightarrow 0}\left(1 \right) \\ \\ & =1 \end{aligned} $
अतः, $x$ का $x=1$ पर अवकलज $1$ है।
3. $99 x$ का $x=100$ पर अवकलज ज्ञात कीजिए।
उत्तर दिखाएँ
उत्तर :
मान लीजिए $f\left(x \right)=99 x \quad$ अतः,
$ \begin{aligned} f^{\prime}\left(100 \right) & =\lim _ {h \rightarrow 0} \dfrac{f\left(100+h \right)-f\left(100 \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{99\left(100+h \right)-99\left(100 \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{99 \times 100+99 h-99 \times 100}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{99 h}{h} \\ \\ & =\lim _ {h \rightarrow 0}\left(99 \right)=99 \end{aligned} $
अतः, $99 x$ का $x=100$ पर अवकलज $99$ है।
4. निम्नलिखित फलनों के अवकलज पहले सिद्धांत से ज्ञात कीजिए।
(i) $x^{3}-27$
(ii) $\left(x-1 \right)\left(x-2 \right)$
(iii) $\dfrac{1}{x^{2}}$
(iv) $\dfrac{x+1}{x-1}$
उत्तर दिखाएँ
उत्तर :
(i) मान लीजिए $f\left(x \right)=x^{3} - 27$
अतः पहले सिद्धांत से,
$ \begin{aligned} f^{\prime}\left(x \right) & =\lim _ {h \rightarrow 0} \dfrac{f\left(x+h \right)-f\left(x \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{\left[\left(x+h \right)^{3}-27\right]-\left(x^{3}-27 \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{x^{3}+h^{3}+3 x^{2} h+3 x h^{2}-x^{3}}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{h^{3}+3 x^{2} h+3 x h^{2}}{h} \\ \\ & =\lim _ {h \rightarrow 0}\left(h^{2}+3 x^{2}+3 x h \right) \\ \\ & =0+3 x^{2}+0=3 x^{2} \end{aligned} $
(ii) मान लीजिए, $ \ f\left(x \right)=\left(x- 1 \right)\left(x - 2 \right)\quad$
अतः पहले सिद्धांत से,
$ \ f^{\prime}\left(x \right)=\lim _ {h \rightarrow 0} \dfrac{f\left(x+h \right)-f\left(x \right)}{h} $
$\qquad\quad =\lim _ {h \rightarrow 0} \dfrac{\left(x+h-1 \right)\left(x+h-2 \right)-\left(x-1 \right)\left(x-2 \right)}{h} $
$\qquad\quad =\lim _ {h \rightarrow 0} \dfrac{\left(x^{2}+h x-2 x+h x+h^{2}-2 h-x-h+2 \right)-\left(x^{2}-2 x-x+2 \right)}{h} $
$\qquad\quad =\lim _ {h \rightarrow 0} \dfrac{\left(h x+h x+h^{2}-2 h-h \right)}{h} $
$\qquad\quad =\lim _ {h \rightarrow 0} \dfrac{2 h x+h^{2}-3 h}{h} $
$\qquad\quad =\lim _ {h \rightarrow 0}\left(2 x+h-3 \right) $
$\qquad\quad=\left(2 x+0-3 \right) $
$\qquad\quad =2 x-3 $
(iii) मान लीजिए $f\left(x \right)=\dfrac{1}{x^{2}}$
अतः पहले सिद्धांत से,
$f^{\prime}\left(x \right)=\lim _ {h \rightarrow 0} \dfrac{f\left(x+h \right)-f\left(x \right)}{h}$
$\hspace{1cm} =\lim _ {h \rightarrow 0} \dfrac{\dfrac{1}{\left(x+h \right)^{2}}-\dfrac{1}{x^{2}}}{h} $
$\hspace{1cm} =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{x^{2}-\left(x+h \right)^{2}}{x^{2}\left(x+h \right)^{2}}\right] $
$\hspace{1cm} =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{x^{2}-x^{2}-h^{2}-2 h x}{x^{2}\left(x+h \right)^{2}}\right] $
$\hspace{1cm} =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{-h^{2}-2 h x}{x^{2}\left(x+h \right)^{2}}\right] $
$\hspace{1cm} =\lim _ {h \rightarrow 0}\left[\dfrac{-h-2 x}{x^{2}\left(x+h \right)^{2}}\right] $
$\hspace{1cm} =\dfrac{0-2 x}{x^{2}\left(x+0 \right)^{2}}=\dfrac{-2}{x^{3}} $
$\hspace{0.2cm} f\left(x \right)=\dfrac{x+1}{x-1}$
$ \text{ (iv) Let } f(x)=\dfrac{x+1}{x-1}\quad$
$ \text{ Accordingly, from the first principle, }$
$ \begin{aligned} f^{\prime}\left(x \right) & =\lim _ {h \rightarrow 0} \dfrac{f\left(x+h \right)-f\left(x \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{\left(\dfrac{x+h+1}{x+h-1}-\dfrac{x+1}{x-1} \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\left(x-1 \right)\left(x+h+1 \right)-\left(x+1 \right)\left(x+h-1 \right)}{\left(x-1 \right)\left(x+h-1 \right)}\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\left(x^{2}+h x+x-x-h-1 \right)-\left(x^{2}+h x-x+x+h-1 \right)}{\left(x-1 \right)\left(x+h-1 \right)}\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{-2 h}{\left(x-1 \right)\left(x+h-1 \right)}\right] \\ \\ & =\lim _ {h \rightarrow 0}\left[\dfrac{-2}{\left(x-1 \right)\left(x+h-1 \right)}\right] \\ \\ & =\dfrac{-2}{\left(x-1 \right)\left(x-1 \right)}=\dfrac{-2}{\left(x-1 \right)^{2}} \end{aligned} $
5. फलन के लिए
$ f\left(x \right)=\dfrac{x^{100}}{100}+\dfrac{x^{99}}{99}+\ldots+\dfrac{x^{2}}{2}+x+1 . $
सिद्ध करें कि $f^{\prime}\left(1 \right)=100 f^{\prime}\left(0 \right)$.
उत्तर दिखाएं
Answer :
दिया गया फलन है $f\left(x \right)=\dfrac{x^{100}}{100}+\dfrac{x^{99}}{99}+\ldots+\dfrac{x^{2}}{2}+x+1$
$\dfrac{d}{d x} f\left(x \right)=\dfrac{d}{d x}\left[\dfrac{x^{100}}{100}+\dfrac{x^{99}}{99}+\ldots+\dfrac{x^{2}}{2}+x+1\right]$
$\dfrac{d}{d x} f\left(x \right)=\dfrac{d}{d x}\left(\dfrac{x^{100}}{100} \right)+\dfrac{d}{d x}\left(\dfrac{x^{99}}{99} \right)+\ldots+\dfrac{d}{d x}\left(\dfrac{x^{2}}{2} \right)+\dfrac{d}{d x}\left(x \right)+\dfrac{d}{d x}\left(1 \right)$
उपयोग करते हुए प्रमेय $\dfrac{d}{d x}\left(x^{n} \right)=n x^{n-1}$, हम प्राप्त करते हैं
$\dfrac{d}{d x} f\left(x \right)=\dfrac{100 x^{99}}{100}+\dfrac{99 x^{98}}{99}+\ldots+\dfrac{2 x}{2}+1+0$
$ \qquad \qquad =x^{99}+x^{98}+\ldots+x+1 $
$\therefore f^{\prime}\left(x \right)=x^{99}+x^{98}+\ldots+x+1$
$ x=0 $ पर,
$ f^{\prime}\left(0 \right)=1 $
$ x=1 $ पर,
$ f^{\prime}\left(1 \right)=1^{99}+1^{98}+\ldots+1+1=\left[1+1+\ldots+1+1\right] _ {\text{पदों के लिए}}=1 \times 100=100 $
इसलिए, $ f^{\prime}\left(1 \right)=100 \times f^{1}\left(0 \right) $
6. कुछ निश्चित वास्तविक संख्या $ a $ के लिए $ x^{n}+a x^{n-1}+a^{2} x^{n-2}+\ldots+a^{n-1} x+a^{n} $ का अवकलज ज्ञात कीजिए।
उत्तर दिखाएं
उत्तर :
मान लीजिए $ f\left(x \right)=x^{n}+a x^{n-1}+a^{2} x^{n-2}+\ldots+a^{n-1} x+a^{n} $
$\therefore f^{\prime}\left(x \right)=\dfrac{d}{d x}\left(x^{n}+a x^{n-1}+a^{2} x^{n-2}+\ldots+a^{n-1} x+a^{n} \right)$
$\hspace{1.3cm}=\dfrac{d}{d x}\left(x^{n} \right)+a \dfrac{d}{d x}\left(x^{n-1} \right)+a^{2} \dfrac{d}{d x}\left(x^{n-2} \right)+\ldots+a^{n-1} \dfrac{d}{d x}\left(x \right)+a^{n} \dfrac{d}{d x}\left(1 \right)$
प्रमेय $\dfrac{d}{d x} x^{n}=n x^{n-1}$ का उपयोग करते हुए, हम प्राप्त करते हैं
$ \begin{aligned} f^{\prime}\left(x \right) & =n x^{n-1}+a\left(n-1 \right) x^{n-2}+a^{2}\left(n-2 \right) x^{n-3}+\ldots+a^{n-1}+a^{n}\left(0 \right) \\ \\ & =n x^{n-1}+a\left(n-1 \right) x^{n-2}+a^{2}\left(n-2 \right) x^{n-3}+\ldots+a^{n-1} \end{aligned} $
7. कुछ नियतांक $ a $ और $ b $ के लिए निम्नलिखित के अवकलज ज्ञात कीजिए
(i) $\left(x-a \right)\left(x-b \right)$
(ii) $\left(a x^{2}+b \right)^{2}$
(iii) $\dfrac{x-a}{x-b}$
उत्तर दिखाएं
उत्तर :
(i) मान लीजिए $ f\left(x \right)=\left(x - a \right) \left(x - b \right) $
$ \begin{aligned} \Rightarrow f\left(x \right) & =x^{2}-\left(a+b \right) x+a b \\ \\ \therefore f^{\prime}\left(x \right) & =\dfrac{d}{d x}\left(x^{2}-\left(a+b \right) x+a b \right) \\ \\ & =\dfrac{d}{d x}\left(x^{2} \right)-\left(a+b \right) \dfrac{d}{d x}\left(x \right)+\dfrac{d}{d x}\left(a b \right) `
\end{aligned} $
उपयोग करते हुए प्रमेय $\dfrac{d}{d x}\left(x^{n} \right)=n x^{n-1}$, हम प्राप्त करते हैं
$f^{\prime}\left(x \right)=2 x-\left(a+b \right)+0=2 x-a-b$
(ii) मान लीजिए $f\left(x \right)=\left(a x^{2}+b \right)^{2}$
$\Rightarrow f\left(x \right)=a^{2} x^{4}+2 a b x^{2}+b^{2}$
$\therefore f^{\prime}\left(x \right)=\dfrac{d}{d x}\left(a^{2} x^{4}+2 a b x^{2}+b^{2} \right)=a^{2} \dfrac{d}{d x}\left(x^{4} \right)+2 a b \dfrac{d}{d x}\left(x^{2} \right)+\dfrac{d}{d x}\left(b^{2} \right)$
उपयोग करते हुए प्रमेय $\dfrac{d}{d x} x^{n}=n x^{n-1}$, हम प्राप्त करते हैं
$ \begin{aligned} f^{\prime}\left(x \right) & =a^{2}\left(4 x^{3} \right)+2 a b\left(2 x \right)+b^{2}\left(0 \right) \\ \\ & =4 a^{2} x^{3}+4 a b x \\ \\ & =4 a x\left(a x^{2}+b \right) \end{aligned} $
(iii)
मान लीजिए $f\left(x \right)=\dfrac{\left(x-a \right)}{\left(x-b \right)}$
$\Rightarrow f^{\prime}\left(x \right)=\dfrac{d}{d x}\left(\dfrac{x-a}{x-b} \right)$
भाग नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x \right) & =\dfrac{\left(x-b \right) \dfrac{d}{d x}\left(x-a \right)-\left(x-a \right) \dfrac{d}{d x}\left(x-b \right)}{\left(x-b \right)^{2}} \\ \\ & =\dfrac{\left(x-b \right)\left(1 \right)-\left(x-a \right)\left(1 \right)}{\left(x-b \right)^{2}} \\ \\ & =\dfrac{x-b-x+a}{\left(x-b \right)^{2}} \\ \\ & =\dfrac{a-b}{\left(x-b \right)^{2}} \end{aligned} $
8. कुछ अचर $a$ के लिए $\dfrac{x^{n}-a^{n}}{x-a}$ का अवकलज ज्ञात कीजिए।
उत्तर दिखाएँ
उत्तर :
मान लीजिए $f\left(x \right)=\dfrac{x^{n}-a^{n}}{x-a}$
$\Rightarrow f^{\prime}\left(x \right)=\dfrac{d}{d x}\left(\dfrac{x^{n}-a^{n}}{x-a} \right)$
भाग नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x \right) & =\dfrac{\left(x-a \right) \dfrac{d}{d x}\left(x^{n}-a^{n} \right)-\left(x^{n}-a^{n} \right) \dfrac{d}{d x}\left(x-a \right)}{\left(x-a \right)^{2}} \\ \\ & =\dfrac{\left(x-a \right)\left(n x^{n-1}-0 \right)-\left(x^{n}-a^{n} \right)}{\left(x-a \right)^{2}} \\ \\ & =\dfrac{n x^{n}-a n x^{n-1}-x^{n}+a^{n}}{\left(x-a \right)^{2}}
\end{aligned} $
9. निम्नलिखित का अवकलज ज्ञात कीजिए
(i) $2 x-\dfrac{3}{4}$
(ii) $\left(5 x^{3}+3 x-1 \right)\left(x-1 \right)$
(iii) $x^{-3}\left(5+3 x \right)$
(iv) $x^{5}\left(3-6 x^{-9} \right)$
(v) $x^{-4}\left(3-4 x^{-5} \right)$
(vi) $\dfrac{2}{x+1}-\dfrac{x^{2}}{3 x-1}$
उत्तर दिखाएं
Answer :
(i) मान लीजिए $f\left(x \right)=2 x-\dfrac{3}{4}$
$ \begin{aligned} f^{\prime}\left(x \right) & =\dfrac{d}{d x}\left(2 x-\dfrac{3}{4} \right) \\ \\ & =2 \dfrac{d}{d x}\left(x \right)-\dfrac{d}{d x}\left(\dfrac{3}{4} \right) \\ \\ & =2-0 \\ \\ & =2 \end{aligned} $
(ii) मान लीजिए $f\left(x \right)=\left(5 x^{3}+3 x - 1 \right)\left(x- 1 \right)$
Leibnitz गुणन नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x \right) & =\left(5 x^{3}+3 x-1 \right) \dfrac{d}{d x}\left(x-1 \right)+\left(x-1 \right) \dfrac{d}{d x}\left(5 x^{3}+3 x-1 \right) \\ \\ & =\left(5 x^{3}+3 x-1 \right)\left(1 \right)+\left(x-1 \right)\left(5.3 x^{2}+3-0 \right) \\ \\ & =\left(5 x^{3}+3 x-1 \right)+\left(x-1 \right)\left(15 x^{2}+3 \right) \\ \\ & =5 x^{3}+3 x-1+15 x^{3}+3 x-15 x^{2}-3 \\ \\ & =20 x^{3}-15 x^{2}+6 x-4 \end{aligned} $
(iii) मान लीजिए $f \left(x \right)=x^{-3}\left(5+3 x \right)$
Leibnitz गुणन नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x \right) & =x^{-3} \dfrac{d}{d x}\left(5+3 x \right)+\left(5+3 x \right) \dfrac{d}{d x}\left(x^{-3} \right) \\ \\ & =x^{-3}\left(0+3 \right)+\left(5+3 x \right)\left(-3 x^{-3-1} \right) \\ \\ & =x^{-3}\left(3 \right)+\left(5+3 x \right)\left(-3 x^{-4} \right) \\ \\ & =3 x^{-3}-15 x^{-4}-9 x^{-3} \\ \\ & =-6 x^{-3}-15 x^{-4} \\ \\ & =-3 x^{-3}\left(2+\dfrac{5}{x} \right) \\ \\ & =\dfrac{-3 x^{-3}}{x}\left(2 x+5 \right) \\ \\ & =\dfrac{-3}{x^{4}}\left(5+2 x \right) \end{aligned} $
(iv) मान लीजिए $f\left(x \right)=x^{5}\left(3 - 6 x^{- 9} \right)$
Leibnitz गुणन नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x \right) & =x^{5} \dfrac{d}{d x}\left(3-6 x^{-9} \right)+\left(3-6 x^{-9} \right) \dfrac{d}{d x}\left(x^{5} \right) \\ \\
& =x^{5} \lbrace 0-6\left(-9 \right) x^{-9-1} \rbrace +\left(3-6 x^{-9} \right)\left(5 x^{4} \right) \\ \\ & =x^{5}\left(54 x^{-10} \right)+15 x^{4}-30 x^{-5} \\ \\ & =54 x^{-5}+15 x^{4}-30 x^{-5} \\ \\ & =24 x^{-5}+15 x^{4} \\ \\ & =15 x^{4}+\dfrac{24}{x^{5}} \end{aligned} $
(v) अगर $f\left(x \right)=x^{- 4}\left(3 - 4 x ^{-5} \right)$
Leibnitz गुणन नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x \right) & =x^{-4} \dfrac{d}{d x}\left(3-4 x^{-5} \right)+\left(3-4 x^{-5} \right) \dfrac{d}{d x}\left(x^{-4} \right) \\ \\ & =x^{-4} \lbrace 0-4\left(-5 \right) x^{-5-1} \rbrace +\left(3-4 x^{-5} \right)\left(-4 \right) x^{-4-1} \\ \\ & =x^{-4}\left(20 x^{-6} \right)+\left(3-4 x^{-5} \right)\left(-4 x^{-5} \right) \\ \\ & =20 x^{-10}-12 x^{-5}+16 x^{-10} \\ \\ & =36 x^{-10}-12 x^{-5} \\ \\ & =-\dfrac{12}{x^{5}}+\dfrac{36}{x^{10}} \end{aligned} $
(vi) $ \ \ \dfrac{2}{x+1}-\dfrac{x^2}{3x-1} $
$f^{\prime}\left(x \right)=\dfrac{d}{d x}\left(\dfrac{2}{x+1} \right)-\dfrac{d}{d x}\left(\dfrac{x^{2}}{3 x-1} \right)$
भाग नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x \right) & =\left[\dfrac{\left(x+1 \right) \dfrac{d}{d x}\left(2 \right)-2 \dfrac{d}{d x}\left(x+1 \right)}{\left(x+1 \right)^{2}}\right]-\left[\dfrac{\left(3 x-1 \right) \dfrac{d}{d x}\left(x^{2} \right)-x^{2} \dfrac{d}{d x}\left(3 x-1 \right)}{\left(3 x-1 \right)^{2}}\right] \\ \\ & =\left[\dfrac{\left(x+1 \right)\left(0 \right)-2\left(1 \right)}{\left(x+1 \right)^{2}}\right]-\left[\dfrac{\left(3 x-1 \right)\left(2 x \right)-\left(x^{2} \right)\left(3 \right)}{\left(3 x-1 \right)^{2}}\right] \\ \\ & =\dfrac{-2}{\left(x+1 \right)^{2}}-\left[\dfrac{6 x^{2}-2 x-3 x^{2}}{\left(3 x-1 \right)^{2}}\right] \\ \\ & =\dfrac{-2}{\left(x+1 \right)^{2}}-\left[\dfrac{3 x^{2}-2 x}{\left(3 x-1 \right)^{2}}\right] \\ \\ & =\dfrac{-2}{\left(x+1 \right)^{2}}-\dfrac{x\left(3 x-2 \right)}{\left(3 x-1 \right)^{2}} \end{aligned} $
10. पहले सिद्धांत से $\cos x$ का अवकलज ज्ञात कीजिए।
उत्तर दिखाएं
उत्तर :
मान लीजिए $f\left(x \right)=\cos x$.
इसलिए, पहले सिद्धांत से,
$ \begin{aligned} f^{\prime}\left(x \right) & =\lim _ {h \rightarrow 0} \dfrac{f\left(x+h \right)-f\left(x \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{\cos \left(x+h \right)-\cos x}{h} \\ \\ & =\lim _ {h \rightarrow 0}\left[\dfrac{\cos x \cos h-\sin x \sin h-\cos x}{h}\right] \\ \\ & =\lim _ {h \rightarrow 0}\left[\dfrac{-\cos x\left(1-\cos h \right)-\sin x \sin h}{h}\right] \\ \\ & =\lim _ {h \rightarrow 0}\left[\dfrac{-\cos x\left(1-\cos h \right)}{h}-\dfrac{\sin x \sin h}{h}\right] \\ \\ & =-\cos x\left(\lim _ {h \rightarrow 0} \dfrac{1-\cos h}{h} \right)-\sin x \lim _ {h \rightarrow 0}\left(\dfrac{\sin h}{h} \right) \\ \\ & =-\cos x\left(0 \right)-\sin x\left(1 \right) \\ \\ & =-\sin x \\ \\ \therefore \ \ f^{\prime}\left(x \right) & =-\sin x \end{aligned} $
11. निम्नलिखित फलनों के अवकलज ज्ञात कीजिए:
(i) $\sin x \cos x$
(ii) $\sec x$
(iii) $5 \sec x+4 \cos x$
(iv) $\text{cosec} \ x$
(v) $3 \cot x+5 \text{cosec} \ x$
(vi) $5 \sin x-6 \cos x+7$
(vii) $2 \tan x-7 \sec x$
उत्तर दिखाएं
उत्तर :
(i) मान लीजिए $f\left(x \right)=\sin x \cos x$.
इसलिए, पहले सिद्धांत से,
$ \begin{aligned} f^{\prime}\left(x \right) & =\lim _ {h \rightarrow 0} \dfrac{f\left(x+h \right)-f\left(x \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{\sin \left(x+h \right) \cos \left(x+h \right)-\sin x \cos x}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{2 h}\left[2 \sin \left(x+h \right) \cos \left(x+h \right)-2 \sin x \cos x\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{2 h}\left[\sin 2\left(x+h \right)-\sin 2 x\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{2 h}\left[2 \cos \dfrac{2 x+2 h+2 x}{2} \cdot \sin \dfrac{2 x+2 h-2 x}{2}\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\cos \dfrac{4 x+2 h}{2} \sin \dfrac{2 h}{2}\right] \\ \\
& =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\cos \left(2 x+h \right) \sin h\right] \\ \\ & =\lim _ {h \rightarrow 0} \cos \left(2 x+h \right) \cdot \lim _ {h \rightarrow 0} \dfrac{\sin h}{h} \\ \\ & =\cos \left(2 x+0 \right) \cdot 1 \\ \\ & =\cos 2 x \end{aligned} $
(ii) मान लीजिए $f \left(x \right)=\sec x$.
इस प्रकार, पहले सिद्धांत से,
$ \begin{aligned} f^{\prime}\left(x \right) & =\lim _ {h \rightarrow 0} \dfrac{f\left(x+h \right)-f\left(x \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{\sec \left(x+h \right)-\sec x}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{1}{\cos \left(x+h \right)}-\dfrac{1}{\cos x}\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\cos x-\cos \left(x+h \right)}{\cos x \cos \left(x+h \right)}\right] \\ \\ & =\dfrac{1}{\cos x} \cdot \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{-2 \sin \left(\dfrac{x+x+h}{2} \right) \sin \left(\dfrac{x-x-h}{2} \right)}{\cos \left(x+h \right)}\right] \\ \\ & =\dfrac{1}{\cos x} \cdot \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{-2 \sin \left(\dfrac{2 x+h}{2} \right) \sin \left(-\dfrac{h}{2} \right)}{\cos \left(x+h \right)}\right] \\ \\ & =\dfrac{1}{\cos x} \lim _ {h \rightarrow 0} \dfrac{\left[\sin \left(\dfrac{2 x+h}{2} \right) \dfrac{\sin \left(\dfrac{h}{2} \right)}{\left(\dfrac{h}{2} \right)}\right]}{\cos \left(x+h \right)} \\ \\ & =\dfrac{1}{\cos x} \cdot \lim _ {\frac{h}{2} \rightarrow 0} \dfrac{\sin \left(\dfrac{h}{2} \right)}{\left(\dfrac{h}{2} \right)} \cdot \lim _ {h \rightarrow 0} \dfrac{\sin \left(\dfrac{2 x+h}{2} \right)}{\cos \left(x+h \right)} \\ \\ & =\dfrac{1}{\cos x} \cdot 1 \dfrac{\sin x}{\cos x} \\ \\ & =\sec x \tan x \end{aligned} $
(iii) मान लीजिए $f \left(x \right)=5 \sec x+4 \cos x$.
इस प्रकार, पहले सिद्धांत से,
$ \begin{aligned} f^{\prime}\left(x \right) & =\lim _ {h \rightarrow 0} \dfrac{f\left(x+h \right)-f\left(x \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{5 \sec \left(x+h \right)+4 \cos \left(x+h \right)-\left[5 \sec x+4 \cos x\right]}{h} \\ \\
& =5 \lim _ {h \rightarrow 0} \dfrac{\left[\sec \left(x+h \right)-\sec x\right]}{h}+4 \lim _ {h \rightarrow 0} \dfrac{\left[\cos \left(x+h \right)-\cos x\right]}{h} \\ \\ & =5 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{1}{\cos \left(x+h \right)}-\dfrac{1}{\cos x}\right]+4 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\cos \left(x+h \right)-\cos x\right] \\ \\ & =5 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\cos x-\cos \left(x+h \right)}{\cos x \cos \left(x+h \right)}\right]+4 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\cos x \cos h-\sin x \sin h-\cos x\right] \\ \\ & =\dfrac{5}{\cos x} \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{-2 \sin \left(\dfrac{x+x+h}{2} \right) \sin \left(\dfrac{x-x-h}{2} \right)}{\cos \left(x+h \right)}\right]+4 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[-\cos x\left(1-\cos h \right)-\sin x \sin h\right] \\ \\ & =\dfrac{5}{\cos x} \cdot \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{-2 \sin \left(\dfrac{2 x+h}{2} \right) \sin \left(-\dfrac{h}{2} \right)}{\cos \left(x+h \right)}\right]+4\left[-\cos x \lim _ {h \rightarrow 0} \dfrac{\left(1-\cos h \right)}{h}-\sin x \lim _ {h \rightarrow 0} \dfrac{\sin h}{h}\right] \\ \\ & =\dfrac{5}{\cos x} \cdot \lim _ {h \rightarrow 0}\left[\dfrac{\sin \left(\dfrac{2 x+h}{2} \right) \cdot \dfrac{\sin \left(\dfrac{h}{2} \right)}{\dfrac{h}{2}}}{\cos \left(x+h \right)}\right]+4\left[\left(-\cos x \right) \cdot\left(0 \right)-\left(\sin x \right) \cdot 1\right] \\ \\ & =\dfrac{5}{\cos x} \cdot\left[\lim _ {h \rightarrow 0} \dfrac{\sin \left(\dfrac{2 x+h}{2} \right)}{\cos \left(x+h \right)} \cdot \lim _ {h \rightarrow 0} \dfrac{\sin \left(\dfrac{h}{2} \right)}{\dfrac{h}{2}}\right]-4 \sin x \\ \\ & =\dfrac{5}{\cos x} \cdot \dfrac{\sin x}{\cos x} \cdot 1-4 \sin x \\ \\ & =5 \sec x \tan x \cdot-4 \sin x \end{aligned} $
(iv) अब $f\left(x \right)=\text{cosec } x$.
इसलिए, पहले सिद्धांत से,
$ \begin{aligned} f^{\prime}\left(x \right) & =\lim _ {h \rightarrow 0} \dfrac{f\left(x+h \right)-f\left(x \right)}{h} \\ \\
$$ \begin{aligned} f^{\prime}\left(x \right) & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[cosec \ \left(x+h \right)-cosec \ x\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{1}{\sin \left(x+h \right)}-\dfrac{1}{\sin x}\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\sin x-\sin \left(x+h \right)}{\sin \left(x+h \right) \sin x}\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{2 \cos \left(\dfrac{x+x+h}{2} \right) \cdot \sin \left(\dfrac{x-x-h}{2} \right)}{\sin \left(x+h \right) \sin x}\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{2 \cos \left(\dfrac{2 x+h}{2} \right) \sin \left(-\dfrac{h}{2} \right)}{\sin \left(x+h \right) \sin x}\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{-\cos \left(\dfrac{2 x+h}{2} \right) \cdot \dfrac{\sin \left(\dfrac{h}{2} \right)}{\left(\dfrac{h}{2} \right)}}{\sin \left(x+h \right) \sin x} \\ \\ & =\lim _ {h \rightarrow 0}\left(\dfrac{-\cos \left(\frac{2 x+h}{2} \right)}{\sin \left(x+h \right) \sin x} \right) \lim _ {\frac{h}{2} \rightarrow 0} \dfrac{\sin \left(\frac{h}{2} \right)}{\left(\frac{h}{2} \right)} \\ \\ & =\left(\dfrac{-\cos x}{\sin x \sin x} \right) \cdot 1 \\ \\ & =-cosec \ x \cot x \end{aligned} $$
(v) मान लीजिए $f\left(x \right)=3 \cot x+5 cosec \ x$.
इसलिए, पहले सिद्धांत से,
$$ \qquad \begin{aligned} f^{\prime}\left(x \right) & =\lim _ {h \rightarrow 0} \dfrac{f\left(x+h \right)-f\left(x \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{3 \cot \left(x+h \right)+5 cosec \ \left(x+h \right)-3 \cot x-5 cosec \ x}{h} \\ \\ & =3 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\cot \left(x+h \right)-\cot x\right]+5 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[cosec \ \left(x+h \right)-cosec \ x\right] \qquad …(1) \end{aligned} $$
अब,
$$ \begin{aligned} \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\cot \left(x+h \right)-\cot x\right] & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\cos \left(x+h \right)}{\sin \left(x+h \right)}-\dfrac{\cos x}{\sin x}\right] \\ \\ $$
& =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\cos \left(x+h \right) \sin x-\cos x \sin \left(x+h \right)}{\sin x \sin \left(x+h \right)}\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x-x-h \right)}{\sin x \sin \left(x+h \right)}\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\sin \left(-h \right)}{\sin x \sin \left(x+h \right)}\right] \\ \\ & =-\left(\lim _ {h \rightarrow 0} \dfrac{\sin h}{h} \right) \cdot\left(\lim _ {h \rightarrow 0} \dfrac{1}{\sin x \cdot \sin \left(x+h \right)} \right) \\ \\ & =-1 \cdot \dfrac{1}{\sin x \cdot \sin \left(x+0 \right)}=\dfrac{-1}{\sin ^{2} x}=-cosec \ ^{2} x \quad\quad … (2) \\ \ \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[cosec \ \left(x+h \right)-cosec \ x\right] & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{1}{\sin \left(x+h \right)}-\dfrac{1}{\sin x}\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\sin x-\sin \left(x+h \right)}{\sin \left(x+h \right) \sin x}\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{2 \cos \left(\dfrac{x+x+h}{2} \right) \cdot \sin \left(\dfrac{x-x-h}{2} \right)}{\sin \left(x+h \right) \sin x}\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{2 \cos \left(\dfrac{2 x+h}{2} \right) \sin \left(-\dfrac{h}{2} \right)}{\sin \left(x+h \right) \sin x}\right] \\ \\ & \lim_ {h\rightarrow 0}\left[\dfrac{-\cos \left(\frac{2 x+h}{2} \right) \cdot \dfrac{\sin \left(\frac{h}{2} \right)}{\left(\frac{h}{2} \right)}}{\sin \left(x+h \right) \sin x}\right] \\ \\ & =\lim _ {h \rightarrow 0}\left(\dfrac{-\cos \left(\frac{2 x+h}{2} \right)}{\sin \left(x+h \right) \sin x} \right) \lim _ {\frac{h}{2} \rightarrow 0} \dfrac{\sin \left(\frac{h}{2} \right)}{\left(\frac{h}{2} \right)} \\ \\ & =\left(\dfrac{-\cos x}{\sin x \sin x} \right) \cdot 1 \\ \\ & =-cosec \ x \cot x \qquad\qquad …(3) \end{aligned} $
(1), (2) और (3) से, हम प्राप्त करते हैं
$ f^{\prime}\left(x \right)=-3 \cosec^{2} x-5 \cosec \ x \cot x $
$(vi)$ मान लीजिए, $f\left(x \right)=5 \sin x$ - $6 \cos x+7$.
इसलिए, पहले सिद्धांत से,
$ \begin{aligned} f^{\prime}\left(x \right) & =\lim _ {h \rightarrow 0} \dfrac{f\left(x+h \right)-f\left(x \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[5 \sin \left(x+h \right)-6 \cos \left(x+h \right)+7-5 \sin x+6 \cos x-7\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[5 \lbrace \sin \left(x+h \right)-\sin x \rbrace -6 \lbrace \cos \left(x+h \right)-\cos x \rbrace \right] \\ \\ & =5 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\sin \left(x+h \right)-\sin x\right]-6 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\cos \left(x+h \right)-\cos x\right] \\ \\ & =5 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[2 \cos \left(\dfrac{x+h+x}{2} \right) \sin \left(\dfrac{x+h-x}{2} \right)\right]-6 \lim _ {h \rightarrow 0} \dfrac{\cos x \cos h-\sin x \sin h-\cos x}{h} \\ \\ & =5 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[2 \cos \left(\dfrac{2 x+h}{2} \right) \sin \dfrac{h}{2}\right]-6 \lim _ {h \rightarrow 0}\left[\dfrac{-\cos x\left(1-\cos h \right)-\sin x \sin h}{h}\right] \\ \\ & =5 \lim _ {h \rightarrow 0}\left(\cos \left(\dfrac{2 x+h}{2} \right) \dfrac{\sin \frac{h}{2}}{\frac{h}{2}} \right)-6 \lim _ {h \rightarrow 0}\left[\dfrac{-\cos x\left(1-\cos h \right)}{h}-\dfrac{\sin x \sin h}{h}\right] \\ \\ & =5\left[\lim _ {h \rightarrow 0} \cos \left(\dfrac{2 x+h}{2} \right)\right]\left[\lim_ {a\rightarrow 0}\dfrac{\sin \frac{h}{2}}{\frac{h}{2}}\right]-6\left[\left(-\cos x \right)\left(\lim _ {h \rightarrow 0} \dfrac{1-\cos h}{h} \right)-\sin x \lim _ {h \rightarrow 0}\left(\dfrac{\sin h}{h} \right)\right] \\ \\ & =5 \cos x \cdot 1-6\left[\left(-\cos x \right) \cdot\left(0 \right)-\sin x \cdot 1\right] \\ \\ & =5 \cos x+6 \sin x \end{aligned} $
(vii) मान लीजिए $f\left(x \right)=2 \tan x$ - $7 \sec x$.
इसलिए, पहले सिद्धांत से,
$ \begin{aligned}
f^{\prime}\left(x \right) & =\lim _ {h \rightarrow 0} \dfrac{f\left(x+h \right)-f\left(x \right)}{h} \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[2 \tan \left(x+h \right)-7 \sec \left(x+h \right)-2 \tan x+7 \sec x\right] \\ \\ & =\lim _ {h \rightarrow 0} \dfrac{1}{h}\left[2 \lbrace \tan \left(x+h \right)-\tan x \rbrace -7 \lbrace \sec \left(x+h \right)-\sec x \rbrace \right] \\ \\ & =2 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\tan \left(x+h \right)-\tan x\right]-7 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\sec \left(x+h \right)-\sec x\right] \\ \\ & =2 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x+h \right)}{\cos \left(x+h \right)}-\dfrac{\sin x}{\cos x}\right]-7 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{1}{\cos \left(x+h \right)}-\dfrac{1}{\cos x}\right] \\ \\ & =2 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x+h \right) \cos x-\sin x \cos \left(x+h \right)}{\cos x \cos \left(x+h \right)}\right]-7 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\cos x-\cos \left(x+h \right)}{\cos x \cos \left(x+h \right)}\right] \\ \\ & =2 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x+h-x \right)}{\cos x \cos \left(x+h \right)}\right]-7 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{-2 \sin \left(\dfrac{x+x+h}{2} \right) \sin \left(\dfrac{x-x-h}{2} \right)}{\cos x \cos \left(x+h \right)}\right] \\ \\ & =2 \lim _ {h \rightarrow 0}\left[\left(\dfrac{\sin h}{h} \right) \dfrac{1}{\cos x \cos \left(x+h \right)}\right]-7 \lim _ {h \rightarrow 0} \dfrac{1}{h}\left[\dfrac{-2 \sin \left(\dfrac{2 x+h}{2} \right) \sin \left(-\dfrac{h}{2} \right)}{\cos x \cos \left(x+h \right)}\right] \\ \\ & =2\lim _ {h \rightarrow 0} \left(\dfrac{\sin h}{h} \right)\lim _ {h \rightarrow 0} \left(\dfrac{1}{\cos x \cos \left(x+h \right)} \right)-7\lim _ {\frac{h}{2} \rightarrow 0} \left(\dfrac{\sin \frac{h}{2}}{\frac{h}{2}} \right)\lim _ {h \rightarrow 0} \left(\dfrac{\sin \left(\frac{2 x+h}{2} \right)}{\cos x \cos \left(x+h \right)} \right) \\ \\
& =2\times 1 \times \dfrac{1}{\cos x \cos x}-7\times 1\left(\dfrac{\sin x}{\cos x \cos x} \right) \\ \\ & =2 \sec ^{2} x-7 \sec x \tan x \end{aligned} $
अतिरिक्त उदाहरण
उदाहरण 19 पहले सिद्धांत से $f$ के अवकलज को ज्ञात कीजिए, जहाँ $f$ निम्नलिखित द्वारा दिया गया है
(i) $f(x)=\dfrac{2 x+3}{x-2}$
(ii) $f(x)=x+\dfrac{1}{x}$
हल (i) ध्यान दें कि फलन $x=2$ पर परिभाषित नहीं है। लेकिन, हम निम्नलिखित कर सकते हैं
$ \begin{aligned} f^{\prime}(x)&=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \dfrac{\dfrac{2(x+h)+3}{x+h-2}-\dfrac{2 x+3}{x-2}}{h} \\ \\
& =\lim\limits_{h \to 0} \dfrac{(2 x+2 h+3)(x-2)-(2 x+3)(x+h-2)}{h(x-2)(x+h-2)} \\ \\ & =\lim\limits_{h \to 0} \dfrac{(2 x+3)(x-2)+2 h(x-2)-(2 x+3)(x-2)-h(2 x+3)}{h(x-2)(x+h-2)} \\ \\ & =\lim\limits_{h \to 0} \dfrac{-7}{(x-2)(x+h-2)}=-\dfrac{7}{(x-3)^{2}} \end{aligned} $
फिर भी ध्यान दें कि फलन $f^{\prime}$ $x=2$ पर भी परिभाषित नहीं है।
(ii) फलन $x=0$ पर परिभाषित नहीं है। लेकिन हम यह भी जानते हैं कि
$ \begin{aligned} f^{\prime}(x) & =\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \dfrac{\left(x+h+\dfrac{1}{x+h}\right)-\left(x+\dfrac{1}{x}\right)}{h} \\ \\
$$ \begin{aligned} & =\lim\limits_{h \to 0} \dfrac{1}{h}\left[h+\dfrac{1}{x+h}-\dfrac{1}{x}\right] \\ \\ & =\lim\limits_{h \to 0} \dfrac{1}{h}\left[h+\dfrac{x-x-h}{x(x+h)}\right]=\lim\limits_{h \to 0} \dfrac{1}{h}\left[h\left(1-\dfrac{1}{x(x+h)}\right)\right] \\ \\ & =\lim\limits_{h \to 0}\left[1-\dfrac{1}{x(x+h)}\right]=1-\dfrac{1}{x^{2}} \end{aligned} $$
फिर भी ध्यान दें कि फलन $f^{\prime}$, $x=0$ पर निर्धारित नहीं होता।
उदाहरण 20 $f(x)$ के अवकलज को प्रथम सिद्धांत से ज्ञात कीजिए, जहाँ $f(x)$ है
(i) $\sin x+\cos x$
(ii) $x \sin x$
हल (i) हम जानते हैं $f^{\prime}(x)=\dfrac{f(x+h)-f(x)}{h}$
$ \begin{aligned} & =\lim\limits_{h \to 0} \dfrac{\sin (x+h)+\cos (x+h)-\sin x-\cos x}{h} \\ & =\lim\limits_{h \to 0} \dfrac{\sin x \cos h+\cos x \sin h+\cos x \cos h-\sin x \sin h-\sin x-\cos x}{h} \end{aligned} $
$ \begin{aligned} & =\lim\limits_{h \to 0} \dfrac{\sin h(\cos x-\sin x)+\sin x(\cos h-1)+\cos x(\cos h-1)}{h} \\ & =\lim\limits_{h \to 0} \dfrac{\sin h}{h}(\cos x-\sin x)+\lim\limits_{h \to 0} \sin x \dfrac{(\cos h-1)}{h}+\lim\limits_{h \to 0} \cos x \dfrac{(\cos h-1)}{h} \\
& =\cos x-\sin x \end{aligned} $
(ii) $\quad f^{\prime}(x)=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \dfrac{(x+h) \sin (x+h)-x \sin x}{h}$
$ =\lim\limits_{h \to 0} \dfrac{(x+h)(\sin x \cos h+\sin h \cos x)-x \sin x}{h} $
$ \begin{aligned} & =\lim\limits_{h \to 0} \dfrac{x \sin x(\cos h-1)+x \cos x \sin h+h(\sin x \cos h+\sin h \cos x)}{h} \\ & =\lim\limits_{h \to 0} \dfrac{x \sin x(\cos h-1)}{h}+\lim\limits_{h \to 0} x \cos x \dfrac{\sin h}{h}+\lim\limits_{h \to 0}(\sin x \cos h+\sin h \cos x) \\
& =x \cos x+\sin x \end{aligned} $
उदाहरण 21 के अवकलज की गणना करें
(i) $f(x)=\sin 2 x$
(ii) $g(x)=\cot x$
हल (i) याद रखें त्रिकोणमितीय सूत्र $\sin 2 x=2 \sin x \cos x$. इसलिए
$ \begin{aligned} \dfrac{d f(x)}{d x} & =\dfrac{d}{d x}(2 \sin x \cos x)=2 \dfrac{d}{d x}(\sin x \cos x) \\ \\ & =2\left[(\sin x)^{\prime} \cos x+\sin x(\cos x)^{\prime}\right] \\ \\ & =2\left[(\cos x) \cos x+\sin x(-\sin x)\right] \\ \\ & =2(\cos ^{2} x-\sin ^{2} x) \end{aligned} $
(ii) परिभाषा के अनुसार, $g(x)=\cot x=\dfrac{\cos x}{\sin x}$. हम इस फ़ंक्शन पर भाग नियम का उपयोग करते हैं
कहीं भी परिभाषित है। $\dfrac{d g}{d x}=\dfrac{d}{d x}(\cot x)=\dfrac{d}{d x}\left(\dfrac{\cos x}{\sin x}\right)$
$ \begin{aligned} & =\dfrac{(\cos x)^{\prime}(\sin x)-(\cos x)(\sin x)^{\prime}}{(\sin x)^{2}} \\ & =\dfrac{(-\sin x)(\sin x)-(\cos x)(\cos x)}{(\sin x)^{2}} \\ & =-\dfrac{\sin ^{2} x+\cos ^{2} x}{\sin ^{2} x}=-cosec^{2} x \end{aligned} $
अलग-अलग, इसे ध्यान में रखते हुए गणना किया जा सकता है कि $\cot x=\dfrac{1}{\tan x}$. यहाँ, हम यह तथ्य का उपयोग करते हैं कि $\tan x$ का अवकलज $\sec ^{2} x$ होता है, जिसे उदाहरण 17 में देखा गया था, और इसके अलावा, नियत फलन के अवकलज शून्य होता है।
$ \begin{aligned} \dfrac{d g}{d x} & =\dfrac{d}{d x}(\cot x)=\dfrac{d}{d x}\left(\dfrac{1}{\tan x}\right) \\ & =\dfrac{(1)^{\prime}(\tan x)-(1)(\tan x)^{\prime}}{(\tan x)^{2}} \\ & =\dfrac{(0)(\tan x)-(\sec x)^{2}}{(\tan x)^{2}} \\ & =\dfrac{-\sec ^{2} x}{\tan ^{2} x}=-cosec^{2} x \end{aligned} $
उदाहरण 22 निम्नलिखित के अवकलज ज्ञात कीजिए
(i) $\dfrac{x^{5}-\cos x}{\sin x}$
(ii) $\dfrac{x+\cos x}{\tan x}$
हल (i) मान लीजिए $h(x)=\dfrac{x^{5}-\cos x}{\sin x}$. इस फलन के अवकलज के लिए हम इसके परिभाषित क्षेत्र में भाग नियम का उपयोग करते हैं।
$ h^{\prime}(x)=\dfrac{(x^{5}-\cos x)^{\prime} \sin x-(x^{5}-\cos x)(\sin x)^{\prime}}{(\sin x)^{2}} $
$ \begin{aligned} & =\dfrac{(5 x^{4}+\sin x) \sin x-(x^{5}-\cos x) \cos x}{\sin ^{2} x} \\ & =\dfrac{-x^{5} \cos x+5 x^{4} \sin x+1}{(\sin x)^{2}} \end{aligned} $
(ii) हम फलन $\dfrac{x+\cos x}{\tan x}$ के लिए जहाँ भी यह परिभाषित है, इस पर आंशिक नियम का उपयोग करते हैं।
$ \begin{aligned} h^{\prime}(x) & =\dfrac{(x+\cos x)^{\prime} \tan x-(x+\cos x)(\tan x)^{\prime}}{(\tan x)^{2}} \\ & =\dfrac{(1-\sin x) \tan x-(x+\cos x) \sec ^{2} x}{(\tan x)^{2}}
\end{aligned} $
अध्याय 12 पर अतिरिक्त अभ्यास
1. निम्नलिखित फलनों के अवकलज पहले सिद्धांत से ज्ञात कीजिए:
(i) $-x$
(ii) $\left(-x\right)^{-1}$
(iii) $\sin \left(x+1\right)$
(iv) $\cos \left(x-\dfrac{\pi}{8}\right)$
उत्तर दिखाएँ
उत्तर :
(i) मान लीजिए $f\left(x\right)=- x$. अतः, $f\left(x+h\right)=-\left(x+h\right)$
पहले सिद्धांत से,
$ \begin{aligned} f^{\prime}\left(x\right) & =\lim _ {h \to 0} \dfrac{f\left(x+h\right)-f\left(x\right)}{h} \\ \\ & =\lim _ {h \to 0} \dfrac{-\left(x+h\right)-\left(-x\right)}{h} \\ \\ & =\lim _ {h \to 0} \dfrac{-x-h+x}{h} \\ \\ & =\lim _ {h \to 0} \dfrac{-h}{h} \\ \\ & =\lim _ {h \to 0}\left(-1\right)=-1 \end{aligned} $
$\mathrm{(ii) \ मान लीजिए,} \quad f \left(x\right)=\left(-x\right)^{-1}=\dfrac{1}{-x}=\dfrac{-1}{x} $
$\text{अतः, } \ f \left(x+h\right)=\dfrac{-1}{\left(x+h\right)} $
पहले सिद्धांत से,
$ \begin{aligned} f^{\prime}\left(x\right) & =\lim _ {h \to 0} \dfrac{f\left(x+h\right)-f\left(x\right)}{h} \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{-1}{x+h}-\left(\dfrac{-1}{x}\right)\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{-1}{x+h}+\dfrac{1}{x}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{-x+\left(x+h\right)}{x\left(x+h\right)}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{-x+x+h}{x\left(x+h\right)}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{h}{x\left(x+h\right)}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{x\left(x+h\right)} \\ \\ & =\dfrac{1}{x \cdot x}=\dfrac{1}{x^{2}} \end{aligned} $
$\mathrm{(iii) ~ मान लीजिए,} \quad f\left(x\right)=\sin \left(x+1\right)$
अतः, $f\left(x+h\right)=\sin \left(x+h+1\right)$
पहले सिद्धांत से,
$ \begin{aligned} f^{\prime}\left(x\right) & =\lim _ {h \to 0} \dfrac{f\left(x+h\right)-f\left(x\right)}{h} \\ \\
& =\lim _ {h \to 0} \dfrac{1}{h}\left[\sin \left(x+h+1\right)-\sin \left(x+1\right)\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[2 \cos \left(\dfrac{x+h+1+x+1}{2}\right) \sin \left(\dfrac{x+h+1-x-1}{2}\right)\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[2 \cos \left(\dfrac{2 x+h+2}{2}\right) \sin \left(\dfrac{h}{2}\right)\right] \\ \\ & =\lim _ {h \to 0}\left[\cos \left(\dfrac{2 x+h+2}{2}\right) \cdot \dfrac{\sin \left(\frac{h}{2}\right)}{\left(\frac{h}{2}\right)}\right] \\ \\ & =\lim _ {h \to 0} \cos \left(\dfrac{2 x+h+2}{2}\right) \times \lim _ {\frac{h}{2} \to 0} \left[\dfrac{\sin\frac{h}{2}}{\frac{h}{2}}\right] \\ \\ & =\cos \left(\dfrac{2 x+0+2}{2}\right) \times 1 \\ \\ & =\cos \left(x+1\right) \\ \\ f\left(x\right) & =\cos \left(x-\dfrac{\pi}{8}\right) \quad \text{ Accordingly, } \end{aligned} $
प्रथम सिद्धांत से,
$ \begin{aligned} f^{\prime}\left(x\right) & =\lim _ {h \to 0} \dfrac{f\left(x+h\right)-f\left(x\right)}{h} \\ \\ & \ =\lim _ {h \to 0} \dfrac{1}{h}\left[\cos \left(x+h-\dfrac{\pi}{8}\right)-\cos \left(x-\dfrac{\pi}{8}\right)\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[-2 \sin \dfrac{\left(x+h-\dfrac{\pi}{8}+x-\dfrac{\pi}{8}\right)}{2} \sin \left(\dfrac{x+h-\dfrac{\pi}{8}-x+\dfrac{\pi}{8}}{2}\right)\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[-2 \sin \left(\dfrac{2 x+h-\dfrac{\pi}{4}}{2}\right) \sin \dfrac{h}{2}\right] \\ \\ & =\lim _ {h \to 0}\left[-\sin \left(\dfrac{2 x+h-\dfrac{\pi}{4}}{2}\right) \dfrac{\sin \left(\frac{h}{2}\right)}{\left(\frac{h}{2}\right)}\right] \\ \\ & =\lim _ {h \to 0}\left[-\sin \left(\dfrac{2 x+h-\frac{\pi}{4}}{2}\right)\right] \times\lim _ {\frac{h}{2} \to 0}\left(\dfrac{\sin \left(\frac{h}{2}\right)}{\left(\frac{h}{2}\right)}\right) \hspace{30px} \left[\because \ \ \text{As } h \to 0 \Rightarrow \dfrac{h}{2} \to 0\right] \end{aligned} $
$ \begin{aligned} & \quad \ =-\sin \left(\dfrac{2 x+0-\dfrac{\pi}{4}}{2}\right) \times 1 \\ \\ & \quad \ =-\sin \left(x-\dfrac{\pi}{8}\right)
\end{aligned} $
निम्नलिखित फलनों का अवकलज ज्ञात कीजिए (यह समझा जाता है कि $a, b, c, d$, $p, q, r$ और $s$ स्थिर गैर-शून्य नियतांक हैं और $m$ और $n$ पूर्णांक हैं):
2. $\left(x+a\right)$
उत्तर दिखाएं
उत्तर :
मान लीजिए $f\left(x\right)=x+a$. इस प्रकार, $f\left(x+h\right)=x+h+a$
पहले सिद्धांत के अनुसार,
$ \begin{aligned} f^{\prime}\left(x\right) & =\lim _ {h \to 0} \dfrac{f\left(x+h\right)-f\left(x\right)}{h} \\ \\ & =\lim _ {h \to 0} \dfrac{x+h+a-x-a}{h} \\ \\ & =\lim _ {h \to 0}\left(\dfrac{h}{h}\right) \\ \\ & =\lim _ {h \to 0}\left(1\right) \\ \\ & =1 \end{aligned} $
3. $\left(p x+q\right)\left(\dfrac{r}{x}+s\right)$
उत्तर दिखाएं
उत्तर :
मान लीजिए $f\left(x\right)=\left(p x+q\right)\left(\dfrac{r}{x}+s\right)$
लेब्निज गुणन नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x\right) & =\left(p x+q\right)\left(\dfrac{r}{x}+s\right)^{\prime}+\left(\dfrac{r}{x}+s\right)\left(p x+q\right)^{\prime} \\ \\ & =\left(p x+q\right)\left(r x^{-1}+s\right)^{\prime}+\left(\dfrac{r}{x}+s\right)\left(p\right) \\ \\ & =\left(p x+q\right)\left(-r x^{-2}\right)+\left(\dfrac{r}{x}+s\right) p \\ \\ & =\left(p x+q\right)\left(\dfrac{-r}{x^{2}}\right)+\left(\dfrac{r}{x}+s\right) p \\ \\ & =\dfrac{-p r}{x}-\dfrac{q r}{x^{2}}+\dfrac{p r}{x}+p s \\ \\ & =p s-\dfrac{q r}{x^{2}} \end{aligned} $
4. $\left(a x+b\right)\left(c x+d\right)^{2}$
उत्तर दिखाएं
उत्तर :
मान लीजिए $f\left(x\right)=\left(a x+b\right)\left(c x+d\right)^{2}$
लेब्निज गुणन नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x\right) & =\left(a x+b\right) \dfrac{d}{d x}\left(c x+d\right)^{2}+\left(c x+d\right)^{2} \dfrac{d}{d x}\left(a x+b\right) \\ \\ & =\left(a x+b\right) \dfrac{d}{d x}\left(c^{2} x^{2}+2 c d x+d^{2}\right)+\left(c x+d\right)^{2} \dfrac{d}{d x}\left(a x+b\right) \\ \\ & =\left(a x+b\right)\left[\dfrac{d}{d x}\left(c^{2} x^{2}\right)+\dfrac{d}{d x}\left(2 c d x\right)+\dfrac{d}{d x} d^{2}\right]+\left(c x+d\right)^{2}\left[\dfrac{d}{d x} a x+\dfrac{d}{d x} b\right] \\ \\
& =\left(a x+b\right)\left(2 c^{2} x+2 c d\right)+\left(c x+d^{2}\right) a \\ \\ & =2 c\left(a x+b\right)\left(c x+d\right)+a\left(c x+d\right)^{2} \end{aligned} $
5. $\dfrac{a x+b}{c x+d}$
उत्तर दिखाएं
Answer :
Let $f\left(x\right)=\dfrac{a x+b}{c x+d}$
By quotient rule,
$ \begin{aligned} f^{\prime}\left(x\right) & =\dfrac{\left(c x+d\right) \dfrac{d}{d x}\left(a x+b\right)-\left(a x+b\right) \dfrac{d}{d x}\left(c x+d\right)}{\left(c x+d\right)^{2}} \\ \\ & =\dfrac{\left(c x+d\right)\left(a\right)-\left(a x+b\right)\left(c\right)}{\left(c x+d\right)^{2}} \\ \\ & =\dfrac{a c x+a d-a c x-b c}{\left(c x+d\right)^{2}} \\ \\ & =\dfrac{a d-b c}{\left(c x+d\right)^{2}} \end{aligned} $
6. $\dfrac{1+\dfrac{1}{x}}{1-\dfrac{1}{x}}$
उत्तर दिखाएं
Answer :
Let $f\left(x\right)=\dfrac{1+\dfrac{1}{x}}{1-\dfrac{1}{x}}=\dfrac{\dfrac{x+1}{x}}{\dfrac{x-1}{x}}=\dfrac{x+1}{x-1}$, where $x \neq 0$
By quotient rule,
$ \begin{aligned} f^{\prime}\left(x\right) & =\dfrac{\left(x-1\right) \dfrac{d}{d x}\left(x+1\right)-\left(x+1\right) \dfrac{d}{d x}\left(x-1\right)}{\left(x-1\right)^{2}}, x \neq 0,1 \\ \\ & =\dfrac{\left(x-1\right)\left(1\right)-\left(x+1\right)\left(1\right)}{\left(x-1\right)^{2}}, x \neq 0,1 \\ \\ & =\dfrac{x-1-x-1}{\left(x-1\right)^{2}}, x \neq 0,1 \\ \\ & =\dfrac{-2}{\left(x-1\right)^{2}}, x \neq 0,1 \end{aligned} $
7. $\dfrac{1}{a x^{2}+b x+c}$
उत्तर दिखाएं
Answer :
Let $f\left(x\right)=\dfrac{1}{a x^{2}+b x+c}$
By quotient rule,
$ \begin{aligned} f^{\prime}\left(x\right) & =\dfrac{\left(a x^{2}+b x+c\right) \dfrac{d}{d x}\left(1\right)-\dfrac{d}{d x}\left(a x^{2}+b x+c\right)}{\left(a x^{2}+b x+c\right)^{2}} \\ \\ & =\dfrac{\left(a x^{2}+b x+c\right)\left(0\right)-\left(2 a x+b\right)}{\left(a x^{2}+b x+c\right)^{2}} \\ \\ & =\dfrac{-\left(2 a x+b\right)}{\left(a x^{2}+b x+c\right)^{2}} \end{aligned}
$
8. $\dfrac{a x+b}{p x^{2}+q x+r}$
उत्तर दिखाएं
उत्तर :
मान लीजिए $f\left(x\right)=\dfrac{a x+b}{p x^{2}+q x+r}$
भाग नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x\right) & =\dfrac{\left(p x^{2}+q x+r\right) \dfrac{d}{d x}\left(a x+b\right)-\left(a x+b\right) \dfrac{d}{d x}\left(p x^{2}+q x+r\right)}{\left(p x^{2}+q x+r\right)^{2}} \\ \\ & =\dfrac{\left(p x^{2}+q x+r\right)\left(a\right)-\left(a x+b\right)\left(2 p x+q\right)}{\left(p x^{2}+q x+r\right)^{2}} \\ \\ & =\dfrac{a p x^{2}+a q x+a r-2 a p x^{2}-a q x-2 b p x-b q}{\left(p x^{2}+q x+r\right)^{2}} \\ \\ & =\dfrac{-a p x^{2}-2 b p x+a r-b q}{\left(p x^{2}+q x+r\right)^{2}} \end{aligned} $
9. $\dfrac{p x^{2}+q x+r}{a x+b}$
उत्तर दिखाएं
उत्तर :
मान लीजिए $f\left(x\right)=\dfrac{p x^{2}+q x+r}{a x+b}$
भाग नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x\right) & =\dfrac{\left(a x+b\right) \dfrac{d}{d x}\left(p x^{2}+q x+r\right)-\left(p x^{2}+q x+r\right) \dfrac{d}{d x}\left(a x+b\right)}{\left(a x+b\right)^{2}} \\ \\ & =\dfrac{\left(a x+b\right)\left(2 p x+q\right)-\left(p x^{2}+q x+r\right)\left(a\right)}{\left(a x+b\right)^{2}} \\ \\ & =\dfrac{2 a p x^{2}+a q x+2 b p x+b q-a p x^{2}-a q x-a r}{\left(a x+b\right)^{2}} \\ \\ & =\dfrac{a p x^{2}+2 b p x+b q-a r}{\left(a x+b\right)^{2}} \end{aligned} $
10. $\dfrac{a}{x^{4}}-\dfrac{b}{x^{2}}+\cos x$
उत्तर दिखाएं
उत्तर :
$ \begin{aligned} \text{ मान लीजिए } f\left(x\right) & =\dfrac{a}{x^{4}}-\dfrac{b}{x^{2}}+\cos x \\ \\ f^{\prime}\left(x\right) & =\dfrac{d}{d x}\left(\dfrac{a}{x^{4}}\right)-\dfrac{d}{d x}\left(\dfrac{b}{x^{2}}\right)+\dfrac{d}{d x}\left(\cos x\right) \\ \\ & =a \dfrac{d}{d x}\left(x^{-4}\right)-b \dfrac{d}{d x}\left(x^{-2}\right)+\dfrac{d}{d x}\left(\cos x\right) \\ \\ & =a\left(-4 x^{-5}\right)-b\left(-2 x^{-3}\right)+\left(-\sin x\right) \quad\left[\dfrac{d}{d x}\left(x^{n}\right)=n x^{n-1} \text{ और } \dfrac{d}{d x}\left(\cos x\right)=-\sin x\right] \\ \\
& =\dfrac{-4 a}{x^{5}}+\dfrac{2 b}{x^{3}}-\sin x \end{aligned} $
11. $4 \sqrt{x}-2$
उत्तर दिखाएं
Answer :
$ \begin{aligned} & \text{ मान लीजिए, } \ f\left(x\right)=4 \sqrt{x}-2 \\ \\ & \begin{aligned} \qquad f^{\prime}\left(x\right) & =\dfrac{d}{d x}\left(4 \sqrt{x}-2\right)=\dfrac{d}{d x}\left(4 \sqrt{x}\right)-\dfrac{d}{d x}\left(2\right) \\ \\ & =4 \dfrac{d}{d x}\left(x^{\frac{1}{2}}\right)-0=4\left(\dfrac{1}{2} x^{\frac{1}{2}-1}\right) \\ \\ & =\left(2 x^{-\frac{1}{2}}\right)=\dfrac{2}{\sqrt{x}} \end{aligned} \end{aligned} $
12. $\left(a x+b\right)^{n}$
उत्तर दिखाएं
Answer :
Let $f\left(x\right)=\left(a x+b\right)^{n}$
Accordingly, $f\left(x+h\right)=\left \lbrace a\left(x+h\right)+b\right \rbrace ^{n}=\left(a x+a h+b\right)^{n}$ By first principle,
$ \begin{aligned} f^{\prime}\left(x\right) & =\lim _ {h \to 0} \dfrac{f\left(x+h\right)-f\left(x\right)}{h} \\ \\ & =\lim _ {h \to 0} \dfrac{\left(a x+a h+b\right)^{n}-\left(a x+b\right)^{n}}{h} \\ \\ & =\lim _ {h \to 0} \dfrac{\left(a x+b\right)^{n}\left(1+\dfrac{a h}{a x+b}\right)^{n}-\left(a x+b\right)^{n}}{h} \\ \\ & =\left(a x+b\right)^{n} \lim _ {h \to 0} \dfrac{\left(1+\dfrac{a h}{a x+b}\right)^{n}-1}{h} \\ \\ & =\left(a x+b\right)^{n} \lim _ {h \to 0} \dfrac{1}{h}\left[\left \lbrace 1+n\left(\dfrac{a h}{a x+b}\right)+\dfrac{n\left(n-1\right)}{\lfloor 2}\left(\dfrac{a h}{a x+b}\right)^{2}+\ldots\right \rbrace -1\right] \\ \\ & =\left(a x+b\right)^{n} \lim _ {h \to 0}\left[\dfrac{na}{ax+b}+\dfrac{n(n-1)}{\lfloor 2}\times \dfrac{a^2h}{(ax+b)^2}\right]+\ldots\left(\text{ Terms containing higher degrees of } h\right) \\ \\ & =\left(a x+b\right)^{n} \lim _ {h \to 0}\left[\dfrac{n a}{\left(a x+b\right)}+\dfrac{n\left(n-1\right) a^{2} h}{\lfloor 2\left(a x+b\right)^{2}}+\ldots\right] \\ \\ & =\left(a x+b\right)^{n}\left[\dfrac{n a}{\left(a x+b\right)}+0\right] \\ \\ & =n a \dfrac{\left(a x+b\right)^{n}}{\left(a x+b\right)}\left[(a x+b)^{n-1}\right]
\end{aligned} $
13. $\left(a x+b\right)^{n}\left(c x+d\right)^{m}$
उत्तर दिखाएं
Answer :
Let $f\left(x\right)=\left(a x+b\right)^{n}\left(c x+d\right)^{m}$
By Leibnitz product rule,
$ \begin{aligned} f^{\prime}\left(x\right)=\left(a x+b\right)^{n} \dfrac{d}{d x}\left(c x+d\right)^{m}+\left(c x+d\right)^{m} \dfrac{d}{d x}\left(a x+b\right)^{n} \qquad \ldots{(1)} \end{aligned} $
$\text{Let,} \ \ f_1\left(x\right)=\left(c x+d\right)^{m}$
$\text{Now, } \ \ f_1\left(x+h\right)=\left(c x+c h+d\right)^{m}$
$f_1^{\prime}\left(x\right)=\lim _ {h \to 0} \dfrac{f_1\left(x+h\right)-f_1^{\prime}\left(x\right)}{h}$
$\hspace{1cm}=\lim _ {h \to 0} \dfrac{\left(c x+c h+d\right)^{m}-\left(c x+d\right)^{m}}{h}$
$\hspace{1cm}=\left(c x+d\right)^{m} \lim _ {h \to 0} \dfrac{1}{h}\left[\left(1+\dfrac{c h}{c x+d}\right)^{m}-1\right]$
$\hspace{1cm}=\left(c x+d\right)^{m} \lim _ {h \to 0} \dfrac{1}{h}\left[\left(1+\dfrac{m c h}{\left(c x+d\right)}+\dfrac{m\left(m-1\right)}{2} \dfrac{\left(c^{2} h^{2}\right)}{\left(c x+d\right)^{2}}+\ldots\right)-1\right]$
$\hspace{1cm}=\left(c x+d\right)^{m} \lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{m c h}{\left(c x+d\right)}+\dfrac{m\left(m-1\right) c^{2} h^{2}}{2\left(c x+d\right)^{2}}+\ldots\left( \text{ Terms containing higher degrees of} \ h\right)\right]$
$\hspace{1cm}=\left(c x+d\right)^{m} \lim _ {h \to 0}\left[\dfrac{m c}{\left(c x+d\right)}+\dfrac{m\left(m-1\right) c^{2} h}{2\left(c x+d\right)^{2}}+\ldots\right]$
$\hspace{1cm}=\left(c x+d\right)^{m}\left[\dfrac{m c}{c x+d}+0\right]$
$\hspace{1cm}=\dfrac{m c\left(c x+d\right)^{m}}{\left(c x+d\right)}$
$\hspace{1cm}=m c\left(c x+d\right)^{m-1}$
$\dfrac{d}{d x}\left(c x+d\right)^{It}=m c\left(c x+d\right)^{m-1}$
Similarly, $\dfrac{d}{d x}\left(a x+b\right)^{n}=n a\left(a x+b\right)^{n-1}$
Therefore, from $\left(1\right), \left(2\right), and \left(3\right),$ we obtain
$ \begin{aligned} f^{\prime}\left(x\right) & =\left(a x+b\right)^{n}\left \lbrace m c\left(c x+d\right)^{m-1}\right \rbrace +\left(c x+d\right)^{m}\left \lbrace n a\left(a x+b\right)^{n-1}\right \rbrace \\ \\
& =\left(a x+b\right)^{n-1}\left(c x+d\right)^{m-1}\left[m c\left(a x+b\right)+n a\left(c x+d\right)\right] \end{aligned} $
14. $\sin \left(x+a\right)$
उत्तर दिखाएं
Answer :
मान लीजिए $f\left(x\right)=\sin \left(x+a\right)$
$f\left(x+h\right)=\sin \left(x+h+a\right)$
प्रथम सिद्धांत से,
$ \begin{aligned} f^{\prime}\left(x\right) & =\lim _ {h \to 0} \dfrac{f\left(x+h\right)-f\left(x\right)}{h} \\ \\ & =\lim _ {h \to 0} \dfrac{\sin \left(x+h+a\right)-\sin \left(x+a\right)}{h} \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[2 \cos \left(\dfrac{x+h+a+x+a}{2}\right) \sin \left(\dfrac{x+h+a-x-a}{2}\right)\right] \\ \\ & =\lim _ {h \to \infty} \dfrac{1}{h}\left[2 \cos \left(\dfrac{2 x+2 a+h}{2}\right) \sin \left(\dfrac{h}{2}\right)\right] \\ \\ & =\lim _ {h \to 0}\left[\cos \left(\dfrac{2 x+2 a+h}{2}\right)\left \lbrace \dfrac{\sin \left(\frac{h}{2}\right)}{\left(\frac{h}{2}\right)}\right \rbrace \right] \\ \\ & =\lim _ {h \to 0} \cos \left(\dfrac{2 x+2 a+h}{2}\right) \lim _ {\frac{h}{2} \to 0}\left \lbrace \dfrac{\sin \left(\frac{h}{2}\right)}{\left(\frac{h}{2}\right)}\right \rbrace \quad\left[\text{ जैसे } h \to 0 \Rightarrow \dfrac{h}{2} \to 0\right] \\ \\ & =\cos \left(\dfrac{2 x+2 a}{2}\right) \times 1 \quad\left[\lim _ {x \to 0} \dfrac{\sin x}{x}=1\right] \\ \\ & =\cos \left(x+a\right) \end{aligned} $
15. $cosec \ x \cot x$
उत्तर दिखाएं
Answer :
$\text{मान लीजिए,}\quad f\left(x\right)=cosec \ x \cot x$
Leibnitz गुणन सूत्र से,
$f^{\prime}\left(x\right)=cosec \ x\left(\cot x\right)^{\prime}+\cot x\left(cosec \ x\right)^{\prime}$
$\text{मान लीजिए,}\quad f_1\left(x\right)=\cot x$. अतः, $f_1\left(x+h\right)=\cot \left(x+h\right)$
प्रथम सिद्धांत से,
$ \begin{aligned} f_1^{\prime}\left(x\right) & =\lim _ {h \to 0} \dfrac{f_1\left(x+h\right)-f_1\left(x\right)}{h} \\ \\ & =\lim _ {h \to 0} \dfrac{\cot \left(x+h\right)-\cot x}{h} \\ \\
& =\lim _ {h \to 0} \dfrac{1}{h}\left(\dfrac{\cos \left(x+h\right)}{\sin \left(x+h\right)}-\dfrac{\cos x}{\sin x}\right) \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin x \cos \left(x+h\right)-\cos x \sin \left(x+h\right)}{\sin x \sin \left(x+h\right)}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x-x-h\right)}{\sin x \sin \left(x+h\right)}\right] \\ \\ & =\dfrac{1}{\sin x} \cdot \lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin \left(-h\right)}{\sin \left(x+h\right)}\right] \\ \\ & =\dfrac{-1}{\sin x} \cdot\left(\lim _ {h \to 0} \dfrac{\sin h}{h}\right)\left(\lim _ {h \to 0} \dfrac{1}{\sin \left(x+h\right)}\right) \\ \\ & =\dfrac{-1}{\sin {x}} \cdot 1 \cdot\left(\dfrac{1}{\sin \left(x+0\right)}\right) \\ \\ & =\dfrac{-1}{\sin {2} x} \\ \\ & =-cosec \ ^{2} x \qquad \ldots{(2)} \end{aligned} $
$\therefore \ \ \left(\cot x\right)^{\prime}=-cosec \ ^{2} x$
अब, बर्बल $f_2\left(x\right)=cosec \ x$। इस प्रकार, $f_2\left(x+h\right)=cosec \ \left(x+h\right)$
पहले सिद्धांत के अनुसार,
$ \begin{aligned} f_2^{\prime}\left(x\right) & =\lim _ {h \to 0} \dfrac{f_2\left(x+h\right)-f_2\left(x\right)}{h} \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[cosec \ \left(x+h\right)-cosec \ x\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{1}{\sin \left(x+h\right)}-\dfrac{1}{\sin x}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin x-\sin \left(x+h\right)}{\sin x \sin \left(x+h\right)}\right] \\ \\ & =\dfrac{1}{\sin x} \cdot \lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{2 \cos \left(\dfrac{x+x+h}{2}\right) \sin \left(\dfrac{x-x-h}{2}\right)}{\sin \left(x+h\right)}\right] \\ \\ & =\dfrac{1}{\sin x} \cdot \lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{.2 \cos \left(\dfrac{2 x+h}{2}\right) \sin \left(\dfrac{-h}{2}\right)}{\sin \left(x+h\right)}\right] \\ \\ & =\dfrac{1}{\sin x} \cdot \lim _ {h \to 0}\left[\dfrac{-\sin \left(\dfrac{h}{2}\right)}{\left(\dfrac{h}{2}\right)} \cdot \dfrac{\cos \left(\dfrac{2 x+h}{2}\right)}{\sin \left(x+h\right)}\right] \\ \\
& =\dfrac{-1}{\sin x} \cdot \lim _ {h \to 0} \dfrac{\sin \left(\dfrac{h}{2}\right)}{\left(\dfrac{h}{2}\right)} \cdot \lim _ {h \to 0} \dfrac{\cos \left(\dfrac{2 x+h}{2}\right)}{\sin \left(x+h\right)} \\ \\ & =\dfrac{-1}{\sin x} \cdot 1 \cdot \dfrac{\cos \left(\dfrac{2 x+0}{2}\right)}{\sin \left(x+0\right)} \\ \\ & =\dfrac{-1}{\sin x} \cdot \dfrac{\cos x}{\sin x} \\ \\ & =-\cos ec x \cdot \cot x \qquad \ldots{(3)} \end{aligned} $
$\therefore \ \ \left(cosec \ x\right)^{\prime}=-cosec \ x \cdot \cot x$
समीकरण (1), (2), और (3) से, हम प्राप्त करते हैं
$ \begin{aligned} f^{\prime}\left(x\right) & =cosec \ x\left(-cosec \ ^{2} x\right)+\cot x\left(-cosec \ x \cot x\right) \\ \\ & =-cosec \ ^{3} x-\cot ^{2} x cosec \ x \end{aligned} $
16. $\dfrac{\cos x}{1+\sin x}$
उत्तर दिखाएं
Answer :
मान लीजिए $f\left(x\right)=\dfrac{\cos x}{1+\sin x}$
भाग नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x\right) & =\dfrac{\left(1+\sin x\right) \dfrac{d}{d x}\left(\cos x\right)-\left(\cos x\right) \dfrac{d}{d x}\left(1+\sin x\right)}{\left(1+\sin x\right)^{2}} \\ \\ & =\dfrac{\left(1+\sin x\right)\left(-\sin x\right)-\left(\cos x\right)\left(\cos x\right)}{\left(1+\sin x\right)^{2}} \\ \\ & =\dfrac{-\sin x-\sin ^{2} x-\cos ^{2} x}{\left(1+\sin x\right)^{2}} \\ \\ & =\dfrac{-\sin x-\left(\sin ^{2} x+\cos ^{2} x\right)}{\left(1+\sin x\right)^{2}} \\ \\ & =\dfrac{-\sin x-1}{\left(1+\sin x\right)^{2}} \\ \\ & =\dfrac{-\left(1+\sin x\right)}{\left(1+\sin x\right)^{2}} \\ \\ & =\dfrac{-1}{\left(1+\sin x\right)} \end{aligned} $
17. $\dfrac{\sin x+\cos x}{\sin x-\cos x}$
उत्तर दिखाएं
Answer :
मान लीजिए $f\left(x\right)=\dfrac{\sin x+\cos x}{\sin x-\cos x}$
भाग नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x\right) & =\dfrac{\left(\sin x-\cos x\right) \dfrac{d}{d x}\left(\sin x+\cos x\right)-\left(\sin x+\cos x\right) \dfrac{d}{d x}\left(\sin x-\cos x\right)}{\left(\sin x-\cos x\right)^{2}} \\ \\
& =\dfrac{\left(\sin x-\cos x\right)\left(\cos x-\sin x\right)-\left(\sin x+\cos x\right)\left(\cos x+\sin x\right)}{\left(\sin x-\cos x\right)^{2}} \\ \\ & =\dfrac{-\left(\sin x-\cos x\right)^{2}-\left(\sin x+\cos x\right)^{2}}{\left(\sin x-\cos x\right)^{2}} \\ \\ & =\dfrac{-\left[\sin ^{2} x+\cos ^{2} x-2 \sin x \cos x+\sin ^{2} x+\cos ^{2} x+2 \sin x \cos x\right]}{\left(\sin x-\cos x\right)^{2}} \\ \\ & =\dfrac{-\left[1+1\right]}{\left(\sin x-\cos x\right)^{2}} \\ \\ & =\dfrac{-2}{\left(\sin x-\cos x\right)^{2}} \end{aligned} $
18. $\dfrac{\sec x-1}{\sec x+1}$
उत्तर दिखाएं
Answer :
$\text{Let,}$
$f\left(x\right)=\dfrac{\sec x-1}{\sec x+1}$
$f\left(x\right)=\dfrac{\dfrac{1}{\cos x}-1}{\dfrac{1}{\cos x}+1}=\dfrac{1-\cos x}{1+\cos x}$
By quotient rule,
$ \begin{aligned} f^{\prime}\left(x\right) & =\dfrac{\left(1+\cos x\right) \dfrac{d}{d x}\left(1-\cos x\right)-\left(1-\cos x\right) \dfrac{d}{d x}\left(1+\cos x\right)}{\left(1+\cos x\right)^{2}} \\ \\ & =\dfrac{\left(1+\cos x\right)\left(\sin x\right)-\left(1-\cos x\right)\left(-\sin x\right)}{\left(1+\cos x\right)^{2}} \\ \\ & =\dfrac{\sin x+\cos x \sin x+\sin x-\sin x \cos x}{\left(1+\cos x\right)^{2}} \\ \\ & =\dfrac{2 \sin x}{\left(1+\cos x\right)^{2}} \\ \\ & =\dfrac{2 \sin x}{\left(1+\dfrac{1}{\sec x}\right)^{2}}=\dfrac{2 \sin x}{\dfrac{\left(\sec x+1\right)^{2}}{\sec ^{2} x}} \\ \\ & =\dfrac{2 \sin x \sec ^{2} x}{\left(\sec x+1\right)^{2}} \\ \\ & =\dfrac{\dfrac{2 \sin x}{\cos x} \sec x}{\left(\sec x+1\right)^{2}} \\ \\ & =\dfrac{2 \sec x \tan x}{\left(\sec x+1\right)^{2}} \end{aligned} $
19. $\sin ^{n} x$
उत्तर दिखाएं
Answer :
Let $y=\sin ^{n} x$.
Accordingly, for $n=1, y=\sin x$.
$\therefore \ \ \dfrac{d y}{d x}=\cos x$, i.e., $\dfrac{d}{d x} \sin x=\cos x$
For $n=2, y=\sin ^{2} x$.
$ \begin{aligned} \therefore \ \ \dfrac{d y}{d x} & =\dfrac{d}{d x}\left(\sin x \sin x\right) \\ \\
& =\left(\sin x\right)^{\prime} \sin x+\sin x\left(\sin x\right)^{\prime} \\ \\ & =\cos x \sin x+\sin x \cos x \\ \\ & =2 \sin x \cos x \qquad \ldots{(1)} \end{aligned} $
$ n=3, y=\sin ^{3} x $।
$ \begin{aligned} \therefore \ \ \dfrac{d y}{d x} & =\dfrac{d}{d x}\left(\sin x \sin ^{2} x\right) \\ \\ & =\left(\sin x\right)^{\prime} \sin ^{2} x+\sin x\left(\sin ^{2} x\right)^{\prime} \left[\text{ द्विगुणित उत्पाद नियम द्वारा }\right] \\ \\ & =\cos x \sin ^{2} x+\sin x\left(2 \sin x \cos x\right) \qquad \left[\text{ (1) का उपयोग करते हुए }\right] \\ \\ & =\cos x \sin ^{2} x+2 \sin ^{2} x \cos x & \\ \\ & =3 \sin ^{2} x \cos x & \end{aligned} $
हम दावा करते हैं कि $\dfrac{d}{d x}\left(\sin ^{n} x\right)=n \sin ^{\left(n-1\right)} x \cos x$
मान लीजिए कि हमारा दावा $n=k$ के लिए सत्य है।
अर्थात, $\dfrac{d}{d x}\left(\sin ^{k} x\right)=k \sin ^{\left(k-1\right)} x \cos x$
विचार करें
$ \begin{aligned} \dfrac{d}{d x}\left(\sin ^{k+1} x\right) & =\dfrac{d}{d x}\left(\sin x \sin ^{k} x\right) \\ \\ & =\left(\sin x\right)^{\prime} \sin ^{k} x+\sin x\left(\sin ^{k}\right)’ \\ \\ & =\cos x \sin ^{k} x+\sin x\left(k \sin ^{(k-1)}\right) \\ \\ & =\cos x \sin ^{k} x+k \sin ^{k} x \cos x \\ \\ & =\left(k+1\right) \sin ^{k} x \cos x \\ \\ & =\left(\sin x\right)^{\prime} \sin ^{k} x+\sin x\left(\sin ^{k} x\right)^{\prime} \qquad \left[\text{ द्विगुणित उत्पाद नियम द्वारा }\right] \\ \\ & =\cos x \sin ^{k} x+\sin x\left(k \sin ^{(k-1)} x \cos x\right) \qquad {\left[\text{ (2) का उपयोग करते हुए }\right]} \end{aligned} $
इस प्रकार, हमारा दावा $n=k+1$ के लिए सत्य है।
अतः, गणितीय आगमन द्वारा, $\dfrac{d}{d x}\left(\sin ^{n} x\right)=n \sin ^{\left(n-1\right)} x \cos x$
20. $\dfrac{a+b \sin x}{c+d \cos x}$
उत्तर दिखाएं
उत्तर :
मान लीजिए $f\left(x\right)=\dfrac{a+b \sin x}{c+d \cos x}$
भाग नियम द्वारा,
$
\begin{aligned}
f^{\prime}\left(x\right) & =\dfrac{\left(c+d \cos x\right) \dfrac{d}{d x}\left(a+b \sin x\right)-\left(a+b \sin x\right) \dfrac{d}{d x}\left(c+d \cos x\right)}{\left(c+d \cos x\right)^{2}} \\ \\
& =\dfrac{\left(c+d \cos x\right)\left(b \cos x\right)-\left(a+b \sin x\right)\left(-d \sin x\right)}{\left(c+d \cos x\right)^{2}} \\ \\ & =\dfrac{c b \cos x+b d \cos ^{2} x+a d \sin x+b d \sin ^{2} x}{\left(c+d \cos x\right)^{2}} \\ \\ & =\dfrac{b c \cos x+a d \sin x+b d\left(\cos ^{2} x+\sin ^{2} x\right)}{\left(c+d \cos x\right)^{2}} \\ \\ & =\dfrac{b c \cos x+a d \sin x+b d}{\left(c+d \cos x\right)^{2}} \end{aligned} $
21. $\dfrac{\sin \left(x+a\right)}{\cos x}$
उत्तर दिखाएं
Answer :
Let $f\left(x\right)=\dfrac{\sin \left(x+a\right)}{\cos x}$
By quotient rule,
$ \begin{aligned} f^{\prime}\left(x\right) & =\dfrac{\cos x \dfrac{d}{d x}\left[\sin \left(x+a\right)\right]-\sin \left(x+a\right) \dfrac{d}{d x} \cos x}{\cos ^{2} x} \\ \\ f^{\prime}\left(x\right) & =\dfrac{\cos x \dfrac{d}{d x}\left[\sin \left(x+a\right)\right]-\sin \left(x+a\right)\left(-\sin x\right)}{\cos ^{2} x} \qquad …{(i)} \end{aligned} $
Let $g\left(x\right)=\sin \left(x+a\right)$. Accordingly, $g\left(x+h\right)=\sin \left(x+h+a\right)$
By first principle,
$ \begin{aligned} g^{\prime}\left(x\right) & =\lim _ {h \to 0} \dfrac{g\left(x+h\right)-g\left(x\right)}{h} \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\sin \left(x+h+a\right)-\sin \left(x+a\right)\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[2 \cos \left(\dfrac{x+h+a+x+a}{2}\right) \sin \left(\dfrac{x+h+a-x-a}{2}\right)\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[2 \cos \left(\dfrac{2 x+2 a+h}{2}\right) \sin \left(\dfrac{h}{2}\right)\right] \\ \\ & =\lim _ {h \to 0}{ \cos \left( \dfrac { 2 x + 2 a + h } { 2 } \right) \left[\dfrac{\sin \left(\dfrac{h}{2}\right)}{\left(\dfrac{h}{2}\right)}\right]} \quad\left[\text{ As } h \to 0 \Rightarrow \dfrac{h}{2} \to 0\right] \\ \\ & =\lim _ {h \to 0} \cos \left(\dfrac{2 x+2 a+h}{2}\right) \lim _ {\frac{h}{2} \to 0}\left \lbrace \dfrac{\sin \left(\dfrac{h}{2}\right)}{\left(\dfrac{h}{2}\right)}\right \rbrace \quad\left[\lim _ {h \to 0} \dfrac{\sin h}{h}=1\right] \\ \\
& =\left(\cos \dfrac{2 x+2 a}{2}\right) \times 1 \\ \\ & =\cos \left(x+a\right) \qquad …{(ii)} \end{aligned} $
(1) और (2) से, हम प्राप्त करते हैं
$ \begin{aligned} f^{\prime}\left(x\right) & =\dfrac{\cos x \cdot \cos \left(x+a\right)+\sin x \sin \left(x+a\right)}{\cos ^{2} x} \\ \\ & =\dfrac{\cos \left(x+a-x\right)}{\cos ^{2} x} \\ \\ & =\dfrac{\cos a}{\cos ^{2} x} \end{aligned} $
22. $x^{4}\left(5 \sin x-3 \cos x\right)$
उत्तर दिखाएं
Answer :
मान लीजिए $f\left(x\right)=x^{4}\left(5 \sin x-3 \cos x\right)$
उत्पाद नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x\right) & =x^{4} \dfrac{d}{d x}\left(5 \sin x-3 \cos x\right)+\left(5 \sin x-3 \cos x\right) \dfrac{d}{d x}\left(x^{4}\right) \\ \\ & =x^{4}\left[5 \dfrac{d}{d x}\left(\sin x\right)-3 \dfrac{d}{d x}\left(\cos x\right)\right]+\left(5 \sin x-3 \cos x\right) \dfrac{d}{d x}\left(x^{4}\right) \\ \\ & =x^{4}\left[5 \cos x-3\left(-\sin x\right)\right]+\left(5 \sin x-3 \cos x\right)\left(4 x^{3}\right) \\ \\ & =x^{3}\left[5 x \cos x+3 x \sin x+20 \sin x-12 \cos x\right] \end{aligned} $
23. $\left(x^{2}+1\right) \cos x$
उत्तर दिखाएं
Answer:
मान लीजिए $f\left(x\right)=\left(x^{2}+1\right) \cos x$
उत्पाद नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x\right) & =\left(x^{2}+1\right) \dfrac{d}{d x}\left(\cos x\right)+\cos x \dfrac{d}{d x}\left(x^{2}+1\right) \\ \\ & =\left(x^{2}+1\right)\left(-\sin x\right)+\cos x\left(2 x\right) \\ \\ & =-x^{2} \sin x-\sin x+2 x \cos x \end{aligned} $
24. $\left(a x^{2}+\sin x\right)\left(p+q \cos x\right)$
उत्तर दिखाएं
Answer :
मान लीजिए $f\left(x\right)=\left(a x^{2}+\sin x\right)\left(p+q \cos x\right)$
उत्पाद नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x\right) & =\left(a x^{2}+\sin x\right) \dfrac{d}{d x}\left(p+q \cos x\right)+\left(p+q \cos x\right) \dfrac{d}{d x}\left(a x^{2}+\sin x\right) \\ \\ & =\left(a x^{2}+\sin x\right)\left(-q \sin x\right)+\left(p+q \cos x\right)\left(2 a x+\cos x\right) \\ \\
& =-q \sin x\left(a x^{2}+\sin x\right)+\left(p+q \cos x\right)\left(2 a x+\cos x\right) \end{aligned} $
25. $\left(x+\cos x\right)\left(x-\tan x\right)$
उत्तर दिखाएं
Answer :
मान लीजिए $f\left(x\right)=\left(x+\cos x\right)\left(x-\tan x\right)$
उत्पाद नियम के अनुसार,
$ \begin{aligned} f^{\prime}\left(x\right) & =\left(x+\cos x\right) \dfrac{d}{d x}\left(x-\tan x\right)+\left(x-\tan x\right) \dfrac{d}{d x}\left(x+\cos x\right) \\ \\ & =\left(x+\cos x\right)\left[\dfrac{d}{d x}\left(x\right)-\dfrac{d}{d x}\left(\tan x\right)\right]+\left(x-\tan x\right)\left(1-\sin x\right) \\ \\ & =\left(x+\cos x\right)\left[1-\dfrac{d}{d x} \tan x\right]+\left(x-\tan x\right)\left(1-\sin x\right)\qquad …(i) \\ \\ & \text{ मान लीजिए } g\left(x\right)=\tan x \text{। इस प्रकार, } g\left(x+h\right)=\tan \left(x+h\right) \end{aligned} $
प्रथम सिद्धांत के अनुसार,
$ \begin{aligned} g^{\prime}\left(x\right) & =\lim _ {h \to 0} \dfrac{g\left(x+h\right)-g\left(x\right)}{h} \\ \\ & =\lim _ {h \to 0}\left(\dfrac{\tan \left(x+h\right)-\tan x}{h}\right) \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x+h\right)}{\cos \left(x+h\right)}-\dfrac{\sin x}{\cos x}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x+h\right) \cos x-\sin x \cos \left(x+h\right)}{\cos \left(x+h\right) \cos x}\right] \\ \\ & =\dfrac{1}{\cos x} \cdot \lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x+h-x\right)}{\cos \left(x+h\right)}\right] \\ \\ & =\dfrac{1}{\cos x} \cdot \lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin h}{\cos \left(x+h\right)}\right] \\ \\ & =\dfrac{1}{\cos {x}} \cdot\left(\lim _ {h \to 0} \dfrac{\sin h}{h}\right) \cdot\left(\lim _ {h \to 0} \dfrac{1}{\cos \left(x+h\right)}\right) \\ \\ & =\dfrac{1}{\cos x} \times 1 \times \dfrac{1}{\cos \left(x+0\right)} \\ \\ & =\dfrac{1}{\cos ^{2} x} \\ \\ & =\sec ^{2} x \qquad … {(ii)} \end{aligned} $
इसलिए, (i) और (ii) से, हम प्राप्त करते हैं
$ \begin{aligned}
f^{\prime}\left(x\right) & =\left(x+\cos x\right)\left(1-\sec ^{2} x\right)+\left(x-\tan x\right)\left(1-\sin x\right) \\ \\ & =\left(x+\cos x\right)\left(-\tan ^{2} x\right)+\left(x-\tan x\right)\left(1-\sin x\right) \\ \\ & =-\tan ^{2} x\left(x+\cos x\right)+\left(x-\tan x\right)\left(1-\sin x\right) \end{aligned} $
26. $\dfrac{4 x+5 \sin x}{3 x+7 \cos x}$
उत्तर दिखाएं
Answer :
Let $f\left(x\right)=\dfrac{4 x+5 \sin x}{3 x+7 \cos x}$
By quotient rule,
$ \begin{aligned} f^{\prime}\left(x\right) & =\dfrac{\left(3 x+7 \cos x\right) \dfrac{d}{d x}\left(4 x+5 \sin x\right)-\left(4 x+5 \sin x\right) \dfrac{d}{d x}\left(3 x+7 \cos x\right)}{\left(3 x+7 \cos x\right)^{2}} \\ \\ & =\dfrac{\left(3 x+7 \cos x\right)\left[4 \dfrac{d}{d x}\left(x\right)+5 \dfrac{d}{d x}\left(\sin x\right)\right]-\left(4 x+5 \sin x\right)\left[3 \dfrac{d}{d x} (x)+7 \dfrac{d}{d x} \cos x\right]}{\left(3 x+7 \cos x\right)^{2}} \\ \\ & =\dfrac{\left(3 x+7 \cos x\right)\left(4+5 \cos x\right)-\left(4 x+5 \sin x\right)\left(3-7 \sin x\right)}{\left(3 x+7 \cos x\right)^{2}} \\ \\ & =\dfrac{12 x+15 x \cos x+28 \cos x+35 \cos ^{2} x-12 x+28 x \sin x-15 \sin x+35 \sin ^{2} x}{\left(3 x+7 \cos x\right)^{2}} \\ \\ & =\dfrac{15 x \cos x+28 \cos x+28 x \sin x-15 \sin x+35\left(\cos ^{2} x+\sin ^{2} x\right)}{\left(3 x+7 \cos x\right)^{2}} \\ \\ & =\dfrac{35+15 x \cos x+28 \cos x+28 x \sin x-15 \sin x}{\left(3 x+7 \cos x\right)^{2}} \end{aligned} $
27. $\dfrac{x^{2} \cos \left(\dfrac{\pi}{4}\right)}{\sin x}$
उत्तर दिखाएं
Answer :
Let $f\left(x\right)=\dfrac{x^{2} \cos \left(\dfrac{\pi}{4}\right)}{\sin x}$
By quotient rule,
$ \begin{aligned} f^{\prime}\left(x\right) & =\cos \dfrac{\pi}{4} \cdot\left[\dfrac{\sin x \dfrac{d}{d x}\left(x^{2}\right)-x^{2} \dfrac{d}{d x}\left(\sin x\right)}{\sin ^{2} x}\right] \\ \\ & =\cos \dfrac{\pi}{4} \cdot\left[\dfrac{\sin x \cdot 2 x-x^{2} \cos x}{\sin ^{2} x}\right] \\ \\
& =\dfrac{x \cos \dfrac{\pi}{4}\left[2 \sin x-x \cos x\right]}{\sin ^{2} x} \end{aligned} $
28. $\dfrac{x}{1+\tan x}$
उत्तर दिखाएं
Answer :
मान लीजिए $f\left(x\right)=\dfrac{x}{1+\tan x}$
$ \ f^{\prime}\left(x\right)=\dfrac{\left(1+\tan x\right) \dfrac{d}{d x}\left(x\right)-x \dfrac{d}{d x}\left(1+\tan x\right)}{\left(1+\tan x\right)^{2}}$
$f^{\prime}\left(x\right)=\dfrac{\left(1+\tan x\right)-x \cdot \dfrac{d}{d x}\left(1+\tan x\right)}{\left(1+\tan x\right)^{2}}\qquad …(i)$
मान लीजिए $g\left(x\right)=1+\tan x$. इस प्रकार, $g\left(x+h\right)=1+\tan \left(x+h\right)$.
प्रथम सिद्धांत से,
$ \begin{aligned} g^{\prime}\left(x\right) & =\lim _ {h \to 0} \dfrac{g\left(x+h\right)-g\left(x\right)}{h} \\ \\ & =\lim _ {h \to 0}\left[\dfrac{1+\tan \left(x+h\right)-1-\tan x}{h}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x+h\right)}{\cos \left(x+h\right)}-\dfrac{\sin x}{\cos x}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x+h\right) \cos x-\sin x \cos \left(x+h\right)}{\cos \left(x+h\right) \cos x}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x+h-x\right)}{\cos \left(x+h\right) \cos x}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin h}{\cos \left(x+h\right) \cos x}\right] \\ \\ & =\left(\lim _ {h \to 0} \dfrac{\sin h}{h}\right) \cdot\left(\lim _ {h \to 0} \dfrac{1}{\cos \left(x+h\right) \cos x}\right) \\ \\ & =1 \times \dfrac{1}{\cos ^{2} x}=\sec ^{2} x \\ \\ \Rightarrow \dfrac{d}{d x} & \left(1+\tan x\right)=\sec ^{2} x \qquad …{(ii)} \end{aligned} $
(1) और (2) से, हम प्राप्त करते हैं
$ f^{\prime}\left(x\right)=\dfrac{1+\tan x-x \sec ^{2} x}{\left(1+\tan x\right)^{2}} $
29. $\left(x+\sec x\right)\left(x-\tan x\right)$
उत्तर दिखाएं
Answer :
मान लीजिए $f\left(x\right)=\left(x+\sec x\right)\left(x-\tan x\right)$
उत्पाद नियम से,
$ \begin{aligned} f^{\prime}\left(x\right) & =\left(x+\sec x\right) \dfrac{d}{d x}\left(x-\tan x\right)+\left(x-\tan x\right) \dfrac{d}{d x}\left(x+\sec x\right) \\ \\
& =\left(x+\sec x\right)\left[\dfrac{d}{d x}\left(x\right)-\dfrac{d}{d x} \tan x\right]+\left(x-\tan x\right)\left[\dfrac{d}{d x}\left(x\right)+\dfrac{d}{d x} \sec x\right] \\ \\ & =\left(x+\sec x\right)\left[1-\dfrac{d}{d x} \tan x\right]+\left(x-\tan x\right)\left[1+\dfrac{d}{d x} \sec x\right] \qquad …{(i)} \end{aligned} $
मान लीजिए $f_1\left(x\right)=\tan x, f_2\left(x\right)=\sec x$
इस प्रकार, $f_1\left(x+h\right)=\tan \left(x+h\right)$ और $f_2\left(x+h\right)=\sec \left(x+h\right)$
$ \begin{aligned} f_1^{\prime}\left(x\right) & =\lim _ {h \to 0}\left(\dfrac{f_1\left(x+h\right)-f_1\left(x\right)}{h}\right) \\ \\ & =\lim _ {h \to 0}\left(\dfrac{\tan \left(x+h\right)-\tan x}{h}\right) \\ \\ & =\lim _ {h \to 0}\left[\dfrac{\tan \left(x+h\right)-\tan x}{h}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x+h\right)}{\cos \left(x+h\right)}-\dfrac{\sin x}{\cos x}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x+h\right) \cos x-\sin x \cos \left(x+h\right)}{\cos \left(x+h\right) \cos x}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin \left(x+h-x\right)}{\cos \left(x+h\right) \cos x}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\sin h}{\cos \left(x+h\right) \cos x}\right] \\ \\ & =\left(\lim _ {h \to 0} \dfrac{\sin h}{h}\right) \cdot\left(\lim _ {h \to 0} \dfrac{1}{\cos \left(x+h\right) \cos x}\right) \\ \\ & =1 \times \dfrac{1}{\cos ^{2} x}=\sec ^{2} x \\ \\ \Rightarrow \dfrac{d}{d x} & \tan x=\sec ^{2} x \qquad …{(ii)} \end{aligned} $
$ \begin{aligned} f_2^{\prime}\left(x\right) & =\lim _ {h \to 0}\left(\dfrac{f_2\left(x+h\right)-f_2\left(x\right)}{h}\right) \\ \\ & =\lim _ {h \to 0}\left(\dfrac{\sec \left(x+h\right)-\sec x}{h}\right) \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{1}{\cos \left(x+h\right)}-\dfrac{1}{\cos x}\right] \\ \\ & =\lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{\cos x-\cos \left(x+h\right)}{\cos \left(x+h\right) \cos x}\right] \\ \\
$$ \begin{aligned} & =\dfrac{1}{\cos x} \cdot \lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{-2 \sin \left(\dfrac{x+x+h}{2}\right) \cdot \sin \left(\dfrac{x-x-h}{2}\right)}{\cos \left(x+h\right)}\right] \\ \\ & =\dfrac{1}{\cos x} \cdot \lim _ {h \to 0} \dfrac{1}{h}\left[\dfrac{-2 \sin \left(\dfrac{2 x+h}{2}\right) \cdot \sin \left(\dfrac{-h}{2}\right)}{\cos \left(x+h\right)}\right] \\ \\ & =\dfrac{1}{\cos x} \cdot \lim _ {h \to 0}\left[\dfrac{\sin \left(\dfrac{2 x+h}{2}\right)\left \lbrace \dfrac{\sin \left(\frac{h}{2}\right)}{\frac{h}{2}}\right \rbrace }{\cos \left(x+h\right)}\right] \\ \\ & =\sec x \dfrac{\left \lbrace \lim _ {h \to 0} \sin \left(\dfrac{2 x+h}{2}\right)\right \rbrace \left \lbrace \lim _ {\frac{h}{2} \to 0} \dfrac{\sin \left(\frac{h}{2}\right)}{\frac{h}{2}}\right \rbrace }{\lim _ {h \to 0} \cos \left(x+h\right)} \\ \\ & =\sec x \cdot \dfrac{\sin x \cdot 1}{\cos x}\qquad …(iii) \\ \\ & \Rightarrow \dfrac{d}{d x} \sec x=\sec x \tan x \end{aligned} $$
समीकरण $(i), \ (ii),$ और $(iii)$ से, हम प्राप्त करते हैं
$f^{\prime}\left(x\right)=\left(x+\sec x\right)\left(1-\sec ^{2} x\right)+\left(x-\tan x\right)\left(1+\sec x \tan x\right)$
30. $\dfrac{x}{\sin ^{n} x}$
उत्तर दिखाएं
Answer :
मान लीजिए $f\left(x\right)=\dfrac{x}{\sin ^{n} x}$
भाग विधि के अनुसार,
$f^{\prime}\left(x\right)=\dfrac{\sin ^{n} x \dfrac{d}{d x} (x)-x \dfrac{d}{d x} \sin ^{n} x}{\sin ^{2 n} x}$
इसको आसानी से दिखाया जा सकता है कि $\dfrac{d}{d x} \sin ^{n} x=n \sin ^{n-1} x \cos x$
इसलिए,
$ \begin{aligned} f^{\prime}\left(x\right) & =\dfrac{\sin ^{n} x \dfrac{d}{d x} (x)-x \dfrac{d}{d x} \sin ^{n} x}{\sin ^{2 n} x} \\ \\ & =\dfrac{\sin ^{n} x \cdot 1-x\left(n \sin ^{n-1} x \cos x\right)}{\sin ^{2 n} x} \\ \\ & =\dfrac{\sin ^{n-1} x\left(\sin x-n x \cos x\right)}{\sin ^{2 n} x} \\ \\ & =\dfrac{\sin x-n x \cos x}{\sin ^{n+1} x} \end{aligned} $
सारांश
-
एक बिंदु के बाईं ओर के बिंदुओं द्वारा निर्धारित फ़ंक्शन के अपेक्षित मूल्य को उस बिंदु पर फ़ंक्शन के बाईं ओर सीमा कहते हैं। इसी तरह दाईं ओर सीमा भी।
-
एक फ़ंक्शन के एक बिंदु पर सीमा उस बिंदु पर बाईं ओर और दाईं ओर सीमा के सामान्य मूल्य होती है, यदि वे समान हों।
-
एक फ़ंक्शन $f$ और एक वास्तविक संख्या $a$ के लिए, $\lim\limits_{x \to a} f(x)$ और $f(a)$ समान नहीं हो सकते (वास्तव में, एक निर्धारित हो सकता है और दूसरा नहीं)।
-
फलन $f$ और $g$ के लिए निम्नलिखित सत्य है:
$ \begin{aligned} \qquad & \lim\limits_{x \to a}[f(x) \pm g(x)]=\lim\limits_{x \to a} f(x) \pm \lim\limits_{x \to a} g(x) \\ \\ & \lim\limits_{x \to a}[f(x) \cdot g(x)]=\lim\limits_{x \to a} f(x) \lim\limits_{x \to a} g(x) \\ \\ & \lim\limits_{x \to a}\left[\dfrac{f(x)}{g(x)}\right]=\dfrac{\lim\limits_{x \to a} f(x)}{\lim\limits_{x \to a} g(x)} \end{aligned} $
- निम्नलिखित कुछ मानक सीमाएँ हैं
$ \qquad \lim\limits_{x \to a} \dfrac{x^{n}-a^{n}}{x-a}=n a^{n-1} $
$
$ \qquad \begin{aligned} & \lim\limits_{x \to 0} \dfrac{\sin x}{x}=1 \\ & \lim\limits_{x \to 0} \dfrac{1-\cos x}{x}=0 \end{aligned} $
- किसी फलन $f$ के $a$ पर अवकलज को निम्नलिखित द्वारा परिभाषित किया जाता है
$ \qquad f^{\prime}(a)=\lim\limits_{h \to 0} \dfrac{f(a+h)-f(a)}{h} $
- किसी फलन $f$ के किसी बिंदु $x$ पर अवकलज को निम्नलिखित द्वारा परिभाषित किया जाता है
$ \qquad f^{\prime}(x)=\dfrac{d f(x)}{d x}=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h} $
- फलन $u$ और $v$ के लिए निम्नलिखित सत्य है:
$ \begin{aligned} \qquad & (u \pm v)^{\prime}=u^{\prime} \pm v^{\prime} \\
& (u v)^{\prime}=u^{\prime} v+u v^{\prime} \\ & \left(\dfrac{u}{v}\right)^{\prime}=\dfrac{u^{\prime} v-u v^{\prime}}{v^{2}} \text{ provided all are defined. } \end{aligned} $
- नीचे कुछ मानक अवकलज दिए गए हैं।
$ \begin{aligned} \qquad & \dfrac{d}{d x}(x^{n})=n x^{n-1} \\ & \dfrac{d}{d x}(\sin x)=\cos x \\ & \dfrac{d}{d x}(\cos x)=-\sin x \end{aligned} $
ऐतिहासिक टिप्पणी
गणित के इतिहास में दो नाम उल्लेखनीय हैं जो कलन के आविष्कार के लिए श्रेय विभाजित करते हैं, आइजैक न्यूटन (1642 - 1727) और जी. डब्ल्यू. लेब्निज़ (1646 - 1717)। दोनों ने सत्रहवीं सदी में आविष्कार के लिए स्वतंत्र रूप से कलन की खोज की। कलन के आगंतुक बनने के बाद कई गणितज्ञों ने कलन के आगे विकास के लिए योगदान दिया। गहरे अवधारणा के मुख्य रूप से बड़े गणितज्ञों के श्रेय है।
गणितज्ञ, A.L. कैउची, J.L. लग्रांज और कार्ल वेयरस्ट्रास। कैउची ने वर्तमान में हमारे पाठ्यपुस्तकों में सामान्य रूप से स्वीकृत कलन के आधार प्रस्तुत किया। कैउची ने फलन के अवकलज को परिभाषित करने के लिए ड’एलेम्बर्ट के सीमा के अवधारणा का उपयोग किया। सीमा की परिभाषा से शुरू करते हुए, कैउची ने $\alpha = 0$ के लिए $\dfrac{\sin \alpha}{\alpha}$ की सीमा जैसे उदाहरण दिए। उन्होंने $\dfrac{\Delta y}{\Delta x}=\dfrac{f(x+i)-f(x)}{i}$ लिखा, और $i \to 0$ के लिए सीमा को “फलन अवकलज” कहा, $y^{\prime}$ के रूप में $f^{\prime}(x)$ के लिए।
1900 से पहले यह माना जाता था कि कलन को बहुत कठिन शिक्षित किया जा सकता है। इसलिए कलन युवाओं के लिए पहुँच नहीं रहा था। लेकिन 1900 में जॉन परी और अंग्रेजी में अन्य लोगों ने दृष्टि फैलाई कि कलन के मूल विचार और विधियाँ सरल हैं और वे विद्यालयों में भी शिक्षित किए जा सकते हैं। एफएल ग्रिफिन ने पहले वर्ष के छात्रों के लिए कलन की शिक्षा के शुरुआती अध्ययन की शुरुआत की। इसे उस समय के लिए एक बहुत धीरे अध्ययन के रूप में देखा गया था।
आज न केवल गणित बल्कि भौतिक विज्ञान, रसायन विज्ञान, अर्थशास्त्र और जैविक विज्ञान जैसे कई अन्य विषय भी कलन के फलों का आनंद ले रहे हैं।





