अध्याय 11 तीन आयामी ज्यामिति का परिचय
गणित विज्ञान की राजकोई और श्रमिक कन्या है - E.T. BELL
11.1 परिचय
आप याद कर सकते हैं कि एक तल में एक बिंदु की स्थिति को निर्धारित करने के लिए, हमें तल में एक दूसरे के लंबकर्ता रेखाओं के दो प्रतिच्छेदी रेखाएँ चाहिए। इन रेखाओं को निर्देशांक अक्ष कहते हैं और दो संख्याओं को बिंदु के संदर्भ में अक्षों के संबंध में निर्देशांक कहते हैं। वास्तविक जीवन में, हमें केवल तल में स्थित बिंदुओं के साथ काम करने की आवश्यकता नहीं होती। उदाहरण के लिए, अंतरिक्ष में फेंके गए गेंद के विभिन्न समय बिंदुओं पर स्थिति या एक विमान के उड़ान भरते समय एक स्थान से दूसरे स्थान तक उड़ते समय विभिन्िमान के विभिन्न समय बिंदुओं पर स्थिति की विचार करें।

लेओनहार्ड यूलर (1707-1783)
इसी तरह, यदि हम एक कमरे के छत से लटके एक बल्ब के सबसे निचले छोर की स्थिति या कमरे के छत के ब्लैड फैन के केंद्रीय छोर की स्थिति ज्ञात करना चाहें, तो हमें केवल कमरे के दो लंबकर्ता दीवारों से बिंदु की लंबवत दूरी के साथ-साथ कमरे के फर्श से बिंदु की ऊंचाई की भी आवश्यकता होगी। अतः हमें केवल दो बल्कि तीन संख्याएं आवश्यक होंगी, जो बिंदु की तीन लंबवत दूरियों को निरूपित करती होंगी, जो तीन आपस में लंबवत तलों से बिंदु की दूरी होंगी, अर्थात कमरे के फर्श और दो संलग्न दीवारों से। तीन दूरियों को निरूपित करने वाली तीन संख्याएं बिंदु के तीन निर्देशांक कहलाती हैं, जो तीन निर्देशांक तलों के संदर्भ में बिंदु के निर्देशांक होते हैं। अतः अंतरिक्ष में एक बिंदु के तीन निर्देशांक होते हैं। इस अध्याय में हम तीन आयामी अंतरिक्ष में ज्यामिति के मूल संसाधनों के अध्ययन करेंगे।*
11.2 तीन आयामी अंतरिक निर्देशांक अक्ष एवं निर्देशांक समतल
तीन समतलों को एक बिंदु $O$ पर प्रतिच्छेदित होते हैं जैसे कि ये तीन समतल एक दूसरे के साथ परस्पर लंब हों (चित्र 11.1)। इन तीन समतलों के प्रतिच्छेदन रेखाएँ $X^{\prime} OX, Y^{\prime} OY$ और $Z^{\prime} OZ$ होती हैं, जिन्हें क्रमशः $x, y$ और $z$-अक्ष कहा जाता है। हम ध्यान दें कि ये रेखाएँ एक दूसरे के साथ परस्पर लंब होती हैं। ये रेखाएँ आयताकार निर्देशांक प्रणाली का निर्माण करती हैं। XOY, YOZ और ZOX समतल, क्रमशः XY-समतल, YZ-समतल और ZX-समतल कहलाते हैं, जिन्हें तीन निर्देशांक समतल कहा जाता है। हम XOY समतल को कागज के तल के रूप में ले लेते हैं और रेखा $Z^{\prime} OZ$ को XOY समतल के लंब के रूप में ले लेते हैं।

चित्र 11.1
यदि कागज के तल को स्थानीय मान लिया जाए, तो रेखा $Z^{\prime} OZ$ ऊर्ध्वाधर होगी। XY-तल से ऊपर की दिशा में $OZ$ के अनुदिश मापी गई दूरियाँ धनात्मक मानी जाती हैं और नीचे की दिशा में $OZ^{\prime}$ के अनुदिश मापी गई दूरियाँ ऋणात्मक मानी जाती हैं। इसी तरह, $ZX$-तल के दाहिने ओर $OY$ के अनुदिश मापी गई दूरियाँ धनात्मक मानी जाती हैं, $ZX$-तल के बाईं ओर और $O Y^{\prime}$ के अनुदिश मापी गई दूरियाँ ऋणात्मक मानी जाती हैं, YZ-तल के सामने $O X$ के अनुदिश मापी गई दूरियाँ धनात्मक मानी जाती हैं और इसके पीछे $OX^{\prime}$ के अनुदिश मापी गई दूरियाँ ऋणात्मक मानी जाती हैं। बिंदु $O$ को निर्देशांक प्रणाली के मूल बिंदु कहा जाता है। तीन निर्देशांक तल अंतरिक अंशों के आठ भागों में बाँटते हैं जिन्हें अष्टांश कहते हैं। इन अष्टांशों को $XOYZ, X^{\prime} OYZ, X^{\prime} OY Y, XOY ’ Z, XOYZ$, $X^{\prime} OYZ, X^{\prime} OY^{\prime} Z^{\prime}$ और $XOY^{\prime} Z^{\prime}$ के रूप में नाम दिया जा सकता है और उन्हें क्रमशः I, II, III, …, VIII के रूप में दर्शाया जाता है।
11.3 अंतरिक्ष में बिंदु के निर्देशांक
अंतरिक्ष में एक निश्चित निर्देशांक प्रणाली का चयन कर लेने के बाद, जो निर्देशांक अक्ष, निर्देशांक तल और मूल बिंदु से बना होता है, अब हम बताएंगे कि अंतरिक्ष में एक बिंदु दिये गए होने पर, हम उस बिंदु के तीन निर्देशांक $(x, y, z)$ कैसे संबंधित करते हैं और विपरीत, तीन संख्याओं के एक त्रिक $(x, y, z)$ दिये गए होने पर, हम अंतरिक्ष में एक बिंदु कैसे निर्धारित करते हैं।

चित्र 11.2
एक बिंदु $P$ अंतरिक अंतराल में दिया गया है, हम एक $\mathbf{X}$ लंब PM को XY-समतल पर गिराते हैं, जहां M इस लंब का पाद होता है (चित्र 11.2)। फिर, बिंदु M से हम $x$-अक्ष के लंब रेखा ML खींचते हैं, जो इसे बिंदु L पर मिलती है। मान लीजिए OL के बराबर $x$, LM के बराबर $y$ और MP के बराबर $z$ है। तब $x$, $y$ और $z$ को बिंदु $P$ के अंतरिक अंतराल में $x$, $y$ और $z$ निर्देशांक कहा जाता है। चित्र 11.2 में हम ध्यान दें सकते हैं कि बिंदु $P(x, y, z)$ XOYZ अक्ष के आठवाँ चतुर्थांश में स्थित है और इसलिए सभी $x$, $y$ और $z$ धनात्मक हैं। यदि $P$ कोई अन्य आठवाँ चतुर्थांश में होता, तो $x$, $y$ और $z$ के चिन्ह बदल जाते।
अत: प्रत्येक बिंदु $P$ अंतरिक अंतराल में एक क्रमित त्रिक $(x, y, z)$ के वास्तविक संख्याओं के संगत होता है।
विपरीत रूप से, किसी भी त्रिक $(x, y, z)$ दिया गया हो, तो हम सबसे पहले $x$-अक्ष पर $x$ के संगत बिंदु $L$ निर्धारित करेंगे, फिर $XY$-समतल में ऐसा बिंदु $M$ ज्ञात करेंगे जहां $(x, y)$, $M$ के $XY$-समतल में निर्देशांक हों। ध्यान दें कि $LM$, $x$-अक्ष के लंबवत है या $y$-अक्ष के समानांतर है। $M$ तक पहुंचे बाद, हम $XY$-समतल के लंबवत एक लंब $MP$ खींचेंगे और इस पर $z$ के संगत बिंदु $P$ निर्धारित करेंगे। इस प्रकार प्राप्त बिंदु $P$ के निर्देशांक $(x, y, z)$ होते हैं। अतः अंतरिक अंतराल में बिंदुओं और वास्तविक संख्याओं के क्रमित त्रिक $(x, y, z)$ के बीच एक एक-एक संगति होती है।
अथवा, अंतरिक अंतराल में बिंदु $P$ से, हम तीन तल खींचते हैं जो निर्देशांक तलों के समानांतर हों, जो $x$-अक्ष, $y$-अक्ष और $z$-अक्ष को क्रमशः $A, B$ और $C$ बिंदुओं पर मिलते हैं (चित्र 11.3)। मान लीजिए $OA=x, OB=y$ और $OC=z$। तब, बिंदु $P$ के निर्देशांक $x, y$ और $z$ होंगे और हम लिखते हैं $P(x, y, z)$। विपरीत, दिए गए $x, y$ और $z$ के लिए, हम तीन निर्देशांक अक्षों पर तीन बिंदुओं $A, B$ और $C$ को स्थापित करते हैं। बिंदुओं $A, B$ और $C$ से हम क्रमशः YZ-तल, ZX-तल और XY-तल के समानांतर तल खींचते हैं।

इन तीन तलों, अर्थात, ADPF, BDPE और CEPF के प्रतिच्छेदन बिंदु, स्पष्ट रूप से बिंदु $P$ है, जो क्रमवाचक त्रिक $(x, y, z)$ के संगत है। हम देखते हैं कि यदि $P(x, y, z)$ अंतरिक अंतराल में कोई बिंदु है, तो $x, y$ और $z$ क्रमशः YZ, ZX और XY तलों से लंब दूरी हैं।
नोट - मूल बिंदु $O$ के निर्देशांक $(0,0,0)$ हैं। $x$-अक्ष पर किसी भी बिंदु के निर्देशांक $(x, 0,0)$ होंगे और YZ-तल में किसी भी बिंदु के निर्देशांक $(0, y, z)$ होंगे।
टिप्पणी एक बिंदु के निर्देशांक के चिह्न बताते हैं कि बिंदु किस अष्टांश में स्थित है। नीचे दिया गया तालिका आठ अष्टांशों में निर्देशांक के चिह्नों को दिखाती है।
तालिका 11.1
$ \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline \text{अष्टांश/निर्देशांक} & \text{I} & \text{II} & \text{III} & \text{IV} & \text{V} & \text{VI} & \text{VII} & \text{VIII} \\ \hline x & + & - & - & + & + & - & - & + \\ \hline y & + & + & - & - & + & + & - & - \\ \hline z & + & + & + & + & - & - & - & - \\
\hline \end{array} $
उदाहरण 1 आकृति 11.3 में, यदि $P$ बिंदु $(2,4,5)$ है, तो $F$ के निर्देशांक ज्ञात कीजिए।
हल बिंदु $F$ के लिए, OY के अनुदिश मापी गई दूरी शून्य है। अतः $F$ के निर्देशांक $(2,0,5)$ हैं।
उदाहरण 2 बिंदु $(-3,1,2)$ और $(-3,1,-2)$ किस आठवीं चतुर्भुज में स्थित हैं?
हल सारणी 11.1 से, बिंदु $(-3,1,2)$ दूसरे आठवीं चतुर्भुज में और बिंदु $(-3,1,-2)$ आठवीं चतुर्भुज VI में स्थित है।
अभ्यास 11.1
1. एक बिंदु $x$-अक्ष पर है। इसके $y$-निर्देशांक और $z$-निर्देशांक क्या होंगे?
उत्तर दिखाएं
उत्तर :
यदि एक बिंदु $x$-अक्ष पर है, तो इसके $y$-निर्देशांक और $z$-निर्देशांक शून्य होंगे।
2. एक बिंदु $XZ$-समतल में है। इसके $y$-निर्देशांक के बारे में आप क्या कह सकते हैं?
उत्तर दिखाएं
उत्तर :
यदि एक बिंदु $XZ$ समतल में है, तो इसके $y$-निर्देशांक शून्य होंगे।
3. निम्नलिखित बिंदुओं के अष्टांश कौन-कौन से हैं:
$ \begin{aligned} & (1,2,3),(4,-2,3),(4,-2,-5),(4,2,-5),(-4,2,-5),(-4,2,5),(-3,-1,6)(-2,-4,-7) . \end{aligned} $
उत्तर दिखाएं
उत्तर :
बिंदु $(1,2,3)$ के $x$-निर्देशांक, $y$-निर्देशांक और $z$-निर्देशांक सभी धनात्मक हैं। अतः यह अष्टांश $\mathbf{I}$ में स्थित है।
बिंदु $(4,-2,3)$ के $x$-निर्देशांक, $y$-निर्देशांक और $z$-निर्देशांक क्रमशः धनात्मक, ऋणात्मक और धनात्मक हैं। अतः यह अष्टांश $IV$ में स्थित है।
बिंदु $(4,-2,-5)$ के $x$-निर्देशांक, $y$-निर्देशांक और $z$-निर्देशांक क्रमशः धनात्मक, ऋणात्मक और ऋणात्मक हैं। अतः यह अष्टांश $VIII$ में स्थित है।
बिंदु $(4,2,-5)$ के $x$-निर्देशांक, $y$-निर्देशांक और $z$-निर्देशांक क्रमशः धनात्मक, धनात्मक और ऋणात्मक हैं। अतः यह अष्टांश $\mathbf{V}$ में स्थित है।
बिंदु $(-4,2,-5)$ के $x$-निर्देशांक, $y$-निर्देशांक और $z$-निर्देशांक क्रमशः ऋणात्मक, धनात्मक और ऋणात्मक हैं। अतः यह अष्टांश $VI$ में स्थित है।
बिंदु $(-4,2,5)$ के $x$-निर्देशांक, $y$-निर्देशांक और $z$-निर्देशांक क्रमशः ऋणात्मक, धनात्मक और धनात्मक हैं। अतः यह अष्टांश $II$ में स्थित है।
बिंदु $(-3,-1,6)$ के $x$-निर्देशांक, $y$-निर्देशांक और $z$-निर्देशांक क्रमशः ऋणात्मक, ऋणात्मक और धनात्मक हैं। अतः यह अष्टांश $III$ में स्थित है।
बिंदु $(2,-4,-7)$ के $x$-निर्देशांक, $y$-निर्देशांक और $z$-निर्देशांक क्रमशः धनात्मक, ऋणात्मक और ऋणात्मक हैं। अतः, यह बिंदु आठवाँ आकृति में स्थित है।
4. रिक्त स्थान भरें:
(i) $x$-अक्ष और $y$-अक्ष के संयोजन द्वारा निर्धारित समतल को ____________ कहते हैं
(ii) XY-समतल में बिंदुओं के निर्देशांक ___________ के रूप में होते हैं
(iii) निर्देशांक समतल अंतरिक्ष को ___________ आकृतियों में विभाजित करते हैं।
उत्तर दिखाएं
Answer :
(i) $XY-$ समतल
(ii) $(x, y, 0)$
(3) $\text{ Eight }$
11.4 दो बिंदुओं के बीच दूरी
हमने दो-आयामी निर्देशांक प्रणाली में दो बिंदुओं के बीच दूरी के बारे में अध्ययन किया है। अब हम इस अध्ययन को तीन-आयामी प्रणाली में विस्तारित करेंगे।
मान लीजिए $P(x_1, y_1, z_1)$ और $Q(x_2, y_2, z_2)$ एक आयतीय निर्देशांक प्रणाली $OX, OY$ और $OZ$ के संदर्भ में दो बिंदु हैं। बिंदुओं $P$ और $Q$ से होकर निर्देशांक तलों के समानांतर तल खींचें ताकि एक आयतीय समांतर चतुष्फलक बने जिसका एक विकर्ण PQ हो (चित्र 11.4)।

अब, क्योंकि $\angle PAQ$ एक समकोण $\quad \mathbf{X}$ कोण है, इसलिए त्रिभुज PAQ में,
$ PQ^{2}=PA^{2}+AQ^{2} \quad\quad\quad\quad\quad\quad\quad \ldots(1) $
इसके अतिरिक्त, त्रिभुज ANQ एक समकोण त्रिभुज है जिसमें $\angle ANQ$ एक समकोण है।
इसलिए $\quad\quad\quad AQ^{2}=AN^{ 2}+NQ^{2} \quad\quad\quad\quad\quad\quad\quad \ldots(2)$
(1) और (2) से, हम प्राप्त करते हैं
$ \mathrm{PQ}^{2}=\mathrm{PA}^{2}+\mathrm{AN}^{2}+\mathrm{NQ}^{2} $
अब $\quad\quad\quad\mathrm{PA}=y _{2}-y _{1}, \mathrm{AN}=x _{2}-x _{1}$ और $\mathrm{NQ}=z _{2}-z _{1}$
इसलिए $\quad\quad\quad\mathrm{PQ}^{2}=\left(x _{2}-x _{1}\right)^{2}+\left(y _{2}-y _{1}\right)^{2}+\left(z _{2}-z _{1}\right)^{2}$
इसलिए $\quad\quad\quad PQ=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}}$
यह हमें दो बिंदुओं $(x_1, y_1, z_1)$ और $(x_2, y_2, z_2)$ के बीच दूरी देता है।
विशेष रूप से, यदि $x_1=y_1=z_1=0$, अर्थात, बिंदु $P$ मूल बिंदु $O$ है, तो $OQ=\sqrt{x_2{ }^{2}+y_2{ }^{2}+z_2{ }^{2}}$, जो मूल बिंदु $O$ और किसी भी बिंदु $Q(x_2, y_2, z_2)$ के बीच दूरी देता है।
उदाहरण 3 बिंदु $P(1,-3,4)$ और $Q(-4,1,2)$ के बीच की दूरी ज्ञात कीजिए।
हल बिंदु $P(1,-3,4)$ और $Q(-4,1,2)$ के बीच दूरी PQ है
$ \begin{aligned} PQ & =\sqrt{(-4-1)^{2}+(1+3)^{2}+(2-4)^{2}} \\ & =\sqrt{25+16+4} \\ & =\sqrt{45}=3 \sqrt{5} \text{ इकाई } \end{aligned} $
उदाहरण 4 दिखाइए कि बिंदु $P(-2,3,5)$, $Q(1,2,3)$ और $R(7,0,-1)$ संरेख हैं।
हल हम जानते हैं कि बिंदु संरेख कहलाते हैं यदि वे एक रेखा पर स्थित हो।
अब, $\qquad P Q=\sqrt{(1+2)^{2}+(2-3)^{2}+(3-5)^{2}}=\sqrt{9+1+4}=\sqrt{14}$
$Q R=\sqrt{(7-1)^{2}+(0-2)^{2}+(-1-3)^{2}}=\sqrt{36+4+16}=\sqrt{56}=2 \sqrt{14}$
और $ \qquad P R=\sqrt{(7+2)^{2}+(0-3)^{2}+(-1-5)^{2}}=\sqrt{81+9+36}=\sqrt{126}=3 \sqrt{14} $
इस प्रकार, $PQ+QR=PR$। अतः, $P, Q$ और $R$ संरेख हैं।
उदाहरण 5 बिंदु A $(3,6,9), B(10,20,30)$ और C $(25,-41,5)$, एक समकोण त्रिकोण के शीर्ष हैं?
हल दूरी सूत्र के अनुसार, हम निम्नलिखित प्राप्त करते हैं
$ \begin{aligned} AB^{2} & =(10-3)^{2}+(20-6)^{2}+(30-9)^{2} \\ & =49+196+441=686 \\ BC^{2} & =(25-10)^{2}+(-41-20)^{2}+(5-30)^{2} \\ $
& =225+3721+625=4571 \end{aligned} $
$ \begin{aligned} CA^{2} & =(3-25)^{2}+(6+41)^{2}+(9-5)^{2} \\ & =484+2209+16=270 \end{aligned} $
हम देखते हैं कि $\quad \quad\quad CA^{2}+AB^{2} \neq BC^{2}$.
इसलिए, त्रिभुज $ABC$ समकोण त्रिभुज नहीं है।
उदाहरण 6 ऐसे बिंदुओं $P$ के समुच्चय का समीकरण ज्ञात कीजिए जिसके लिए $PA^{2}+PB^{2}=2 k^{2}$, जहाँ $A$ और $B$ क्रमशः $(3,4,5)$ और $(-1,3,-7)$ बिंदु हैं।
हल मान लीजिए बिंदु $P$ के निर्देशांक $(x, y, z)$ हैं।
यहाँ $PA^{2}=(x-3)^{2}+(y-4)^{2}+(z-5)^{2}$
$\qquad PB^{2}=(x+1)^{2}+(y-3)^{2}+(z+7)^{2}$
दिए गए शर्त के अनुसार $PA^{2}+PB^{2}=2 k^{2}$, हमें प्राप्त होता है
$ (x-3)^{2}+(y-4)^{2}+(z-5)^{2}+(x+1)^{2}+(y-3)^{2}+(z+7)^{2}=2 k^{2} \\ \text{ अर्थात, } \quad 2 x^{2}+2 y^{2}+2 z^{2}-4 x-14 y+4 z=2 k^{2}-109 . $
अभ्यास 11.2
1. निम्नलिखित बिंदु युग्मों के बीच की दूरी ज्ञात कीजिए:
(i) $(2,3,5)$ और $(4,3,1)$
(ii) $(-3,7,2)$ और $(2,4,-1)$
(iii) $(-1,3,-4)$ और $(1,-3,4)$
(iv) $(2,-1,3)$ और $(-2,1,3)$।
उत्तर दिखाएं
उत्तर :
बिंदु $P(x_1, y_1, z_1)$ और $P(x_2, y_2, z_2)$ के बीच की दूरी दी गई है
(i) बिंदु $(2,3,5)$ और $(4,3,1)$ के बीच की दूरी
$=\sqrt{(4-2)^{2}+(3-3)^{2}+(1-5)^{2}}$
$=\sqrt{(2)^{2}+(0)^{2}+(-4)^{2}}$
$=\sqrt{4+16}$
$=\sqrt{20}$
$=2 \sqrt{5}$
(ii) बिंदु $(-3, 7, 2)$ और $(2, 4, -1)$ के बीच की दूरी
$=\sqrt{(2+3)^{2}+(4-7)^{2}+(-1-2)^{2}}$
$=\sqrt{(5)^{2}+(-3)^{2}+(-3)^{2}}$
$=\sqrt{25+9+9}$
$=\sqrt{43}$
(iii) बिंदु $(-1, 3, -4)$ और $(1, -3, 4)$ के बीच की दूरी
$=\sqrt{(1+1)^{2}+(-3-3)^{2}+(4+4)^{2}}$
$=\sqrt{(2)^{2}+(-6)^{3}+(8)^{2}}$
$=\sqrt{4+36+64}=\sqrt{104}=2 \sqrt{26}$
(iv) बिंदु $(2, -1,3)$ और $(-2, 1, 3)$ के बीच की दूरी
$=\sqrt{(-2-2)^{2}+(1+1)^{2}+(3-3)^{2}}$
$=\sqrt{(-4)^{2}+(2)^{2}+(0)^{2}}$
$=\sqrt{16+4}$
$=\sqrt{20}$
$=2 \sqrt{5}$
2. दिखाइए कि बिंदु $(-2,3,5),(1,2,3)$ और $(7,0,-1)$ संरेख हैं।
उत्तर दिखाएं
उत्तर :
मान लीजिए बिंदु $(-2, 3, 5), \ (1, 2, 3),$ और $(7, 0, -1)$ को क्रमशः $P, Q,$ और $R$ से निरूपित किया गया है।
बिंदु $P, Q$, और $R$ संरेख होंगे यदि वे एक रेखा पर स्थित हों।
$ \begin{aligned} PQ & =\sqrt{(1+2)^{2}+(2-3)^{2}+(3-5)^{2}} \\ \\ & =\sqrt{(3)^{2}+(-1)^{2}+(-2)^{2}} \\ \\ & =\sqrt{9+1+4} \\ \\ & =\sqrt{14} \\ \\ QR & =\sqrt{(7-1)^{2}+(0-2)^{2}+(-1-3)^{2}} \\ \\ & =\sqrt{(6)^{2}+(-2)^{2}+(-4)^{2}} \\ \\ & =\sqrt{36+4+16} \\ \\ & =\sqrt{56} \\ \\ & =2 \sqrt{14} \end{aligned} $
$ \begin{aligned} P R= & \sqrt{(7+2)^{2}+(0-3)^{2}+(-1-5)^{2}} \\ \\ & =\sqrt{(9)^{2}+(-3)^{2}+(-6)^{2}} \\ \\ & =\sqrt{81+9+36} \\ \\ & =\sqrt{126} \\ \\
& =3 \sqrt{14} \end{aligned} $
यहाँ, $PQ+QR=\sqrt{14}+2 \sqrt{14}=3 \sqrt{14}=PR$
इसलिए, बिंदु $P(- 2,3,5), Q(1,2,3)$, और $R(7,0, - 1 )$ संरेख हैं।
3. निम्नलिखित की जांच करें:
(i) $(0,7,-10),(1,6,-6)$ और $(4,9,-6)$ एक समद्विबाहु त्रिभुज के शीर्ष हैं।
(ii) $(0,7,10),(-1,6,6)$ और $(-4,9,6)$ एक समकोण त्रिभुज के शीर्ष हैं।
(iii) $(-1,2,1),(1,-2,5),(4,-7,8)$ और $(2,-3,4)$ एक समांतर चतुर्भुज के शीर्ष हैं।
उत्तर दिखाएं
उत्तर :
(i) मान लीजिए बिंदु $(0,7, -10), \ (1, 6, - 6 ),$ और $(4, 9, -6)$ क्रमशः $A, \ B,$ और $C$ द्वारा नोट किए गए हैं।
$ \begin{aligned} AB & =\sqrt{(1-0)^{2}+(6-7)^{2}+(-6+10)^{2}} \\ \\ & =\sqrt{(1)^{2}+(-1)^{2}+(4)^{2}} \\ \\ & =\sqrt{1+1+16} \\ \\ & =\sqrt{18} \\ \\ & =3 \sqrt{2} \\ \\ BC & =\sqrt{(4-1)^{2}+(9-6)^{2}+(-6+6)^{2}} \\ \\ & =\sqrt{(3)^{2}+(3)^{2}} \\ \\ & =\sqrt{9+9}=\sqrt{18}=3 \sqrt{2} \\ \\ CA & =\sqrt{(0-4)^{2}+(7-9)^{2}+(-10+6)^{2}} \\ \\ & =\sqrt{(-4)^{2}+(-2)^{2}+(-4)^{2}} \\ \\ & =\sqrt{16+4+16}=\sqrt{36}=6 \end{aligned} $
यहाँ, $A B=B C \neq C A$
इसलिए, दिए गए बिंदु एक समद्विबाहु त्रिभुज के शीर्ष हैं।
(ii) मान लीजिए $(0,7,10), \ (-1, 6, 6),$ और $(- 4,9,6 )$ क्रमशः $A, \ B,$ और $C$ द्वारा नोट किए गए हैं।
$ \begin{aligned} AB & =\sqrt{(-1-0)^{2}+(6-7)^{2}+(6-10)^{2}} \\ \\ & =\sqrt{(-1)^{2}+(-1)^{2}+(-4)^{2}} \\ \\ & =\sqrt{1+1+16}=\sqrt{18} \\ \\ & =3 \sqrt{2} \\ \\ BC & =\sqrt{(-4+1)^{2}+(9-6)^{2}+(6-6)^{2}} \\ \\ & =\sqrt{(-3)^{2}+(3)^{2}+(0)^{2}} \\ \\ & =\sqrt{9+9}=\sqrt{18} \\ \\ & =3 \sqrt{2} \end{aligned} $
$ \begin{aligned} CA & =\sqrt{(0+4)^{2}+(7-9)^{2}+(10-6)^{2}} \\ \\ & =\sqrt{(4)^{2}+(-2)^{2}+(4)^{2}} \\ \\ & =\sqrt{16+4+16} \\ \\ & =\sqrt{36} \\ \\ & =6 \end{aligned} $
अब, $AB^{2}+BC^{2}=(3 \sqrt{2})^{2}+(3 \sqrt{2})^{2}=18+18=36=AC^{2}$
इसलिए, पाइथागोरस प्रमेय के अनुसार, $A B C$ एक समकोण त्रिभुज है।
इसलिए, दिए गए बिंदु एक समकोण त्रिभुज के शीर्ष हैं।
(iii) मान लीजिए $(-1,2,1), \ (1, - 2,5), \ (4, - 7,8),$ और $(2, - 3,4)$ क्रमशः $A, B, C$, और $D$ द्वारा नोट किए गए हैं।
$ \begin{aligned} AB & =\sqrt{(1+1)^{2}+(-2-2)^{2}+(5-1)^{2}} \\ \\ & =\sqrt{4+16+16} \\ \\ & =\sqrt{36} \\ \\ & =6 \end{aligned} $
$ \begin{aligned} BC & =\sqrt{(4-1)^{2}+(-7+2)^{2}+(8-5)^{2}} \\ \\ & =\sqrt{9+25+9}=\sqrt{43} \\ \\ CD & =\sqrt{(2-4)^{2}+(-3+7)^{2}+(4-8)^{2}} \\ \\ & =\sqrt{4+16+16} \\ \\ & =\sqrt{36} \\ \\ & =6 \end{aligned} $
$ \begin{aligned} DA & =\sqrt{(-1-2)^{2}+(2+3)^{2}+(1-4)^{2}} \\ \\ & =\sqrt{9+25+9}=\sqrt{43} \end{aligned} $
यहाँ, $A B=C D=6, \ B C=A D=\sqrt{43}$
इसलिए, चतुर्भुज $A B C D$ के विपरीत भुजाएँ बराबर हैं, जिनके शीर्ष क्रमशः लिए गए हैं।
अतः, $A B C D$ एक समांतर चतुर्भुज है।
इसलिए, दिए गए बिंदु एक समांतर चतुर्भुज के शीर्ष हैं।
4. बिंदुओं $(1,2,3)$ और $(3,2,-1)$ से समान दूरी पर स्थित बिंदुओं के समुच्चय का समीकरण ज्ञात कीजिए।
उत्तर दिखाएं
उत्तर :
मान लीजिए $P(x, y, z)$ वह बिंदु है जो बिंदुओं $A(1,2,3)$ और $B(3,2, - 1)$ से समान दूरी पर है।
इसलिए, $PA = PB$
$\Rightarrow \ \ PA^{2}=PB^{2}$
$\Rightarrow \ \ (x-1)^{2}+(y-2)^{2}+(z-3)^{2}=(x-3)^{2}+(y-2)^{2}+(z+1)^{2}$
$ x^2-2x+1 +y^2 - 4y +4 + z^2-6z+9 = x^2 -6x+9 + y^2 - 4y +4 +z^2 +2z+1 $
$\Rightarrow \ \ - 2 x - 4 y - 6 z+14=- 6 x - 4 y+2 z+14$
$\Rightarrow \ \ - 2 x - 6 z+6 x - 2 z=0$
$\Rightarrow \ \ 4 x - 8 z=0$
$\Rightarrow \ \ x - 2 z=0$
अतः, अभीष्ट समीकरण $x - 2 z=0$ है।
5. बिंदु $P$ के ऐसे समुच्चय का समीकरण ज्ञात कीजिए जिसकी दूरी $A(4,0,0)$ और $B(-4,0,0)$ से जोड़े गए बिंदुओं के योग 10 हो।
उत्तर दिखाएं
उत्तर :
मान लीजिए $P$ के निर्देशांक $(x, y, z)$ हैं।
बिंदुओं $A$ और $B$ के निर्देशांक क्रमशः $(4,0,0)$ और $(-4,0,0)$ हैं।
दिया गया है कि $PA+PB=10$।
$ \begin{aligned} & \Rightarrow \ \ \sqrt{(x-4)^{2}+y^{2}+z^{2}}+\sqrt{(x+4)^{2}+y^{2}+z^{2}}=10 \\ \\
$$ \Rightarrow \ \ \sqrt{(x-4)^{2}+y^{2}+z^{2}}=10-\sqrt{(x+4)^{2}+y^{2}+z^{2}} $$ $$ \end{aligned} $$
$
उपर दिए गए समीकरण के दोनों तरफ वर्ग करने पर हम प्राप्त करते हैं
$ \begin{aligned} & \Rightarrow \ \ (x-4)^{2}+y^{2}+z^{2}=100-20 \sqrt{(x+4)^{2}+y^{2}+z^{2}}+(x+4)^{2}+y^{2}+(z)^{2} \\ \\ & \Rightarrow \ \ x^{2}-8 x+16+y^{2}+z^{2}=100-20 \sqrt{x^{2}+8 x+16+y^{2}+z^{2}}+x^{2}+8 x+16+y^{2}+z^{2} \\ \\ & \Rightarrow \ \ 20 \sqrt{x^{2}+8 x+16+y^{2}+z^{2}}=100+16 x \\ \\ & \Rightarrow \ \ 5 \sqrt{x^{2}+8 x+16+y^{2}+z^{2}}=(25+4 x) \end{aligned} $$
$
उपर दिए गए समीकरण के दोनों तरफ वर्ग करने पर हम प्राप्त करते हैं
$25(x^{2}+8 x+16+y^{2}+z^{2})=625+16 x^{2}+200 x$
$\Rightarrow \ \ 25 x^{2}+200 x+400+25 y^{2}+25 z^{2}=625+16 x^{2}+200 x$
$\Rightarrow \ \ 9 x^{2}+25 y^{2}+25 z^{2} - 225=0$
इसलिए, आवश्यक समीकरण $9 x^{2}+25 y^{2}+25 z^{2} - 225=0$ है।
विविध उदाहरण
उदाहरण 7 सिद्ध कीजिए कि बिंदु A $(1,2,3)$, B (-1, -2, -1), C (2, 3, 2) और $D(4,7,6)$ एक समांतर चतुर्भुज $ABCD$ के शीर्ष हैं, लेकिन यह एक आयत नहीं है।
हल ABCD के समांतर चतुर्भुज होने को दिखाने के लिए हमें विपरीत भुजाओं के बराबर होने को दिखाना होगा। ध्यान दें।
$ \begin{aligned} & AB=\sqrt{(-1-1)^{2}+(-2-2)^{2}+(-1-3)^{2}}=\sqrt{4+16+16}=6 \\ & BC=\sqrt{(2+1)^{2}+(3+2)^{2}+(2+1)^{2}}=\sqrt{9+25+9}=\sqrt{43} \\ & CD=\sqrt{(4-2)^{2}+(7-3)^{2}+(6-2)^{2}}=\sqrt{4+16+16}=6 \\ & DA=\sqrt{(1-4)^{2}+(2-7)^{2}+(3-6)^{2}}=\sqrt{9+25+9}=\sqrt{43} \end{aligned} $
क्योंकि $A B=C D$ और $B C=A D, A B C D$ एक समांतर चतुर्भुज है।
अब, हमें दिखाना है कि $ABCD$ एक आयत नहीं है। इसके लिए हम दिखाएंगे कि विकर्ण $AC$ और $BD$ बराबर नहीं हैं। हमारे पास है:
$ \begin{aligned} & AC=\sqrt{(2-1)^{2}+(3-2)^{2}+(2-3)^{2}}=\sqrt{1+1+1}=\sqrt{3} \\ & BD \quad=\sqrt{(4+1)^{2}+(7+2)^{2}+(6+1)^{2}}=\sqrt{25+81+49}=\sqrt{155} . \end{aligned} $
क्योंकि $A C \neq B D, A B C D$ एक आयत नहीं है।
नोट - हम एक गुण का उपयोग करके भी दिखा सकते हैं कि $ABCD$ एक समांतर चतुर्भुज है, जिसके विकर्ण $AC$ और $BD$ एक दूसरे को समद्विभाजित करते हैं।
उदाहरण 8 बिंदुओं $A(3,4,-5)$ और $B(-2,1,4)$ से बराबर दूरी वाले बिंदुओं $P$ के समुच्चय का समीकरण ज्ञात कीजिए।
हल यदि $P(x, y, z)$ कोई भी बिंदु हो जैसे कि $PA=PB$ हो।
अब $\sqrt{(x-3)^{2}+(y-4)^{2}+(z+5)^{2}} = \sqrt{(x+2)^{2}+(y-1)^{2}+(z-4)^{2}}$
या $\quad\quad (x-3)^{2}+(y-4)^{2}+(z+5)^{2}=(x+2)^{2}+(y-1)^{2}+(z-4)^{2}$
या $\quad \quad 10 x+6 y-18 z-29=0$.
उदाहरण 9 त्रिभुज $ABC$ के केंद्रक बिंदु $(1,1,1)$ पर है। यदि $A$ और $B$ के निर्देशांक क्रमशः $(3,-5,7)$ और $(-1,7,-6)$ हैं, तो बिंदु $C$ के निर्देशांक ज्ञात कीजिए।
हल मान लीजिए $C$ के निर्देशांक $(x, y, z)$ हैं और केंद्रक $G$ के निर्देशांक $(1,1,1)$ हैं। तब
$\dfrac{x+3-1}{3}=1$, अर्थात् $x=1$ $\dfrac{y-5+7}{3}=1, \text { अर्थात् } y=1$ $\dfrac{z+7-6}{3}=1, \text { अर्थात् } z=2.$
इसलिए, $C$ के निर्देशांक $(1,1,2)$ हैं।
अध्याय 11 पर अतिरिक्त अभ्यास
1. एक समांतर चतुर्भुज $ABCD$ के तीन शीर्ष $A\left(3,-1,2\right), \ B \left(1,2,-4\right)$ और $C\left(-1,1,2\right)$ दिए गए हैं। चौथे शीर्ष के निर्देशांक ज्ञात कीजिए।
उत्तर दिखाएं
उत्तर :
एक समांतर चतुर्भुज $A B C D$ के तीन शीर्ष $ A\left(3, - 1, 2 \right), B\left(1,2,- 4\right),$ और $C \left(-1, 1, 2\right).$ चौथे शीर्ष के निर्देशांक $D\left(x, y, z\right)$ हों।
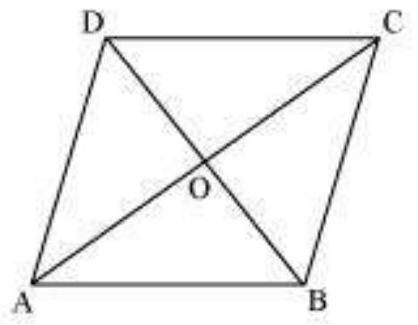
हम जानते हैं कि समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।
इसलिए, समांतर चतुर्भुज $A B C D$ में $A C$ और $B D$ एक दूसरे को समद्विभाजित करते हैं।
$\therefore \ \ $ $A C$ का मध्य-बिंदु = $B D$ का मध्य-बिंदु
$\Rightarrow \ \ \left(\dfrac{3-1}{2}, \dfrac{-1+1}{2}, \dfrac{2+2}{2}\right)=\left(\dfrac{x+1}{2}, \dfrac{y+2}{2}, \dfrac{z-4}{2}\right)$
$\Rightarrow \ \ \left(1,0,2\right)=\left(\dfrac{x+1}{2}, \dfrac{y+2}{2}, \dfrac{z-4}{2}\right)$
$\Rightarrow \ \ \dfrac{x+1}{2}=1, \dfrac{y+2}{2}=0$, और $\dfrac{z-4}{2}=2$
$\Rightarrow \ \ x=1, y=- 2$ , और $z=8$
इसलिए, चौथे शीर्ष के निर्देशांक $\left(1, -2, 8\right)$ हैं।
2. त्रिभुज के शीर्ष $A\left(0,0,6\right), B\left(0,4,0\right)$ और $\left(6,0,0\right)$ के लिए माध्यिकाओं की लंबाई ज्ञात कीजिए।
उत्तर दिखाएं
उत्तर :
मान लीजिए $A D, B E$, और $C F$ दिए गए त्रिभुज $A B C$ की माध्यिकाएं हैं।
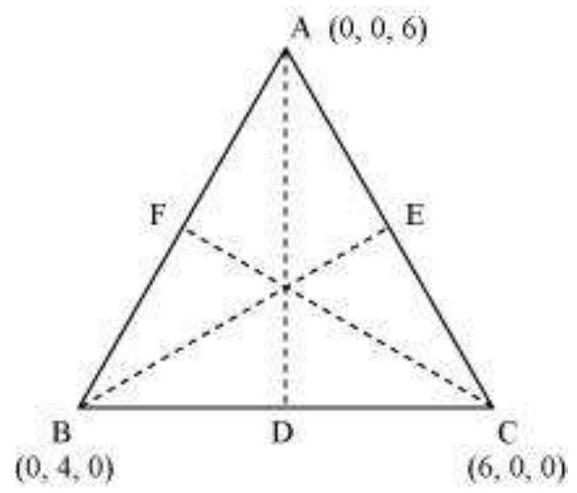
क्योंकि $A D$ माध्यिका है, तो $D$ बिंदु $B C$ का मध्य-बिंदु है।
$\therefore \ \ $ बिंदु $D$ के निर्देशांक $\left(\dfrac{0+6}{2}, \dfrac{4+0}{2}, \dfrac{0+0}{2}\right)=\left(3,2,0\right)$
$AD=\sqrt{\left(0-3\right)^{2}+\left(0-2\right)^{2}+\left(6-0\right)^{2}}=\sqrt{9+4+36}=\sqrt{49}=7$
क्योंकि $BE$ माध्यिका है, $E$ $AC$ का मध्य-बिंदु है।
$\therefore \ \ $ बिंदु $E$ के निर्देशांक $\left(\dfrac{0+6}{2}, \dfrac{0+0}{2}, \dfrac{6+0}{2}\right)=\left(3,0,3\right)$
$BE=\sqrt{\left(3-0\right)^{2}+\left(0-4\right)^{2}+\left(3-0\right)^{2}}=\sqrt{9+16+9}=\sqrt{34}$
क्योंकि $CF$ माध्यिका है, $F$ $AB$ का मध्य-बिंदु है।
$\therefore \ \ $ बिंदु $F$ के निर्देशांक $\left(\dfrac{0+0}{2}, \dfrac{0+4}{2}, \dfrac{6+0}{2}\right)=\left(0,2,3\right)$
$CF$ की लंबाई $\sqrt{\left(6-0\right)^{2}+\left(0-2\right)^{2}+\left(0-3\right)^{2}}=\sqrt{36+4+9}=\sqrt{49}=7$
इस प्रकार, $\triangle ABC$ की माध्यिकाओं की लंबाई $7, \sqrt{34}$, और $7$ है।
3. यदि त्रिभुज $PQR$ के शीर्ष $P\left(2 a, 2,6\right)$, $Q\left(-4,3 b,-10\right)$ और $R\left(8,14,2 c\right)$ के लिए मूल बिंदु त्रिभुज $PQR$ का केंद्रक है, तो $a, b$ और $c$ के मान ज्ञात कीजिए।
उत्तर दिखाएं
Answer :
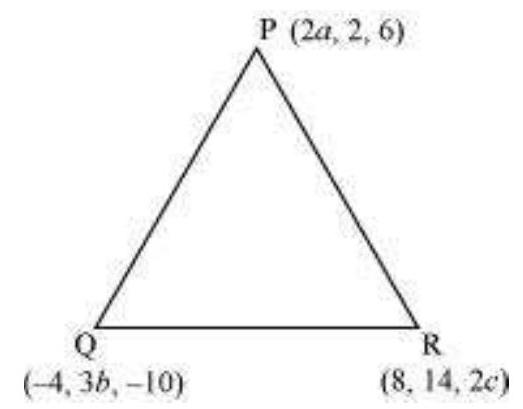
यह ज्ञात है कि त्रिभुज के शीर्ष $\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)$ और $\left(x_3, y_3, z_3\right)$ के लिए केंद्रक के निर्देशांक $\left(\dfrac{x_1+x_2+x_3}{3}, \dfrac{y_1+y_2+y_3}{3}, \dfrac{z_1+z_2+z_3}{3}\right)$ होते हैं।
इसलिए, $\Delta PQR$ के केंद्रक के निर्देशांक $\left(\dfrac{2 a-4+8}{3}, \dfrac{2+3 b+14}{3}, \dfrac{6-10+2 c}{3}\right)=\left(\dfrac{2 a+4}{3}, \dfrac{3 b+16}{3}, \dfrac{2 c-4}{3}\right)$
यह दिया गया है कि मूल बिंदु त्रिभुज $PQR$ का केंद्रक है।
$\therefore \ \ \left(0,0,0\right)=\left(\dfrac{2 a+4}{3}, \dfrac{3 b+16}{3}, \dfrac{2 c-4}{3}\right)$
$\Rightarrow \ \ \dfrac{2 a+4}{3}=0, \dfrac{3 b+16}{3}=0$ और $\dfrac{2 c-4}{3}=0$
$\Rightarrow \ \ a=-2, b=-\dfrac{16}{3}$ और $c=2$
इस प्रकार, $a, b$, और $c$ के संगत मान हैं
$ -2,-\dfrac{16}{3}, \text{ और } 2 $
4. यदि $A$ और $B$ क्रमशः बिंदु $\left(3,4,5\right)$ और $\left(-1,3,-7\right)$ हों, तो उन बिंदुओं $P$ के समुच्चय के समीकरण ज्ञात कीजिए जहाँ $PA^{2}+PB^{2}=k^{2}$, जहाँ $k$ एक स्थिरांक है।
उत्तर दिखाएं
उत्तर :
बिंदुओं $A$ और $B$ के निर्देशांक क्रमशः $\left(3,4,5\right)$ और $(-1,3,-7)$ दिए गए हैं।
मान लीजिए बिंदु $P$ के निर्देशांक $\left(x, y, z\right)$ हैं।
दूरी सूत्र का उपयोग करते हुए, हम प्राप्त करते हैं
$ \begin{aligned} PA^{2} & =\left(x-3\right)^{2}+\left(y-4\right)^{2}+\left(z-5\right)^{2} \\ \\ & =x^{2}+9-6 x+y^{2}+16-8 y+z^{2}+25-10 z \\ \\ & =x^{2}-6 x+y^{2}-8 y+z^{2}-10 z+50 \\ \\ PB^{2} & =\left(x+1\right)^{2}+\left(y-3\right)^{2}+\left(z+7\right)^{2} \\ \\ & =x^{2}+2 x+y^{2}-6 y+z^{2}+14 z+59 \end{aligned} $
अब, यदि $PA^{2}+PB^{2}=k^{2}$,
तो,
$ \begin{aligned} & \left(x^{2}-6 x+y^{2}-8 y+z^{2}-10 z+50\right)+\left(x^{2}+2 x+y^{2}-6 y+z^{2}+14 z+59\right)=k^{2} \\ \\ & \Rightarrow \ \ 2 x^{2}+2 y^{2}+2 z^{2}-4 x-14 y+4 z+109=k^{2} \\ \\ & \Rightarrow \ \ 2\left(x^{2}+y^{2}+z^{2}-2 x-7 y+2 z\right)=k^{2}-109 \\ \\ & \Rightarrow \ \ x^{2}+y^{2}+z^{2}-2 x-7 y+2 z=\dfrac{k^{2}-109}{2} \\ \\ & \qquad x^{2}+y^{2}+z^{2}-2 x-7 y+2 z=\dfrac{k^{2}-109}{2} . \end{aligned} $
सारांश
-
तीन आयामों में, आयतनी द्विआधारी निर्देशांक प्रणाली के निर्देश अक्ष तीन आपस में लंबवत रेखाएँ होती हैं। इन अक्षों को $x$, $y$ और $z$-अक्ष कहते हैं।
-
अक्षों के जोड़े द्वारा निर्धारित तीन तल निर्देशांक तल होते हैं, जिन्हें XY, YZ और ZX-तल कहते हैं।
-
तीन निर्देशांक तल स्थान को आठ भागों में बांटते हैं, जिन्हें अष्टांश कहते हैं।
-
तीन आयामी ज्यामिति में एक बिंदु $P$ के निर्देशांक हमेसा $(x, y, z)$ के त्रिक रूप में लिखे जाते हैं। यहाँ $x, y$ और $z$ YZ, ZX और XY-तलों से दूरी होते हैं।
-
(i) कोई भी बिंदु $x$-अक्ष पर $(x, 0,0)$ के रूप में होता है
$\qquad$ (ii) कोई भी बिंदु $y$-अक्ष पर $(0, y, 0)$ के रूप में होता है
$\qquad$ (iii) $z$-अक्ष पर कोई भी बिंदु $(0,0, z)$ के रूप का होता है।
- दो बिंदुओं $P(x_1, y_1, z_1)$ और $Q(x_2, y_2, z_2)$ के बीच दूरी निम्नलिखित द्वारा दी जाती है
$ \qquad PQ=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}} $
ऐतिहासिक टिप्पणी
रेने डेकार्ट (1596-1650), विश्लेषणात्मक ज्यामिति के पिता, 1637 में केवल तल ज्यामिति के साथ ही सीमित रहे। उसी तरह उनके सह-विकसितक बर्नार्ड फर्माट (1601-1665) और ला हिर (1640-1718) के कार्य में भी तल ज्यामिति के बारे में ही बात की गई। यद्यपि उनके कार्यों में तीन आयामी निर्देशांक ज्यामिति के लिए सुझाव देखे जा सकते हैं लेकिन विस्तारित विवरण नहीं है। डेकार्ट के पास तीन आयामी निर्देशांक के विचार थे लेकिन उन्होंने इसे विकसित नहीं किया। जे. बर्नूली (1667-1748) ने 1715 में लीबनिज को एक पत्र में आधुनिक तीन निर्देशांक तलों की अवधारणा प्रस्तुत की। यह आधुनिक तीन निर्देशांक तलों की अवधारणा आधुनिक ज्यामिति में उपयोग की जाती है। यह आधुनिक तीन आयामी विश्लेषणात्मक ज्यामिति के लिए पहली बार एक लेख में आधुनिक फ्रांसीसी अकादमी में प्रस्तुत करने वाले एंटोनिन पेरेंट (1666-1716) द्वारा विस्तार से विकसित की गई।
L.Euler (1707-1783) ने 1748 में अपनी “ज्यामिति का परिचय” के द्वितीय आवृत्ति के अनुसरण में अनुबंध के अध्याय 5 में तीन आयामी निर्देशांक ज्यामिति के व्यवस्थित अध्ययन को शुरू किया।
तीन से अधिक आयामों में ज्यामिति के विस्तार तकनीक निम्नलिखित आधुनिक शताब्दी के मध्य तक नहीं हुआ, जिसका प्रसिद्ध अनुप्रयोग आइंस्टीन के सापेक्षता के सिद्धांत में स्पेस-टाइम के अवकाश में है।





