अध्याय 10 दीर्घवृत्तीय खंड
आपके छात्रों के लिए ज्ञान के वास्तविक जीवन से संबंध काफी स्पष्ट हो जाए और उन्हें समझ आए कि ज्ञान के माध्यम से दुनिया कैसे बदली जा सकती है। - बर्ट्रैंड रसेल
10.1 परिचय
पिछले अध्याय 10 में, हमने एक रेखा के समीकरण के विभिन्न रूपों के बारे में अध्ययन किया है। इस अध्याय में, हम कुछ अन्य वक्रों के बारे में अध्ययन करेंगे, जैसे कि वृत्त, दीर्घवृत्त, परवलय और हाइपरबोला। परवलय और हाइपरबोला के नाम अपोलोनियस द्वारा दिए गए हैं। ये वक्र वास्तव में दीर्घवृत्तीय खंड या अधिक सामान्य रूप से दीर्घवृत्त के रूप में जाने जाते हैं क्योंकि वे एक समतल के एक दोलन वाले समकोण वृत्तीय शंकु के साथ कटाव के रूप में प्राप्त किए जा सकते हैं। ये वक्र ग्रहगति, टेलीस्कोप और एंटीना के डिज़ाइन, फ़लाशलाइट और ऑटोमोबाइल हेडलाइट में प्रतिबिंबक आदि जैसे क्षेत्रों में बहुत व्यापक अनुप्रयोग हैं।

अपोलोनियस (262 ईसा पूर्व -190 ईसा पूर्व)
अब, आगामी अनुच्छेदों में हम देखेंगे कि एक तल किस प्रकार एक द्विगुणित नापेड़ अपरिवर्ती वृत्तीय शंकु के साथ प्रतिच्छेदन विभिन्न प्रकार के वक्रों के निर्माण करता है।
10.2 शंकु के प्रतिच्छेदन
मान लीजिए $l$ एक निश्चित ऊर्ध्वाधर रेखा है और $m$ एक अन्य रेखा है जो इस रेखा $l$ के एक निश्चित बिंदु $V$ पर प्रतिच्छेद करती है और इस रेखा $l$ के साथ कोण $\alpha$ पर झुकी हुई है (चित्र 10.1)।

चित्र 10.1
मान लीजिए हम रेखा $m$ को रेखा $l$ के चारों ओर इस प्रकार घुमाते हैं कि कोण $\alpha$ स्थिर रहे। तो उत्पन्न सतह एक दो नाप वाला समकोण शंकु होगा, जिसे अब आगे शंकु के रूप में संदर्भित किया जाएगा और यह दोनों दिशाओं में अनंत तक फैला होगा (चित्र 10.2)।

चित्र 10.2
बिंदु $V$ को शीर्ष कहते हैं; रेखा $l$ को शंकु के अक्ष कहते हैं। घूमती हुई रेखा $m$ को शंकु का एक उत्पादक कहते हैं। शीर्ष शंकु को दो भागों में विभाजित करता है, जिन्हें नैप्पेस कहते हैं।
यदि हम एक समतल के शंकु के साथ प्रतिच्छेदन लें, तो प्राप्त अनुछेद को एक दीर्घवृत्तीय अनुछेद कहते हैं। इस प्रकार, दीर्घवृत्तीय अनुछेद वे वक्र होते हैं जो एक समतल द्वारा एक सीधे वृत्तीय शंकु के प्रतिच्छेदन से प्राप्त किए जाते हैं।
हम शंकु के साथ प्रतिच्छेदन करने वाले समतल के स्थिति के अनुसार और शंकु के ऊर्ध्वाधर अक्ष के सापेक्ष इसके कोण के अनुसार विभिन्न प्रकार के दीर्घवृत्तीय अनुछेद प्राप्त कर सकते हैं। मान लीजिए $\beta$ वह कोण है जो प्रतिच्छेदन करने वाले समतल द्वारा शंकु के ऊर्ध्वाधर अक्ष के साथ बनाया गया है (चित्र 10.3)।
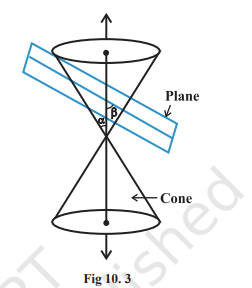
समतल के शंकु के शीर्ष या शीर्ष के नीचे या ऊपर के किसी भी भाग पर काट लेने पर उसके छेद के आकार अलग-अलग हो सकते हैं।
10.2.1 वृत्त, एलिप्स, परबोला और हाइपरबोला
जब समतल शंकु के शीर्ष के अलावा उसके नापे को काटता है, तो हमें निम्नलिखित स्थितियाँ मिलती हैं:
(a) जब $\beta=90^{\circ}$, तो छेद एक वृत्त होता है (चित्र 10.4)।

चित्र 10.4
(b) जब $\alpha<\beta<90^{\circ}$, तो अनुछेद एक अतिपरवलय होता है (चित्र 10.5)।

चित्र 10.5
(c) जब $\beta=\alpha$; तो अनुछेद एक परवलय होता है (चित्र 10.6)।

चित्र 10.6
(ऊपर के तीन स्थितियों में से प्रत्येक में, समतल शंकु के एक नापे के पूरी तरह से ऊपर बाजू काटता है।)
(d) जब $0 \leq \beta<\alpha$; समतल दोनों नापों के माध्यम से गुजरता है और प्रतिच्छेदन वक्र एक परवलय होता है (चित्र 10.7)।

चित्र 10.7
10.2.2 अपसामान्य शंकु परिच्छेद
जब समतल शंकु के शीर्ष पर काटता है, तो हमें निम्नलिखित विभिन्न मामले मिलते हैं:
(a) जब $\alpha<\beta \leq 90^{\circ}$, तो परिच्छेद एक बिंदु होता है (चित्र 10.8)।

चित्र 10.8
(b) जब $\beta=\alpha$, तो समतल शंकु के एक उत्पादक को समावेश करता है और परिच्छेद एक सीधी रेखा होती है (चित्र 10.9)।

चित्र 10.9
यह एक परवलय के अपस्थिति अवस्था का मामला है।
(c) जब $0 \leq \beta<\alpha$, तो अनुछेद एक एक दूसरे को प्रतिच्छेद करने वाली सीधी रेखाओं के युग्म के रूप में होता है (चित्र 10.10)। यह एक हाइपरबोला के अपस्थिति अवस्था का मामला है।

चित्र 10.8 (a)

चित्र 10.8 (b)
निम्नलिखित अनुच्छेदों में, हम इन परिच्छेदों के समीकरणों को उनके ज्यामितीय गुणों के आधार पर मानक रूप में प्राप्त करेंगे।
10.3 वृत्त
परिभाषा 1 एक वृत्त एक तल में स्थित सभी बिंदुओं का समुच्चय होता है जो एक निश्चित बिंदु से समान दूरी पर होते हैं।
स्थिर बिंदु को वृत्त केंद्र कहते हैं और केंद्र से वृत्त पर किसी बिंदु की दूरी को वृत्त की त्रिज्या कहते हैं (चित्र 10.11)।

चित्र 10.11
यदि वृत्त केंद्र मूल बिंदु पर हो, तो वृत्त के समीकरण के रूप से सबसे आसान होता है। हालांकि, हम नीचे एक दिए गए केंद्र और त्रिज्या वाले वृत्त के समीकरण का निर्माण करेंगे (चित्र 10.12)।

चित्र 10.12
मान लीजिए $C(h, k)$ वृत्त केंद्र हो और $r$ त्रिज्या हो। मान लीजिए $P(x, y)$ वृत्त पर कोई बिंदु हो (चित्र 10.12)। तब, परिभाषा के अनुसार, $|CP| = r$ होता है। दूरी सूत्र के अनुसार, हमें निम्न प्राप्त होता है
$\sqrt{(x-h)^{2}+(y-k)^{2}}=r$
अर्थात $\quad(x-h)^{2}+(y-k)^{2}=r^{3}$
यह वृत्त के अभीष्ट समीकरण है जिसका केंद्र $(h, k)$ और त्रिज्या $r$ है।
उदाहरण 1 केंद्र $(0,0)$ और त्रिज्या $r$ वाले वृत्त का समीकरण ज्ञात कीजिए।
हल यहाँ $h=k=0$ है। अतः वृत्त का समीकरण $x^{2}+y^{2}=r^{2}$ है।
उदाहरण 2 केंद्र $(-3,2)$ और त्रिज्या 4 वाले वृत्त का समीकरण ज्ञात कीजिए।
हल यहाँ $h=-3, k=2$ और $r=4$ है। अतः अभीष्ट वृत्त का समीकरण है
$ (x+3)^{2}+(y-2)^{2}=16 $
उदाहरण 3 वृत्त $x^{2}+y^{2}+8 x+10 y-8=0$ के केंद्र और त्रिज्या ज्ञात कीजिए।
हल दिया गया समीकरण है
उदाहरण 1 केंद्र $(0,0)$ और त्रिज्या $r$ वाले वृत्त का समीकरण ज्ञात कीजिए।
हल यहाँ $h=k=0$ है। अतः वृत्त का समीकरण $x^{2}+y^{2}=r^{2}$ है।
उदाहरण 2 केंद्र $(-3,2)$ और त्रिज्या 4 वाले वृत्त का समीकरण ज्ञात कीजिए।
हल यहाँ $h=-3, k=2$ और $r=4$ है। अतः अभीष्ट वृत्त का समीकरण है
$ (x+3)^{2}+(y-2)^{2}=16 $
उदाहरण 3 वृत्त $x^{2}+y^{2}+8 x+10 y-8=0$ के केंद्र और त्रिज्या ज्ञात कीजिए।
हल दिया गया समीकरण है
$ (x^{2}+8 x)+(y^{2}+10 y)=8 $
अब, बराबरी के चिह्न के अंदर वर्ग पूर्ण करते हुए, हमें प्राप्त होता है
$ (x^{2}+8 x+16)+(y^{2}+10 y+25)=8+16+2 $
अर्थात $ \qquad (x+4)^{2}+(y+5)^{2}=49 $
अर्थात $\qquad [x-(-4)]^2 + [y-(-5)]^2 = 7^2$
इसलिए, दी गई वृत्त केंद्र $(-4,-5)$ पर है और त्रिज्या 7 है ।
उदाहरण 4 वृत्त का समीकरण ज्ञात कीजिए जो बिंदुओं $(2,-2)$ और $(3,4)$ से गुजरता है और जिसका केंद्र रेखा $x+y=2$ पर स्थित हो।
हल मान लीजिए वृत्त का समीकरण $(x-h)^{2}+(y-k)^{2}=r^{2}$ है।
चूंकि वृत्त बिंदु $(2,-2)$ और $(3,4)$ से गुजरता है, हमें है
$ \begin{aligned} (2-h)^{2}+(-2-k)^{2}=r^{2} \qquad \ldots \text{(1)} \end{aligned} $
और $ \begin{aligned} (3-h)^{2}+(4-k)^{2}=r^{2}\qquad \ldots \text{(2)} \end{aligned} $
इसके अलावा, केंद्र रेखा $x+y=2$ पर स्थित है, इसलिए हमें है
$ \begin{aligned} h+k=2 \qquad \ldots \text{(3)} \end{aligned} $
समीकरण (1), (2) और (3) को हल करने पर हमें प्राप्त होता है
$ h=0.7, \quad k=1.3 \text{ और } r^{2}=12.58 $
इसलिए, अभीष्ट वृत्त का समीकरण है
$ (x-0.7)^{2}+(y-1.3)^{2}=12.58 . $
EXERCISE 10.1
निम्नलिखित प्रत्येक अभ्यास $1$ से $5$ में, केंद्र के साथ वृत्त का समीकरण ज्ञात कीजिए
1. केंद्र $\left(0,2\right)$ और त्रिज्या $2$
उत्तर दिखाएं
उत्तर :
केंद्र $\left(h, k\right)$ और त्रिज्या $r$ वाले एक वृत्त का समीकरण निम्नलिखित होता है
$\left(x-h\right)^{2}+\left(y-k\right)^{2}=r^{2}$
दिया गया है कि केंद्र $\left(h, k\right)=\left(0,2\right)$ और त्रिज्या $\left(r\right)=2$
इसलिए, वृत्त का समीकरण है
$\left(x-0\right)^{2}+\left(y-2\right)^{2}=2^{2}$
$x^{2}+y^{2}+4-4 y=4$
$x^{2}+y^{2}-4 y=0$
2. केंद्र $\left(-2,3\right)$ और त्रिज्या $4$
उत्तर दिखाएं
उत्तर :
केंद्र $\left(h, k\right)$ और त्रिज्या $r$ वाले एक वृत्त का समीकरण निम्नलिखित होता है
$\left(x-h\right)^{2}+\left(y-k\right)^{2}=r^{2}$
दिया गया है कि केंद्र $\left(h, k\right)=\left(-2,3\right)$ और त्रिज्या $\left(r\right)=4$
इसलिए, वृत्त का समीकरण है
$\left(x+2\right)^{2}+\left(y-3\right)^{2}=\left(4\right)^{2}$
$x^{2}+4 x+4+y^{2}-6 y+9=16$
$x^{2}+y^{2}+4 x-6 y-3=0$
3. केंद्र $\left(\dfrac{1}{2}, \dfrac{1}{4}\right)$ और त्रिज्या $\dfrac{1}{12}$
उत्तर दिखाएं
उत्तर :
केंद्र $\left(h, k\right)$ और त्रिज्या $r$ वाले एक वृत्त का समीकरण निम्नलिखित होता है
$\left(x - h\right)^{2}+\left(y - k\right)^{2}=r^{2}$
दिया गया है कि केंद्र $\left(h, k\right)=\left(\dfrac{1}{2}, \dfrac{1}{4}\right)$ और त्रिज्या $\left(r\right)=\dfrac{1}{12}$
इसलिए, वृत्त का समीकरण है
$ \begin{aligned} & \left(x-\dfrac{1}{2}\right)^{2}+\left(y-\dfrac{1}{4}\right)^{2}=\left(\dfrac{1}{12}\right)^{2} \\ \\ & x^{2}-x+\dfrac{1}{4}+y^{2}-\dfrac{y}{2}+\dfrac{1}{16}=\dfrac{1}{144} \\ \\ & x^{2}-x+\dfrac{1}{4}+y^{2}-\dfrac{y}{2}+\dfrac{1}{16}-\dfrac{1}{144}=0 \\ \\ & 144 x^{2}-144 x+36+144 y^{2}-72 y+9-1=0 \\ \\ & 144 x^{2}-144 x+144 y^{2}-72 y+44=0 \\ \\
& 36 x^{2}-36 x+36 y^{2}-18 y+11=0 \\ \\ & 36 x^{2}+36 y^{2}-36 x-18 y+11=0 \end{aligned} $
4. केंद्र $\left(1,1\right)$ और त्रिज्या $\sqrt{2}$
उत्तर दिखाएं
उत्तर :
केंद्र $\left(h, k\right)$ और त्रिज्या $r$ वाले एक वृत्त का समीकरण $\left(x - h\right)^{2}+\left(y - k\right)^{2}=r^{2}$ द्वारा दिया गया है
दिया गया है केंद्र $\left(h, k\right)=\left(1,1\right)$ और त्रिज्या $\left(r\right)=\sqrt{2}$
इसलिए, वृत्त का समीकरण है
$ \begin{aligned} & \left(x-1\right)^{2}+\left(y-1\right)^{2}=\left(\sqrt{2}\right)^{2} \\ \\ & x^{2}-2 x+1+y^{2}-2 y+1=2 \\ \\ & x^{2}+y^{2}-2 x-2 y=0 \end{aligned} $
5. केंद्र $\left(-a,-b\right)$ और त्रिज्या $\sqrt{a^{2}-b^{2}}$
उत्तर दिखाएं
उत्तर :
केंद्र $\left(h, k\right)$ और त्रिज्या $r$ वाले एक वृत्त का समीकरण निम्नलिखित है
$\left(x - h\right)^{2}+\left(y - k\right)^{2}=r^{2}$
दिया गया है केंद्र $\left(h, k\right)=\left(-a, -b\right)$ और त्रिज्या $\left(r\right)=\sqrt{a^{2}-b^{2}}$
इसलिए, वृत्त का समीकरण है
$ \begin{aligned} & \left(x+a\right)^{2}+\left(y+b\right)^{2}=\left(\sqrt{a^{2}-b^{2}}\right)^{2} \\ \\ & x^{2}+2 a x+a^{2}+y^{2}+2 b y+b^{2}=a^{2}-b^{2} \\ \\ & x^{2}+y^{2}+2 a x+2 b y+2 b^{2}=0 \end{aligned} $
निम्नलिखित प्रश्नों 6 से 9 में से प्रत्येक में वृत्त के केंद्र और त्रिज्या ज्ञात कीजिए।
6. $\left(x+5\right)^{2}+\left(y-3\right)^{2}=36$
उत्तर दिखाएं
उत्तर :
दिए गए वृत्त का समीकरण $\left(x+5\right)^{2}+\left(y-3\right)^{2}=36$ है
$\left(x+5\right)^{2}+\left(y-3\right)^{2}=36$
$ \lbrace x-\left(-5\right) \rbrace ^{2}+\left(y-3\right)^{2}=6^{2}$,
जो $ \left(x-h\right)^{2}+\left(y-k\right)^{2}=r^{2} $ के रूप में है,
जहाँ $h=-5, k=3$, और $r=6$
इसलिए, दिए गए वृत्त का केंद्र $\left(-5,3\right)$ है, जबकि इसकी त्रिज्या $6$ है।
7. $x^{2}+y^{2}-4 x-8 y-45=0$
उत्तर दिखाएं
उत्तर :
दिए गए वृत्त का समीकरण $ x^{2}+y^{2} - 4 x-8 y - 45=0$ है
$x^{2}+y^{2} -4 x - 8 y - 45=0$
$\Rightarrow\left(x^{2} - 4 x\right)+\left(y^{2} - 8 y\right)=45$
$\Rightarrow \lbrace x^{2} - 2\left(x\right)\left(2\right)+2^{2} \rbrace + \lbrace y^{2} - 2\left(y\right)\left(4\right)+4^{2} \rbrace $ $- 4 -16=45$
$\Rightarrow\left(x - 2\right)^{2}+\left(y - 4\right)^{2}=65$
$\Rightarrow\left(x - 2\right)^{2}+\left(y - 4\right)^{2}=\left(\sqrt{65}\right)^{2}$,
जो $ \left(x - h\right)^{2}+\left(y - k\right)^{2}=r^{2} $ के रूप में है, जहाँ $h=2, k=4$, और $r=\sqrt{65}$
इसलिए, दिए गए वृत्त केंद्र $ \left(2,4\right) $ है, जबकि इसकी त्रिज्या $ \sqrt{65} $ है
8. $x^{2}+y^{2}-8 x+10 y-12=0$
उत्तर दिखाएं
उत्तर :
दिए गए वृत्त का समीकरण $x^{2}+y^{2} - 8 x+10 y - 12=0$ है
$x^{2}+y^{2} - 8 x+10 y - 12=0$
$\Rightarrow\left(x^{2} - 8 x\right)+\left(y^{2}+10 y\right)=12$
$\Rightarrow \lbrace x^{2} - 2\left(x\right)\left(4\right)+4^{2} \rbrace + \lbrace y^{2}+2\left(y\right)\left(5\right)+5^{2} \rbrace - 16 - 25=12$
$\Rightarrow\left(x - 4\right)^{2}+\left(y+5\right)^{2}=53$
$\Rightarrow\left(x-4\right)^{2}+\left[ \lbrace y-\left(-5\right) \rbrace \right]^{2}=\left(\sqrt{53}\right)^{2}$,
जो $ \left(x - h\right)^{2}+\left(y - k\right)^{2}=r^{2} $ के रूप में है, जहाँ $h=4, k=- 5,$ और $ \ \ r=\sqrt{53}$
इसलिए, दिए गए वृत्त केंद्र $ \left( 4, - 5 \right) $ है, जबकि इसकी त्रिज्या $ \sqrt{53} $ है
9. $2 x^{2}+2 y^{2}-x=0$
उत्तर दिखाएं
उत्तर :
दिए गए वृत्त का समीकरण $2 x^{2}+2 y^{2} - x=0$ है
$ \begin{aligned} & 2 x^{2}+2 y^{2}-x=0 \\ \\ & \Rightarrow\left(2 x^{2}-x\right)+2 y^{2}=0 \\ \\ & \Rightarrow 2\left[\left(x^{2}-\dfrac{x}{2}\right)+y^{2}\right]=0 \\ \\ & \Rightarrow \left\lbrace x^{2}-2 \cdot x\left(\dfrac{1}{4}\right)+\left(\dfrac{1}{4}\right)^{2} \right\rbrace +y^{2}-\left(\dfrac{1}{4}\right)^{2}=0 \\ \\ `
$$ \Rightarrow\left(x-\dfrac{1}{4}\right)^{2}+\left(y-0\right)^{2}=\left(\dfrac{1}{4}\right)^{2}, \\ \\ &\text{ जो } \left(x - h\right)^{2}+\left(y - k\right)^{2}=r^{2} \text{ के रूप में है, जहाँ } h=\dfrac{1}{4}, k=0, \text{ और } r=\dfrac{1}{4} \end{aligned} $$
इसलिए, दिए गए वृत्त केंद्र $\left(\dfrac{1}{4}, 0\right)$ है, जबकि इसकी त्रिज्या $\dfrac{1}{4}$ है
10. बिंदुओं $\left(4,1\right)$ और $\left(6,5\right)$ से गुजरते हुए और जिसका केंद्र रेखा $4 x+y=16$ पर स्थित हो वाले वृत्त का समीकरण ज्ञात कीजिए
उत्तर दिखाएं
उत्तर :
आवश्यक वृत्त का समीकरण मान लीजिए $\left(x - h\right)^{2}+\left(y - k\right)^{2}=r^{2}$
क्योंकि वृत्त बिंदुओं $\left(4,1\right)$ और $\left(6,5\right)$ से गुजरता है,
$\left(4 - h\right)^{2}+\left(1 - k\right)^{2}=r^{2}\qquad \ldots(1)$
$\left(6 - h\right)^{2}+\left(5 - k\right)^{2}=r^{2}\qquad \ldots(2)$
केंद्र $\left(h, k\right)$ रेखा $4 x+y=16$ पर स्थित है,
$4 h+k=16$
समीकरण $\left(1\right)$ और $\left(2\right)$ से, हम प्राप्त करते हैं
$\left(4 - h\right)^{2}+\left(1 - k\right)^{2}=\left(6 - h\right)^{2}+\left(5 -{2} k\right)^{2}$
$\Rightarrow 16 - 8 h+h^{2}+1-2 k+k^{2}=36-12 h+h^{2}+25-10 k+k^{2}$
$\Rightarrow 16 - 8 h+1 - 2 k=36 - 12 h+25 - 10 k$
$\Rightarrow 4 h+8 k=44\qquad \ldots(3)$
$\Rightarrow h+2 k=11\qquad \ldots(4)$
समीकरण $\left(3\right)$ और $\left(4\right)$ को हल करने पर, हमें $h=3$ और $k=4$ प्राप्त होते हैं
$ h $ और $ k $ के मानों को समीकरण $\left(1\right)$ में रखने पर, हम प्राप्त करते हैं
$\left(4 - 3\right)^{2}+\left(1 -4\right)^{2}=r^{2}$
$\Rightarrow\left(1\right)^{2}+\left(- 3\right)^{2}=r^{2}$
$\Rightarrow 1+9=r^{2}$
$\Rightarrow r^{2}=10$
$\Rightarrow r=\sqrt{10}$
इसलिए, आवश्यक वृत्त का समीकरण है
$\left(x - 3\right)^{2}+\left(y - 4\right)^{2}=\left(\sqrt{10}\right)^{2}$
$x^{2} - 6 x+9+y^{2} - 8 y+16=10$
$x^{2}+y^{2} -6 x-8 y+15=0$
11. बिंदुओं $\left(2,3\right)$ और $\left(-1,1\right)$ से गुजरते हुए और जिसका केंद्र रेखा $x-3 y-11=0$ पर स्थित हो वाले वृत्त का समीकरण ज्ञात कीजिए
उत्तर दिखाएँ
उत्तर :
आवश्यक वृत्त के समीकरण को $\left(x - h\right)^{2}+\left(y - k\right)^{2}=r^{2}$ मान लीजिए
क्योंकि वृत्त बिंदुओं $\left(2,3\right)$ और $\left( - 1,1 \right)$ से गुजरता है,
$\left(2 - h\right)^{2}+\left(3 - k\right)^{2}=r^{2} \qquad\ldots\left(1\right)$
$\left(- 1 - h\right)^{2}+\left(1 - k\right)^{2}=r^{2}\qquad \ldots(2)$
क्योंकि वृत्त के केंद्र $\left(h, k\right)$ रेखा $ x -3 y - 11=0 $ पर स्थित है,
$h - 3 k=11\qquad \ldots(3)$
समीकरण $\left(1\right)$ और $\left(2\right)$ से, हम प्राप्त करते हैं
$ \left(2-h\right)^2 + \left(3-k\right)^2 =\left(-1-h\right)^2 + \left(1-k\right)^2 $
$\Rightarrow 4 - 4 h+h^{2}+9 - 6 k+k^{2}=1+2 h+h^{2}+1 - 2 k+k^{2}$
$\Rightarrow 4 - 4 h+9 - 6 k=1+2 h+1 - 2 k$
$\Rightarrow 6 h+4 k=11\qquad \ldots(4)$
समीकरण $\left(3\right)$ और $\left(4\right)$ को हल करने पर, हमें $h=\dfrac{7}{2}$ और $k=\dfrac{-5}{2}$ प्राप्त होते हैं
$h$ और $k$ के मान को समीकरण $\left(1\right)$ में रखने पर, हम प्राप्त करते हैं
$\left(2-\dfrac{7}{2}\right)^{2}+\left(3+\dfrac{5}{2}\right)^{2}=r^{2}$
$\Rightarrow\left(\dfrac{4-7}{2}\right)^{2}+\left(\dfrac{6+5}{2}\right)^{2}=r^{2}$
$\Rightarrow\left(\dfrac{-3}{2}\right)^{2}+\left(\dfrac{11}{2}\right)^{2}=r^{2}$
$\Rightarrow \dfrac{9}{4}+\dfrac{121}{4}=r^{2}$
$\Rightarrow \dfrac{130}{4}=r^{2}$
इसलिए, आवश्यक वृत्त का समीकरण है
$ \begin{aligned} & \left(x-\dfrac{7}{2}\right)^{2}+\left(y+\dfrac{5}{2}\right)^{2}=\dfrac{130}{4} \\ \\ & \left(\dfrac{2 x-7}{2}\right)^{2}+\left(\dfrac{2 y+5}{2}\right)^{2}=\dfrac{130}{4} \\ \\ & 4 x^{2}-28 x+49+4 y^{2}+20 y+25=130 \\ \\ & 4 x^{2}+4 y^{2}-28 x+20 y-56=0 \\ \\ & 4\left(x^{2}+y^{2}-7 x+5 y-14\right)=0 \\ \\ & x^{2}+y^{2}-7 x+5 y-14=0 \end{aligned} $
12. वृत्त का समीकरण ज्ञात कीजिए जिसकी त्रिज्या 5 है और जो $x$-अक्ष पर स्थित केंद्र वाला है तथा बिंदु $\left(2,3\right)$ से गुजरता है
उत्तर दिखाएँ
उत्तर :
आवश्यक वृत्त के समीकरण को $\left(x - h\right)^{2}+\left(y - k\right)^{2}=r^{2}$ मान लीजिए
क्योंकि वृत्त की त्रिज्या 5 है और इसका केंद्र $x$-अक्ष पर स्थित है, $k=0$ और $r=5$
अब, वृत्त का समीकरण $\left(x - h\right)^{2}+y^{2}=25$ हो जाता है
दिया गया है कि वृत्त बिंदु $\left(2,3\right)$ से गुजरता है
$\therefore \ \left(2-h\right)^{2}+3^{2}=25$
$\Rightarrow\left(2-h\right)^{2}=25-9$
$\Rightarrow\left(2-h\right)^{2}=16$
$\Rightarrow 2-h= \pm \sqrt{16}= \pm 4$
यदि $2-h=4$, तो $h=-2$
यदि $2-h=-4$, तो $h=6$
जब $h=-2$ हो, तो वृत्त का समीकरण निम्नलिखित हो जाता है
$\left(x+2\right)^{2}+y^{2}=25$
$x^{2}+4 x+4+y^{2}=25$
$x^{2}+y^{2}+4 x - {21}=0$
जब $h=6$, तो वृत्त का समीकरण निम्नलिखित हो जाता है
$\left(x \text{ - 6 }\right)^{2}+y^{2}=25$
$ x^2 - 12x + 36 +y^2 = 25 $
$x^{2}+y^{2} - 12 x+11=0$
13. बिंदु $\left(0,0\right)$ से गुजरते हुए और निर्देशांक अक्षों पर $a$ और $b$ अपवार्तियाँ बनाने वाले वृत्त का समीकरण ज्ञात कीजिए।
उत्तर दिखाएं
Answer :
आवश्यक वृत्त का समीकरण मान लीजिए $\left(x - h\right)^{2}+\left(y - k\right)^{2}=r^{2}$
क्योंकि वृत्त $\left(0,0\right)$ से गुजरता है,
$\left(0 - h\right)^{2}+\left(0 - k\right)^{2}=r^{2}$
$\Rightarrow h^{2}+k^{2}=r^{2}$
अब वृत्त का समीकरण $\left(x - h\right)^{2}+\left(y - k\right)^{2}=h^{2}+k^{2}$ हो जाता है
दिया गया है कि वृत्त निर्देशांक अक्षों पर $a$ और $b$ अपवार्तियाँ बनाता है।
इसका अर्थ है कि वृत्त बिंदु $\left(a, 0\right)$ और $\left(0, b\right)$ से गुजरता है। अतः,
$\left(a - h\right)^{2}+\left(0 - k\right)^{2}=h^{2}+k^{2}\qquad \ldots(1)$
$\left(0 - h\right)^{2}+\left(b - k\right)^{2}=h^{2}+k^{2}\qquad \ldots(2)$
समीकरण $\left(1\right)$ से हम प्राप्त करते हैं
$a^{2} - 2 a h+h^{2}+k^{2}=h^{2}+k^{2}$
$\Rightarrow a^{2} - 2 a h=0$
$\Rightarrow a\left(a - 2 h\right)=0$
$\Rightarrow a=0$ या $\left(a - 2 h\right)=0$
हालांकि, $a \neq 0$
अतः, $\left(a - 2 h\right)=0 \Rightarrow h=2$
समीकरण $\left(2\right)$ से हम प्राप्त करते हैं
$h^{2}+b^{2} - 2 b k+k^{2}=h^{2}+k^{2}$
$\Rightarrow b^{2} - 2 b k=0$
$\Rightarrow b\left(b - 2 k\right)=0$
$\Rightarrow b=0$ या $\left(b - 2 k\right)=0$
हालांकि, $b \neq 0$
अतः, $\left( b - 2 k\right)=0 \Rightarrow k=\dfrac{b}{2}$
इसलिए, अभीष्ट वृत्त का समीकरण है
$ \begin{aligned} & \left(x-\dfrac{a}{2}\right)^{2}+\left(y-\dfrac{b}{2}\right)^{2}=\left(\dfrac{a}{2}\right)^{2}+\left(\dfrac{b}{2}\right)^{2} \\ \\ & \Rightarrow\left(\dfrac{2 x-a}{2}\right)^{2}+\left(\dfrac{2 y-b}{2}\right)^{2}=\dfrac{a^{2}+b^{2}}{4} \\ \\ & \Rightarrow 4 x^{2}-4 a x+a^{2}+4 y^{2}-4 b y+b^{2}=a^{2}+b^{2} \\ \\ & \Rightarrow 4 x^{2}+4 y^{2}-4 a x-4 b y=0 \\ \\ & \Rightarrow x^{2}+y^{2}-a x-b y=0 \end{aligned} $
14. केंद्र $\left(2,2\right)$ वाले एक वृत्त का समीकरण ज्ञात कीजिए जो बिंदु $\left(4,5\right)$ से गुजरता हो।
उत्तर दिखाएं
Answer :
वृत्त के केंद्र को $\left(h, k\right)=\left(2,2\right)$ दिया गया है
क्योंकि वृत्त बिंदु $\left(4,5\right)$ से गुजरता है, तो वृत्त की त्रिज्या $\left(r\right)$ बिंदुओं $\left(2,2\right)$ और $\left(4, 5\right)$ के बीच की दूरी है।
$ \therefore r=\sqrt{\left(2-4\right)^{2}+\left(2-5\right)^{2}}=\sqrt{\left(-2\right)^{2}+\left(-3\right)^{2}}=\sqrt{4+9}=\sqrt{13} $
इसलिए, वृत्त का समीकरण है
$ \begin{aligned} & \left(x-h\right)^{2}+\left(y-k\right)^{2}=r^{2} \\ \\ & \left(x-2\right)^{2}+\left(y-2\right)^{2}=\left(\sqrt{13}\right)^{2} \\ \\ & x^{2}-4 x+4+y^{2}-4 y+4=13 \\ \\ & x^{2}+y^{2}-4 x-4 y-5=0 \end{aligned} $
15. बिंदु $\left(-2.5,3.5\right)$ वृत्त $x^{2}+y^{2}=25$ के अंदर, बाहर या वृत्त पर स्थित है?
उत्तर दिखाएं
Answer :
दिए गए वृत्त का समीकरण $x^{2}+y^{2}=25$ है
$x^{2}+y^{2}=25$
$\Rightarrow\left(x - 0\right)^{2}+\left(y - 0\right)^{2}=5^{2}$, जो $\left(x - h\right)^{2}+\left(y - k\right)^{2}=r^{2}$ के रूप में है,
जहाँ $h=0, k=0$, और $r=5$
$\therefore \ $ केंद्र $=\left(0,0\right)$ और त्रिज्या $=5$
बिंदु $\left(-2.5, 3.5\right)$ और केंद्र $\left(0,0\right)$ के बीच की दूरी
है
$ \begin{aligned} & =\sqrt{\left(-2.5-0\right)^{2}+\left(3.5-0\right)^{2}} \\ \\ & =\sqrt{6.25+12.25} \\ \\ & =\sqrt{18.5} \\ \\ & =4.3\left(\text{ approx. }\right)<5 \end{aligned} $
क्योंकि बिंदु $\left(-2.5,3.5\right)$ और वृत्त के केंद्र $\left(0,0\right)$ के बीच की दूरी वृत्त की त्रिज्या से कम है, बिंदु $\left(-2.5, 3.5\right)$ वृत्त के अंदर स्थित है।
10.4 पराबोला
परिभाषा 2 एक तल में एक निश्चित रेखा और एक निश्चित बिंदु (रेखा पर नहीं) से समान दूरी पर स्थित सभी बिंदुओं के समूह को पराबोला कहते हैं।
इस निश्चित रेखा को पराबोला की अक्ष कहते हैं और निश्चित बिंदु $F$ को फोकस कहते हैं (चित्र 10.13)। (‘Para’ का अर्थ है ‘लिए’ और ‘bola’ का अर्थ है ‘छोड़ना’, अर्थात जब आप एक गेंद एक ऊपर फेंकते हैं तो उस आकृति का वर्णन करता है)।

चित्र 10.13
नोट - यदि निश्चित बिंदु निश्चित रेखा पर स्थित हो, तो तल में निश्चित बिंदु और निश्चित रेखा से समान दूरी पर बिंदुओं के समूह को निश्चित बिंदु से गुजरती और निश्चित रेखा के लम्ब एक सीधी रेखा कहते हैं। हम इस सीधी रेखा को परवलय के अपरिवर्ती मामला कहते हैं।
फोकस से गुजरती और नियतांक रेखा के लम्ब एक रेखा को परवलय के अक्ष कहते हैं। परवलय और अक्ष के प्रतिच्छेद बिंदु को परवलय के शीर्ष कहते हैं (चित्र 10.14)।

चित्र 10.14
10.4.1 परवलय के मानक समीकरण
एक परवलय के समीकरण को सरलतम रूप में जब उसका शीर्ष मूल बिंदु पर हो और सममिति अक्ष $x$-अक्ष या $y$-अक्ष के अनुदिश हो, तब लिखा जाता है। परवलय के चार संभावित ऐसे आकृतियाँ नीचे चित्र 10.15 (a) से (d) में दिखाई गई हैं।

(a)

(b)

(c)

(d)
हम उपरोक्त आकृति 10.15 (a) में दिखाए गए परवलय के समीकरण का निर्वचन करेंगे जिसका फोकस $(a, 0)$, $a>0$ है; और नियतक $x=-a$ है जैसा कि नीचे दिखाया गया है:
मान लीजिए $F$ फोकस है और $l$ नियतक है। मान लीजिए FM नियतक के लंबवत है और FM को बिंदु O पर समद्विभाजित करता है। MO को X तक बढ़ाएं। परवलय के परिभाषा के अनुसार, मध्य बिंदु $O$ परवलय पर स्थित है और इसे परवलय का शीर्ष कहते हैं। $O$ को मूल बिंदु, $OX$ को $x$-अक्ष और $OY$ को $OX$ के लंबवत अक्ष के रूप में ले लीजिए। मान लीजिए नियतक से फोकस तक की दूरी $2a$ है। तब, फोकस के निर्देशांक $(a, 0)$ हैं, और नियतक का समीकरण $x + a = 0$ है जैसा कि आकृति 10.16 में दिखाया गया है।

चित्र $\mathbf{1 0 . 1 6}$
मान लीजिए $P(x, y)$ एक ऐसा बिंदु है जो परवलय पर कोई भी बिंदु है जैसे कि
$ PF=PB, \quad \quad\quad\quad\quad\quad\quad\quad\quad\ldots(1) $
जहाँ $PB$ रेखा $l$ पर लम्ब है। $B$ के निर्देशांक $(-a, y)$ हैं। दूरी सूत्र के अनुसार, हम निम्नलिखित प्राप्त करते हैं
$ PF=\sqrt{(x-a)^{2}+y^{2}} ~\text{ और } ~PB=\sqrt{(x+a)^{2}}
$
क्योंकि $PF=PB$, हम निम्नलिखित प्राप्त करते हैं
$ \sqrt{(x-a)^{2}+y^{2}}=\sqrt{(x+a)^{2}} $
अर्थात $ \quad\quad\quad(x-a)^{2}+y^{2}=(x+a)^{2}$
या $\quad\quad\quad x^{2}-2 a x+a^{2}+y^{2}=x^{2}+2 a x+a^{2}$
या $\quad\quad\quad y^{3}=4 a x(a>0)$.
अतः, परवलय पर कोई भी बिंदु समीकरण
$ y^{2}=4 a x \quad \quad\quad\quad\quad\quad\quad\quad\quad\ldots(2) $
को संतुष्ट करता है।
विलोमतः, मान लीजिए $P(x, y)$ समीकरण (2) को संतुष्ट करता है
$ \begin{aligned} PF & =\sqrt{(x-a)^{2}+y^{2}} \quad=\sqrt{(x-a)^{2}+4 a x} \\ & =\sqrt{(x+a)^{2}}=PB \quad \quad\quad\quad\quad\quad\quad\quad\quad\ldots(3)
\end{aligned} $
और इस प्रकार $P(x, y)$ पराबोला पर स्थित है।
इसलिए, समीकरण (2) और (3) से हम यह सिद्ध कर सकते हैं कि मूल बिंदु पर शीर्ष, फोकस $(a, 0)$ पर और नियता $x = -a$ पर पराबोला के समीकरण $y^{2} = 4 a x$ है।
चर्चा समीकरण (2) में, क्योंकि $a > 0$, $x$ केवल धनात्मक मान या शून्य ले सकता है लेकिन नकारात्मक मान नहीं ले सकता और वक्र पहले और चौथे चतुर्थांश में अनंत तक फैलता है। पराबोला का अक्ष धनात्मक $x$-अक्ष है।
उसी तरह, हम इन चारों दिशाओं में पराबोला के समीकरण निकाल सकते हैं:
चित्र 11.15 (b) के रूप में $y^{2}=-4 a x$,
चित्र 11.15 (c) के रूप में $x^{2}=4 a y$,
चित्र $11.15(d)$ के रूप में $x^{2}=-4 a y$,
इन चार समीकरणों को परवलय के मानक समीकरण के रूप में जाना जाता है।
नोट - परवलय के मानक समीकरण एक निर्देशांक अक्ष पर फोकस रखते हैं; मूल बिंदु पर शीर्ष रखते हैं और इसलिए नियतांक एक अन्य निर्देशांक अक्ष के समानांतर होता है। हालांकि, फोकस किसी भी बिंदु पर और किसी भी रेखा के रूप में नियतांक वाले परवलय के समीकरणों के अध्ययन के बारे में यहां बाहर के विषय के बारे में है।
मानक परवलय समीकरणों से, चित्र 10.15, हम निम्नलिखित अवलोकन कर सकते हैं:
1. पराबोला अपने अक्ष के संदर्भ में सममित होती है। यदि समीकरण में $y^{2}$ शब्द होता है, तो सममिति अक्ष $x$-अक्ष के अनुदिश होता है और यदि समीकरण में $x^{2}$ शब्द होता है, तो सममिति अक्ष $y$-अक्ष के अनुदिश होता है।
2. जब सममिति अक्ष $x$-अक्ष के अनुदिश होता है, तो पराबोला खुलती है
(a) दाहिने ओर यदि $x$ के गुणांक धनात्मक हो,
(b) बाएँ ओर यदि $x$ के गुणांक ऋणात्मक हो।
3. जब सममिति अक्ष $y$-अक्ष के अनुदिश होता है, तो पराबोला खुलती है
(c) ऊपर जाएगी यदि $y$ के गुणांक धनात्मक हो।
(d) नीचे जाएगी यदि $y$ के गुणांक ऋणात्मक हो।
10.4.2 लैटस रेक्टम
परिभाषा 3 एक परवलय के लैटस रेक्टम एक रेखाखंड होता है जो परवलय के अक्ष के लंबवत होता है, फोकस से गुजरता है और जिसके सिरे परवलय पर स्थित होते हैं (चित्र 10.17)।

चित्र 10.17
परवलय $ y^{2}= 4 a x $ के लatus rectum की लंबाई ज्ञात करें (चित्र 10.18)।

चित्र 10.18
परवलय के परिभाषा के अनुसार, $AF=AC$।
लेकिन $ ~\mathrm{AC}=\mathrm{FM}=2 a $
अतः $ ~\mathrm{AF}=2 a $
और क्योंकि परवलय $x$-अक्ष के सापेक्ष सममित है, $AF=FB$ और इसलिए
$AB=$ लatus rectum की लंबाई $=4 a$।
उदाहरण 5 परवलय $y^{2}=8 x$ के फोकस के निर्देशांक, अक्ष, सीधर रेखा के समीकरण और लैटस रेक्टम के समीकरण ज्ञात कीजिए।
हल दी गई समीकरण में $y^{2}$ है, इसलिए सममिति अक्ष $x$-अक्ष के अनुदिश है।
$x$ के गुणांक धनात्मक है, इसलिए परवलय दाहिने ओर खुलता है। दी गई समीकरण $y^{2}=4 a x$ के साथ तुलना करने पर हम जानते हैं कि $a=2$।
इसलिए, परवलय के फोकस के निर्देशांक $(2,0)$ है और परवलय के सीधर रेखा के समीकरण $x=-2$ है (चित्र 10.19)।

चित्र 10.19
लेटस रेक्टम की लंबाई $4 a=4 \times 2=8$ है।
उदाहरण 6 फोकस $(2,0)$ और नियता $x=-2$ वाले परवलय का समीकरण ज्ञात कीजिए।
हल चूंकि फोकस $(2,0)$ $x$-अक्ष पर स्थित है, इसलिए $x$-अक्ष खुद परवलय का अक्ष है। अतः परवलय का समीकरण $y^{2}=4 a x$ या $y^{2}=-4 a x$ के रूप में हो सकता है। चूंकि नियता $x=-2$ और फोकस $(2,0)$ है, इसलिए परवलय का रूप $y^{2}=4 a x$ होगा जहां $a=2$ है। अतः अभीष्ट समीकरण है
$ y^{2}=4(2) x=8 x $
उदाहरण 7 शीर्ष $(0,0)$ और फोकस $(0,2)$ पर वाले परवलय का समीकरण ज्ञात कीजिए।
हल चूंकि शीर्ष $(0,0)$ पर है और फोकस $(0,2)$ जो $y$-अक्ष पर स्थित है, इसलिए $y$-अक्ष परवलय का अक्ष है। अतः परवलय का समीकरण $x^{2}=4 a y$ के रूप में होगा। इसलिए हमें प्राप्त होता है
$ x^{2}=4(2) y \text{, अर्थात } x^{3}=8 y \text{। } $
उदाहरण 8 $y$-अक्ष के सममित परवलय का समीकरण ज्ञात कीजिए जो बिंदु $(2,-3)$ से गुजरता हो।
हल चूंकि परवलय $y$-अक्ष के सापेक्ष सममित है और इसका शीर्ष मूल बिंदु पर है, इसका समीकरण $x^{2}=4 a y$ या $x^{2}=-4 a y$ के रूप में होता है, जहां चिह्न उस तथ्य पर निर्भर करता है कि परवलय ऊपर या नीचे खुलता है। लेकिन परवलय $(2,-3)$ से गुजरता है जो चतुर्थ चतुर्थांश में स्थित है, इसलिए यह नीचे खुलता है। अतः इसका समीकरण $x^{2}=-4 a y$ के रूप में होता है।
चूंकि परवलय $(2,-3)$ से गुजरता है, हमें निम्न प्राप्त होता है:
$ 2^{2}=-4 a(-3) \text{, अर्थात } a=\dfrac{1}{3} $
इसलिए, परवलय का समीकरण
$ x^{2}=-4(\dfrac{1}{3}) y \text{, i.e., } 3 x^{2}=-4 y $
अभ्यास 10.2
निम्नलिखित प्रत्येक अभ्यास (1 से 6) में, परवलय के फोकस के निर्देशांक, अक्ष, सीधर्त्र रेखा की समीकरण और लैटस रेखा की लम्बाई ज्ञात कीजिए।
1. $y^{2}=12 x$
उत्तर दिखाएँ
उत्तर :

दी गई समीकरण $y^{2}=12 x$ है।
यहाँ, $x$ के गुणांक धनात्मक है।
अतः, परवलय दाहिनी ओर खुलती है।
इस समीकरण को $y^{2}=4 a x$ के साथ तुलना करने पर,
हम प्राप्त करते हैं $4 a=12 $ $\Rightarrow a=3$
$\therefore \ \ $ फोकस के निर्देशांक $=\left(a, 0\right)=\left(3,0\right)$
क्योंकि दी गई समीकरण में $y^{2}$ है, अतः परवलय का अक्ष $x$-अक्ष है।
सीधर्त्र रेखा की समीकरण, $x=-a \ $ अर्थात $x=-3$ अर्थात $x+3=0$
लैटस रेखा की लम्बाई $=4 a=4 \times 3=12$
2. $x^{2}=6 y$
उत्तर दिखाएँ
उत्तर :

दी गई समीकरण $x^{2}=6 y$ है।
यहाँ, $y$ के गुणांक धनात्मक है।
अतः, परवलय ऊपर खुलती है।
इस समीकरण को $x^{2}=4 a y$ के साथ तुलना करने पर,
हम प्राप्त करते हैं $4 a=6 $ $\Rightarrow a=\dfrac{3}{2}$
$\therefore \ \ $ फोकस के निर्देशांक $=\left(0, a\right)=\left(0, \dfrac{3}{2}\right)$
क्योंकि दी गई समीकरण में $x^{2}$ है, अतः परवलय का अक्ष $y$-अक्ष है।
सीधर्त्र रेखा की समीकरण,
$ y=-a \text{ अर्थात } y=-\dfrac{3}{2} $
लैटस रेखा की लम्बाई $=4 a=6$
3. $y^{2}=-8 x$
उत्तर दिखाएँ
उत्तर :

दी गई समीकरण $y^{2}=-8 x$ है।
यहाँ, $x$ के गुणांक ऋणात्मक है।
अतः, परवलय बाएँ ओर खुलती है।
दिए गए समीकरण की तुलना $y^{2}=-4 a x$ से करते हुए,
हम प्राप्त करते हैं $-4 a=-8 \Rightarrow a=2$
$\therefore \ \ $ फोकस के निर्देशांक $=\left(-a, 0\right)=\left(-2,0\right)$
क्योंकि दिए गए समीकरण में $y^{2}$ है, परबोला का अक्ष $x$-अक्ष है।
सीधेकर्त्र रेखा का समीकरण, $x=$ a $\quad$ अर्थात, $x=2$
लैटस रेक्टम की लंबाई $=4 a=8$
4. $x^{2}=-16 y$
उत्तर दिखाएं
उत्तर :

दिए गए समीकरण $x^{2}=-16 y$ है
यहाँ, $y$ के गुणांक नकारात्मक है।
अतः, परबोला नीचे की ओर खुलती है।
दिए गए समीकरण की तुलना $x^{2}=-4 a y$ से करते हुए,
हम प्राप्त करते हैं $-4 a=-16 \Rightarrow a=4$
$\therefore \ \ $ फोकस के निर्देशांक $=\left(0,-a\right)=\left(0,-4\right)$
क्योंकि दिए गए समीकरण में $x^{2}$ है, परबोला का अक्ष $y$-अक्ष है।
सीधेकर्त्र रेखा का समीकरण, $y=a\quad$ अर्थात, $y=4$
लैटस रेक्टम की लंबाई $=4 a=16$
5. $y^{2}=10 x$
उत्तर दिखाएं
उत्तर :

दिए गए समीकरण $y^{2}=10 x$ है
यहाँ, $x$ के गुणांक धनात्मक है।
अतः, परबोला दाईं ओर खुलती है।
दिए गए समीकरण की तुलना $y^{2}=4 a x$ से करते हुए,
हम प्राप्त करते हैं
$4 a=10 \Rightarrow a=\dfrac{5}{2}$
$\therefore \ \ $ फोकस के निर्देशांक $=\left(a, 0\right)$ $ =\left(\dfrac{5}{2}, 0\right) $
क्योंकि दिए गए समीकरण में $y^{2}$ है, परबोला का अक्ष $x$-अक्ष है।
सीधेकर्त्र रेखा का समीकरण,
$ x=-a \quad\text{ अर्थात, } x=-\dfrac{5}{2} $
लैटस रेक्टम की लंबाई $=4 a=10$
6. $x^{2}=-9 y$
उत्तर दिखाएं
उत्तर :

दिए गए समीकरण $x^{2}=-9 y$ है
यहाँ, $y$ के गुणांक नकारात्मक है।
इसलिए, परवलय नीचे की ओर खुलता है।
इस समीकरण को $x^{2}=4a y $ से तुलना करने पर
हम प्राप्त करते हैं $-4 a=-9 \Rightarrow b=\dfrac{9}{4}$
$\therefore \ \ $ फोकस के निर्देशांक $=\left(0,-a\right)=\left(0,-\dfrac{9}{4}\right)$
क्योंकि दिए गए समीकरण में $x^{2}$ है, इसलिए परवलय का अक्ष $y$-अक्ष है।
सीधी रेखा का समीकरण,
$ y=a \quad\text{ अर्थात } y=\dfrac{9}{4} $
लैटस रेक्टम की लम्बाई $=4 a=9$
प्रत्येक अभ्यास 7 से 12 तक में, दिए गए शर्तों को संतुष्ट करने वाले परवलय का समीकरण ज्ञात कीजिए:
7. फोकस $\left(6,0\right)$; सीधी रेखा $x=-6$
उत्तर दिखाएं
उत्तर :
फोकस $\left(6,0\right)$; सीधी रेखा, $x=-6$
क्योंकि फोकस $x$-अक्ष पर स्थित है, इसलिए $x$-अक्ष परवलय का अक्ष है।
इसलिए, परवलय का समीकरण $y^{2}=4 a x$ या $y^{2}=-4 a x$ के रूप में हो सकता है।
यह भी देखा जा सकता है कि सीधी रेखा, $x=-6$ $y$-अक्ष के बाईं ओर है, जबकि फोकस $\left(6,0\right)$ $y$-अक्ष के दाईं ओर है।
इसलिए, परवलय का रूप $y^{2}=4 a x$ है।
यहाँ, $a=6$
इसलिए, परवलय का समीकरण $y^{2}=24 x$ है।
8. शीर्ष $\left(0,0\right)$; फोकस $\left(3,0\right)$
उत्तर दिखाएं
उत्तर :
शीर्ष $\left(0,0\right)$; फोकस $\left(3,0\right)$
क्योंकि परवलय का शीर्ष $\left(0,0\right)$ है और फोकस धनात्मक $x$-अक्ष पर स्थित है, इसलिए $x$-अक्ष परवलय का अक्ष है, जबकि परवलय का समीकरण $y^{2}=4 a x$ के रूप में होता है।
क्योंकि फोकस $\left(3,0\right)$ है, तो $a=3$
इसलिए, परवलय का समीकरण $y^{2}=4x \times 3$ अर्थात $y^{2}=12 x$ है।
9. फोकस $\left(0,-3\right)$; सीधी रेखा $y=3$
उत्तर दिखाएं
उत्तर :
फोकस $=\left(0,-3\right) ;$ सीधी रेखा $y=3$
क्योंकि फोकस $y$-अक्ष पर स्थित है, इसलिए $y$-अक्ष परवलय का अक्ष है।
इसलिए, परवलय का समीकरण $x^{2}=4ay$ या $x^{2}=-4 a y$ के रूप में हो सकता है।
यह भी देखा जा सकता है कि सीधी रेखा, $y=3$ $x$-अक्ष के ऊपर है, जबकि फोकस
$\left(0,-3\right)$, $x$-अक्ष के नीचे है।
इसलिए, परवलय के रूप में $x^{2}=-4 a y$ है
यहाँ, $a=3$
इसलिए, परवलय का समीकरण $x^{2}=-12 y$ है
10. शीर्ष $\left(0,0\right)$; फोकस $\left(-2,0\right)$
उत्तर दिखाएं
उत्तर :
शीर्ष $\left(0,0\right)$ फोकस $\left(-2,0\right)$
क्योंकि परवलय का शीर्ष $\left(0,0\right)$ है और फोकस नकारात्मक $x$-अक्ष पर स्थित है, $x$-अक्ष परवलय का अक्ष है, जबकि परवलय का समीकरण $y^{2}=-4 a x$ के रूप में है
क्योंकि फोकस $\left(-2,0\right)$ है, $a=2$
इसलिए, परवलय का समीकरण $y^{2}=-4\left(2\right) x\quad$, अर्थात $y^{2}=-8 x$ है
11. शीर्ष $\left(0,0\right)$, $\left(2,3\right)$ से गुजरता है और अक्ष $x$-अक्ष के अनुदिश है।
उत्तर दिखाएं
उत्तर :
क्योंकि शीर्ष $\left(0,0\right)$ है और परवलय का अक्ष $x$-अक्ष है, परवलय का समीकरण $ ~ y^{2}=4 a x ~ $ या $ ~ y^{2}=- 4 a x ~ $ के रूप में हो सकता है
परवलय $\left(2,3\right)$ से गुजरता है, जो प्रथम चतुर्थांश में है।
इसलिए, परवलय का समीकरण $y^{2}=4 a x$ के रूप में है, जबकि बिंदु $\left(2,3\right)$ समीकरण $y^{2}=4 a x$ को संतुष्ट करता है $y^{2}=4 a x$
$\therefore \ \ 3^{2}=4 a\left(2\right) \Rightarrow a=\dfrac{9}{8}$
इसलिए, परवलय का समीकरण है
$ \begin{aligned} & y^{2}=4\left(\dfrac{9}{8}\right) x \\ \\ & y^{2}=\dfrac{9}{2} x \\ \\ & 2 y^{2}=9 x \end{aligned} $
12. शीर्ष $\left(0,0\right)$, $\left(5,2\right)$ से गुजरता है और $y$-अक्ष के संबंध में सममित है।
उत्तर दिखाएं
उत्तर :
क्योंकि शीर्ष $\left(0,0\right)$ है और परवलय $y$-अक्ष के संबंध में सममित है, परवलय का समीकरण $ ~ x^{2}=4 ay$ या $ ~ x^{2}=- 4ay$ के रूप में हो सकता है
परवलय $\left(5,2\right)$ से गुजरता है, जो प्रथम चतुर्थांश में है।
इसलिए, परवलय का समीकरण $x^{2}=4 a y$ के रूप में है, जबकि बिंदु
$\left(5,2\right)$ समीकरण $x^{2}=4 a y$ को संतुष्ट करता है
$\therefore \ \ \left(5\right)^{2}=4 \times a \times 2 $
$\quad\Rightarrow 25=8 a \Rightarrow a=\dfrac{25}{8}$
इसलिए, पराबोला का समीकरण है $x^{2}=4\left(\dfrac{25}{8}\right) y$
$2 x^{2}=25 y$
10.5 अतिपरवलय
परिभाषा 4 एक तल में ऐसे सभी बिंदुओं के समुच्चय जिनके दो निश्चित बिंदुओं से कुल दूरी एक निश्चित संख्या होती है, एक अतिपरवलय कहलाता है।
इन दो निश्चित बिंदुओं को अतिपरवलय के फोकस (एक शब्द के बहुवचन) कहते हैं (चित्र 10.20)।

चित्र 10.20
नोट - एक बिंदु की दो स्थिर बिंदुओं से दूरी के योग के बराबर अचर राशि हमेशा दो स्थिर बिंदुओं के बीच की दूरी से बड़ी होती है।
फोकस के बीच रेखाखंड के मध्य बिंदु को वृत्ताकार वक्र का केंद्र कहते हैं। वृत्ताकार वक्र के फोकस से गुजरने वाले रेखाखंड को मुख्य अक्ष कहते हैं और मुख्य अक्ष के केंद्र से गुजरते हुए एवं मुख्य अक्ष के लंब रेखाखंड को न्यून अक्ष कहते हैं। मुख्य अक्ष के सिरे वृत्ताकार वक्र के शीर्ष कहलाते हैं (चित्र 10.21)।

चित्र 10.21
हम मुख्य अक्ष की लंबाई को $2 a$ से दर्शाते हैं, उपअक्ष की लंबाई को $2 b$ से और फोकस के बीच की दूरी को $2 c$ से। इस प्रकार, अर्ध मुख्य अक्ष की लंबाई $a$ होती है और अर्ध उपअक्ष की लंबाई $b$ होती है (चित्र 10.22)।

चित्र 10.22
10.5.1 अर्ध लम्ब अक्ष, अर्ध छोटी अक्ष और वृत्तीय बिंदु के केंद्र से दूरी के बीच संबंध (चित्र 10.23)

चित्र 10.23
कम अक्ष के एक सिरे पर एक बिंदु $P$ ले लो।
बिंदु $P$ से दो फोकस तक की दूरियों का योग
$F_1P + F_2P = F_1O + OP + F_2P$
(क्योंकि, $F_1P = F_1O + OP$)
$= c + a +a - c = 2a$
मान लीजिए कि बिंदु Q छोटी अक्ष के एक सिरे पर स्थित है।
बिंदु Q से फोकस तक की दूरियों का योग है
$F_1 P+F_2 Q=\sqrt{b^{2}+c^{2}}+\sqrt{b^{2}+3^{2}}=2 \sqrt{b^{2}+c^{2}}$
क्योंकि दोनों $P$ और $Q$ एलिप्स पर स्थित हैं।
एलिप्स के परिभाषा के अनुसार, हम लिख सकते हैं
$ \begin{aligned} 2 \sqrt{b^{2}+c^{2}} & =2 a, ~\text{ अर्थात } \quad a=\sqrt{b^{2}+c^{2}} \\ \text{या } \quad \quad \quad a^{2} & =b^{2}+c^{2}, \text{ अर्थात } c=\sqrt{a^{2}-b^{2}} \end{aligned} $
10.5.2 अपसारिता (Eccentricity)
परिभाषा 5 एक वृत्ताकार वक्र के असमानता केंद्र के एक फोकस और एक शीर्ष के बीच दूरी के अनुपात को इसकी असमानता कहते हैं (असमानता को $e$ से नोट किया जाता है) अर्थात, $e=\dfrac{c}{a}$।
फिर चूंकि फोकस केंद्र से $c$ की दूरी पर होता है, असमानता के संदर्भ में फोकस केंद्र से $ae$ की दूरी पर होता है।
10.5.3 एक वृत्ताकार वक्र के मानक समीकरण
एक वृत्ताकार वक्र का समीकरण उसके केंद्र को मूल बिंदु पर और फोकस $x$-अक्ष या $y$-अक्ष पर होने पर सबसे सरल होता है। ऐसे दो संभावित आकृतियाँ चित्र 10.24 में दिखाई गई हैं।
हम उपरोक्त आकृति 10.24 (a) के लिए वृत्तीय अपवाह के समीकरण का निर्वचन करेंगे जिसके दोनों फोकस $x$-अक्ष पर हैं।

मान लीजिए $F_1$ और $F_2$ फोकस हैं और $O$ रेखाखंड $F_1 F_2$ का मध्य बिंदु है। मान लीजिए $O$ मूल बिंदु है और $O$ से $F_2$ के माध्यम से जाने वाली रेखा धनात्मक $x$-अक्ष है और $F_1$ के माध्यम से जाने वाली रेखा ऋणात्मक $x$-अक्ष है। मान लीजिए $O$ से $x$-अक्ष के लंब रेखा धनात्मक $y$-अक्ष है। मान लीजिए $F_1$ के निर्देशांक $(-c, 0)$ हैं और $F_2$ के निर्देशांक $(c, 0)$ हैं (आकृति 10.25)।

चित्र 10.25
मान लीजिए $P(x, y)$ एक ऐसा बिंदु है जो वृत्त पर स्थित है जैसे कि $P$ के दो फोकसों से दूरी का योग $2 a$ हो, जैसा दिया गया है
$ PF_1+PF_2=2 a . \quad \quad \quad \quad \quad \quad \quad \ldots (1) $
दूरी सूत्र का उपयोग करते हुए, हम लिख सकते हैं
$ \begin{aligned} & \qquad \sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2 a \\
& \text{ अर्थात, } \sqrt{(x+c)^{2}+y^{2}}=2 a-\sqrt{(x-c)^{2}+y^{2}} \end{aligned} $
दोनों ओर वर्ग करने पर, हम प्राप्त करते हैं
$ (x+c)^{2}+y^{2}=4 a^{2}-4 a \sqrt{(x-c)^{2}+y^{2}}+(x-c)^{2}+y^{2} $
जिसके सरलीकरण से प्राप्त होता है
$ \sqrt{(x-c)^{2}+y^{2}}=a-\dfrac{c}{a} x $
फिर से वर्ग करके और सरल करके, हम प्राप्त करते हैं
$ \begin{aligned} \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{a^{2}-c^{2}}=1 & \\ \text{ अर्थात, } \quad \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1 & (\text{ क्योंकि } c^{2}=a^{2}-b^{2}) \end{aligned} $
अतः एल्लिप्स पर कोई भी बिंदु इस समीकरण को संतुष्ट करता है
$ \begin{aligned} \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1 \quad \quad \qquad \quad \quad \ldots(2) \end{aligned} $
विपरीत रूप से, मान लीजिए $P(x, y)$ समीकरण (2) को संतुष्ट करता है जहाँ $0 < c < a$. तब
$ y^{2}=b^{2}(1-\dfrac{x^{2}}{a^{2}}) $
इसलिए, $PF_1=\sqrt{(x+c)^{2}+y^{2}}$
$ \begin{aligned} & =\sqrt{(x+c)^{2}+b^{2}\left(\dfrac{a^{2}-x^{2}}{a^{2}}\right)} \\ & =\sqrt{(x+c)^{2}+(a^{2}-c^{2})\left(\dfrac{a^{2}-x^{2}}{a^{2}}\right)}(\text{ क्योंकि } b^{3}=a^{2}-c^{2}) \\ & =\sqrt{\left(a+\dfrac{c x}{a}\right)^{2}}=a+\dfrac{c}{a} x
\end{aligned} $
इसी तरह $\quad PF_2=a-\dfrac{c}{a} x$
इसलिए $\quad PF_1+PF_2=a+\dfrac{c}{a} x+a-\dfrac, x=2 a \quad \quad \quad \quad \quad \ldots(3)$
इसलिए, कोई भी बिंदु जो $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ को संतुष्ट करता है, ज्यामितीय स्थिति को संतुष्ट करता है और इसलिए $P(x, y)$ एलिप्स पर स्थित होता है।
इसलिए (2) और (3) से, हम निरूपण करते हैं कि केंद्र मूल बिंदु और मुख्य अक्ष $x$-अक्ष के अनुदिश एलिप्स का समीकरण है
$ \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1 $
चर्चा ऊपर प्राप्त एलिप्स के समीकरण से, यह निर्धारित होता है कि एलिप्स पर कोई भी बिंदु $P(x, y)$ इस प्रकार होता है कि
$ \dfrac{x^{2}}{a^{2}}=1-\dfrac{y^{2}}{b^{2}} \leq 1 \text{, i.e., } x^{2} \leq a^{2} \text{, so }-a \leq x \leq a \text{. } $
इसलिए, वृत्ताार वक्र $x=-a$ और $x=a$ के बीच स्थित होता है और इन रेखाओं को स्पर्श करता है।
उसी तरह, वृत्ताकार वक्र $y=-b$ और $y=b$ के बीच स्थित होता है और इन रेखाओं को स्पर्श करता है।
उसी तरह, आकृति 10.24 (b) में वृत्ताकार वक्र के समीकरण को $\dfrac{x^{2}}{b^{2}}+\dfrac{y^{2}}{a^{2}}=1$ के रूप में निर्मित किया जा सकता है।
इन दो समीकरणों को वृत्ताकार वक्रों के मानक समीकरण के रूप में जाना जाता है।
नोट - वृत्त के मानक समीकरणों में केंद्र मूल बिंदु पर होता है और मुख्य एवं लघु अक्ष निर्देशांक अक्ष होते हैं। हालांकि, इस अनुच्छेद में अन्य केंद्र पर वृत्त के अध्ययन और केंद्र से गुजरने वाली किसी रेखा को मुख्य अक्ष तथा केंद्र से गुजरने वाली और मुख्य अक्ष के लंब रेखा को लघु अक्ष के रूप में लेने वाले वृत्त के अध्ययन के बारे में बात नहीं की जाएगी।
मानक वृत्त के समीकरणों (चित्र 10.24) से हम निम्नलिखित अवलोकन कर सकते हैं:
1. वृत्त दोनों निर्देशांक अक्षों के सापेक्ष सममित होता है क्योंकि यदि $(x, y)$ एक वृत्त पर बिंदु है, तो $(-x, y),(x,-y)$ और $(-x,-y)$ भी वृत्त पर बिंदु होते हैं।
2. फोकस हमेशा मुख्य अक्ष पर स्थित होते हैं। मुख्य अक्ष को अक्ष के सममिति अक्ष पर अपवार्ति निर्धारित करके ज्ञात किया जा सकता है। अर्थात, यदि $x^{2}$ के गुणांक के बड़े हर के लिए मुख्य अक्ष $x$-अक्ष के अनुदिश होता है और यदि $y^{2}$ के गुणांक के बड़े हर के लिए मुख अक्ष $y$-अक्ष के अनुदिश होता है।
10.5.4 लैटस रेक्टम
परिभाषा 6 एक वृत्ताकार वक्र के लैटस रेक्टम एक रेखाखंड होता है जो मुख्य अक्ष के लंबवत होता है और किसी भी फोकस से गुजरता है और जिसके सिरे वृत्ताकार वक्र पर स्थित होते हैं (चित्र 10.26)।

चित्र 10.26
एलिप्स $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ के लेन्स रेखा की लंबाई ज्ञात करने के लिए
मान लीजिए $AF_2$ की लंबाई $l$ है।
तो $A$ के निर्देशांक $(c, l)$ है, अर्थात $(a e, l)$
क्योंकि A एलिप्स $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ पर स्थित है, हमें इस प्रकार है
$ \begin{aligned} & \dfrac{(a e)^{2}}{a^{2}}+\dfrac{l^{ 2}}{b^{2}}=1 \\
$$ \begin{aligned} & \Rightarrow l^{2}=b^{2}(1-e^{2}) \\ & \text{लेकिन} \quad \quad \quad e^{2}=\dfrac{c^{2}}{a^{2}}=\dfrac{a^{2}-b^{2}}{a^{2}}=1-\dfrac{b^{2}}{a^{2}} \end{aligned} $$
इसलिए $ \quad \quad \quad l^{2}=\dfrac{b^{4}}{a^{2}}, \text{ अर्थात, } l=\dfrac{b^{2}}{a} $
चूंकि वृत्त एक अक्ष $y$-अक्ष के संबंध में सममित है (स्पष्ट रूप से, इसके दोनों निर्देशांक अक्षों के संबंध में भी सममित है), $AF_2=F_2 B$ और इसलिए लैटस रेक्टम की लंबाई $\dfrac{2 b^{2}}{a}$ है।
उदाहरण 9 वृत्त के फोकस, शीर्ष, मुख्य अक्ष की लंबाई, न्यून अक्ष की लंबाई, विकेंद्रता और लैटस रेक्टम के निर्देशांक ज्ञात कीजिए
$ \dfrac{x^{2}}{25}+\dfrac{y^{2}}{9}=1 $
हल चूंकि $\dfrac{x^{2}}{25}$ के हर के मान के बराबर है $\dfrac{y^{2}}{9}$ के हर के मान से, मुख्य अक्ष $x$-अक्ष के अनुदिश है। दिए गए समीकरण की तुलना $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ से करते हुए, हम प्राप्त करते हैं
$ \begin{aligned} & a=5 \text{ और } b=3 . \text{ अतः } \\ & c=\sqrt{a^{2}-b^{2}}=\sqrt{25-9}=4 \end{aligned} $
इसलिए, फोकस के निर्देशांक $(-4,0)$ और $(4,0)$ हैं, शीर्ष के निर्देशांक $(-5,0)$ और $(5,0)$ हैं। मुख्य अक्ष की लंबाई 10 इकाई है, न्यून अक्ष की लंबाई $2b$ 6 इकाई है और विकेंद्रता $\dfrac{4}{5}$ है तथा लंब वृत्तलम्ब $\dfrac{2b^{2}}{a}=\dfrac{18}{5}$ है।
उदाहरण 10 वृत्त $9 x^{2}+4 y^{2}=36$ के फोकस, शीर्ष, मुख्य अक्ष और न्यून अक्ष की लंबाई और उत्केंद्रता के निर्देशांक ज्ञात कीजिए।
हल दिए गए वृत्त के समीकरण को मानक रूप में लिखा जा सकता है:
$ \dfrac{x^{2}}{4}+\dfrac{y^{2}}{9}=1 $
भी $\quad c=\sqrt{a^{2}-b^{2}}=\sqrt{9-4}=\sqrt{5}$
और $\quad e=\dfrac{c}{a}=\dfrac{\sqrt{5}}{3}$
इसलिए फोकस $(0, \sqrt{5})$ और $(0,-\sqrt{5})$ हैं, शीर्ष $(0,3)$ और $(0,-3)$ हैं, मुख्य अक्ष की लंबाई 6 इकाई है, बाहरी अक्ष की लंबाई 4 इकाई है और वृत्त की विकृति $\dfrac{\sqrt{5}}{3}$ है।
उदाहरण 11 ज्ञात कीजिए वृत्त का समीकरण जिसके शीर्ष $( \pm 13,0)$ और फोकस $( \pm 5,0)$ हैं।
हल चूंकि शीर्ष $x$-अक्ष पर हैं, इसलिए समीकरण निम्न रूप में होगा
$ \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1, \text{ जहाँ } a \text{ अर्ध-मुख्य अक्ष है। } $
दिया गया है कि $a=13, c= \pm 5$।
इसलिए, संबंध $c^{2}=a^{2}-b^{2}$ से हम प्राप्त करते हैं
$ 25=169-b^{2} \text{, अर्थात } b=12 $
इसलिए वृत्त का समीकरण $\dfrac{x^{2}}{169}+\dfrac{y^{2}}{144}=1$ है।
उदाहरण 12 मुख्य अक्ष की लंबाई 20 और फोकस $(0, \pm 5)$ वाले एक वृत्त का समीकरण ज्ञात कीजिए।
हल चूंकि फोकस $y$-अक्ष पर हैं, इसलिए मुख्य अक्ष $y$-अक्ष के अनुदिश है। इसलिए वृत्त का समीकरण निम्न रूप में होगा $\dfrac{x^{3}}{b^{2}}+\dfrac{y^{2}}{a^{2}}=1$।
दिया गया है
$ a=\text{ अर्ध-मुख्य अक्ष }=\dfrac{20}{2}=10 $
और संबंध $\quad \quad \quad c^{2}=a^{2}-b^{2}~$ देता है
$ 5^{2}=10^{2}-b^{2} ~\text{ अर्थात, } ~b^{2}=75 $
इसलिए, वृत्त का समीकरण है
$ \dfrac{x^{2}}{75}+\dfrac{y^{2}}{100}=1 $
उदाहरण 13 $x$-अक्ष के अनुदिश मुख्य अक्ष वाले एक वृत्त का समीकरण ज्ञात कीजिए जो बिंदुओं $(4,3)$ और $(-1,4)$ से गुजरता हो।
हल वृत्त के मानक रूप है $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$। चूंकि बिंदु $(4,3)$ और $(-1,4)$ वृत्त पर स्थित हैं, हमें प्राप्त होता है
$ \begin{aligned} & \quad \quad \quad \quad \dfrac{16}{a^{2}}+\dfrac{9}{b^{2}}=1 \quad \quad \quad \quad \quad \ldots (1) \\ & \text{and }\quad \quad \dfrac{1}{a^{2}}+\dfrac{16}{b^{2}}=1 \quad \quad \quad \quad \quad \ldots (2) \end{aligned} $
समीकरण (1) और (2) को हल करने पर हम ज्ञात करते हैं कि $a^{2}=\dfrac{247}{7}$ और $b^{2}=\dfrac{243}{15}$।
अतः अभीष्ट समीकरण है
$ \dfrac{x^{2}}{\left(\dfrac{247}{7}\right)}+\dfrac{y^{2}}{\dfrac{247}{15}}=1 \text{, अर्थात् } 7 x^{2}+15 y^{2}=247 $
अभ्यास 10.3
प्रत्येक अभ्यास $1$ से $9$ में, दीर्घवृत्त के फोकस, शीर्ष, मुख्य अक्ष की लम्बाई, लघु अक्ष की लम्बाई, वृत्तीय विकेन्द्रता और अपवर्तक लम्ब की लम्बाई के निर्देशांक ज्ञात कीजिए।
1. $\dfrac{x^{2}}{16}+\dfrac{y^{2}}{9}=1$
उत्तर दिखाएं
Answer :
The given equation is $\dfrac{x^{2}}{16}+\dfrac{y^{2}}{9}=1$ or $\dfrac{x^{2}}{4^{2}}+\dfrac{y^{2}}{3^{2}}=1$
Here, the denominator of $\dfrac{x^{2}}{16}$ is greater than the denominator of $\dfrac{y^{2}}{9}$
Therefore, the major axis is along the $x$-axis, while the minor axis is along the $y$-axis.
On comparing the given equation with $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$, we obtain $a=4$ and $b=3$
$\therefore \ \ c=\sqrt{a^{2}-b^{2}}=\sqrt{16-9}=\sqrt{7}$
Therefore,
The coordinates of the foci are $( \pm \sqrt{7}, 0)$
The coordinates of the vertices are $( \pm 4,0)$
Length of major axis $=2 a=8$
Length of minor axis $=2 b=6$
Eccentricity, $e=\dfrac{c}{a}=\dfrac{\sqrt{7}}{4}$
Length of latus rectum $=\dfrac{2 b^{2}}{a}=\dfrac{2 \times 9}{4}=\dfrac{9}{2}$
2. $\dfrac{x^{2}}{25}+\dfrac{y^{2}}{100}=1$
उत्तर दिखाएं
Answer :
The given equation is $\dfrac{x^{2}}{25}+\dfrac{y^{2}}{100}=1$ or $\dfrac{x^{2}}{5^{2}}+\dfrac{y^{2}}{10^{2}}=1$
Here, the denominator of $\dfrac{y^{2}}{100}$ is greater than the denominator of $\dfrac{x^{2}}{25}$
Therefore, the major axis is along the $y$-axis, while the minor axis is along the $x$-axis.
On comparing the given equation with $\dfrac{x^{2}}{b^{2}}+\dfrac{y^{2}}{a^{2}}=1$, we obtain $b=5$ and $a=10$
$\therefore \ \ c=\sqrt{a^{2}-b^{2}}=\sqrt{100-25}=\sqrt{75}=5 \sqrt{3}$
Therefore,
The coordinates of the foci are $(0, \pm 5 \sqrt{3})$
The coordinates of the vertices are $(0, \pm 10)$
Length of major axis $=2 a=20$
Length of minor axis $=2 b=10$
Eccentricity, $e=\dfrac{c}{a}=\dfrac{5 \sqrt{3}}{10}=\dfrac{\sqrt{3}}{2}$
Length of latus rectum $=\dfrac{2 b^{2}}{a}=\dfrac{2 \times 25}{10}=5$
3. $\dfrac{x^{2}}{49}+\dfrac{y^{2}}{36}=1$
उत्तर दिखाएं
उत्तर :
दिया गया समीकरण $\dfrac{x^{2}}{49}+\dfrac{y^{2}}{36}=1$ या $\dfrac{x^{2}}{7^{2}}+\dfrac{y^{2}}{6^{2}}=1$ है।
यहाँ, $\dfrac{x^{2}}{49}$ के अतिसमाक भाजक, $\dfrac{y^{2}}{36}$ के अतिसमाक भाजक से अधिक है।
इसलिए, मुख्य अक्ष $x$-अक्ष के अनुदिश है, जबकि न्यून अक्ष $y$-अक्ष के अनुदिश है।
दिए गए समीकरण को $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ के साथ तुलना करने पर, हमें $a=7$ और $b=6$ प्राप्त होते हैं।
$\therefore \ \ c=\sqrt{a^{2}-b^{2}}=\sqrt{49-36}=\sqrt{13}$
इसलिए,
फोकस के निर्देशांक $( \pm \sqrt{13}, 0)$ हैं।
शीर्ष के निर्देशांक $( \pm 7,0)$ हैं।
मुख्य अक्ष की लम्बाई $=2 a=14$
न्यून अक्ष की लम्बाई $=2 b=12$
अपसारिता, $e=\dfrac{c}{a}=\dfrac{\sqrt{13}}{7}$
लैटस रेक्टम की लम्बाई $=\dfrac{2 b^{2}}{a}=\dfrac{2 \times 36}{7}=\dfrac{72}{7}$
4. $\dfrac{x^{2}}{100}+\dfrac{y^{2}}{400}=1$
उत्तर दिखाएं
उत्तर :
दिया गया समीकरण $\dfrac{x^{2}}{100}+\dfrac{y^{2}}{400}=1$ या $\dfrac{x^{2}}{10^{2}}+\dfrac{y^{2}}{20^{2}}=1$ है।
यहाँ, $\dfrac{y^{2}}{400}$ के अतिसमाक भाजक, $\dfrac{x^{2}}{100}$ के अतिसमाक भाजक से अधिक है।
इसलिए, मुख्य अक्ष $y$-अक्ष के अनुदिश है, जबकि न्यून अक्ष $x$-अक्ष के अनुदिश है।
दिए गए समीकरण को $\dfrac{x^{2}}{b^{2}}+\dfrac{y^{2}}{a^{2}}=1$ के साथ तुलना करने पर, हमें $b=10$ और $a=20$ प्राप्त होते हैं।
$\therefore \ \ c=\sqrt{a^{2}-b^{2}}=\sqrt{400-100}=\sqrt{300}=10 \sqrt{3}$
इसलिए,
फोकस के निर्देशांक $(0, \pm 10 \sqrt{3})$ हैं।
शीर्ष के निर्देशांक $(0, \pm 20)$ हैं।
मुख्य अक्ष की लम्बाई $=2 a=40$
न्यून अक्ष की लम्बाई $=2 b=20$
अपसारिता, $e=\dfrac{c}{a}=\dfrac{10 \sqrt{3}}{20}=\dfrac{\sqrt{3}}{2}$
लैटस रेक्टम की लम्बाई $=\dfrac{2 b^{2}}{a}=\dfrac{2 \times 100}{20}=10$
7. $36 x^{2}+4 y^{2}=144$
उत्तर दिखाएं
उत्तर :
दिया गया समीकरण $36 x^{2}+4 y^{2}=144$
यह लिखा जा सकता है
$36 x^{2}+4 y^{2}=144$
या, $\dfrac{x^{2}}{4}+\dfrac{y^{2}}{36}=1$
या, $\dfrac{x^{2}}{2^{2}}+\dfrac{y^{2}}{6^{2}}=1\qquad \ldots(1)$
यहाँ, $\dfrac{y^{2}}{6^{2}}$ के हर के मान के बराबर है $\dfrac{x^{2}}{2^{2}}$ के हर के मान से अधिक है
इसलिए, मुख्य अक्ष $y$-अक्ष के अनुदिश है, जबकि न्यून अक्ष $x$-अक्ष के अनुदिश है।
समीकरण (1) की तुलना $\dfrac{x^{2}}{b^{2}}+\dfrac{y^{2}}{a^{2}}=1$ से करते हुए, हमें $b=2$ और $a=6$ प्राप्त होते हैं
$\therefore \ \ c=\sqrt{a^{2}-b^{2}}=\sqrt{36-4}=\sqrt{32}=4 \sqrt{2}$
इसलिए,
फोकस के निर्देशांक $(0, \pm 4 \sqrt{2})$ हैं
शीर्ष के निर्देशांक $(0, \pm 6)$ हैं
मुख्य अक्ष की लम्बाई $=2 a=12$
न्यून अक्ष की लम्बाई $=2 b=4$
अपसारिता, $e=\dfrac{c}{a}=\dfrac{4 \sqrt{2}}{6}=\dfrac{2 \sqrt{2}}{3}$
लैटस रेक्टम की लम्बाई $=\dfrac{2 b^{2}}{a}=\dfrac{2 \times 4}{6}=\dfrac{4}{3}$
8. $16 x^{2}+y^{2}=16$
उत्तर दिखाएं
Answer :
दिया गया समीकरण $16 x^{2}+y^{2}=16$ है
इसे लिखा जा सकता है
$16 x^{2}+y^{2}=16$
या, $\dfrac{x^{2}}{1}+\dfrac{y^{2}}{16}=1$
या, $\dfrac{x^{2}}{1^{2}}+\dfrac{y^{2}}{4^{2}}=1\qquad \ldots(1)$
यहाँ, $\dfrac{y^{2}}{4^{2}}$ के हर के मान के बराबर है $\dfrac{x^{2}}{1^{2}}$ के हर के मान से अधिक है
इसलिए, मुख्य अक्ष $y$-अक्ष के अनुदिश है, जबकि न्यून अक्ष $x$-अक्ष के अनुदिश है।
समीकरण (1) की तुलना $\dfrac{x^{2}}{b^{2}}+\dfrac{y^{2}}{a^{2}}=1$ से करते हुए, हमें $b=1$ और $a=4$ प्राप्त होते हैं
$\therefore \ \ c=\sqrt{a^{2}-b^{2}}=\sqrt{16-1}=\sqrt{15}$
इसलिए,
फोकस के निर्देशांक $(0, \pm \sqrt{15})$ हैं
शीर्ष के निर्देशांक $(0, \pm 4)$ हैं
मुख्य अक्ष की लम्बाई $=2 a=8$
न्यून अक्ष की लम्बाई $=2 b=2$
अपसारिता, $e=\dfrac{c}{a}=\dfrac{\sqrt{15}}{4}$
लैटस रेक्टम की लम्बाई $ =\dfrac{2 b^{2}}{a}=\dfrac{2 \times 1}{4}=\dfrac{1}{2} $
9. $4 x^{2}+9 y^{2}=36$
उत्तर दिखाएं
Answer :
दिया गया समीकरण $4 x^{2}+9 y^{2}=36$ है
इसे लिखा जा सकता है
$4 x^{2}+9 y^{2}=36$
या, $\dfrac{x^{2}}{9}+\dfrac{y^{2}}{4}=1$
या, $\dfrac{x^{2}}{3^{2}}+\dfrac{y^{2}}{2^{2}}=1$
यहाँ, $\dfrac{x^{2}}{3^{2}}$ के अंशक के बराबर है $\dfrac{y^{2}}{2^{2}}$ के अंशक से अधिक है
इसलिए, मुख्य अक्ष $x$-अक्ष के अनुदिश है, जबकि न्यून अक्ष $y$-अक्ष के अनुदिश है।
दिए गए समीकरण की तुलना $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ से करते हुए, हमें $a=3$ और $b=2$ प्राप्त होते हैं
$\therefore \ \ c=\sqrt{a^{2}-b^{2}}=\sqrt{9-4}=\sqrt{5}$
इसलिए,
फोकस के निर्देशांक $( \pm \sqrt{5}, 0)$ हैं
शीर्ष के निर्देशांक $( \pm 3,0)$ हैं
मुख्य अक्ष की लंबाई $=2 a=6$
न्यून अक्ष की लंबाई $=2 b=4$
अपसारिता, $e=\dfrac{c}{a}=\dfrac{\sqrt{5}}{3}$
लैटस रेक्टम की लंबाई $ =\dfrac{2 b^{2}}{a}=\dfrac{2 \times 4}{3}=\dfrac{8}{3} $
निम्नलिखित प्रश्नों 10 से 20 में से प्रत्येक में, दिए गए शर्तों को संतुष्ट करने वाले अतिपरवलय के समीकरण को ज्ञात कीजिए:
10. शीर्ष $( \pm 5,0)$, फोकस $( \pm 4,0)$
उत्तर दिखाएं
उत्तर :
शीर्ष $( \pm 5,0)$, फोकस $( \pm 4,0)$
यहाँ, शीर्ष $x$-अक्ष पर हैं।
इसलिए, अतिपरवलय का समीकरण $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ के रूप में होगा, जहाँ $a$ मुख्य अक्ष की अर्ध-लंबाई है।
इसलिए, $a=5$ और $c=4$
ज्ञात है कि $a^{2}=b^{2}+c^{2}$
$\therefore \ \ 5^{2}=b^{2}+4^{2}$
$\Rightarrow 25=b^{2}+16$
$\Rightarrow b^{2}=25-16$
$\Rightarrow b=\sqrt{9}=3$
इसलिए, अतिपरवलय का समीकरण $\dfrac{x^{2}}{5^{2}}+\dfrac{y^{2}}{3^{2}}=1$ या $\dfrac{x^{2}}{25}+\dfrac{y^{2}}{9}=1$ है।
11. शीर्ष $(0, \pm 13)$, फोकस $(0, \pm 5)$
उत्तर दिखाएं
उत्तर :
शीर्ष $(0, \pm 13)$, फोकस $(0, \pm 5)$
यहाँ, शीर्ष $y$-अक्ष पर हैं।
इसलिए, अतिपरवलय का समीकरण $\dfrac{x^{2}}{b^{2}}+\dfrac{y^{2}}{a^{2}}=1$ के रूप में होगा, जहाँ $a$ मुख्य अक्ष की अर्ध-लंबाई है।
इसलिए, $a=13$ और $c=5$
ज्ञात है कि $a^{2}=b^{2}+c^{2}$
$\therefore \ \ 13^{2}=b^{2}+5^{2}$
$\Rightarrow 169=b^{2}+25$
$\Rightarrow b^{2}=169-25$
$\Rightarrow b=\sqrt{144}=12$
इसलिए, वृत्त का समीकरण $\dfrac{x^{2}}{12^{2}}+\dfrac{y^{2}}{13^{2}}=1$ या $\dfrac{x^{2}}{144}+\dfrac{y^{2}}{169}=1$ है।
12. शीर्ष $( \pm 6,0)$, फोकस $( \pm 4,0)$
उत्तर दिखाएं
उत्तर :
शीर्ष $( \pm 6,0)$, फोकस $( \pm 4,0)$
यहाँ, शीर्ष $x$-अक्ष पर हैं।
इसलिए, वृत्त का समीकरण $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ के रूप में होगा, जहाँ $a$ अर्ध-मुख्य अक्ष है।
इसलिए, $a=6, c=4$
ज्ञात है कि $a^{2}=b^{2}+c^{2}$
$\therefore \ \ 6^{2}=b^{2}+4^{2}$
$\Rightarrow 36=b^{2}+16$
$\Rightarrow b^{2}=36-16$
$\Rightarrow b=\sqrt{20}$
इसलिए, वृत्त का समीकरण $ \dfrac{x^{2}}{6^{2}}+\dfrac{y^{2}}{(\sqrt{20})^{2}}=1 \text{ या } \dfrac{x^{2}}{36}+\dfrac{y^{2}}{20}=1 $
13. मुख्य अक्ष के सिरे $( \pm 3,0)$, लघु अक्ष के सिरे $(0, \pm 2)$
उत्तर दिखाएं
उत्तर :
मुख्य अक्ष के सिरे $( \pm 3,0)$ , लघु अक्ष के सिरे $(0, \pm 2 )$
यहाँ, मुख्य अक्ष $x$-अक्ष पर है।
इसलिए, वृत्त का समीकरण $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ के रूप में होगा, जहाँ $a$ अर्ध-मुख्य अक्ष है।
इसलिए, $a=3$ और $b=2$
इसलिए, वृत्त का समीकरण $\dfrac{x^{2}}{3^{2}}+\dfrac{y^{2}}{2^{2}}=1$ अर्थात $\dfrac{x^{2}}{9}+\dfrac{y^{2}}{4}=1$ है।
14. मुख्य अक्ष के सिरे $(0, \pm \sqrt{5})$, लघु अक्ष के सिरे $( \pm 1,0)$
उत्तर दिखाएं
उत्तर :
मुख्य अक्ष के सिरे $(0, \pm \sqrt{5})$, लघु अक्ष के सिरे $( \pm 1,0)$
यहाँ, मुख्य अक्ष $y$-अक्ष पर है।
इसलिए, वृत्त का समीकरण $\dfrac{x^{2}}{b^{2}}+\dfrac{y^{2}}{a^{2}}=1$ के रूप में होगा, जहाँ $a$ अर्ध-मुख्य अक्ष है।
इसलिए, $a=\sqrt{5}$ और $b=1$
इसलिए, वृत्त का समीकरण
$ \dfrac{x^{2}}{1^{2}}+\dfrac{y^{2}}{(\sqrt{5})^{2}}=1 \text{ या } \dfrac{x^{2}}{1}+\dfrac{y^{2}}{5}=1 `
$
15. मुख्य अक्ष की लम्बाई $26$ , फोकस $( \pm 5,0)$
उत्तर दिखाएं
उत्तर :
मुख्य अक्ष की लम्बाई $=26$; फोकस $=( \pm 5,0)$
क्योंकि फोकस $x$-अक्ष पर हैं, इसलिए मुख्य अक्ष $x$-अक्ष के अनुदिश है।
इसलिए, वृत्त के समीकरण के रूप में $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ होगा, जहाँ $a$ मुख्य अक्ष की अर्ध-लम्बाई है।
इसलिए, $2 a=26 \Rightarrow a=13$ और $c=5$
ज्ञात है कि $a^{2}=b^{2}+c^{2}$
$\therefore \ \ 13^{2}=b^{2}+5^{2}$
$\Rightarrow 169=b^{2}+25$
$\Rightarrow b^{2}=169-25$
$\Rightarrow b=\sqrt{144}=12$
इसलिए, वृत्त के समीकरण $\dfrac{x^{2}}{13^{2}}+\dfrac{y^{2}}{12^{2}}=1$ या $\dfrac{x^{2}}{169}+\dfrac{y^{2}}{144}=1$ होगा।
16. न्यूनतम अक्ष की लम्बाई $16$ , फोकस $(0, \pm 6)$
उत्तर दिखाएं
उत्तर :
न्यूनतम अक्ष की लम्बाई $=16$; फोकस $=(0, \pm 6)$
क्योंकि फोकस $y$-अक्ष पर हैं, इसलिए मुख्य अक्ष $y$-अक्ष के अनुदिश है।
इसलिए, वृत्त के समीकरण के रूप में $\dfrac{x^{2}}{b^{2}}+\dfrac{y^{2}}{a^{2}}=1$ होगा, जहाँ $a$ मुख्य अक्ष की अर्ध-लम्बाई है।
इसलिए, $2 b=16 \Rightarrow b=8$ और $c=6$
ज्ञात है कि $a^{2}=b^{2}+c^{2}$
$\therefore \ \ a^{2}=8^{2}+6^{2}=64+36=100$
$\Rightarrow a=\sqrt{100}=10$
इसलिए, वृत्त के समीकरण $\dfrac{x^{2}}{8^{2}}+\dfrac{y^{2}}{10^{2}}=1$ या $\dfrac{x^{2}}{64}+\dfrac{y^{2}}{100}=1$ होगा।
17. फोकस $( \pm 3,0), a=4$
उत्तर दिखाएं
उत्तर :
फोकस $ ( \pm 3,0), a=4$
क्योंकि फोकस $x$-अक्ष पर हैं, इसलिए मुख्य अक्ष $x$-अक्ष के अनुदिश है।
इसलिए, वृत्त के समीकरण के रूप में $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ होगा, जहाँ $a$ मुख्य अक्ष की अर्ध-लम्बाई है।
इसलिए, $c=3$ और $a=4$
ज्ञात है कि $a^{2}=b^{2}+c^{2}$
$\therefore \ \ 4^{2}=b^{2}+3^{2}$
$\Rightarrow 16=b^{2}+9$
$\Rightarrow b^{2}=16-9=7$
इसलिए, वृत्त के समीकरण $\dfrac{x^{2}}{16}+\dfrac{y^{2}}{7}=1$ होगा।
18. $b=3, c=4$, मूल बिंदु पर केंद्र; फोकस $x$ अक्ष पर है।
उत्तर दिखाएं
उत्तर :
दिया गया है $b=3, c=4$, मूल बिंदु पर केंद्र; फोकस $x$ अक्ष पर है।
क्योंकि फोकस $x$-अक्ष पर है, तो मुख्य अक्ष $x$-अक्ष के अनुदिश है।
इसलिए, वृत्त का समीकरण $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ के रूप में होगा, जहाँ $a$ मुख्य अक्ष की आधी लंबाई है।
इसलिए, $b=3, c=4$
ज्ञात है कि $a^{2}=b^{2}+c^{2}$
$\therefore \ \ a^{2}=3^{2}+4^{2}=9+16=25$
$\Rightarrow a=5$
इसलिए, वृत्त का समीकरण $\dfrac{x^{2}}{5^{2}}+\dfrac{y^{2}}{3^{2}}=1$ या $\dfrac{x^{2}}{25}+\dfrac{y^{2}}{9}=1$ होगा।
19. केंद्र $(0,0)$ पर, मुख्य अक्ष $y$-अक्ष पर है और बिंदुओं $(3,2)$ और $(1,6)$ से गुजरता है।
उत्तर दिखाएं
उत्तर :
केंद्र $(0,0)$ पर है और मुख्य अक्ष $y$-अक्ष पर है, इसलिए वृत्त का समीकरण निम्न रूप में होगा
$\dfrac{x^{2}}{b^{2}}+\dfrac{y^{2}}{a^{2}}=1 \qquad \ldots{(1)}$
जहाँ, $a$ मुख्य अक्ष की आधी लंबाई है
वृत्त बिंदुओं $(3,2)$ और $(1,6)$ से गुजरता है, इसलिए,
$ \dfrac{9}{b^{2}}+\dfrac{4}{a^{2}}=1 \qquad \ldots{(2)}$
$\dfrac{1}{b^{2}}+\dfrac{36}{a^{2}}=1 \qquad \ldots{(3)} $
समीकरण (2) और (3) को हल करने पर हमें $b^{2}=10$ और $a^{2}=40$ प्राप्त होते हैं
इसलिए, वृत्त का समीकरण $\dfrac{x^{2}}{10}+\dfrac{y^{2}}{40}=1$ या $4 x^{2}+y^{2}=40$ होगा।
20. मुख्य अक्ष $x$-अक्ष पर है और बिंदुओं $(4,3)$ और $(6,2)$ से गुजरता है।
उत्तर दिखाएं
उत्तर :
क्योंकि मुख्य अक्ष $x$-अक्ष पर है, इसलिए वृत्त का समीकरण निम्न रूप में होगा
$\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1 \qquad \ldots{(1)}$
जहाँ, $a$ मुख्य अक्ष की आधी लंबाई है
वृत्त बिंदुओं $(4,3)$ और $(6,2)$ से गुजरता है, इसलिए,
$\dfrac{16}{a^{2}}+\dfrac{9}{b^{2}}=1 \qquad \ldots{(2)}$
$ \dfrac{36}{a^{2}}+\dfrac{4}{b^{2}}=1 \qquad \ldots{(3)}$
समीकरण (2) और (3) को हल करने पर हमें $a^{2}=52$ और $b^{2}=13$ प्राप्त होते हैं
इसलिए, वृत्त के समीकरण है
$ \dfrac{x^{2}}{52}+\dfrac{y^{2}}{13}=1 \text{ या } x^{2}+4 y^{2}=52 $
10.6 हाइपरबोला
परिभाषा 7 एक हाइपरबोला एक तल में स्थित सभी बिंदुओं का समुच्चय होता है, जिनकी दो स्थिर बिंदुओं से दूरी के अंतर एक स्थिर संख्या होती है।
परिभाषा में उपयोग किए गए शब्द “अंतर” का अर्थ दूर वाले बिंदु से दूरी के अंतर के रूप में होता है। ये दो स्थिर बिंदु हाइपरबोला के दो फोकस होते हैं। फोकसों को मिलाने वाले रेखाखंड के मध्य बिंदु को हाइपरबोला के केंद्र कहते हैं। फोकसों के माध्यम से गुजरने वाली रेखा को अक्ष कहते हैं और केंद्र से गुजरती हुई तथा अक्ष के लंब रेखा को संयुग्मी अक्ष कहते हैं। हाइपरबोला द्वारा अक्ष को काटने वाले बिंदुओं को हाइपरबोला के शीर्ष कहते हैं (चित्र 10.27)।

चित्र 10.27
हम दो फोकस के बीच की दूरी को $2 c$ से दर्शाते हैं, दो शीर्षों के बीच की दूरी (अक्ष की लंबाई) को $2 a$ से दर्शाते हैं और हम $b$ को निम्नलिखित रूप में परिभाषित करते हैं:
$b=\sqrt{c^{2}-a^{2}}$
इसके अतिरिक्त $2 b$ अनुप्रस्थ अक्ष की लंबाई होती है (चित्र 10.28)।

चित्र 10.28
स्थिरांक $P_1 F_2 - P_1 F_1$ के निर्धारण के लिए :
चित्र 10.28 में बिंदु $P$ को $A$ और $B$ पर लेकर, हम निम्नलिखित प्राप्त करते हैं
$BF_1 - BF_2 = AF_2 - AF_1$ (हाइपरबोला के परिभाषा के अनुसार)
$BA + AF_1 - BF_2 = AB + BF_2 - AF_1$
अर्थात, $~AF_1 = BF_2$
इस प्रकार, $BF_1 - BF_2 = BA + AF_1 - BF_2 = BA = 2 a$
10.6.1 असंतृप्ति
परिभाषा 8 एक वृत्तखंड के जैसे, अनुपात $e = \dfrac{c}{a}$ को हाइपरबोला की असंतृप्ति कहते हैं। क्योंकि $c \geq a$, असंतृप्ति कभी एक से कम नहीं होती। असंतृप्ति के अनुसार, फोकस केंद्र से ae की दूरी पर होते हैं।
10.6.2 हाइपरबोला का मानक समीकरण
हाइपरबोला के समीकरण को सरलतम रूप से तब लिखा जा सकता है जब हाइपरबोला केंद्र मूल बिंदु पर हो और फोकस $x$-अक्ष या $y$-अक्ष पर हों। ऐसे दो संभावित आकृतियाँ चित्र 10.29 में दिखाई गई हैं।

${}$
हम चित्र 10.29(a) में दिखाए गए हाइपरबोला के समीकरण का व्युत्पन्न करेंगे जिसके फोकस $x$-अक्ष पर हों।
मान लीजिए $F_1$ और $F_2$ दीर्घवृत्त के दो नाभियाँ हैं और $O$ रेखाखंड $F_1 F_2$ का मध्य-बिंदु है। मान लीजिए $O$ मूल बिंदु है और $O$ से गुजरने वाली रेखा $F_2$ से गुजरती है जो धनात्मक $x$-अक्ष को दर्शाती है और $F_1$ से गुजरती है जो ऋणात्मक $x$-अक्ष को दर्शाती है। $O$ से गुजरने वाली रेखा जो $x$-अक्ष के लंबवत हो वह $y$-अक्ष को दर्शाती है। मान लीजिए $F_1$ के निर्देशांक $\mathbf X^{\prime}$ $(-c, 0)$ हैं और $F_2$ के निर्देशांक $(c, 0)$ हैं (चित्र 10.30)।

चित्र 10.30
$ \dfrac{c x}{a}-a=\sqrt{(x-c)^{2}+y^{2}} $
फिर वर्ग करने और अधिक सरल करने पर, हमें प्राप्त होता है
$ \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{c^{2}-a^{2}}=1 $
अर्थात, $\quad \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1 \quad$ (क्योंकि $c^{2}-a^{2}=b^{2}$ )
इसलिए, हाइपरबोला पर कोई भी बिंदु $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ को संतुष्ट करता है
विपरीत रूप से, मान लीजिए $P(x, y)$ उपरोक्त समीकरण को संतुष्ट करता है जहाँ $0 < a < c$. तब
$ y^{2}=b^{2}(\dfrac{x^{2}-a^{2}}{a^{2}}) $
इसलिए, $\quad PF_1 =+\sqrt{(x+c)^{2}+y^{2}}$
$=+\sqrt{(x+c)^{2}+b^{2}\left(\dfrac{x^{2}-a^{2}}{a^{2}}\right)}=a+\dfrac{c}{a} x$
इसी तरह, $\quad PF_2=a-\dfrac{a}{c} x$
अतिपरवलय $c > a$; और क्योंकि $P$ रेखा $x=a$ के दाहिने ओर है, $x > a, \dfrac{c}{a} x > a$. इसलिए,
$ a-\dfrac{c}{a} x \text{ नकारात्मक हो जाता है। इसलिए, } PF_2=\dfrac{c}{a} x-a \text{। } $
इसलिए $ \quad PF_1-PF_2=a+\dfrac{c}{a} x-\dfrac{c x}{a}+a=2 a $
साथ ही, ध्यान दें कि यदि $P$ रेखा $x=-a$ के बाईं ओर है, तो
$ PF_1=-\left(a+\dfrac{c}{a} x\right), PF_2=a-\dfrac{c}{
$
इस मामले में $PF_2 - PF_1 = 2 a$ होता है। अतः, कोई भी बिंदु जो $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ को संतुष्ट करता है, हाइपरबोला पर स्थित होता है।
इस प्रकार, हम निश्चित कर लेते हैं कि मूल बिंदु $(0,0)$ और अक्षांतर अक्ष $x$-अक्ष के अनुदिश होने वाली हाइपरबोला का समीकरण $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ होता है।
नोट - जब $a = b$ होता है तो वह हाइपरबोला एक समबाहु हाइपरबोला कहलाती है।
चर्चा हाइपरबोला के समीकरण से प्राप्त किए गए तथ्य के आधार पर, हम यह निष्कर्ष निकाल सकते हैं कि हाइपरबोला पर किसी भी बिंदु $(x, y)$ के लिए $\dfrac{x^{2}}{a^{2}} = 1 + \dfrac{y^{2}}{b^{2}} \geq 1$ होता है।
अर्थात, $\left|\dfrac{x}{a}\right| \geq 1$, अर्थात, $x \leq -a$ या $x \geq a$। अतः, वक्र के कोई भी भाग $x=+a$ और $x=-a$ के बीच नहीं रहता है, (अर्थात, संयुग्मी अक्ष पर कोई वास्तविक अक्षांश नहीं होता)।
उसी तरह, हम आकृति 11.31 (b) में हाइपरबोला के समीकरण को $\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1$ के रूप में निर्मित कर सकते हैं। ये दोनों समीकरण हाइपरबोला के मानक समीकरण के रूप में जाने जाते हैं।
नोट - हाइपरबोला के मानक समीकरणों में अनुप्रस्थ और संयुग्मी अक्ष निर्देशांक अक्ष होते हैं और केंद्र मूल बिंदु पर होता है। हालांकि, कोई भी दो लंबवत रेखाओं को अनुप्रस्थ और संयुग मानक अक्ष के रूप में ले सकते हैं, लेकिन ऐसे मामलों के अध्ययन उच्च वर्ग में होगा।
सामान्य अतिपरवलय के समीकरणों (चित्र 10.27) से, हम निम्नलिखित अवलोकन कर सकते हैं:
1. अतिपरवलय दोनों अक्षों के सापेक्ष सममित होता है, क्योंकि यदि $(x, y)$ एक अतिपरवलय पर बिंदु है, तो $(-x, y),(x,-y)$ और $(-x,-y)$ भी अतिपरवलय पर बिंदु होते हैं।
2. फोकस हमेशा अनुप्रस्थ अक्ष पर होते हैं। यह वह धनात्मक पद होता है जिसके हर अनुप्रस्थ अक्ष को दर्शाता है। उदाहरण के लिए, $\dfrac{x^{2}}{9}-\dfrac{y^{2}}{16}=1$
के अनुप्रस्थ अक्ष $x$-अक्ष के अनुदिश होता है और लंबाई 6 होती है, जबकि $\dfrac{y^{2}}{25}-\dfrac{x^{2}}{16}=1$
हाइपरबोला के अक्ष के अनुदिश लंबाई 10 है।
10.6.3 लैटस रेक्टम
परिभाषा 9 हाइपरबोला के लैटस रेक्टम एक रेखाखंड है जो अक्ष के लंबवत होता है और जो किसी भी फोकस से गुजरता है और जिसके सिरे हाइपरबोला पर स्थित होते हैं।
एस एलिप्स में जैसे, यह सिद्ध करना आसान है कि हाइपरबोला में लैटस रेक्टम की लंबाई $\dfrac{2 b^{2}}{a}$ होती है।
उदाहरण 14 हाइपरबोला के फोकस और शीर्षों के निर्देशांक, विकेंद्रता और लैटस रेक्टम की लंबाई ज्ञात कीजिए:
(i) $\dfrac{x^{2}}{9}-\dfrac{y^{2}}{16}=1$, $\qquad$(ii) $y^{2}-16 x^{2}=16$
हल (i) समीकरण $\dfrac{x^{2}}{9}-\dfrac{y^{2}}{16}=1$ को मानक समीकरण
$ \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1 $
से तुलना करें।
यहाँ, $a=3, b=4$ और $c=\sqrt{a^{2}+b^{2}}=\sqrt{9+16}=5$
इसलिए, फोकस के निर्देशांक $( \pm 5,0)$ हैं और शीर्ष के निर्देशांक $( \pm 3,0)$ हैं। अतः,
अपसारिकता $e=\dfrac{c}{a}=\dfrac{5}{3}$ है। अक्ष की लम्बाई $=\dfrac{2 b^{2}}{a}=\dfrac{32}{3}$
(ii) दोनों ओर 16 से विभाजित करने पर, हमें $\dfrac{y^{2}}{16}-\dfrac{x^{2}}{1}=1$ प्राप्त होता है।
तुलना समीकरण के साथ मानक समीकरण $\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1$ से, हम जानते हैं कि $a=4, b=1$ और $c=\sqrt{a^{2}+b^{2}}=\sqrt{16+1}=\sqrt{17}$।
इसलिए, फोकस के निर्देशांक $(0, \pm \sqrt{17})$ हैं और शीर्ष के निर्देशांक $(0, \pm 4)$ हैं। अतः,
अपसारिता $e=\dfrac{c}{a}=\dfrac{\sqrt{13}}{4}$। अक्ष की लम्बाई $=\dfrac{2 b^{2}}{a}=\dfrac{1}{2}$।
उदाहरण 15 फोकस $(0, \pm 3)$ और शीर्ष $(0, \pm \dfrac{\sqrt{11}}{2})$ वाले हाइपरबोला का समीकरण ज्ञात कीजिए।
हल चूंकि फोकस y-अक्ष पर हैं, अतः हाइपरबोला का समीकरण निम्न रूप का होता है $\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1$
किन्तु शीर्ष $(0, \pm \dfrac{\sqrt{11}}{2})$ हैं, अतः $a=\dfrac{\sqrt{11}}{2}$
इसके अतिरिक्त, फोकस $(0, \pm 3)$ हैं, अतः $c=3$ और $b^{2}=c^{2}-a^{2}=\dfrac{25}{4}$.
इसलिए, हाइपरबोला का समीकरण निम्न है
$ \dfrac{y^{2}}{\left(\dfrac{11}{4}\right)}-\dfrac{x^{2}}{\left(\dfrac{25}{4}\right)}=1 \text{, अर्थात् } 100 y^{2}-44 x^{2}=275 $
उदाहरण 16 ज्ञात कीजिए जहाँ फोकस $(0, \pm 12)$ हैं और लंबवत वृत्त की लम्बाई 36 है।
हल चूंकि फोकस $(0, \pm 12)$ हैं, इसलिए $c=12$ है।
लेटस रेक्टम की लंबाई $=\dfrac{2 b^{2}}{a}=36$ या $b^{2}=18 a$
$ \begin{aligned} & \text{इसलिए} \quad\quad\quad\quad c^{2}=a^{2}+b^{2} ; \text{ देता है } \\ & \quad\quad\quad\quad\quad\quad\quad\quad\quad 144=a^{3}+18 a \\ & \text{i.e., } \quad\quad\quad\quad\quad\quad\quad a^{2}+18 a-144=0, \\ & \text{तो } \quad \quad\quad\quad\quad\quad\quad a=-24,6 . \end{aligned} $
क्योंकि $a$ नकारात्मक नहीं हो सकता, हम $a=6$ लेते हैं और इसलिए $b^{2}=108$ होता है।
इसलिए, आवश्यक हाइपरबोला का समीकरण $\dfrac{y^{2}}{36}-\dfrac{x^{2}}{108}=1$, अर्थात् $3 y^{2}-x^{2}=108$ है।
अनुच्छेद 10.4
प्रत्येक अभ्यास 1 से 6 में, हाइपरबोला के फोकस, शीर्ष, उत्केंद्रता और लैटस रेक्टम की लंबाई ज्ञात कीजिए।
1. $\dfrac{x^{2}}{16}-\dfrac{y^{2}}{9}=1$
उत्तर दिखाएं
उत्तर :
दी गई समीकरण $\dfrac{x^{2}}{16}-\dfrac{y^{2}}{9}=1$ या $\dfrac{x^{2}}{4^{2}}-\dfrac{y^{2}}{3^{2}}=1$ है।
इस समीकरण को मानक हाइपरबोला समीकरण $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ के साथ तुलना करने पर,
हमें $a=4$ और $b=3$ प्राप्त होते हैं।
हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ c^{2}=4^{2}+3^{2}=25$
$\Rightarrow c=5$
इसलिए,
फोकस के निर्देशांक $\left( \pm 5,0\right)$ हैं
शीर्ष के निर्देशांक $\left( \pm 4,0\right)$ हैं
उत्केंद्रता, $e=\dfrac{c}{a}=\dfrac{5}{4}$
लैटस रेक्टम की लंबाई $=\dfrac{2 b^{2}}{a}=\dfrac{2 \times 9}{4}=\dfrac{9}{2}$
2. $\dfrac{y^{2}}{9}-\dfrac{x^{2}}{27}=1$
उत्तर दिखाएं
उत्तर :
दी गई समीकरण है
$ \dfrac{y^{2}}{9}-\dfrac{x^{2}}{27}=1 \text{ या } \dfrac{y^{2}}{3^{2}}-\dfrac{x^{2}}{\left(\sqrt{27}\right)^{2}}=1 $
इस समीकरण को मानक हाइपरबोला समीकरण $\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1$ के साथ तुलना करने पर,
हमें $a=3$ और $b=\sqrt{27}$ प्राप्त होते हैं।
हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$ \begin{aligned} & \therefore \ \ c^{2}=3^{2}+\left(\sqrt{27}\right)^{2}=9+27=36 \\ \\ & \Rightarrow c=6 \end{aligned} $
इसलिए,
फोकस के निर्देशांक $\left(0, \pm 6\right)$ हैं
शीर्ष के निर्देशांक $\left(0, \pm 3\right)$ हैं
उत्केंद्रता, $e=\dfrac{c}{a}=\dfrac{6}{3}=2$
लैटस रेक्टम की लंबाई $=\dfrac{2 b^{2}}{a}=\dfrac{2 \times 27}{3}=18$
3. $9 y^{2}-4 x^{2}=36$
उत्तर दिखाएं
उत्तर :
दी गई समीकरण $9 y^{2} - 4 x^{2}=36$ है।
इसे लिखा जा सकता है $9 y^{2} - 4 x^{2}=36$
or, $\dfrac{y^{2}}{4}-\dfrac{x^{2}}{9}=1$
or, $\dfrac{y^{2}}{2^{2}}-\dfrac{x^{2}}{3^{2}}=1\qquad\ldots\mathrm{(1)}$
समीकरण $\left(1\right)$ को मानक अतिपरवलय के समीकरण $\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1$ के साथ तुलना करते हुए,
हमें $a=2$ और $b=3$ प्राप्त होते हैं। हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ c^{2}=4+9=13$
$\Rightarrow c=\sqrt{13}$
इसलिए,
फोकस के निर्देशांक हैं $\left(0, \pm \sqrt{13}\right)$
शीर्ष के निर्देशांक हैं $\left(0, \pm 2\right)$
अपरिवर्तनीयता, $e=\dfrac{c}{a}=\dfrac{\sqrt{13}}{2}$
लैटस रेक्टम की लंबाई $ =\dfrac{2 b^{2}}{a}=\dfrac{2 \times 9}{2}=9 $
4. $16 x^{2}-9 y^{2}=576$
उत्तर दिखाएं
Answer :
दी गई समीकरण $16 x^{2} - 9 y^{2}=576$ है
इसे लिखा जा सकता है
$16 x^{2}-9 y^{2}=576$
$\Rightarrow \dfrac{x^{2}}{36}-\dfrac{y^{2}}{64}=1$
$\Rightarrow \dfrac{x^{2}}{6^{2}}-\dfrac{y^{2}}{8^{2}}=1\qquad\ldots\mathrm{(1)}$
समीकरण $\left(1\right)$ को मानक अतिपरवलय के समीकरण $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ के साथ तुलना करते हुए,
हमें $a=6$ और $b=8$ प्राप्त होते हैं। हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ c^{2}=36+64=100$
$\Rightarrow c=10$
इसलिए,
फोकस के निर्देशांक हैं $\left( \pm 10,0\right)$
शीर्ष के निर्देशांक हैं $\left( \pm 6,0\right)$
अपरिवर्तनीयता, $e=\dfrac{c}{a}=\dfrac{10}{6}=\dfrac{5}{3}$
लैटस रेक्टम की लंबाई $=\dfrac{2 b^{2}}{a}=\dfrac{2 \times 64}{6}=\dfrac{64}{3}$
5. $5 y^{2}-9 x^{2}=36$
उत्तर दिखाएं
Answer :
दी गई समीकरण $5 y^{2} - 9 x^{2}=36$ है
$\Rightarrow \dfrac{y^{2}}{\left(\dfrac{36}{5}\right)}-\dfrac{x^{2}}{4}=1$
$\Rightarrow \dfrac{y^{2}}{\left(\dfrac{6}{\sqrt{5}}\right)^{2}}-\dfrac{x^{2}}{2^{2}}=1\qquad\ldots\mathrm{(1)}$
समीकरण $\left(1\right)$ को मानक अतिपरवलय के समीकरण $\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1$ के साथ तुलना करते हुए,
हमें $a=\dfrac{6}{\sqrt{5}}$ और $b= 2.$ हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ c^{2}=\dfrac{36}{5}+4=\dfrac{56}{5}$
$\Rightarrow c=\sqrt{\dfrac{56}{5}}=\dfrac{2 \sqrt{14}}{\sqrt{5}}$
इसलिए, फोकस के निर्देशांक हैं $\left(0, \pm \dfrac{2 \sqrt{14}}{\sqrt{5}}\right)$
शीर्ष के निर्देशांक हैं $\left(0, \pm \dfrac{6}{\sqrt{5}}\right)$
अपसारता, $e=\dfrac{c}{a}=\dfrac{\left(\dfrac{2 \sqrt{14}}{\sqrt{5}}\right)}{\left(\dfrac{6}{\sqrt{5}}\right)}=\dfrac{\sqrt{14}}{3}$ $=\dfrac{2 b^{2}}{a}=\dfrac{2 \times 4}{\left(\dfrac{6}{\sqrt{5}}\right)}=\dfrac{4 \sqrt{5}}{3}$
लैटस रेक्टम की लंबाई $=\dfrac{2 b^{2}}{a}=\dfrac{2 \times 4}{\dfrac{6}{\sqrt{5}}}=\dfrac{64}{3}$
6. $49 y^{2}-16 x^{2}=784$
उत्तर दिखाएं
Answer :
दी गई समीकरण $49 y^{2} - 16 x^{2}=784$
इसे लिखा जा सकता है
$49 y^{2} - 16 x^{2}=784$
या, $\dfrac{y^{2}}{16}-\dfrac{x^{2}}{49}=1$
या, $\dfrac{y^{2}}{4^{2}}-\dfrac{x^{2}}{7^{2}}=1\qquad\ldots\mathrm{(1)}$
समीकरण $\left(1\right)$ को मानक अतिपरवलय समीकरण $\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1$ के साथ तुलना करते हुए,
हमें $a=4$ और $b=7$ प्राप्त होते हैं। हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ c^{2}=16+49=65$
$\Rightarrow c=\sqrt{65}$
इसलिए,
फोकस के निर्देशांक हैं $\left(0, \pm \sqrt{65}\right)$
शीर्ष के निर्देशांक हैं $\left(0, \pm 4\right)$
अपसारता, $e=\dfrac{c}{a}=\dfrac{\sqrt{65}}{4}$
लैटस रेक्टम की लंबाई $=\dfrac{2 b^{2}}{a}=\dfrac{2 \times 49}{4}=\dfrac{49}{2}$
प्रश्न 7 से 15 तक प्रत्येक अभ्यास में, दिए गए शर्तों को संतुष्ट करने वाले अतिपरवलय के समीकरण ज्ञात कीजिए।
7. शीर्ष $\left( \pm 2,0\right)$, फोकस $\left( \pm 3,0\right)$
उत्तर दिखाएं
Answer :
शीर्ष $\left( \pm 2,0\right)$, फोकस $\left( \pm 3,0\right)$
यहाँ, शीर्ष $x$-अक्ष पर हैं।
इसलिए, अतिपरवलय के समीकरण के रूप $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ है।
क्योंकि शीर्ष $\left( \pm 2,0\right)$ हैं, इसलिए $a=2$
क्योंकि फोकस $\left( \pm 3,0\right)$ हैं, इसलिए $c=3$
हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ 2^{2}+b^{2}=3^{2}$
$\quad b^{2}=9-4=5$
इसलिए, हाइपरबोला का समीकरण $\dfrac{x^{2}}{4}-\dfrac{y^{2}}{5}=1$ है।
8. शीर्ष $\left(0, \pm 5\right)$, फोकस $\left(0, \pm 8\right)$
उत्तर दिखाएं
उत्तर :
शीर्ष $\left(0, \pm 5\right)$, फोकस $\left(0, \pm 8\right)$
यहाँ, शीर्ष $y$-अक्ष पर हैं।
इसलिए, हाइपरबोला का समीकरण $\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1$ के रूप में है।
क्योंकि शीर्ष $\left(0, \pm 5\right), a=5$
क्योंकि फोकस $\left(0, \pm 8\right), c=8$
हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ 5^{2}+b^{2}=8^{2}$
$\quad b^{2}=64-25=39$
इसलिए, हाइपरबोला का समीकरण $\dfrac{y^{2}}{25}-\dfrac{x^{2}}{39}=1$ है।
9. शीर्ष $\left(0, \pm 3\right)$, फोकस $\left(0, \pm 5\right)$
उत्तर दिखाएं
उत्तर :
शीर्ष $\left(0, \pm 3\right)$, फोकस $\left(0, \pm 5\right)$
यहाँ, शीर्ष $y$-अक्ष पर हैं।
इसलिए, हाइपरबोला का समीकरण $\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1$ के रूप में है।
क्योंकि शीर्ष $\left(0, \pm 3\right), a=3$
क्योंकि फोकस $\left(0, \pm 5\right), c=5$
हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ 3^{2}+b^{2}=5^{2}$
$\Rightarrow b^{2}=25 - 9=16$
इसलिए, हाइपरबोला का समीकरण $\dfrac{y^{2}}{9}-\dfrac{x^{2}}{16}=1$ है।
10. फोकस $\left( \pm 5,0\right)$, अनुप्रस्थ अक्ष की लंबाई $8$ है।
उत्तर दिखाएं
उत्तर :
फोकस $\left( \pm 5,0\right),$ अनुप्रस्थ अक्ष की लंबाई $8$ है।
यहाँ, फोकस $x$-अक्ष पर हैं।
इसलिए, हाइपरबोला का समीकरण $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ के रूप में है।
क्योंकि फोकस $\left( \pm 5,0\right), c=5$
क्योंकि अनुप्रस्थ अक्ष की लंबाई $8$ है,
$2 a=8 \Rightarrow a=4$
हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ 4^{2}+b^{2}=5^{2}$
$\Rightarrow b^{2}=25 - 16=9$
तदनुसार, परवलय का समीकरण $\dfrac{x^{2}}{16}-\dfrac{y^{2}}{9}=1$ है।
11. फोकस $\left(0, \pm 13\right)$, संयुग्मी अक्ष की लंबाई $24 $ है।
उत्तर दिखाएं
उत्तर :
फोकस $\left(0, \pm 13\right)$, संयुग्मी अक्ष की लंबाई $24$ है।
यहाँ, फोकस $y$-अक्ष पर हैं।
इसलिए, परवलय का समीकरण निम्न रूप में होगा $\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1$
क्योंकि फोकस $\left(0, \pm 13\right), c=13$ हैं
क्योंकि संयुग्मी अक्ष की लंबाई $24,$
$2 b=24 \Rightarrow b=12$
हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ a^{2}+12^{2}=13^{2}$
$\Rightarrow a^{2}=169 - 144=25$
इसलिए, परवलय का समीकरण $\dfrac{y^{2}}{25}-\dfrac{x^{2}}{144}=1$ है।
12. फोकस $\left( \pm 3 \sqrt{5}, 0\right)$, लैटस रेक्टम की लंबाई $8$ है।
उत्तर दिखाएं
उत्तर :
फोकस $\left( \pm 3 \sqrt{5}, 0\right)$, लैटस रेक्टम की लंबाई $8$ है।
यहाँ, फोकस $x$-अक्ष पर हैं।
इसलिए, परवलय का समीकरण निम्न रूप में होगा $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$
क्योंकि फोकस $\left( \pm 3 \sqrt{5}, 0\right), c= \pm 3 \sqrt{5}$ हैं
लैटस रेक्टम की लंबाई $=8$
$\Rightarrow \dfrac{2 b^{2}}{a}=8$
$\Rightarrow b^{2}=4 a$
हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ a^{2}+4 a=45$
$\Rightarrow a^{2}+4 a - 45=0$
$\Rightarrow a^{2}+9 a - 5 a - 45=0$
$\Rightarrow\left(a+9\right)\left(a - 5\right)=0$
$\Rightarrow a=- 9,5$
क्योंकि $a$ धनात्मक है, $a=5$
$\therefore \ \ b^{2}=4 a=4 \times 5=20$
इसलिए, परवलय का समीकरण $\dfrac{x^{2}}{25}-\dfrac{y^{2}}{20}=1$ है।
13. फोकस $\left( \pm 4,0\right)$, लैटस रेक्टम की लंबाई $12$ है।
उत्तर दिखाएं
उत्तर :
फोकस $\left( \pm 4,0\right)$, लैटस रेक्टम की लंबाई $12$ है।
यहाँ, फोकस $x$-अक्ष पर हैं।
इसलिए, परवलय का समीकरण निम्न रूप में होगा $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$
क्योंकि फोकस $\left( \pm 4,0\right), c=4$
लेटस रेक्टम की लंबाई $=12$
$\Rightarrow \dfrac{2 b^{2}}{a}=12$
$\Rightarrow b^{2}=6 a$
हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ a^{2}+6 a=16$
$\Rightarrow a^{2}+6 a - 16=0$
$\Rightarrow a^{2}+8 a - 2 a - 16=0$
$\Rightarrow\left(a+8\right)\left(a - 2\right)=0$
$\Rightarrow a=- 8,2$
क्योंकि $a$ गैर-ऋणात्मक है, $a=2$
$\therefore \ \ b^{2}=6 a=6 \times 2=12$
इसलिए, हाइपरबोला का समीकरण $\dfrac{x^{2}}{4}-\dfrac{y^{2}}{12}=1$ है।
14. शीर्ष $\left( \pm 7,0\right), e=\dfrac{4}{3}$
उत्तर दिखाएं
उत्तर :
दिया गया है,
शीर्ष $\left( \pm 7,0\right)$,
$ e=\dfrac{4}{3} $
यहाँ, शीर्ष $x$-अक्ष पर हैं।
इसलिए, हाइपरबोला का समीकरण $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ के रूप में है।
क्योंकि शीर्ष $\left( \pm 7,0\right), a=7$
दिया गया है कि $e=\dfrac{4}{3}$
$\therefore \ \ \dfrac{c}{a}=\dfrac{4}{3} \quad[e=\dfrac{c}{a}]$
$\Rightarrow \dfrac{c}{7}=\dfrac{4}{3}$
$\Rightarrow c=\dfrac{28}{3}$
हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ 7^{2}+b^{2}=\left(\dfrac{28}{3}\right)^{2}$
$\Rightarrow b^{2}=\dfrac{784}{9}-49$
$\Rightarrow b^{2}=\dfrac{784-441}{9}=\dfrac{343}{9}$
इसलिए, हाइपरबोला का समीकरण $\dfrac{x^{2}}{49}-\dfrac{9 y^{2}}{343}=1$ है।
15. फोकस $\left(0, \pm \sqrt{10}\right)$, बिंदु $\left(2,3\right)$ से गुजरता है
उत्तर दिखाएं
उत्तर :
फोकस $\left(0, \pm \sqrt{10}\right)$, बिंदु $\left(2,3\right)$ से गुजरता है
यहाँ, फोकस $y$-अक्ष पर हैं।
इसलिए, हाइपरबोला का समीकरण $\dfrac{y^{2}}{a^{2}}-\dfrac{x^{2}}{b^{2}}=1$ के रूप में है।
क्योंकि फोकस $\left(0, \pm \sqrt{10}\right), c=\sqrt{10}$
हम जानते हैं कि $a^{2}+b^{2}=c^{2}$
$\therefore \ \ a^{2}+b^{2}=10$
$\Rightarrow b^{2}=10 - a^{2}\qquad \ldots(1)$
क्योंकि हाइपरबोला बिंदु $\left(2,3\right)$ से गुजरता है,
$\dfrac{9}{a^{2}}-\dfrac{4}{b^{2}}=1\qquad \ldots(2)$
समीकरण $\left(1\right)$ और $\left(2\right)$ से,
हम प्राप्त करते हैं, $\dfrac{9}{a^{2}}-\dfrac{4}{\left(10-a^{2}\right)}=1$
$\Rightarrow 9\left(10-a^{2}\right)-4 a^{2}=a^{2}\left(10-a^{2}\right)$
$\Rightarrow 90-9 a^{2}-4 a^{2}=10 a^{2}-a^{4}$
$\Rightarrow a^{4}-23 a^{2}+90=0$
$\Rightarrow a^{4}-18 a^{2}-5 a^{2}+90=0$
$\Rightarrow a^{2}\left(a^{2}-18\right)-5\left(a^{2}-18\right)=0$
$\Rightarrow\left(a^{2}-18\right)\left(a^{2}-5\right)=0$
$\Rightarrow a^{2}=18$ या $5$
अतिपरवलय में, $c>a$, अर्थात, $c^{2}>a^{2}$
$\therefore \ \ a^{2}=5$
$\Rightarrow b^{2}=10 - a^{2}=10 - 5=5$
इसलिए, अतिपरवलय का समीकरण $\dfrac{y^{2}}{5}-\dfrac{x^{2}}{5}=1$ है।
विविध उदाहरण
उदाहरण 17 चित्र 10.31 में दिखाए गए पराबोलिक दर्पण के फोकस की शीर्ष से दूरी $5 सेमी$ है। यदि दर्पण $45 सेमी$ गहरा है, तो दूरी $AB$ (चित्र 10.31) ज्ञात कीजिए।

चित्र 10.31
हल चूंकि फोकस से शीर्ष की दूरी $5 \text{ सेमी}$ है। हमारे पास, $a=5$ है। यदि शीर्ष को मूल बिंदु ले लिया जाए और दर्पण के अक्ष को धनात्मक $x$-अक्ष के अनुदिश ले लिया जाए, तो परवलय के अनुप्रस्थ काट का समीकरण होगा
$ \quad\quad\quad\quad\quad\quad\quad\quad\quad y^{2}=4(5) x=20 x $
ध्यान दें कि $ \quad\quad\quad\quad\quad x=45 . \text{ इसलिए } $
$ \quad\quad\quad\quad\quad\quad\quad\quad\quad y^{2}=900 $
इसलिए $ \quad\quad\quad\quad\quad\quad y= \pm 30 $
अतः $\quad\quad\quad\quad\quad\quad AB = 2y = 2 \times 30 = 60 \text{सेमी} $।
उदाहरण 18 $A$ बीम अपने छोरों पर समर्थित है जो 12 मीटर दूरी पर हैं। क्योंकि भार केंद्र पर केंद्रित है, केंद्र पर 3 सेंटीमीटर का विक्षेपण होता है और विक्षेपित बीम एक पराब्राज्य के आकार में है। केंद्र से कितनी दूरी पर विक्षेपण 1 सेंटीमीटर है?
हल मान लीजिए शीर्ष निम्नतम बिंदु पर है और अक्ष ऊर्ध्वाधर है। मान लीजिए निर्देशांक अक्ष चित्र 10.32 में दिखाए गए अनुसार चुने गए हैं।

चित्र 10.32
परवलय के समीकरण के रूप $x^{2}=4 a y$ होता है। चूंकि यह बिंदु $\left(6, \dfrac{3}{100}\right)$ से गुजरता है, हमें $(6)^{2}=4 a\left(\dfrac{3}{100}\right)$ मिलता है, अर्थात $a=\dfrac{36 \times 100}{12}=300 m$
मान लीजिए $AB$ बीम के विक्षेपण है जो $\dfrac{1}{100} m$ है। $B$ के निर्देशांक $(x, \dfrac{2}{100})$ हैं।
$ \begin{aligned} \text{अतः } \quad\quad\quad\quad\quad x^{2} & =4 \times 300 \times \dfrac{2}{100}=24 \\ \text{i.e. }\quad\quad\quad\quad\quad x & =\sqrt{24} \quad=2 \sqrt{6} \text{ मीटर }
\end{aligned} $
उदाहरण 19 $ A$ छड़ $AB$ लंबाई $15 cm$ की है जो दो निर्देशांक अक्षों के बीच इस तरह से बैठी है कि छोर $A$ $x$-अक्ष पर है और छोर $B$ $y$-अक्ष पर है। एक बिंदु $P(x, y)$ छड़ पर इस तरह लिया गया है कि $A P=6 cm$। दिखाइए कि $P$ का गुजरा एक अतिपरवलय है।
हल मान लीजिए $AB$ एक छड़ है जो चित्र 10.33 में दिखाए गए अनुसार $OX$ के साथ कोण $\theta$ बनाती है और $P(x, y)$ इस छड़ पर एक बिंदु है जो इस प्रकार है कि $\quad AP=6 \text{cm}$।

चित्र 10.33
$ \begin{aligned} & \text {क्योंकि } \quad \quad \quad\quad AB=15 \text{ सेमी, हमें प्राप्त है } \\ & \quad\quad\quad \quad\quad\quad \quad PB=9 \text{ सेमी।} \end{aligned} $
$P$ से $y$-अक्ष और $x$-अक्ष पर क्रमशः $PQ$ और $PR$ लम्ब खींचें।
From $\quad\quad\quad \quad \Delta PBQ, \cos \theta=\dfrac{x}{9}$
From $ \quad\quad\quad \quad \Delta PRA, \sin \theta=\dfrac{y}{6} $
क्योंकि $\cos ^{2} \theta+\sin ^{2} \theta=1$
$ \left(\dfrac{x}{9}\right)^{2}+\left(\dfrac{y}{6}\right)^{2}=1 `
$
या $ \quad\quad\quad \quad \dfrac{x^{2}}{81}+\dfrac{y^{2}}{36}=1 $
इसलिए $P$ का बिंदुपथ एक अतिपरवलय है।
अध्याय 10 पर अतिरिक्त अभ्यास
1. यदि एक परवलयाकार प्रतिबिम्बक $20 , \text{cm}$ व्यास और $5 , \text{cm}$ गहरा है, तो फोकस ज्ञात कीजिए।
उत्तर दिखाएं
उत्तर :
निर्देशांक तल के मूल बिंदु को परवलयाकार प्रतिबिम्बक के शीर्ष पर लिया जाता है ताकि प्रतिबिम्बक के अक्ष को धनात्मक $x$-अक्ष के अनुदिश लिया जाता है।
इसे आरेखीय रूप में निम्नलिखित तरह दर्शाया जा सकता है

परवलय का समीकरण $y^{2}=4 a x$ के रूप में है (क्योंकि यह दाहिने ओर खुलता है)।
चूंकि परवलय बिंदु $A\left(5,10\right)$ से गुजरता है,
$\Rightarrow \ \ 10^{2}=4 a\left(5\right)$
$\Rightarrow \ \ 100=20 a$
$\Rightarrow \ \ a=\dfrac{100}{20}=5$
इसलिए, परवलय का फोकस $\left(a, 0\right)=\left(5,0\right)$ है, जो व्यास के मध्य बिंदु है।
इसलिए, प्रतिबिम्बक का फोकस व्यास के मध्य बिंदु पर है।
2. एक चौथी एक परवलय के रूप में है जिसका अक्ष ऊर्ध्वाधर है। चौथी $10 , \text{m}$ ऊँची है और आधार पर $5 , \text{m}$ चौड़ी है। परवलय के शीर्ष से $2 , \text{m}$ की दूरी पर चौथी कितनी चौड़ी है?
उत्तर दिखाएं
उत्तर :
निर्देशांक तल के मूल बिंदु को चौथी के शीर्ष पर लिया जाता है ताकि इसका ऊर्ध्वाधर अक्ष धनात्मक $y$-अक्ष के अनुदिश हो।
परवलय का समीकरण $\mathrm{x}^2=4$ ay के रूप में है (क्योंकि यह ऊपर खुलता है)

चूंकि, परवलय बिंदु $\left(\dfrac{5}{2}, 10\right)$ से गुजरता है
$ \begin{aligned} & \left(\dfrac{5}{2}\right)^2=4 \mathrm{a}(10) \\ \\ & \Rightarrow \ \ \mathrm{a}=\dfrac{25}{4 \times 4 \times 10}=\dfrac{5}{32} `
\end{aligned} $
अतः, परवलय के आर्च का समीकरण है $ x^2=\dfrac{5}{8} y $
जब, $ \ \mathrm{y}=2 \mathrm{~m}$
$
\begin{aligned}
& \Rightarrow \ \ \mathrm{x}^2=\dfrac{5}{4} \\ \\
& \Rightarrow \ \ \mathrm{x}=\sqrt{\dfrac{5}{4}} \mathrm{m} \\ \\
& \therefore \ \ \mathrm{AB}=2 \times \sqrt{\dfrac{5}{4}} \mathrm{ \ m}=2 \times 1.118 \mathrm{ \ m} \text { (लगभग) }=2.23 \mathrm{m} \text { (लगभग) }
\end{aligned}
$
अतः, आर्च 2 मीटर ऊंचाई पर परवलय के शीर्ष से है, इसकी चौड़ाई लगभग $ 2.23 \mathrm{ \ m} $ है।
3. एक समान भार वाले सुस्थिर ब्रिज के केबल एक परवलय के रूप में लटकते हैं। एक सीधी रेखा जो 100 मीटर लंबी है और केबल पर लगे ऊर्ध्वाधर तारों द्वारा समर्थित है, सबसे लंबा तार 30 मीटर और सबसे छोटा तार 6 मीटर है। राजमार्ग से 18 मीटर दूर लगे तार की लंबाई ज्ञात कीजिए।
उत्तर दिखाएं
उत्तर :
केबल के सबसे कम बिंदु पर शीर्ष होता है। निर्देशांक तल के मूल बिंदु को परवलय के शीर्ष के रूप में लिया गया है, जबकि इसकी ऊर्ध्वाधर अक्ष धनात्मक $y$-अक्ष के अनुदिश होती है। इसे आरेखीय रूप में निम्नलिखित तरह दर्शाया जा सकता है

यहाँ, $AB$ और $OC$ केबल पर लगे सबसे लंबा और सबसे छोटा तार हैं, क्रमशः।
$DF$ राजमार्ग पर लगे समर्थन तार है, जो मध्य से 18 मीटर दूर है।
यहाँ, $AB=30 m, OC=6 m$, और
$ \qquad BC=\dfrac{100}{2}=50 m $
परवलय का समीकरण $x^{2}=4 a y$ के रूप में है (क्योंकि यह ऊपर की ओर खुलता है)।
बिंदु $A$ के निर्देशांक $\left(50,30 - 6\right)=\left(50,24\right)$ हैं।
क्योंकि $A\left(50,24\right)$ परवलय पर एक बिंदु है,
$\left(50\right)^{2}=4 a\left(24\right)$
$\Rightarrow \ \ a=\dfrac{50 \times 50}{4 \times 24}=\dfrac{625}{24}$
$\therefore \ \ $ परवलय का समीकरण, $x^{2}=4 \times \dfrac{625}{24} \times y \quad$ या $\quad 6 x^{2}=625 y$
बिंदु $D$ के $x$-निर्देशांक 18 है ।
अतः, $x=18$ पर,
$6\left(18\right)^{2}=625 y$
$\Rightarrow \ \ y=\dfrac{6 \times 18 \times 18}{625}$
$\Rightarrow \ \ y=3.11$ (लगभग)
$\therefore \ \ DE=3.11 m$
$D F=D E+E F=3.11 m+6 m=9.11 m$
इसलिए, माध्य रेखा से 18 मीटर दूर बाँधे गए समर्थन तार की लंबाई लगभग 9.11 मीटर है।
4. एक चौथाई वृत्त के रूप में एक चौकोर है। इसकी चौड़ाई केंद्र से 8 मीटर और ऊंचाई 2 मीटर है। एक सिरे से 1.5 मीटर दूर चौकोर की ऊंचाई ज्ञात कीजिए।
उत्तर दिखाएँ
उत्तर :
चूंकि केंद्र से चौकोर की ऊंचाई और चौड़ाई क्रमशः 2 मीटर और 8 मीटर है, इसलिए स्पष्ट है कि मुख्य अक्ष की लंबाई 8 मीटर है, जबकि अपवर्ती अक्ष की लंबाई 2 मीटर है।
निर्देशांक तल के मूल बिंदु को एल्लिप्स के केंद्र के रूप में लिया गया है, जबकि मुख्य अक्ष $x$-अक्ष के अनुदिश लिया गया है। इसलिए, अर्ध-एल्लिप्स को आरेखीय रूप से निम्नलिखित तरह दर्शाया जा सकता है

अर्ध-एल्लिप्स का समीकरण $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1, y \geq 0$ के रूप में होगा, जहाँ $a$ अपवर्ती अक्ष है। अतः,
$2 a=8 \Rightarrow \ \ a=4$
$b=2$
इसलिए, अर्ध-एल्लिप्स का समीकरण $\dfrac{x^{2}}{16}+\dfrac{y^{2}}{4}=1, y \geq 0$ है।
मान लीजिए $A$ मुख्य अक्ष पर एक बिंदु है जैसे कि $AB=1.5 m$ है।
$AC \perp OB$ खींचिए।
$O A=\left(4 - 1.5\right) m=2.5 m$
बिंदु $C$ के $x$-निर्देशांक 2.5 है।
समीकरण (1) में $x$ के मान को 2.5 से बदलकर हम प्राप्त करते हैं
$ \begin{aligned} & \qquad\dfrac{\left(2.5\right)^{2}}{16}+\dfrac{y^{2}}{4}=1 \\ \\ & \Rightarrow \ \ \dfrac{6.25}{16}+\dfrac{y^{2}}{4}=1 \\ \\ & \Rightarrow \ \ y^{2}=4\left(1-\dfrac{6.25}{16}\right) \\ \\ & \Rightarrow \ \ y^{2}=4\left(\dfrac{9.75}{16}\right) \\ \\ & \Rightarrow \ \ y^{2}=2.4375 \\ \\ `
& \Rightarrow \ \ y=1.56 \quad \text{ (लगभग) } \\ \\ & \therefore \ \ AC=1.56 मीटर \end{aligned} $
इसलिए, एक छोर से 1.5 मीटर के बिंदु पर आर्क की ऊंचाई लगभग 1.56 मीटर है।
5. एक छड़ जिसकी लंबाई 12 सेमी है, अक्षों के संपर्क में हमेशा रहती है। एक बिंदु P पर छड़ के लocus का समीकरण ज्ञात कीजिए, जो छड़ के x-अक्ष से संपर्क करने वाले सिरे से 3 सेमी दूर हो।
उत्तर दिखाएं
उत्तर :
मान लीजिए AB एक छड़ है जो OX के साथ कोण θ बनाती है और P(x, y) छड़ पर एक बिंदु है जहां AP = 3 सेमी है।
तब, PB = AB - AP = (12 - 3) सेमी = 9 सेमी [AB = 12 सेमी]
P से OY पर PQ ⊥ खींचिए और OX पर PR ⊥ खींचिए।

त्रिभुज PBQ में, cos θ = PQ / PB = x / 9
त्रिभुज PRA में, sin θ = PR / PA = y / 3
क्योंकि, sin²θ + cos²θ = 1,
(y/3)² + (x/9)² = 1
या, x²/81 + y²/9 = 1
इसलिए, छड़ पर बिंदु P के locus का समीकरण x²/81 + y²/9 = 1 है।
6. परवलय x² = 12y के शीर्ष को इसके लैटस रेक्टम के सिरों को मिलाने वाली रेखाओं द्वारा बने त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
उत्तर दिखाएं
उत्तर :
दिया गया परवलय x² = 12y है।
इस समीकरण को x² = 4ay के साथ तुलना करने पर, हमें 4a = 12 प्राप्त होता है, जिससे a = 3 प्राप्त होता है।
इसलिए, फोकस के निर्देशांक S(0, a) = S(0, 3) हैं।
मान लीजिए AB दिए गए परवलय का लैटस रेक्टम है।
दिए गए परवलय को लगभग खींचा जा सकता है

At $y=3, x^{2}=12\left(3\right) \Rightarrow \ \ x^{2}=36 \Rightarrow \ \ x= \pm 6$
$\therefore \ \ $ A के निर्देशांक $\left(- 6,3 \right),$ जबकि B के निर्देशांक $\left(6,3\right)$ हैं।
इसलिए, $\triangle O A B$ के शीर्ष $O\left(0,0\right), A\left(-6,3\right)$, और $B\left(6,3\right)$ हैं।
$ \begin{aligned} \text{ Area of } \triangle OAB & =\dfrac{1}{2}|0\left(3-3\right)+\left(-6\right)\left(3-0\right)+6\left(0-3\right)| \text{ unit }^{2} \\ \\ & =\dfrac{1}{2}|\left(-6\right)\left(3\right)+6\left(-3\right)| \text{ unit }^{2} \\ \\ & =\dfrac{1}{2}|-18-18| \text{ unit }^{2} \\ \\ & =\dfrac{1}{2}|-36| \text{ unit }^{2} \\ \\ & =\dfrac{1}{2} \times 36 \text{ unit }^{2} \\ \\ & =18 \text{ unit }^{2} \end{aligned} $
इसलिए, त्रिभुज के अभीष्ट क्षेत्रफल 18 इकाई $^{2}$ है।
7. एक आदमी एक दौड़ के मार्ग पर चलते हुए अपने से दो झंग झंग के बीच दूरी के योग हमेशा 10 मीटर होता है और दो झंग झंग के बीच दूरी 8 मीटर है। आदमी द्वारा बनाए गए पथ का समीकरण ज्ञात कीजिए।
उत्तर दिखाएं
Answer :
मान लीजिए $A$ और $B$ दो झंग झंग के स्थान हैं और $P\left(x, y\right)$ आदमी की स्थिति है। अतः, $PA+PB=10$।
हम जानते हैं कि यदि एक बिंदु एक तल में इस तरह गति करता है कि इसकी दो निश्चित बिंदुओं से दूरी के योग नियत रहता है, तो इसके पथ एक अतिपरवलय होता है और यह नियत मान अतिपरवलय के मुख्य अक्ष की लंबाई के बराबर होता है।
इसलिए, आदमी द्वारा बनाए गए पथ एक अतिपरवलय है जिसकी मुख्य अक्ष की लंबाई $10 m$ है, जबकि बिंदु $A$ और $B$ अतिपरवलय के नाभियाँ हैं।
निर्देशांक तल के मूल बिंदु को अतिपरवलय के केंद्र मानते हुए और मुख्य अक्ष को $x$-अक्ष के अनुदिश लेते हुए, अतिपरवलय को आरेखीय रूप से निम्नलिखित तरह से प्रस्तुत किया जा सकता है

अतिपरवलय का समीकरण $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ के रूप में होगा, जहाँ $a$ मुख्य अक्ष की अर्ध-लंबाई है
इसलिए, $2 a=10 \Rightarrow \ \ a=5$
फोकस के बीच की दूरी $\left(2 c\right)=8$
$\Rightarrow \ \ c=4$
संबंध $c=\sqrt{a^{2}-b^{2}}$ का उपयोग करते हुए, हम प्राप्त करते हैं
$4=\sqrt{25-b^{2}}$
$\Rightarrow \ \ 16=25-b^{2}$
$\Rightarrow \ \ b^{2}=25-16=9$
$\Rightarrow \ \ b=3$
इसलिए, आदमी द्वारा तय की गई पथ का समीकरण $\dfrac{x^{2}}{25}+\dfrac{y^{2}}{9}=1$ है।
8. एक समबाहु त्रिभुज पराबोला $y^{2}=4 ax$ में अंकित है, जहाँ एक शीर्ष पराबोला के शीर्ष पर है। त्रिभुज की भुजा की लंबाई ज्ञात कीजिए।
उत्तर दिखाएं
Answer :
मान लीजिए $OAB$ पराबोला $y^{2}=4 a x$ में अंकित समबाहु त्रिभुज है।
मान लीजिए $AB$ बिंदु $C$ पर $x$-अक्ष को काटता है।

मान लीजिए, $OC=k$
दी गई पराबोला के समीकरण से, हमें $y^{2}=4 a k \Rightarrow \ \ y= \pm 2 \sqrt{a k}$
$\therefore \ \ $ बिंदु $A$ और $B$ के संगत निर्देशांक $\left(k, 2 \sqrt{a k}\right)$, और $\left(k,-2 \sqrt{a k}\right)$ हैं
$AB=CA+CB=2 \sqrt{a k}+2 \sqrt{a k}=4 \sqrt{a k}$
क्योंकि $O A B$ एक समबाहु त्रिभुज है, $O A^{2}=A B^{2}$.
$ \begin{aligned} & \therefore \ \ k^{2}+\left(2 \sqrt{a k}\right)^{2}=\left(4 \sqrt{a k}\right)^{2} \\ \\ & \Rightarrow \ \ k^{2}+4 a k=16 a k \\ \\ & \Rightarrow \ \ k^{2}=12 a k \\ \\ & \Rightarrow \ \ k=12 a \\ \\ & \therefore \ \ AB=4 \sqrt{a k}=4 \sqrt{a \times 12 a}=4 \sqrt{12 a^{2}}=8 \sqrt{3} a \end{aligned} $
इसलिए, पराबोला $y^{2}=4$ ax में अंकित समबाहु त्रिभुज की भुजा $8 \sqrt{3} a$ है।
सारांश
इस अध्याय में निम्नलिखित अवधारणाओं और सामान्यीकरणों का अध्ययन किया गया है।
-
एक वृत्त एक तल में एक निश्चित बिंदु से समान दूरी पर स्थित सभी बिंदुओं के समुच्चय होता है।
-
केंद्र $(h, k)$ और त्रिज्या $r$ वाले एक वृत्त का समीकरण है
$ \qquad (x-h)^{2}+(y-k)^{2}=r^{2} . $
-
एक परवलय एक तल में स्थित सभी बिंदुओं का समुच्चय होता है जो एक निश्चित रेखा और तल में एक निश्चित बिंदु से समान दूरी पर होते हैं।
-
एक परवलय के समीकरण जिसका फोकस $(a, 0)$, $a>0$ पर हो और नियतांक $x=-a$ हो, निम्नलिखित होता है
$ \qquad y^{2}=4 a x $
-
परवलय के लैटस रेक्टम एक रेखाखंड होता है जो परवलय के अक्ष के लंबवत होता है, फोकस से गुजरता है और जिसके सिरे परवलय पर स्थित होते हैं।
-
परव लय $y^{2}=4 a x$ के लैटस रेक्टम की लंबाई $4 a$ होती है।
-
एक वृत्त एक तल में स्थित सभी बिंदुओं का समुच्चय होता है, जिनके दो निश्चित बिंदुओं से दूरी का योग एक निश्चित स्थिरांक होता है।
-
$x$-अक्ष पर फोकस वाले एलिप्स के समीकरण $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ है।
-
एलिप्स के लैटस रेक्टम एक रेखाखंड है जो केंद्र से गुजरता है और मुख्य अक्ष के लंबवत होता है, जिसके सिरे एलिप्स पर स्थित होते हैं।
-
एलिप्स $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ के लैटस रेक्टम की लंबाई $\dfrac{2 b^{2}}{a}$ है।
-
एलिप्स की विकेंद्रता एलिप्स के केंद्र से एक फोकस तक की दूरी और एक शीर्ष बिंदु तक की दूरी के अनुपात होती है।
-
एक हाइपरबोला एक तल में स्थित सभी बिंदुओं का समुच्चय होता है, जिनकी दो स्थिर बिंदुओं से दूरी के अंतर एक स्थिर संख्या होती है।
-
$x$-अक्ष पर फोकस वाली हाइपरबोला का समीकरण होता है : $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$
-
हाइपरबोला के लैटस रेक्टम एक रेखाखंड होता है जो अनुप्रस्थ अक्ष के लंबवत होता है और जो किसी भी फोकस से गुजरता है तथा जिसके सिरे हाइपरबोला पर स्थित होते हैं।
-
हाइपरबोला $: \dfrac{x^{2}}{a^{2}}-\dfrac{y बराबर 1$ के लैटस रेक्टम की लंबाई होती है : $\dfrac{2 b^{2}}{a}$।
-
एक हाइपरबोल के असंतुलितता (eccentricity) को एक हाइपरबोल के केंद्र से एक फोकस तक की दूरी और एक शीर्ष बिंदु से केंद्र तक की दूरी के अनुपात के रूप में परिभाषित किया जाता है।
ऐतिहासिक टिप्पणी
ज्यामिति गणित के सबसे प्राचीन शाखाओं में से एक है। ग्रीक ज्यामितीय विद्वानों ने कई वक्रों के गुणों की अध्ययन किया जो सिद्धांतिक और व्यावहारिक रूप से महत्वपूर्ण हैं। यूक्लिड ने लगभग 300 ईसा पूर्व में अपनी ज्यामिति के ग्रंथ की रचना की। वह पहले व्यक्ति थे जिन्होंने भौतिक विचारों के आधार पर कुछ अक्षय अक्षमों के आधार पर ज्यामितीय आकृतियों को संगठित किया। ज्यामिति के आरंभिक अध्ययन भारतीय और ग्रीक प्राचीन लोगों द्वारा किया गया जिन्होंने बीजगणित के प्रक्रिया का कोई उपयोग नहीं किया। यूक्लिड और सुल्बसुत्र आदि द्वारा ज्यामिति के विषय के संश्लेषण अनुपात के रूप में लगभग 1300 वर्ष तक जारी रहे। ईसा पूर्व 200 में एपोलोनियस ने एक किताब ‘The Conic’ की रचना की जो वृत्तीय अनुप्रस्थ खंडों के बारे में थी जिसमें कई महत्वपूर्ण खोजें शामिल थीं जो 18 शताब्दियों तक अप्रतिस्पर्धी रहीं।
Modern analytic geometry is called ‘Cartesian’ after the name of Rene Descartes (1596-1650) whose relevant ‘La Geometrie’ was published in 1637. But the fundamental principle and method of analytical geometry were already discovered by Pierre de Fermat (1601-1665). Unfortunately, Fermats treatise on the subject, entitled Ad Locus Planos et So LIDOS Isagoge (Introduction to Plane and Solid Loci) was published only posthumously in 1679. So, Descartes came to be regarded as the unique inventor of the analytical geometry.
Isaac Barrow ने कार्टेशियन विधि का उपयोग बर्बाद कर दिया। न्यूटन ने अनिर्धारित गुणांक विधि का उपयोग करके वक्रों के समीकरण खोजे। उन्होंने विभिन्न प्रकार के निर्देशांक शामिल किए, जिनमें ध्रुवीय और द्विध्रुवीय निर्देशांक शामिल थे। लेब्निज ने ‘अभिसारी’ (abscissa), ‘अक्षीय’ (ordinate) और ‘निर्देशांक’ (coordinate) शब्दों का उपयोग किया। ल’ हॉपिटल (लगभग 1700) ने विश्लेषणात्मक ज्यामिति पर एक महत्वपूर्ण पाठक की रचना की।
क्लेरॉ (1729) ने पहले दूरी सूत्र को दिया, लेकिन इसका रूप असंगत था। वह लीनियर समीकरण के अपवाद रूप को भी दिया। क्रेमर (1750) ने दो अक्षों के आधिकारिक उपयोग को दिया और एक वृत्त के समीकरण को इस तरह दिया:
$ (y-a)^{2}+(b-x)^{2}=r $
उसने अपने समय के विश्लेषणात्मक ज्यामिति के सर्वोत्तम समझाइए। मंगे (1781) ने रेखा के समीकरण के आधुनिक ‘बिंदु-ढ़ोल’ रूप को इस तरह दिया:
$ y-y^{\prime}=a(x-x^{\prime}) $
और दो रेखाओं के लंबवत होने की शर्त के रूप में $a a^{\prime}+1=0$ दिया।
एस. एफ. लाक्रॉइक्स (1765-1843) एक उत्पादक पाठक लेखक थे, लेकिन उनके विश्लेषणात्मक ज्यामिति के योगदान विभिन्न स्थानों पर फैले हुए मिलते हैं। उन्होंने रेखा के ‘दो बिंदु’ रूप के समीकरण को इस तरह दिया:
$ y-\beta=\dfrac{\beta^{\prime}-\beta}{\alpha^{\prime}-\alpha}(x-\alpha)
$
और बिंदु $(\alpha, \beta)$ से रेखा $y=a x+b$ पर लम्ब की लम्बाई $\dfrac{(\beta-a-b)}{\sqrt{1+a^{2}}}$ होती है।
दो रेखाओं के बीच कोण ज्ञात करने के लिए उसके सूत्र के अनुसार $\tan \theta=\left(\dfrac{a^{\prime}-a}{1+a a^{\prime}}\right)$. यह आश्चर्यजनक है कि एनालिटिक ज्यामिति के आविष्कार के 150 साल बाद भी ऐसी मूलभूत सूत्र की खोज करनी पड़ती है। 1818 में, सिविल इंजीनियर सी. लामे ने दो बिंदुओं के प्रतिच्छेद बिंदुओं के माध्यम से गुजरने वाली वक्र के रूप में $m E+m^{\prime} E^{\prime}=0$ दिया।
कई महत्वपूर्ण खोजें, गणित और विज्ञान दोनों में, वृत्तीय खंडों से जुड़ी हैं। ग्रीक लोग विशेष रूप से आर्किमिडीज (287-212 ई.पू.) और अपोलोनियस (200 ई.पू.) ने इन वक्रों के अपने सुंदरता के कारण अध्ययन किया। ये वक्र वर्तमान समय में बाहरी अंतरिक्ष के अन्वेषण और परमाणु कणों के व्यवहार के अनुसंधान में महत्वपूर्ण उपकरण हैं।





