हमारे पिछले अध्ययन से हम जानते हैं कि तरल और गैसें बहाव की क्षमता के कारण द्रव्य बुलाए जाते हैं। इन दोनों अवस्थाओं में द्रव्यता के कारण अणु स्वतंत्र रूप से गति कर सकते हैं। विपरीत, ठोस में संघटक कणों के स्थिर स्थान होते हैं और वे केवल अपने माध्य स्थान के आसपास आवर्ती गति कर सकते हैं। इसके कारण ठोस में कठोरता होती है। इन गुणों की विशिष्टता संघटक कणों की प्रकृति और उनके बीच कार्य करने वाले बंधन बलों पर निर्भर करती है। संरचना और गुणों के बीच संबंध अभी तक अभीष्ट गुणों वाले नए ठोस वस्तुओं की खोज में सहायता करता है। उदाहरण के लिए, कार्बन नैनोट्यूब नए वस्तुओं हैं जो इस तरह के वस्तुओं के उत्पादन के लिए अपेक्षित हैं जो स्टील से बल्बर हों, एल्यूमिनियम से हल्के हों और कॉपर से अधिक चालक हों। ऐसे वस्तुएं भविष्य में विज्ञान और समाज के विकास में बढ़ती हुई भूमिका निभा सकती हैं। कुछ अन्य वस्तुएं जो भविष्य में महत्वपूर्ण भूमिका निभाने के लिए अपेक्षित हैं, उदाहरण के लिए उच्च तापमान अत्यधिक चालक, चुंबकीय वस्तुएं, पैकेजिंग के लिए बायोडिग्रेडेबल पॉलीमर, सर्जिकल इम्प्लांट के लिए बायोकम्प्लियंट ठोस आदि हैं। इसलिए, इस अवस्था के अध्ययन की अब अधिक महत्व हो रहा है।

इस इकाई में, हम विभिन्न कणों के संभावित व्यवस्थाओं के बारे में चर्चा करेंगे जो कई प्रकार के संरचनाओं के निर्माण करते हैं और जानेंगे कि विभिन्न संरचनात्मक इकाइयों के विभिन्न व्यवस्थाएं कैसे ठोसों के विभिन्न गुणों को प्रदान करती हैं। हम इसके अलावा भी सीखेंगे कि इन गुणों में कैसे परिवर्तन होता है जब संरचनात्मक असंपूर्णताओं या अत्यंत छोटी मात्रा में अशुद्धियों की उपस्थिति के कारण होता है।

1.1 ठोस अवस्था के सामान्य गुण

कक्षा XI में आप ने सीखा होगा कि पदार्थ ठोस, तरल और गैस तीन अवस्थाओं में विद्यमान हो सकता है। तापमान और दबाव के एक निश्चित सेट के अंतर्गत, एक दिए गए पदार्थ की सबसे स्थायी अवस्था कौन सी होगी, इसके लिए दो विरोधाभासी कारकों के नेट प्रभाव पर निर्भर करता है। ये अणुओं के बीच बल जो अणुओं (या परमाणुओं या आयनों) को निकट रखने की ओर ले जाते हैं, और तापीय ऊर्जा जो अणुओं को दूर रखने की ओर ले जाती है और उन्हें तेजी से गति करने के लिए प्रेरित करती है। पर्याप्त निम्न तापमान पर, तापीय ऊर्जा कम होती है और अणुओं के बीच बल उन्हें इतना निकट लाते हैं कि वे एक दूसरे के आकर्षित हो जाते हैं और निश्चित स्थानों पर बस जाते हैं। इन अणुओं के अपने माध्य स्थान के चारों ओर अभी भी झूल सकते हैं और पदार्ोस अवस्था में रहता है।

सॉलिड स्थिति के निम्नलिखित विशिष्ट गुण हैं:

• (i) वे निश्चित द्रव्यमान, आयतन और आकार के होते हैं।
• (ii) अणुओं के बीच दूरी छोटी होती है।
• (3) अणुओं के बीच बल तीव्र होते हैं।
• (iv) उनके संघटक कण (अणु, अणु या आयन) निश्चित स्थिति में होते हैं और अपने माध्य स्थिति के चारों ओर केवल झूल सकते हैं।
• (v) वे अपस्थापनीय और अस्थाई होते हैं।

1.2 अमोर्फस और क्रिस्टलीय सॉलिड

सॉलिड को अपने संघटक कणों के व्यवस्था में उपस्थित आदेश के प्रकार के आधार पर क्रिस्टलीय या अमोर्फस के रूप में वर्गीकृत किया जा सकता है। एक क्रिस्टलीय सॉलिड आमतौर पर एक बड़ी संख्या में छोटे क्रिस्टलों से बना होता है, जिनमें से प्रत्येक के निश्चित विशिष्ट ज्यामितीय आकार होता है। क्रिस्टल में संघटक कणों (अणु, अणु या आयन) की व्यवस्था तीन आयामों में क्रमबद्ध और पुनरावृत्ति होती है। यदि हम क्रिस्टल के किसी क्षेत्र में पैटर्न को देखते हैं, तो हम क्रिस्टल के किसी भी अन्य क्षेत्र में कणों की स्थिति का ठीक तौर पर अनुमान लगा सकते हैं, चाहे वे देखे गए क्षेत्र से कितनी दूर हों। इस प्रकार, क्रिस्टल में लंबी दूरी का आदेश होता है, जिसका अर्थ है कि कणों की व्यवस्था के नियमित पैटर्न के अंतर्गत पूरे क्रिस्टल में आवर्ती रूप से दोहराया जाता है। सोडियम क्लोराइड और क्वार्ट्ज क्रिस्टलीय सॉलिड के प्रमुख उदाहरण हैं। ग्लास, रबर और कई प्लास्टिक अपने तरल ठंढ़ा होकर ठोस बनाने पर क्रिस्टल नहीं बनते। इन्हें अमोर्फस सॉलिड कहा जाता है। शब्द “अमोर्फस” ग्रीक शब्द “अमॉर्फोस” से आया है, जिसका अर्थ है कोई आकार नहीं। ऐसे सॉलिड में संघटक कणों (अणु, अणु या आयन) की व्यवस्था केवल छोटी दूरी के आदेश के रूप में होती है। ऐसी व्यवस्था में, छोटी दूरी के लिए नियमित और आवर्ती पैटर्न का अवलोकन किया जा सकता है। नियमित पैटर्न बिखरे हुए होते हैं और व्यवस्था के बीच अव्यवस्थित होती है। क्वार्ट्ज (क्रिस्टलीय) और क्वार्ट्ज ग्लास (अमोर्फस) के संरचना क्रमशः चित्र 1.1 (a) और (b) में दिखाए गए हैं।

दोनों संरचनाएं लगभग समान हैं, लेकिन अमोर्फस क्वार्टज ग्लास के मामले में लंबी दूरी की क्रमबद्धता नहीं होती। अमोर्फस ठोसों की संरचना तरल पदार्थ की संरचना के समान होती है। संघटक कणों के व्यवस्था में अंतर के कारण, दो प्रकार के ठोस एक दूसरे से अपनी गुणों में भिन्न होते हैं।

क्रिस्टलीय ठोस एक तीव्र गलनांक बिंदु पर गलते हैं। एक विशिष्ट तापमान पर वे अचानक गल जाते हैं और तरल बन जाते हैं। दूसरी ओर, अमोर्फस ठोस तापमान के एक श्रेणी के भीतर नरम हो जाते हैं, गल जाते हैं और विस्तारित होने लगते हैं और विभिन्न आकारों में ढाले जा सकते हैं। अमोर्फस ठोस तरल पदार्थ के समान संरचनात्मक विशेषताओं के साथ होते हैं और बहुत भिगोई तरल के रूप में आसानी से देखे जा सकते हैं। वे कुछ तापमान पर क्रिस्टलीय हो सकते हैं। कुछ प्राचीन सभ्यताओं के ग्लास वस्तुएं अपने दिखावे में दूध जैसी दिखाई देती हैं क्योंकि कुछ क्रिस्टलीयकरण हो जाता है। तरल पदार्थ की तरह, अमोर्फस ठोस धीरे-धीरे बहने की प्रवृत्ति रखते हैं। इसलिए, कभी-कभी इन्हें अपरिपूर्ण ठोस या अत्यधिक ठंडे तरल के रूप में बुलाया जाता है।

अमोर्फस ठोस पदार्थ प्रकृति में एकसमान होते हैं। उनके गुण, जैसे मैकेनिकल सtrength, अपवर्तनांक और विद्युत चालकता आदि, सभी दिशाओं में समान होते हैं। इसका कारण यह है कि इनमें कोई लंबी दूरी की क्रम नहीं होती है और कणों की व्यवस्था सभी दिशाओं में निश्चित नहीं होती है। इसलिए, समग्र व्यवस्था सभी दिशाओं में समान हो जाती है। इसलिए, किसी भी भौतिक गुण का मान सभी दिशाओं में समान होता है।

क्रिस्टलीय ठोस पदार्थ प्रकृति में अनिसीय होते हैं, अर्थात, उनके कुछ भौतिक गुणों जैसे विद्युत प्रतिरोध या अपवर्तनांक एक ही क्रिस्टल में विभिन्न दिशाओं में मापे जाने पर अलग-अलग मान दिखाई देते हैं। इसका कारण विभिन्न दिशाओं में कणों के अलग-अलग व्यवस्था होती है। इसका चित्र चित्र 1.2 में दिखाया गया है। यह चित्र दो तरह के परमाणुओं के व्यवस्था के एक सरल द्विविमीय पैटर्न को दिखाता है। यह चित्र में दिखाए गए दो दिशाओं में यांत्रिक गुण जैसे कटाव के तनाव के प्रति प्रतिरोध बहुत अलग हो सकते हैं। CD दिशा में विकृति वह पंक्ति को विस्थापित करती है जिसमें दो प्रकार के परमाणु होते हैं जबकि AB दिशा में एक प्रकार के परमाणुओं से बनी पंक्तियों को विस्थापित करती है। क्रिस्टलीय ठोस और अक्रिस्टलीय ठोस के बीच अंतर तालिका 1.1 में सारांशित किया गया है।

अतिरिक्त क्रिस्टलीय और अक्रिस्टलीय ठोस के अलावा, कुछ ठोस ऐसे भी होते हैं जो सतह पर अक्रिस्टलीय दिखाई देते हैं लेकिन विशिष्ट विषम अवयवों के संरचना वाले होते हैं। इन्हें बहुक्रिस्टलीय ठोस कहते हैं। धातुएं अक्सर बहुक्रिस्टलीय अवस्था में पाई जाती हैं। व्यक्तिगत क्रिस्टल यादृच्छिक दिशा में उपस्थित होते हैं ताकि धातु के नमूने को एकसमान दिखाई दे सके चाहे एकल क्रिस्टल अनिसोट्रोपिक होता है।

1.3 क्रिस्टलीय ठोसों का वर्गीकरण

अनुच्छेद 1.2 में हमने अमोर्फस पदार्थों के बारे में सीखा है और उनके केवल छोटे रेंज के क्रम के बारे में बताया गया है। हालांकि, अधिकांश ठोस पदार्थ क्रिस्टलीय प्रकृति के होते हैं। उदाहरण के लिए, लौह, तांबा और चांदी जैसे सभी धातु तत्व; फॉस्फोरस, आयोडीन जैसे अधातु तत्व और सोडियम क्लोराइड, जिंक सल्फाइड और नाफ्थलीन जैसे यौगिक क्रिस्टलीय ठोस बनाते हैं।

क्रिस्टलीय ठोस विभिन्न तरीकों से वर्गीकृत किए जा सकते हैं। विधि उद्देश्य पर निर्भर करती है। यहाँ, हम क्रिस्टलीय ठोस को उन अंतरमोलेकुलर बलों या बंधनों पर आधारित वर्गीकृत करेंगे जो घटक कणों को एक साथ बांधे रखते हैं। ये हैं — (i) वैन डर वाल्स बल; (ii) आयनिक बंध; (iii) सहसंयोजक बंध; और (iv) धातुई बंध। इस आधार पर, क्रिस्टलीय ठोस को चार श्रेणियों में वर्गीकृत किया जाता है, अर्थात, अणुक, आयनिक, धातुई और सहसंयोजक ठोस। अब हम इन श्रेणियों के बारे में जानेंगे।

1.3.1 अणुक ठोस

अणु अणुक ठोस के संघटक कण होते हैं। ये निम्नलिखित श्रेणियों में विभाजित किए जा सकते हैं:

(i) अधिर अणुक ठोस: ये या तो परमाणु, उदाहरण के लिए, आर्गन और हीलियम या अधिर सहसंयोजक बंधन द्वारा बने अणु, उदाहरण के लिए, H₂, Cl₂ और I₂ से बने होते हैं। इन ठोसों में, परमाणु या अणु के बीच कमजोर विस्थापन बल या लंडन बल होते हैं, जिसके बारे में आप कक्षा XI में सीख चुके होंगे। ये ठोस नरम होते हैं और विद्युत के चालक नहीं होते। ये निम्न गलनांक वाले होते हैं और कमरे के तापमान और दबाव पर आमतौर पर तरल या गैसीय अवस्था में पाए जाते हैं।

(ii) ध्रुवीय अणु ठोस: HCl, SO2 आदि जैसे पदार्थों के अणु ध्रुवीय सहसंयोजक बंधनों से बने होते हैं। ऐसे ठोसों में अणु अपेक्षाकृत तीव्र द्विध्रुव-द्विध्रुव परस्पर क्रिया द्वारा एक दूसरे से बंधे रहते हैं। ये ठोस नरम होते हैं और विद्युत के चालक नहीं होते। इनके गलनांक अध्रुवीय अणु ठोसों के गलनांक से अधिक होते हैं, लेकिन अधिकांश ऐसे ठोस तापमान और दबाव के अंतर्गत गैस या तरल होते हैं। ठोस SO2 और ठोस NH3 इस प्रकार के ठोसों के कुछ उदाहरण हैं।

(iii) हाइड्रोजन बंधित अणु ठोस: ऐसे ठोसों के अणु H और F, O या N परमाणुओं के बीच ध्रुवीय सहसंयोजक बंधन से बने होते हैं। मजबूत हाइड्रोजन बंधन ऐसे ठोसों के अणुओं को जैसे H2O (बर्फ) के रूप में बांधे रखते हैं। ये विद्युत के चालक नहीं होते। आमतौर पर ये तापमान और दबाव के अंतर्गत वाष्पशील तरल या नरम ठोस होते हैं।

1.3.2 आयनिक ठोस

आयन आयनिक ठोस के संघटक कण होते हैं। ऐसे ठोस तीन आयामी व्यवस्था में आयनों के बीच तीव्र आकर्षण (विद्युत स्थैतिक) बलों द्वारा बंधे आयनों से बने होते हैं। ये ठोस कठिन और टूटने वाले प्रकृति के होते हैं। इनके उच्च गलनांक और क्वथनांक होते हैं। चूंकि आयन स्वतंत्र रूप से गमन नहीं कर सकते, इनके ठोस अवस्था में विद्युत के अचालक होते हैं। हालांकि, गलित अवस्था में या पानी में घुले हुए रूप में आयन स्वतंत्र रूप से गमन कर सकते हैं और विद्युत का सुचालक बन जाते हैं।

1.3.3 धात्विक ठोस

धातुएं धनात्मक आयनों के क्रमबद्ध संग्रह होते हैं, जो एक समुद्र के रूप में घूमते आवेशहीन इलेक्ट्रॉनों द्वारा घेरे और बरकरार रखे जाते हैं। इन इलेक्ट्रॉनों की गतिशीलता होती है और उनका वितरण क्रिस्टल में समान रूप से होता है। प्रत्येक धातु अणु इस गतिशील इलेक्ट्रॉन के समुद्र में एक या एक से अधिक इलेक्ट्रॉन योगदान देता है। ये गतिशील आवेशहीन इलेक्ट्रॉन धातुओं की उच्च विद्युत और ऊष्मा चालकता के लिए जिम्मेदार होते हैं। जब विद्युत क्षेत्र लगाया जाता है, तो ये इलेक्ट्रॉन धनात्मक आयनों के नेटवर्क में बहते हैं। इसी तरह, जब धातु के एक भाग में ऊष्मा दी जाती है, तो इलेक्ट्रॉन इस ऊष्मा को एक समान रूप से वितरित करते हैं। धातुओं के एक अन्य महत्वपूर्ण गुण उनका चमक और कुछ मामलों में रंग होता है। इसका कारण भी इनमें उपस्थित गतिशील इलेक्ट्रॉनों के कारण होता है। धातुएं बहुत मृदु और तार बनाने योग्य होती हैं।

1.3.4 सहसंयोजक या नेटवर्क ठोस

क्रिस्टलीय ठोसों के एक विस्तृत वर्ग के नॉन-मेटल के बीच सहसंयोजक बंधन के निर्माण से बनते हैं। इन्हें बृहत अणु भी कहते हैं। सहसंयोजक बंधन प्रबल और दिशात्मक प्रकृति के होते हैं, इसलिए अणु अपने स्थान पर बहुत मजबूत रूप से बरकरार रहते हैं। ऐसे ठोस बहुत कठिन और टूटने वाले होते हैं। इनके गलनांक बहुत उच्च होते हैं और गलन से पहले वे तोड़ जाते हैं। ये विद्युत के चालक नहीं होते हैं। हीरा (चित्र 1.3) और सिलिकॉन कार्बाइट ऐसे ठोसों के प्रमुख उदाहरण हैं। भले ही ग्राफाइट (चित्र 1.4) इस वर्ग के क्रिस्टल के अंतर्गत आता है, लेकिन यह नरम होता है और विद्युत का चालक होता है। इसके अद्वितीय गुण इसकी सामान्य संरचना के कारण होते हैं। कार्बन अणु विभिन्न परतों में व्यवस्थित होते हैं और प्रत्येक अणु अपनी एक ही परत में तीन अपने पड़ोसी अणुओं से सहसंयोजक बंधन से जुड़ा होता है। प्रत्येक अणु के चौथा संयोजकता इलेक्ट्रॉन विभिन्न परतों के बीच होता है और यह आवागमन के लिए मुक्त होता है। इन मुक्त इलेक्ट्रॉनों के कारण ग्राफाइट विद्युत का अच्छा चालक होता है। विभिन्न परतें एक दूसरे के ऊपर फिसल सकती हैं। इस कारण ग्राफाइट एक नरम ठोस और एक अच्छा ठोस घर्षण विरोधी होता है।

अंतर्गत प्रश्न

1.5 निम्नलिखित ठोसों को उनमें कार्य करने वाले अंतरमोलेकुलर बल के प्रकार के आधार पर विभिन्न श्रेणियों में वर्गीकृत करें: पोटेशियम सल्फेट, टिन, बेंज़ीन, यूरिया, अमोनिया, पानी, जिंक सल्फाइड, ग्राफाइट, रबीडियम, आर्गन, सिलिकॉन कार्बाइड।

उत्तर दिखाएं

उत्तर

पोटेशियम सल्फेट $\rightarrow$ आयनिक ठोस

टिन $\rightarrow$ धातुई ठोस

बेंज़ीन $\rightarrow$ आणविक (अध्रुवीय) ठोस

यूरिया $\rightarrow$ ध्रुवीय आणविक ठो स

अमोनिया $\rightarrow$ ध्रुवीय आणविक ठोस

पानी $\rightarrow$ हाइड्रोजन बंधित आणविक ठोस

जिंक सल्फाइड $\rightarrow$ आयनिक ठोस

ग्राफाइट $\rightarrow$ सहसंयोजक या नेटवर्क ठोस

रबीडियम $\rightarrow$ धातुई ठोस

आर्गन $\rightarrow$ अध्रुवीय आणविक ठोस

सिलिकॉन कार्बाइड $\rightarrow$ सहसंयोजक या नेटवर्क ठोस

1.6 ठोस A एक बहुत कठिन विद्युत अपचालक है, जो ठोस अवस्था में भी तथा विलयन अवस्था में भी अत्यधिक उच्च तापमान पर पिघलता है। इस ठोस के प्रकार क्या है?

उत्तर दिखाएं

उत्तर

दिए गए गुण एक सहसंयोजक या नेटवर्क ठोस के गुण हैं। अतः दिए गए ठोस के प्रकार सहसंयोजक या नेटवर्क ठोस है। ऐसे ठोसों के उदाहरण डायमंड (C) और क्वार्टज $\left(\mathrm{SiO}_{2}\right)$ हैं।

1.7 आयनिक ठोस विलयन अवस्था में विद्युत का चालन करते हैं लेकिन ठोस अवस्था में नहीं। समझाइए।

उत्तर दिखाएं

उत्तर

आयनिक यौगिकों में विद्युत का चालन आयनों द्वारा होता है। ठोस अवस्था में, आयन तीव्र विद्युत आकर्षण बलों द्वारा एक दूसरे से बंधे होते हैं और ठोस के भीतर गति करने के लिए मुक्त नहीं होते हैं। अतः आयनिक ठोस ठोस अवस्था में विद्युत का चालन नहीं करते हैं। हालांकि, विलयन अवस्था में या विलयन रूप में, आयन मुक्त रूप से गति करते हैं और विद्युत का चालन कर सकते हैं।

1.8 विद्युत चालक, खींचने योग्य और खोदने योग्य ठोस किस प्रकार के होते हैं?

उत्तर दिखाएं

उत्तर

धातुई ठोस विद्युत के चालक होते हैं, आघात विरोधी तथा तार विरोधी होते हैं।

1.4 क्रिस्टल लैटिस और इकाई कोशिका

आप निश्चित रूप से देख चुके होंगे कि जब टाइल फर्श को कवर करने के लिए रखी जाती हैं, तो एक दोहरा पैटर्न बनता है। यदि फर्श पर टाइल रख दें और सभी टाइलों में एक ही स्थान पर एक बिंदु चिह्नित कर दें (जैसे कि टाइल के केंद्र) और टाइल को नजरअंदाज करते हुए केवल चिह्नित स्थानों को देखें, तो हमें बिंदुओं का एक सेट मिलता है। इस बिंदुओं के सेट को एक संरचनात्मक इकाई के रूप में रखकर पैटर्न के विकास के लिए आधार के रूप में ले लिया जाता है। यह आधार एक स्थानीय लैटिस है जिस पर दो-विमीय पैटर्न के विकास के लिए इसके बिंदुओं पर संरचनात्मक इकाइयों को रखा जाता है (जैसे कि इस मामले में टाइल)।

संरचनात्मक इकाई को आधार या मोटिफ कहते हैं। जब मोटिफ को स्पेस लैटिस के बिंदुओं पर रखा जाता है, तो एक पैटर्न बनता है। क्रिस्टल संरचना में, मोटिफ एक अणु, परमाणु या आयन होता है। स्पेस लैटिस, जिसे क्रिस्टल लैटिस भी कहते हैं, इन मोटिफ के स्थान को दर्शाने वाला बिंदुओं का पैटर्न होता है। अन्य शब्दों में, स्पेस लैटिस क्रिस्टल संरचना के एक अमूर्त संरचना होती है। जब हम स्पेस लैटिस के बिंदुओं पर मोटिफ को एक जैसे ढंग से रखते हैं, तो हमें क्रिस्टल संरचना प्राप्त होती है। चित्र 1.5 में एक मोटिफ, एक द्विविमीय लैटिस और एक अनुमानित द्विविमीय क्रिस्टल संरचना को दर्शाया गया है, जिसे द्विविमीय लैटिस में मोटिफ को रखकर प्राप्त किया गया है।

संरचना बिंदुओं के स्थानीय व्यवस्था विभिन्न प्रकार के लैटिस के उत्पन्न करती है। चित्र 1.6 दो अलग-अलग लैटिस में बिंदुओं की व्यवस्था को दर्शाता है। क्रिस्टलीय ठोस के मामले में, स्थान लैटिस एक तीन-आयामी बिंदुओं की सारणी होती है। क्रिस्टल संरचना को लैटिस बिंदुओं के साथ संरचनात्मक मोटिफ के संबंध द्वारा प्राप्त किया जाता है। प्रत्येक दोहराए गए आधार या मोटिफ की संरचना एवं स्थानीय दिशा क्रिस्टल में अन्य मोटिफ के समान होती है। क्रिस्टल के पूरे भाग में प्रत्येक मोटिफ के परिवेश समान होता है, सतह के अतिरिक्त।

एक क्रिस्टल लैटिस के गुण निम्नलिखित हैं: (a) एक लैटिस में प्रत्येक बिंदु को लैटिस बिंदु या लैटिस साइट कहा जाता है। (b) एक क्रिस्टल लैटिस में प्रत्येक बिंदु एक संघटक कण को दर्शाता है जो एक परमाणु, एक अणु (परमाणुओं का समूह) या आयन हो सकता है। (c) लैटिस बिंदुओं को सीधी रेखाओं द्वारा जोड़कर लैटिस के ज्यामिति को दिखाया जाता है।

हमें केवल क्रिस्टल के स्पेस लैटिस के एक छोटे हिस्से की आवश्यकता होती है ताकि क्रिस्टल को पूरी तरह से निर्दिष्ट किया जा सके। इस छोटे हिस्से को यूनिट सेल कहते हैं। एक यूनिट सेल कई तरीकों से चुना जा सकता है। सामान्यतः वह सेल चुनी जाती है जिसकी भुजाएँ लंबवत होती हैं और सबसे छोटी लंबाई की होती हैं और एक तीन आयामी अनुवादी विस्थापन द्वारा यूनिट सेल के पुनरावर्ती विस्थापन से पूरा क्रिस्टल बनाया जा सकता है। चित्र 1.7 में एक द्विआयामी लैटिस के यूनिट सेल के विस्थापन को दिखाया गया है जिससे पूरा क्रिस्टल संरचना बनाई जा सकती है। इसके अलावा, यूनिट सेल के आकार इस प्रकार होते हैं कि ये सेलों के बीच के अंतर के बिना पूरे लैटिस को भर देते हैं।

द्वि-विमानी अवलोकन में, एक विपरीत चतुर्भुज जिसकी भुजाओं की लंबाई ‘a’ और ‘b’ है और इन भुजाओं के बीच कोण r है, इकाई सेल के रूप में चुनी जाती है। द्वि-विमानी में संभावित इकाई सेल के चित्र 1.8 में दिखाए गए हैं।

तीन-विमानी क्रिस्टल संरचना में, इकाई सेल द्वारा निर्धारित होता है:

तीन-विमानी क्रिस्टल लैटिस के एक भाग और इसका इकाई सेल चित्र 1.9 में दिखाए गए हैं।

तीन-विमानी क्रिस्टल संरचना में, इकाई सेल द्वारा निर्धारित होता है:

(i) तीन भुजाओं a, b और c के अनुदिश आकार। इन भुजाओं एक दूसरे के लंब न हो सकती हैं या हो सकती हैं।

(ii) किनारों के बीच कोण, a (b और c के बीच), b (a और c के बीच) और g (a और b के बीच)। इस प्रकार, एक इकाई सेल को छह पैरामीटरों a, b, c, a , b और g द्वारा विशेषता रखा जाता है। एक सामान्य इकाई सेल के इन पैरामीटरों को चित्र 1.6 में दिखाया गया है।

1.4.1 प्रामाणिक और केंद्रित इकाई सेल

इकाई सेल को दो विस्तारों में विभाजित किया जा सकता है, प्रामाणिक और केंद्रित इकाई सेल।

(a) प्रामाणिक यूनिट सेल: जब एक यूनिट सेल के कोनों पर ही घटक कण (परमाणु, अणु या आयन) उपस्थित हों, तो इसे प्रामाणिक यूनिट सेल कहते हैं।

(b) केंद्रित यूनिट सेल: जब एक यूनिट सेल में कोनों पर उपस्थित घटक कणों के अतिरिक्त एक या एक से अधिक घटक कण अन्य स्थानों पर उपस्थित हों, तो इसे केंद्रित यूनिट सेल कहते हैं। केंद्रित यूनिट सेल तीन प्रकार के होते हैं:

(i) बॉडी-केंद्रित यूनिट सेल: ऐसी यूनिट सेल में अपने बॉडी केंद्र पर एक घटक कण (परमाणु, अणु या आयन) के अतिरिक्त अपने कोनों पर उपस्थित घटक कण भी होते हैं।

(ii) फेस-सेंट्रेड यूनिट सेल: ऐसे यूनिट सेल में, प्रत्येक फेस के केंद्र में एक संघटक कण उपस्थित होता है, अपने कोनों में उपस्थित कणों के अतिरिक्त।

(iii) एंड-सेंट्रेड यूनिट सेल: ऐसे यूनिट सेल में, कोनों में उपस्थित कणों के अतिरिक्त, किसी दो विपरीत फेसों के केंद्र में एक संघटक कण उपस्थित होता है।

अनेक प्रकार के क्रिस्टलों की जांच करने पर निष्कर्ष निकलता है कि सभी क्रिस्टलों को एक से एक सात नियमित आकृतियों में से किसी एक के अनुरूप माना जा सकता है। इन आधार नियमित आकृतियों को सात क्रिस्टल प्रणालियाँ कहते हैं। एक दिए गए क्रिस्टल किस प्रणाली में आता है, इसका निर्धारण उसके फेसों के बीच कोणों के मापन और उसके आकार के मुख्य विशेषताओं को परिभाषित करने के लिए कितने अक्षों की आवश्यकता होती है इस बात पर आधारित होता है। चित्र 1.11 सात क्रिस्टल प्रणालियों को दिखाता है।

एक फ्रांसीसी गणितज्ञ, ब्रॉवेस, ने दिखाया कि केवल 14 संभव तीन-आयामी जाल हो सकते हैं। इन्हें ब्रॉवेस जाल कहते हैं। इन जालों के इकाई सेल निम्नलिखित बॉक्स में दिखाए गए हैं। इनके प्राथमिक इकाई सेल के विशेषताओं के साथ उनके बना सकने वाले सेंट्रेड इकाई सेल के बारे में तालिका 1.3 में सूचीबद्ध किया गया है।

1.5 एकक कोश में परमाणुओं की संख्या

हम जानते हैं कि कोई भी क्रिस्टल जालक बहुत बड़ी संख्या में एकक कोशों से बना होता है और प्रत्येक जालक बिंदु एक संघटक कण (परमाणु, अणु या आयन) द्वारा घेरा रहता है। अब हम ज्ञात करेंगे कि प्रत्येक कण के कितने भाग एक विशिष्ट एकक कोश के स्वामी होते हैं।

हम तीन प्रकार के घन एकक कोश के बारे में विचार करेंगे और सरलता के लिए मान लेंगे कि संघटक कण एक परमाणु है।

प्रामाणिक घनीय एकक कोष्ठ में केवल कोनों पर परमाणु होते हैं। प्रत्येक कोने पर परमाणु आठ समीपवर्ती एकक कोष्ठों के बीच साझा होता है, जैसा कि चित्र 1.12 में दिखाया गया है। चार एकक कोष्ठ एक ही स्तर में और चार एकक कोष्ठ ऊपरी (या नीचे की) स्तर में होते हैं। अतः, केवल एक आठवाँ भाग परमाणु (या अणु या आयन) एक विशिष्ट एकक कोष्ठ के स्वामी होता है। चित्र 1.13 में, एक प्रामाणिक घनीय एकक कोष्ठ तीन अलग-अलग तरीकों से दिखाया गया है। चित्र 1 बी 13 (ए) में प्रत्येक छोटे गोला केवल उस स्थिति में उपस्थित पार्टिकल के केंद्र को निरूपित करता है और नहीं उसके वास्तविक आकार को। ऐसे संरचनाएँ खुले संरचनाओं के रूप में जानी जाती हैं। खुले संरचनाओं में कणों के व्यवस्था को आसानी से अनुसरण किया जा सकता है। चित्र 1.13 (बी) में एकक कोष्ठ के वास्तविक कण आकार के साथ स्थान भरने वाला निरूपण दिखाया गया है और चित्र 1.13 (सी) में घनीय एकक कोष्ठ में उपस्थित विभिन्न परमाणुओं के वास्तविक भाग दिखाए गए हैं।

सभी में, क्योंकि प्रत्येक घन एकक कोष्ठ में 8 परमाणु कोनों पर होते हैं, एक एकक कोष्ठ में कुल परमाणुओं की संख्या 8 × 1/8 = 1 परमाणु होती है।

1.5.2 बॉडी सेंट्रेड क्यूबिक एकक कोष्ठ

एक शरीर केंद्रित घन (bcc) एकक कोष्ठ में प्रत्येक कोने पर एक परमाणु तथा शरीर केंद्र पर एक परमाणु होता है। चित्र 1.14 में (a) खुला संरचना (b) स्थान भरने वाला मॉडल तथा (c) एकक कोष्ठ के भागों के साथ एकक कोष्ठ को दर्शाया गया है। यह देखा जा सकता है कि शरीर केंद्र पर विद्यमान परमाणु उस एकक कोष्ठ के लिए पूरी तरह से स्वामी होता है। अतः एक शरीर केंद्रित घन (bcc) एकक कोष्ठ में:

(i) 8 कोने × प्रत्येक कोने परमाणु के लिए 1/8 = 8 × 1/8 = 1 परमाणु

(ii) 1 शरीर केंद्र परमाणु = 1 × 1 = 1 परमाणु \ एकक कोष्ठ में कुल परमाणु संख्या = 2 परमाणु

1.5.3 फेस-सेंट्रेड क्यूबिक यूनिट सेल

एक फेस-सेंट्रेड क्यूबिक (fcc) यूनिट सेल में कोनों और क्यूब के सभी फेस के केंद्र पर परमाणु होते हैं। चित्र 1.15 में देखा जा सकता है कि प्रत्येक फेस केंद्र पर स्थित परमाणु दो समीपवर्ती यूनिट सेलों के बीच साझा होते हैं और प्रत्येक परमाणु केवल एक यूनिट सेल के लिए 1/2 हिस्सा से संबंधित होता है। चित्र 1.16 में (a) खुला संरचना (b) स्थान भरने वाला मॉडल और (c) वास्तव में इस यूनिट सेल के हिस्से के साथ यूनिट सेल को दर्शाया गया है। इस प्रकार, एक फेस-सेंट्रेड क्यूबिक (fcc) यूनिट सेल में:

(i) 8 कोने के परमाणु × 1/8 परमाणु प्रति एकक कोश = 8 × 1/8 = 1 परमाणु

(ii) 6 फेस-सेंटर्ड परमाणु × 1/2 परमाणु प्रति एकक कोश = 6 × 1/2 = 3 परमाणु

प्रति एकक कोश में कुल परमाणु संख्या = 4 परमाणु

अंतर्गत प्रश्न

1.9 ‘लेटिस पॉइंट’ के महत्व को समझाइए।

उत्तर दिखाएँ

उत्तर

लेटिस पॉइंट के महत्व यह है कि प्रत्येक लेटिस पॉइंट एक ठोस के एक संघटक कण को प्रतिनिधित्व करता है जो एक परमाणु, एक अणु (परमाणु के समूह) या आयन हो सकता है।

1.10 एक एकक कोष्ठ को चरित्र करने वाले पैरामीटर के नाम बताइए।

उत्तर दिखाएँ

उत्तर

एक एकक कोष्ठ को चरित्र करने वाले छह पैरामीटर निम्नलिखित हैं।

(i) तीन किनारों के अनुदिश आयाम, $a, b$ और $c$

इन किनारों के बराबर हो सकते हैं या नहीं।

(ii) किनारों के बीच कोण

इन कोण $\propto$ (किनारों b और c के बीच), (किनारों a और c के बीच), और (किनारों a और b के बीच) हैं

1.11 अंतर करें

(i) षट्कोणीय और एकांकी एकक कोष्ठ

(ii) चेहरा केंद्रित और सिरा केंद्रित एकक कोष्ठ।

उत्तर दिखाएँ

उत्तर

(i) षट्कोणीय एकक कोष्ठ

एक षट्कोणीय एकक कोष्ठ के लिए,

$a=b \neq c$

और $\alpha=\beta=90^{\circ}$

$\gamma=120^{\circ}$

एकांकी एकक कोष्ठ

एक एकांकी कोष्ठ के लिए,

$a \neq b \neq c$

और $\alpha=\gamma=90^{\circ}$

$\beta \neq 90^{\circ}$

(ii) चेहरा केंद्रित एकक कोष्ठ

एक चेहरा केंद्रित एकक कोष्ठ में, संघटक कण कोर के तथा प्रत्येक चेहरे के केंद्र में एक होते हैं।

सिरा केंद्रित एकक कोष्ठ

एक सिरा केंद्रित एकक कोष्ठ में कण कोर में होते हैं और किसी दो विपरीत सिरों के केंद्र में एक होता है।

1.12 समझाइए कि एक घन एकक कोष्ठ के कोने और शरीर केंद्र पर स्थित एक परमाणु के कितने भाग उसके पड़ोसी एकक कोष्ठ के हिस्सा होते हैं।

उत्तर दिखाएँ

उत्तर

(i) एक घन एकक कोष्ठ के कोने पर स्थित एक परमाणु आठ पड़ोसी एकक कोष्ठों द्वारा साझा किया जाता है।

इसलिए, एक एकक कोष्ठ के लिए परमाणु का 1/8 भाग साझा किया जाता है।

(ii) एक घन एकक कोष्ठ के शरीर केंद्र पर स्थित एक परमाणु उसके पड़ोसी एकक कोष्ठों द्वारा साझा नहीं किया जाता है। इसलिए, यह परमाणु केवल उस एकक कोष्ठ में होता है जिसमें यह स्थित है, अर्थात इसका एकक कोष्ठ के लिए योगदान 1 होता है।

1.6 सघन ढेरी वाले संरचनाएँ

ठोस में, संघटक कण सघन ढेरी में होते हैं, जिससे न्यूनतम रिक्त स्थान बचता है। हम इन संघटक कणों को समान गोलियों के रूप में मानकर तीन चरणों में तीन आयामी संरचना के निर्माण की चर्चा करेंगे।

(a) एक आयाम में सघन ढेरी एक आयाम में गोलियों के सघन ढेरी के व्यवस्था करने के केवल एक तरीका होता है, अर्थात उन्हें एक पंक्ति में रखकर एक दूसरे के संपर्क में रखा जाता है (चित्र 1.17)।

इस व्यवस्था में, प्रत्येक गोली अपने दो आस-पास के पड़ोसियों के संपर्क में होती है। एक कण के सबसे करीब के पड़ोसियों की संख्या को उसकी संयोजन संख्या कहते हैं। इस प्रकार, एक आयामी संपूर्ण व्यवस्था में, संयोजन संख्या 2 होती है।

(b) दो आयामों में संपूर्ण व्यवस्था

दो आयामी संपूर्ण संरचना को निकटतम व्यवस्था वाली गोलियों के पंक्तियों के स्टैकिंग (स्थापन) द्वारा उत्पन्न किया जा सकता है। इसे दो अलग-अलग तरीकों से किया जा सकता है।

(i) दूसरी पंक्ति को पहली पंक्ति के संपर्क में रखा जा सकता है ताकि दूसरी पंक्ति की गोलियाँ पहली पंक्ति की गोलियों के ठीक ऊपर हों। दोनों पंक्तियों की गोलियाँ क्षैतिज रूप से भी एवं ऊर्ध्वाधर रूप से भी समानांतर होती हैं। यदि हम पहली पंक्ति को ‘A’ प्रकार की पंक्ति कहें, तो दूसरी पंक जो पहली पंक्ति के ठीक जैसी होती है, वह भी ‘A’ प्रकार की होती है। इसी तरह, हम अधिक पंक्तियाँ रखकर AAA प्रकार की व्यवस्था प्राप्त कर सकते हैं, जैसा कि चित्र 1.18 (a) में दिखाया गया है।

इस व्यवस्था में, प्रत्येक गोला अपने चार आसपास के पड़ोसियों के संपर्क में होता है। इसलिए, द्विविमीय समन्वय संख्या 4 होती है। इसके अतिरिक्त, यदि इन 4 तुरंत पड़ोसी गोलों के केंद्रों को जोड़ दिया जाए, तो एक वर्ग बनता है। इसलिए इस व्यवस्था को द्विविमीय वर्गीय संकुलित व्यवस्था कहा जाता है।

(ii) द्वितीय पंक्ति को पहली पंक्ति के ऊपर एक ढलान वाले ढंग से रखा जा सकता है ताकि इसके गोले पहली पंक्ति के घरों में फिट कर सकें। यदि पहली पंक्ति में गोलों की व्यवस्था को ‘A’ प्रकार कहा जाए, तो द्वितीय पंक्ति में गोलों की व्यवस्था अलग होती है और इसे ‘B’ प्रकार कहा जा सकता है। जब तीसरी पंक्ति को द्वितीय पंक्ति के ऊपर ढलान वाले ढंग से रखा जाता है, तो इसके गोले पहली पंक तक अलाइन हो जाते हैं। इसलिए इस पंक्ति को भी ‘A’ प्रकार कहा जा सकता है। इसी ढंग से रखी गई चौथी पंक्ति के गोले द्वितीय पंक्ति के गोलों (जो ‘B’ प्रकार के होते हैं) के साथ अलाइन होते हैं। इसलिए इस व्यवस्था को ABAB प्रकार कहा जाता है। इस व्यवस्था में कम रिक्त स्थान होता है और यह व्यवस्था वर्गीय संकुलित व्यवस्था की तुलना में अधिक कुशल होती है। प्रत्येक गोला अपने छ: पड़ोसियों के संपर्क में होता है और द्विविमीय समन्वय संख्या 6 होती है। इन छ: गोलों के केंद्र एक नियमित षष्टकोण के कोनों पर होते हैं (चित्र 1.18 b) इसलिए इस व्यवस्था को द्विविमीय षष्टकोणीय संकुलित व्यवस्था कहा जाता है। चित्र 1.18 (b) में देखा जा सकता है कि इस परत में कुछ रिक्त स्थान (खाली स्थान) होते हैं। ये त्रिकोणीय आकार के होते हैं। त्रिकोणीय रिक्त स्थान दो अलग-अलग प्रकार के होते हैं। एक पंक्ति में त्रिकोण के शिखर ऊपर की ओर बिंदु बनाते हैं और अगली पंक्ति में नीचे की ओर बिंदु बनाते हैं।

(c) तीन आयामों में सघन ढेलाई

सभी वास्तविक संरचनाएँ तीन आयामी संरचनाएँ होती हैं। ये द्वि-आयामी तलों के एक ऊपर दूसरे के ऊपर ढेलाई करके प्राप्त की जा सकती हैं। पिछले अनुच्छेद में हम द्वि-आयामी सघन ढेलाई के बारे में चर्चा कर चुके हैं जो दो प्रकार की हो सकती है; वर्ग सघन ढेलाई और षट्कोणीय सघन ढेलाई। अब हम इनके आधार पर कौन से प्रकार की तीन आयामी सघन ढेलाई प्राप्त की जा सकती है इसकी जांच करें।

(i) तीन-विमीय सघन पैकिंग द्वि-विमीय वर्ग सघन पैकिंग लेयर बनाती है: जब दूसरी वर्ग सघन पैकिंग लेयर पहली लेयर के ऊपर रखी जाती है, तो हम उसी नियम का पालन करते हैं जो एक पंक्ति के दूसरे पंक्ति के साथ रखे जाने के दौरान अपनाया गया था। दूसरी लेयर पहली लेयर के ऊपर रखी जाती है ताकि ऊपरी लेयर के गोले पहली लेयर के गोलों के ठीक ऊपर हों। इस व्यवस्था में, दोनों लेयर के गोले क्षैतिज रूप से भी एवं ऊर्ध्वाधर रूप से भी पूर्णतः संरेखित होते हैं, जैसा कि चित्र 1.19 में दिखाया गया है। इसी तरह, हम एक दूसरे के ऊपर अधिक लेयर रख सकते हैं। यदि पहली लेयर में गोलों की व्यवस्था ‘A’ प्रकार की कहलाती है, तो सभी लेयरों की व्यवस्था एक जैसी होती है। इसलिए इस लैटिस का पैटर्न AAA… प्रकार का होता है। इस तरह उत्पन्न लैटिस सरल घन लैटिस होता है, और इसका एकक कोष्ठक प्राथमिक घन एकक कोष्ठक होता है (चित्र 1.19 देखें)।

(ii) द्वि-विमीय षष्टीय व्यवस्था वाले तलों से त्रि-विमीय घनत्व वाली संरचना: त्रि-विमीय घनत्व वाली संरचना को एक दूसरे के ऊपर रखे गए तलों के माध्यम से बनाया जा सकता है।

(a) पहले तल पर दूसरे तल को रखना

मान लीजिए कि हम एक द्वि-विमीय षष्टीय व्यवस्था वाला तल ‘A’ लेते हैं और इसके ऊपर एक समान तल रखते हैं ताकि दूसरे तल के गोले पहले तल के घर्षणों में रखे गए हों। क्योंकि दोनों तलों के गोले अलग-अलग व्यवस्था में हैं, इसलिए दूसरे तल को ब नाम दें। आकृति 1.20 से यह देखा जा सकता है कि पहले तल के सभी त्रिकोणीय रिक्त स्थान दूसरे तल के गोलों द्वारा ढक नहीं लिए जाते हैं। इससे विभिन्न व्यवस्थाएं उत्पन्न होती हैं। जहां दूसरे तल का एक गोला पहले तल के रिक्त स्थान के ऊपर होता है (या उलटा), तो एक चतुष्कोणीय रिक्त स्थान बनता है। इन रिक्त स्थानों को चतुष्कोणीय रिक्त स्थान कहा जाता है क्योंकि इन चार गोलों के केंद्रों को मिलाने पर एक चतुष्कोण बनता है। इन रिक्त स्थानों को आकृति 1.20 में ‘T’ के रूप में चिह्नित किया गया है। एक ऐसा रिक्त स्थान आकृति 1.21 में अलग से दिखाया गया है।

अन्य स्थानों पर, दूसरे परत में त्रिकोणीय रिक्त स्थान पहले परत में त्रिकोणीय रिक्त स्थानों के ऊपर होते हैं, और इनके त्रिकोणीय आकार एक दूसरे के ऊपर नहीं आते। इनमें से एक के त्रिकोण के शिखर ऊपर की ओर बिंदु बताते हैं और दूसरे के नीचे की ओर बिंदु बताते हैं। इन रिक्त स्थानों को चित्र 1.20 में ‘O’ के रूप में चिह्नित किया गया है। ऐसे रिक्त स्थान छह गोलियों द्वारा घिरे होते हैं और इन्हें अष्टफलकीय रिक्त स्थान कहा जाता है। एक ऐसा रिक्त स्थान चित्र 1.21 में अलग से दिखाया गया है। इन दो प्रकार के रिक्त स्थानों की संख्या संकीर्ण ढेर गोलियों की संख्या पर निर्भर करती है।

मान लीजिए कि कुछ समीपतम पैक किए गए गोलियों की संख्या N है, तो: अष्टफलक रिक्तियों की संख्या = N त्रिकोणी रिक्तियों की संख्या = 2N

(b) दूसरे तल पर तीसरे तल को रखना

जब तीसरे तल को दूसरे तल पर रखा जाता है, तो दो संभावनाएँ हो सकती हैं।

(i) त्रिकोणी रिक्तियों को ढँकना: दूसरे तल के त्रिकोणी रिक्तियों को तीसरे तल के गोलियों द्वारा ढँका जा सकता है। इस स्थिति में, तीसरे तल के गोलियाँ पहले तल के गोलियों के साथ ठीक एक रेखा में समानांतर होती हैं। इस प्रकार, गोलियों के पैटर्न के विकल्प तलों में दोहराया जाता है। इस पैटर्न को आमतौर पर ABAB ……. पैटर्न के रूप में लिखा जाता है। यह संरचना अष्टफलकीय सघन पैक की संरचना (hcp संरचना) कहलाती है (चित्र 1.22)। ऐसी परमाणु संरचना कई धातुओं में पाई जाती है, जैसे मैग्नीशियम और जिंक।

(ii) अष्टफलक रिक्त स्थान के ऊपर ढकना: दूसरे तल के ऊपर तीसरा तल इस तरह रखा जा सकता है कि इसके गोले अष्टफलक रिक्त स्थान को ढके। जब इस तरह रखा जाता है, तो तीसरे तल के गोले पहले या दूसरे तल के गोलों के साथ समानांतर नहीं होते। इस व्यवस्था को ‘C’ प्रकार कहा जाता है। केवल जब चौथा तल रखा जाता है, तो इसके गोले पहले तल के गोलों के साथ समानांतर हो जाते हैं, जैसा कि चित्र 1.22 और 1.23 में दिखाया गया है। इस प्रकार के तलों के पैटर्न को अक्सर ABCABC ……….. के रूप में लिखा जाता है। यह संरचना घनीय संकेंद्रित (ccp) या फेस-सेंटर्ड क्यूबिक (fcc) संरचना के रूप में जानी जाती है। तांबा और चांदी जैसे धातुएं इस संरचना में क्रिस्टलीकृत होती हैं।

दोनों प्रकार के सघन पैकिंग बहुत कुशल होते हैं और क्रिस्टल में 74% स्थान भर जाता है। इनमें से किसी भी में, प्रत्येक गोला बारह गोलों के संपर्क में होता है। इसलिए, इन दोनों संरचनाओं में संयोजन संख्या 12 होती है।

1.6.1 यौगिक का सूत्र और भरे गए रिक्त स्थानों की संख्या

पहले इस अनुच्छेद में हमने सीखा था कि जब कण सघन पैक किए जाते हैं जिसके परिणामस्वरूप ccp या hcp संरचना बनती है, तो दो प्रकार के रिक्त स्थान उत्पन्न होते हैं। जबकि एक लैटिस में अष्टफलकीय रिक्त स्थानों की संख्या सघन पैक किए गए कणों की संख्या के बराबर होती है, तेत्रफलकीय रिक्त स्थानों की संख्या इसकी दोगुनी होती है। आयनिक ठोस में, बड़े आयन (आमतौर पर ऋणायन) सघन पैक संरचना बनाते हैं और छोटे आयन (आमतौर पर धनायन) रिक्त स्थानों में ठहरते हैं। यदि बाद के आयन बहुत छोटे हों तो तेत्रफलकीय रिक्त स्थान भरे जाते हैं, अगर बड़े हों तो अष्टफलकीय रिक्त स्थान भरे जाते हैं। सभी अष्टफलकीय या तेत्रफलकीय रिक्त स्थान भरे नहीं जाते हैं। एक दिए गए यौगिक में, अष्टफलकीय या तेत्रफलकीय रिक्त स्थानों के कितने भाग भरे गए हैं, यौगिक के रासायनिक सूत्र पर निर्भर करता है, जैसा कि निम्नलिखित उदाहरणों से स्पष्ट है।

उदाहरण 1.1

एक यौगिक दो तत्व X और Y से बना है। तत्व Y के परमाणु (ऋणायन के रूप में) ccp जालक बनाते हैं और तत्व X के परमाणु (धनायन के रूप में) सभी अष्टफलक रिक्तियों को घेरते हैं। यौगिक का सूत्र क्या होगा?

हल

Y के तत्व द्वारा ccp जालक बनाया गया है। जालक में उपस्थित Y के परमाणुओं की संख्या के बराबर अष्टफलक रिक्तियों की संख्या होगी। चूंकि सभी अष्टफलक रिक्तियों को X के परमाणुओं द्वारा घेरा गया है, इनकी संख्या Y के परमाणुओं के बराबर होगी। अतः X और Y के परमाणुओं की संख्या समान है या 1:1 के अनुपात में है। अतः यौगिक का सूत्र XY होगा।

उदाहरण 1.2

तत्व B के परमाणु hcp लैटिस बनाते हैं और तत्व A के परमाणु तत्व B के परमाणुओं के तेतरह रिक्त स्थानों के 2/3 भाग पर उपस्थित होते हैं। तत्व $\mathrm{A}$ और $\mathrm{B}$ से बने यौगिक का सूत्र क्या होगा?

हल

तत्व B के परमाणुओं की संख्या के दुगुने तेतरह रिक्त स्थान बनते हैं और इनमें से केवल 2/3 भाग तत्व A के परमाणुओं द्वारा घेरे गए हैं। अतः तत्व A और B के परमाणुओं की संख्या का अनुपात $2 \times (2 / 3): 1$ या $4: 3$ होगा और यौगिक का सूत्र $\mathrm{A_4} \mathrm{~B_3}$ होगा।

तेट्राहेड्रल और ऑक्टाहेड्रल खाली स्थानों के स्थान ज्ञात करना

हम जानते हैं कि सघनतम पैक किए गए संरचनाओं में तेट्राहेड्रल और ऑक्टाहेड्रल खाली स्थान दोनों होते हैं। चलो हम ccp (या fcc) संरचना लें और इसमें इन खाली स्थानों के स्थान ज्ञात करें।

(a) तेट्राहेड्रल खाली स्थानों के स्थान ज्ञात करना

चलो ccp या fcc लैटिस के एक यूनिट सेल को लें [चित्र 1(a)]। यूनिट सेल को आठ छोटे घनों में विभाजित किया गया है।

प्रत्येक छोटे घन में विपरीत कोनों पर परमाणु होते हैं [चित्र 1(a)]। सभी मिलकर, प्रत्येक छोटे घन में 4 परमाणु होते हैं। जब एक दूसरे के साथ जुड़े होते हैं, तो वे एक नियमित चतुष्कोणीय रिक्तियों का निर्माण करते हैं। इसलिए, प्रत्येक छोटे घन में एक चतुष्कोणीय रिक्ति होती है और कुल मिलाकर 8 चतुष्कोणीय रिक्तियाँ होती हैं। प्रत्येक आठ छोटे घन में ccp संरचना के एक यूनिट सेल में एक रिक्ति होती है। हम जानते हैं कि ccp संरचना में प्रत्येक यूनिट सेल में 4 परमाणु होते हैं। इसलिए, चतुष्कोणीय रिक्तियों की संख्या परमाणुओं की संख्या के दोगुनी होती है।

(b) अष्टफलकीय रिक्तियों के स्थान निर्धारण

हम फिर से ccp या fcc लैटिस के एक यूनिट सेल की बात करते हैं [चित्र 2(a)]। घन के शरीर केंद्र, C खाली होता है लेकिन यह चार फलक केंद्र पर छह परमाणुओं द्वारा घिरा होता है। यदि ये फलक केंद्र जुड़े हों, तो एक अष्टफलक बनता है। इसलिए, यह यूनिट सेल में घन के शरीर केंद्र में एक अष्टफलकीय रिक्ति होती है।

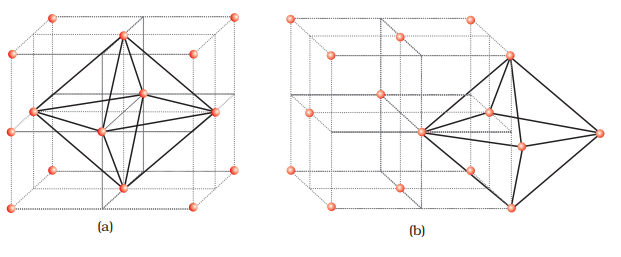
अतिरिक्त शरीर केंद्र के अलावा, प्रत्येक घन के 12 किनारों के केंद्र में एक अष्टफलकीय रिक्त स्थान होता है [चित्र 2(b)]। यह छह अणुओं द्वारा घिरा होता है, जिनमें से चार एक ही एकक कोश के सदस्य होते हैं (2 कोनों पर और 2 फलक केंद्र पर) और दो दो आसन्न एकक कोशों के सदस्य होते हैं। क्योंकि घन के प्रत्येक किनारा चार आसन्न एकक कोशों के बीच साझा होता है, इसलिए अष्टफलकीय रिक्त स्थान भी इस पर स्थित होता है। प्रत्येक रिक्त स्थान के केवल 1/4 भाग एक विशिष्ट एकक कोश के स्वामित्व में होता है।

इस प्रकार घनीय निकटतम पैक की संरचना में: घन के शरीर केंद्र में अष्टफलक रिक्तियाँ = 1 प्रत्येक किनारे पर 12 अष्टफलक रिक्तियाँ और चार एकक कोश के बीच साझा की गई हैं = 12 × 1/4 = 3

कुल अष्टफलक रिक्तियाँ = 4 हम जानते हैं कि ccp संरचना में, प्रत्येक एकक कोश में 4 परमाणु होते हैं। इसलिए, अष्टफलक रिक्तियों की संख्या इस संख्या के बराबर होती है।

1.7 पैक करने की कुशलता

कोई भी तरीके से संघटक कण (परमाणु, अणु या आयन) पैक किए जाएं, कुछ मुक्त जगह हमेशा रिक्तियों के रूप में होती है। पैक करने की कुशलता उस प्रतिशत को दर्शाती है जो कणों द्वारा भरे गए कुल अंतरिक अंश के बराबर होती है। अब हम विभिन्न प्रकार की संरचनाओं में पैक करने की कुशलता की गणना करेंगे।

1.7.1 hcp और ccp संरचनाओं में पैकिंग कुशलता

दोनों प्रकार के सघन पैकिंग (hcp और ccp) समान कुशलता रखते हैं। चलो हम ccp संरचना में पैकिंग की कुशलता की गणना करें। चित्र 1.24 में मान लीजिए एकक कोष्ठक के किनारे की लंबाई ‘a’ है और फेस विकर्ण AC = b है।

In $\triangle \mathrm{ABC}$

$\mathrm{AC}^{2}=\mathrm{b}^{2}=\mathrm{BC}^{2}+\mathrm{AB}^{2}$

$=a^{2}+a^{2}=2 a^{2}$ या

$b=\sqrt{2} a$

यदि $r$ गोले की त्रिज्या है, तो हम ज्ञात करते हैं

$b=4 \mathrm{r}=\sqrt{2} a$

या $a=\frac{4 \mathrm{r}}{\sqrt{2}}=2 \sqrt{2} \mathrm{r}$

(हम इसे भी लिख सकते हैं, $\mathrm{r}=\frac{\mathrm{a}}{2 \sqrt{2}}$ )

हम जानते हैं कि ccp संरचना में प्रत्येक एकक कोष्ठ में 4 गोले के तुल्य अस्तित्व में होते हैं। चार गोलों के कुल आयतन $4 \times(4 / 3) \pi r^{3}$ के बराबर होता है और घन का आयतन $\mathrm{a}^{3}$ या $(2 \sqrt{2} \mathrm{r})^{3}$ होता है।

अतः,

पैकिंग दक्षता $=\frac{\text { एकक कोष्ठ में चार गोलों द्वारा उपलब्ध आयतन } \times 10 बराबर}{\text { एकक कोष्ठ का कुल आयतन }} $%

$$ \begin{aligned} & =\frac{4 \times(4 / 3) \pi r^{3} \times 100}{(2 \sqrt{2} r)^{3}} \% \end{aligned} $$ $$ \begin{aligned} & =\frac{(16 / 3) \pi r^{3} \times 100}{16 \sqrt{2} r^{3}} \% =74 \% \end{aligned} $$

1.7.2 बॉडी सेंट्रेड क्यूबिक संरचनाओं में पैकिंग के दक्षता

चित्र 1.25 से स्पष्ट है कि केंद्र में स्थित परमाणु अन्य दो परमाणुओं से संपर्क में होगा जो विकर्ण व्यवस्था में हैं।

In $\triangle \mathrm{EFD}$,

$\mathrm{b}^{2}=\mathrm{a}^{2}+\mathrm{a}^{2}=2 \mathrm{a}^{2}$

$\mathrm{b}=\sqrt{2} \mathrm{a}$

अब $\triangle$ AFD में

$$ \begin{aligned} & c^{2}=a^{2}+b^{2}=a^{2}+2 a^{2}=3 a^{2} \\ & c=\sqrt{3} a \end{aligned} $$

शरीर के विकर्ण की लंबाई $c$ तीनों गोलियों (परमाणु) के व्यास के बराबर होती है, जो विकर्ण के अनुदिश एक-दूसरे को स्पर्श करती हैं।

इसलिए, $$\quad \sqrt{3} \mathrm{a}=4 \mathrm{r}$$ $$ \mathrm{a}=\frac{4 \mathrm{r}}{\sqrt{3}} $$

$$

हम इस प्रकार लिख सकते हैं, $r=\frac{\sqrt{3}}{4} \mathrm{a}$

इस प्रकार की संरचना में, कुल परमाणुओं की संख्या 2 होती है और उनका आयतन $2 \times\left(\frac{4}{3}\right) \pi \mathrm{r}^{3}$ होता है।

क्यूब का आयतन, $\mathrm{a}^{3}$ बराबर होगा $\left(\frac{4}{\sqrt{3}} \mathrm{r}\right)^{3}$ या $\mathrm{a}^{3}=\left(\frac{4}{\sqrt{3}} \mathrm{r}\right)^{3}$।

इसलिए,

पैकिंग दक्षता $=\frac{\text { इकाई सेल में दो गोलियों द्वारा घेरे गए आयतन } \times 100}{\text { इकाई सेल का कुल आयतन }} \%$

$$ \begin{aligned} & =\frac{2 \times(4 / 3) \pi r^{3} \times 100}{[(4 / \sqrt{3}) r]^{3}} \% \\ & =\frac{(8 / 3) \pi r^{3} \times 100}{64 /(3 \sqrt{3}) r^{3}}=68 \% \end{aligned} $$

1.7.3 सरल घनीय लैटिस में पैकिंग दक्षता

सरल घनीय लैटिस में परमाणु केवल घन के कोनों पर स्थित होते हैं। कण एक भुजा के अनुदिश एक दूसरे को स्पर्श करते हैं (चित्र 1.26)।

इसलिए, घन के किनारे या भुजा की लंबाई ‘a’, और प्रत्येक कण की त्रिज्या, r के बीच संबंध है

$$ \mathrm{a}=2 \mathrm{r} $$

घन एकक कोष्ठ का आयतन $=a^{3}=(2 r)^{3}=8 r^{3}$

एक सरल घन एकक कोष्ठ में केवल 1 परमाणु होता है

उपलब्ध आयतन $=\frac{4}{3} \pi \mathrm{r}^{3}$

पैकिंग दक्षता

$\therefore$ पैकिंग दक्षता $$ \begin{gathered} =\frac{\text { एक परमाणु का आयतन }}{\text { घन एकक कोष्ठ का आयतन }} \times 100 \% \\ =\frac{\frac{4}{3} \pi \mathrm{r}^3}{8 \mathrm{r}^3} \times 100=\frac{\pi}{6} \times 100 \\ $$

=52.36 \%=52.4 \% \end{gathered} $$

इसलिए, हम निष्कर्ष निकाल सकते हैं कि $c c p$ और hcp संरचनाएँ अधिकतम पैकिंग दक्षता के साथ होती हैं।

1.8 इकाई सेल आयामों से संबंधित गणनाएँ

इकाई सेल आयामों से, हम इकाई सेल के आयतन की गणना कर सकते हैं। धातु के घनत्व को जाने पर, हम इकाई सेल में परमाणुओं के द्रव्यमान की गणना कर सकते हैं। एक अकेले परमाणु के द्रव्यमान की निर्धारण एवोगाड्रो स्थिरांक की निर्धारण के एक सटीक विधि प्रदान करता है। मान लीजिए, X-किरण विवर्तन द्वारा निर्धारित एक घनीय क्रिस्टल के इकाई सेल के किनारे की लंबाई a है, d ठोस पदार्थ का घनत्व और M मोलर द्रव्यमान है। घनीय क्रिस्टल के मामले में:

कायून कोष्ठ का आयतन $=a^{3}$

कायून कोष्ठ के द्रव्यमान

$=$ कोष्ठ में परमाणुओं की संख्या $\times$ प्रत्येक परमाणु का द्रव्यमान $=Z \times m$

(यहाँ $z$ एक कायून कोष्ठ में उपस्थित परमाणुओं की संख्या है और $m$ एक परमाणु का द्रव्यमान है)

कायून कोष्ठ में उपस्थित परमाणु का द्रव्यमान:

$$ m=\frac{M}{N_{A}}(M \text { अपेक्षित द्रव्यमान है }) $$

इसलिए, कायून कोष्ठ का घनत्व

$$ \begin{aligned} & =\frac{\text { कायून कोष्ठ का द्रव्यमान }}{\text { कायून कोष्ठ का आयतन }} \\ & =\frac{z \cdot m}{a^{3}}=\frac{z \cdot M}{a^{3} \cdot N_{A}} \text { या } d=\frac{z M}{a^{3} N_{A}} $$

\end{aligned} $$

याद रखें, इकाई कोश के घनत्व को वस्तु के घनत्व के बराबर माना जाता है। ठोस के घनत्व को हमेसा अन्य विधियों द्वारा निर्धारित किया जा सकता है। पांच पैरामीटर $\left(d, z M, a\right.$ और $\left.N_{A}\right)$ में से चार ज्ञात होने पर, हम पांचवीं को निर्धारित कर सकते हैं।

उदाहरण 1.3

एक तत्व के एक बॉडी सेंट्रेड क्यूबिक (bcc) संरचना है जिसकी कोश किन्हर की लंबाई $288 \mathrm{pm}$ है। तत्व का घनत्व $7.2 \mathrm{~g} / \mathrm{cm}^{3}$ है। तत्व के $208 \mathrm{~g}$ में कितने परमाणु उपस्थित हैं?

हल

इकाई सेल का आयतन $=(288 \mathrm{pm})^{3}$

$$ \begin{aligned} & =\left(288 \times 10^{-12} \mathrm{~m}\right)^{3}=\left(288 \times 10^{-10} \mathrm{~cm}\right)^{3} \\ & =2.39 \times 10^{-23} \mathrm{~cm}^{3} \end{aligned} $$

तत्व के $208 \mathrm{~g}$ का आयतन

$$ =\frac{\text { द्रव्यमान }}{\text { घनत्व }}=\frac{208 \mathrm{~g}}{7.2 \mathrm{~g} \mathrm{~cm}^{-3}}=28.88 \mathrm{~cm}^{3} $$

इस आयतन में इकाई सेल की संख्या

$$ =\frac{28.88 \mathrm{~cm}^{3}}{2.39 \times 10^{-23} \mathrm{~cm}^{3} / \text { unit cell }}=12.08 \times 10^{23} \text { unit cells } $$

$$

क्योंकि प्रत्येक $b c c$ घन एकक कोष्ठ में 2 परमाणु होते हैं, इसलिए $208 \mathrm{~g}=2$ (परमाणु/एकक कोष्ठ) $\times 12.08 \times 10^{23}$ एकक कोष्ठ

$$ =24.16 \times 10^{23} \text { परमाणु } $$

उदाहरण 1.4

एक्स-रे विवर्तन अध्ययन यह दर्शाते हैं कि तांबा एक fcc एकक कोष्ठ में जमा होता है जिसकी कोष्ठ किनारा 3.608×10-8 सेमी है। एक अलग प्रयोग में, तांबा के घनत्व को 8.92 ग्राम/सेमी³ निर्धारित किया गया है, तांबा के परमाणु द्रव्यमान की गणना करें।

fcc जालक के मामले में, एकक कोष्ठ में परमाणुओं की संख्या, z = 4 परमाणु

इसलिए, $M=\frac{\mathrm{dN}_{\mathrm{A}} \mathrm{a}^{3}}{\mathrm{Z}}$

$=63.1 \mathrm{~g} / \mathrm{mol}$

ताम्बू के परमाणु द्रव्यमान $=63.1 \mathrm{u}$

उदाहरण 1.5

चांदी ccp लेटिस में बनती है और इसके क्रिस्टल के X-किरण अध्ययन दिखाते हैं कि इसके यूनिट सेल के किनारे की लंबाई 408.6 पिकोमीटर है। चांदी का घनत्व गणना कीजिए (परमाणु द्रव्यमान = 107.9 u)।

क्योंकि लेटिस ccp है, तो इकाई सेल में चांदी के परमाणुओं की संख्या = z = 4 चांदी का मोलर द्रव्यमान $=107.9 \mathrm{~g} \mathrm{~mol}^{-1}=107.9 \times 10^{-3} \mathrm{~kg} \mathrm{~mol}^{-1}$

कोष्ठक के किनारे की लंबाई $=\mathrm{a}=408.6 \mathrm{pm}=408.6 \times 10^{-12} \mathrm{~m}$

घनत्व, $d=\frac{z \cdot \mathrm{M}}{\mathrm{a}^{3} \cdot \mathrm{N}_{\mathrm{A}}}$

$$ \begin{aligned} & =\frac{4 \times\left(107.9 \times 10^{-3} \mathrm{~kg} \mathrm{~mol}^{-1}\right)}{\left(408.6 \times 10^{-12} \mathrm{~m}\right)^{3}\left(6.022 \times 10^{23} \mathrm{~mol}^{-1}\right)}=10.5 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3} \\ & =10.5 \mathrm{~g} \mathrm{~cm}^{-3} \end{aligned} $$

अंतर्गत प्रश्न

1.13 वर्गीय संपीड़ित संरचना में एक अणु के द्वि-विमीय समन्वय संख्या क्या होती है?

उत्तर दिखाएं

उत्तर

वर्गीय संपीड़ित संरचना में, एक अणु अपने चारों ओर चार पड़ोसियों के संपर्क में होता है। अतः वर्गीय संपीड़ित संरचना में एक अणु के द्वि-विमीय समन्वय संख्या 4 होती है।

1.14 एक यौगिक षष्ठांशीय संपीड़ित संरचना बनाता है। इसके 0.5 मोल में कुल रिक्तियों की संख्या क्या होती है? इनमें से कितनी त्रिकोणी रिक्तियाँ होती हैं?

उत्तर दिखाएं

उत्तर

संपीड़ित कणों की संख्या $=0.5 \times 6.022 \times 10^{23}=3.011 \times 10^{23}$

अतः, अष्टफलक रिक्तियों की संख्या $=3.011 \times 10^{23}$

और, त्रिकोणी रिक्तियों की संख्या $=2 \times 3.011 \times 10^{23}=6.022 \times 10^{23}$

अतः, कुल रिक्तियों की संख्या $=3.011 \times 10^{23}+6.022 \times 10^{23}=9.033 \times 10^{23}$

1.15 एक यौगिक दो तत्व $M$ और $N$ से बना है। तत्व $N$ $ccp$ बनाता है और $M$ के अणु $N$ के त्रिकोणी रिक्तियों के $1/3^{\text {rd }}$ भाग पर बसते हैं। यौगिक का सूत्र क्या होता है?

उत्तर दिखाएं

उत्तर

तत्व $N$ के अणुओं द्वारा $ccp$ जालक बनाया गया है।

यहाँ, उत्पन्न त्रिकोणी रिक्तियों की संख्या तत्व $N$ के अणुओं की संख्या के दोगुनी होती है।

प्रश्न के अनुसार, तत्व $M$ के अणु $N$ के त्रिकोणी रिक्तियों के $1/3^{\text {rd }}$ भाग पर बसते हैं।

अतः, $M$ के अणुओं की संख्या $N$ के अणुओं की संख्या के $2/3$ भाग के बराबर होती है।

अतः, $M$ और $N$ के अणुओं की संख्या के अनुपात $M: N = \frac{2}{3}: 1$ $=2: 3$

इसलिए, यौगिक का सूत्र $\mathrm{M_2} \mathrm{~N_3}$ होता है।

1.16 निम्नलिखित में से कौन सा जालक सबसे अधिक भरे हुए होता है (i) सरल घनीय (ii) बॉडी सेंट्रल घनीय और (iii) षष्ठांशीय संपीड़ित जालक?

उत्तर दिखाएँ

उत्तर

हेक्सागोनल क्लोज़ पैक्ड लैटिस की पैकिंग दक्षता $74 \%$ होती है। सरल घनीय और बॉडी सेंट्रेड घनीय लैटिस की पैकिंग दक्षता क्रमशः $52.4 \%$ और $68 \%$ होती है।

1.17 एक तत्व जिसका मोलर द्रव्यमान $2.7 \times 10^{-2} \mathrm{~kg} \mathrm{~mol}^{-1}$ है, एक घन एकक कोश के रूप में बनाता है जिसकी किनारा लंबाई $405 \mathrm{pm}$ है। यदि इसका घनत्व $2.7 \times 103 \mathrm{~kg} \mathrm{~m}^{-3}$ है, तो घन एकक की प्रकृति क्या है?

उत्तर दिखाएँ

उत्तर

दिया गया है कि तत्व का घनत्व, $d=2.7 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$

मोलर द्रव्यमान, $\mathrm{M}=2.7 \times 10^{-2} \mathrm{~kg} \mathrm{~mol}^{-1}$

किनारा लंबाई, $a=405 \mathrm{pm}=405 \times 10^{-12} \mathrm{~m}$

$=4.05 \times 10^{-10} \mathrm{~m}$

ज्ञात है कि, आवोगाड्रो संख्या, $N_{A}=6.022 \times 1023 \mathrm{~mol}^{-1}$

संबंध के उपयोग द्वारा,

$$ \begin{aligned} d & =\frac{z, M}{a^{3} \cdot \mathrm{N_A}} \\ \end{aligned} $$

$$ \begin{aligned} z & =\frac{d \cdot a^{3} \mathrm{~N_A}}{M} \\ & =\frac{2.7 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3} \times\left(4.05 \times 10^{-10} \mathrm{~m}\right)^{3} \times 6.022 \times 10^{23} \mathrm{~mol}^{-1}}{2.7 \times 10^{-2} \mathrm{~kg} \mathrm{~mol}^{-1}} \\ & =4.004 \\ & =4 \end{aligned} $$

इससे यह स्पष्ट होता है कि एकक कोश में तत्व के चार परमाणु उपस्थित हैं। अतः, एकक कोश फेस सेंट्रेड घनीय (fcc) या घनीय क्लोज़ पैक्ड ( $c c p$ ) है।

1.9 ठोसों में त्रुटियाँ

हालांकि क्रिस्टलीय ठोसों में अपने संघटक कणों के व्यवस्था में छोटी दूरी और लंबी दूरी के क्रम दोनों होते हैं, लेकिन क्रिस्टल पूर्ण नहीं होते हैं। आमतौर पर एक ठोस अपने संघटक कणों के एक बड़ी संख्या के छोटे क्रिस्टलों के समूह से बना होता है। इन छोटे क्रिस्टलों में त्रुटियाँ होती हैं। यह घटना क्रिस्टलीकरण प्रक्रिया तेज या मध्यम दर पर होने पर होती है। जब क्रिस्टलीकरण प्रक्रिया बहुत धीमी दर पर होती है तो एकल क्रिस्टल बनते हैं। यहाँ तक कि इन क्रिस्टलों में भी त्रुटियाँ नहीं रहती हैं। त्रुटियाँ मूल रूप से अपने संघटक कणों के व्यवस्था में अनियमितता होती है। बड़े अर्थ में, त्रुटियाँ दो प्रकार की होती हैं, जैसे कि बिंदु त्रुटियाँ और रेखा त्रुटियाँ। बिंदु त्रुटियाँ क्रिस्टलीय पदार्थ में एक बिंदु या एक परमाणु के आसपास आदर्श व्यवस्था से विचलन या अनियमितता होती है, जबकि रेखा त्रुटियाँ एक पूरी लेटिस पॉइंट की पंक्ति में आदर्श व्यवस्था से विचलन या अनियमितता होती है। इन अनियमितताओं को क्रिस्टल त्रुटियाँ कहते हैं। हम अपने विवेचन को केवल बिंदु त्रुटियों तक सीमित रखेंगे।

1.9.1 बिंदु दोष के प्रकार

बिंदु दोष को तीन प्रकारों में वर्गीकृत किया जा सकता है : (i) स्टोइकियोमेट्रिक दोष (ii) अशुद्धि दोष और (iii) अस्टोइकियोमेट्रिक दोष।

(a) स्टोइकियोमेट्रिक दोष ये बिंदु दोष हैं जो ठोस के स्टोइकियोमेट्री को बिगाड़ते नहीं हैं। इन्हें आंतरिक या थर्मोडायनामिक दोष के रूप में भी कहा जाता है। मूल रूप से ये दो प्रकार के होते हैं, खाली दोष और अंतराल दोष।

(i) खाली स्थान दोष: जब क्रिस्टल के कुछ लेटिस साइट खाली हो जाते हैं, तो क्रिस्टल को खाली स्थान दोष कहा जाता है (चित्र 1.27)। इस दोष के कारण पदार्थ के घनत्व में कमी हो जाती है। इस दोष का विकास जब भी पदार्थ को गरम किया जाता है, हो सकता है।

(ii) अंतराल दोष: जब कुछ संघटक कण (परमाणु या अणु) अंतराल साइट पर बैठ जाते हैं, तो क्रिस्टल को अंतराल दोष कहा जाता है (चित्र 1.28)। इस दोष के कारण पदार्थ के घनत्व में वृद्धि होती है।

ऊपर वर्णित खाली स्थान और अंतराल दोष अन-आयनिक ठोसों द्वारा दिखाए जा सकते हैं। आयनिक ठोस हमेशा विद्युत उदासीनता के बराबर रहते हैं। इनके साथ खाली स्थान या अंतराल दोष के बजाए वे फ्रेंकल और शॉट्की दोष दिखाते हैं।

(iii) फ्रेंकल दोष: यह दोष आयनिक ठोस द्वारा प्रदर्शित किया जाता है। छोटा आयन (आमतौर पर धनायन) अपने सामान्य स्थान से एक अंतरालीय स्थान पर विस्थापित हो जाता है (चित्र 1.29)। इसके प्रारंभिक स्थान पर एक रिक्ति दोष और नए स्थान पर एक अंतरालीय दोष उत्पन्न हो जाता है।

फ्रेंकल दोष को अपस्थापन दोष के रूप में भी जाना जाता है। यह ठोस के घनत्व को बदलता नहीं है। फ्रेंकल दोष उन आयनिक पदार्थों में प्रदर्शित होता है जहाँ आयनों के आकार में बहुत अधिक अंतर होता है, उदाहरण के लिए, $\mathrm{ZnS}, \mathrm{AgCl}, \mathrm{AgBr}$ और $\mathrm{AgI}$ के कारण $\mathrm{Zn}^{2+}$ और $\mathrm{Ag}^{+}$ आयनों के छोटे आकार के कारण।

(iv) शॉट्स्की दोष: यह मूल रूप से आयनिक ठोसों में एक रिक्तिका दोष है। विद्युत उदासीनता के बरकरार रखने के लिए, अपाचे धनायन और नकारात्मक आयनों की संख्या बराबर होती है (चित्र 1.30)।

सरल रिक्ति दोष के जैसे, शॉट्टकी दोष भी पदार्थ के घनत्व को कम करता है। आयनिक ठोस में ऐसे दोषों की संख्या बहुत अधिक होती है। उदाहरण के लिए, कमरे के तापमान पर $\mathrm{NaCl}$ में लगभग $10^{6}$ शॉट्टकी युग्म प्रति $\mathrm{cm}^{3}$ होते हैं। $1 \mathrm{~cm}^{3}$ में लगभग $10^{22}$ आयन होते हैं। अतः, $10^{16}$ आयनों में एक शॉट्टकी दोष होता है। शॉट्टकी दोष उन आयनिक पदार्थों में दिखाई देता है जिनमें धनायन और ऋणायन के आकार लगभग समान होते हैं। उदाहरण के लिए, $\mathrm{NaCl}, \mathrm{KCl}, \mathrm{CsCl}$ और $\mathrm{AgBr}$। ध्यान देने योग्य है कि AgBr दोनों, फ्रेंगल दोष और शॉट्टकी दोष दिखाई देता है।

(ब) अशुद्धि अपसारण : यदि थोड़ी मात्रा में $\mathrm{SrCl_2}$ वाला $\mathrm{NaCl}$ का द्रव शुद्ध करके ठंढा हो जाता है, तो कुछ $\mathrm{Na}^{+}$ आयनों के स्थान पर $\mathrm{Sr}^{2+}$ आयन बैठ जाते हैं। प्रत्येक $\mathrm{Sr}^{2+}$ आयन दो $\mathrm{Na}^{+}$ आयनों के स्थान ले लेता है। यह एक आयन के स्थान पर बैठ जाता है और दूसरा स्थान खाली रह जाता है। इस प्रकार उत्पन्न धनायन खाली स्थान बराबर $\mathrm{Sr}^{2+}$ आयनों की संख्या के बराबर होते हैं। एक अन्य समान उदाहरण $\mathrm{CdCl}_{2}$ और $\mathrm{AgCl}$ के ठोस समाधान है।

(c) अस्थिर अनुपाती दोष : इस तक चर्चा किए गए दोष अवस्थित ठोस के अनुपात को बिगाड़ते नहीं हैं। हालांकि, अनेक अस्थिर अनुपाती अकार्बनिक ठोस जाने जाते हैं जो अपने क्रिस्टल संरचना में दोष के कारण अपने संघटक तत्वों के अस्थिर अनुपात में विद्यमान होते हैं। इन दोषों के दो प्रकार होते हैं: (i) धातु अधिकता दोष और (ii) धातु कमी दोष।

(i) धातु अधिकता दोष : एक ऋणायन रिक्तियों के कारण धातु अधिकता दोष: NaCl और KCl जैसे अल्कली हैलाइड इस प्रकार के दोष को प्रदर्शित करते हैं। जब NaCl के क्रिस्टल को सोडियम वाष्प के वातावरण में गरम किया जाता है, तो सोडियम परमाणु क्रिस्टल के सतह पर जमा हो जाते हैं। Cl⁻ आयन क्रिस्टल के सतह तक पहुंचकर सोडियम परमाणुओं के साथ संयोग करके NaCl बनाते हैं। यह घटना सोडियम परमाणुओं के द्वारा इलेक्ट्रॉन के नुकसान के कारण होती है जिससे Na⁺ आयन बनते हैं। निकाले गए इलेक्ट्रॉन क्रिस्टल में चले जाते हैं और ऋणायन साइटों पर बैठ जाते हैं (चित्र 1.32)। इसके परिणामस्वरूप क्रिस्टल में सोडिजम की अधिकता हो जाती है। अनुपाती साइटों पर बैठे अकुंजित इलेक्ट्रॉन फ़-सेंटर (जर्मन शब्द Farbenzenter के लिए रंग केंद्र) कहलाते हैं। ये NaCl के क्रिस्टल को पीला रंग देते हैं। रंग उत्पन्न होता है जब इन इलेक्ट्रॉनों को क्रिस्टल पर पड़ने वाले प्रकाश की ऊर्जा के अवशोषण के कारण उत्तेजित होते हैं। इसी तरह, लिथियम की अधिकता LiCl क्रिस्टल को लाल रंग देती है और पोटेशियम की अधिकता KCl क्रिस्टल को बैगनी (या लिली) रंग देती है।

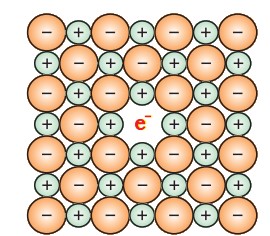
à अतिरिक्त धातु अपस्थिति अंतराकाशी स्थलों पर अतिरिक्त धनायनों की उपस्थिति के कारण: जिंक ऑक्साइड कमरे के तापमान पर सफेद रंग का होता है। गरम करने पर यह ऑक्सीजन खो देता है और पीला हो जाता है। $$ \mathrm{ZnO} \xrightarrow{\text { heating }} \mathrm{Zn}^{2+}+\frac{1}{2} \mathrm{O_2}+2 \mathrm{e}^{-} $$

अब क्रिस्टल में जिंक की अतिरिक्त मात्रा हो जाती है और इसका सूत्र $\mathrm{Zn_1+\mathrm{x}} \mathrm{O}$ बन जाता है। अतिरिक्त $\mathrm{Zn}^{2+}$ आयन अंतराकाशी स्थलों पर चले जाते हैं और इलेक्ट्रॉन आसपास के अंतराकाशी स्थलों पर चले जाते हैं।

(ii) धातु कमी दोष कई ठोस पदार्थ आवृत्ति अनुपात में तैयार करना कठिन होता है और धातु की मात्रा आवृत्ति अनुपात की तुलना में कम होती है। इस प्रकार के एक सामान्य उदाहरण है $\mathrm{FeO}$ जो अधिकांशतः $\mathrm{Fe_0.95} \mathrm{O}$ संरचना में पाया जाता है। यह वास्तव में $\mathrm{Fe_0.93} \mathrm{O}$ से $\mathrm{Fe_0.96} \mathrm{O}$ तक बदल सकता है। $\mathrm{FeO}$ के क्रिस्टल में कुछ $\mathrm{Fe}^{2+}$ आयन अनुपस्थित होते हैं और धनात्मक आवेश की कमी को आवश्यक संख्या में $\mathrm{Fe}^{3+}$ आयनों की उपस्थिति द्वारा भरा जाता है।

1.10 विद्युत गुण

ठोस पदार्थ विद्युत चालकता के अद्भुत रूप से विस्तारित श्रेणी में होते हैं, जो $10^{-20}$ से $10^{7} \mathrm{ohm}^{-1} \mathrm{~m}^{-1}$ तक फैली होती है। ठोस को उनकी चालकता के आधार पर तीन प्रकारों में वर्गीकृत किया जा सकता है।

(i) चालक: वे ठोस जिनकी चालकता $10^{4}$ से $10^{7} \mathrm{ohm}^{-1} \mathrm{~m}^{-1}$ के बीच होती है, चालक कहलाते हैं। धातुओं की चालकता $10^{7} \mathrm{oh,}^{-1} \mathrm{~m}^{-1}$ के क्रम में होती है और वे अच्छे चालक होते हैं।

(ii) आइसोलेटर : ये ऐसे ठोस होते हैं जिनकी बहुत कम चालकता होती है जो $10^{-20}$ से $10^{-10} \mathrm{ohm}^{-1} \mathrm{~m}^{-1}$ के बीच होती है।

(iii) अर्धचालक : ये ऐसे ठोस होते हैं जिनकी चालकता $10^{-6}$ से $10^{4} \mathrm{ohm}^{-1} \mathrm{~m}^{-1}$ के बीच के मध्यवर्ती रेंज में होती है।

चालकता इन अंतर्निहित चालकों के लिए बहुत कम होती है ताकि वे व्यावहारिक उपयोग के लिए उपयोगी नहीं हो सकते। इनकी चालकता उपयुक्त अशुद्धि के उचित मात्रा में जोड़कर बढ़ाई जा सकती है। इस प्रक्रिया को डोपिंग कहते हैं। डोपिंग एक अशुद्धि के साथ किया जा सकता है जो अंतर्निहित चालक बर्तन जैसे सिलिकॉन या जर्मेनियम की तुलना में इलेक्ट्रॉन समृद्ध या इलेक्ट्रॉन अभाव वाली हो सकती है। ऐसी अशुद्धियाँ उनमें इलेक्ट्रॉनिक त्रुटियों को प्रोत्साहित करती हैं।

(a) इलेक्ट्रॉन समृद्ध अशुद्धियाँ सिलिकॉन और जर्मेनियम आवर्त सारणी के समूह 14 में स्थित होते हैं और प्रत्येक के चार संयोजक इलेक्ट्रॉन होते हैं। उनके क्रिस्टल में प्रत्येक परमाणु अपने पड़ोसियों के साथ चार सहसंयोजक बंधन बनाता है (चित्र 1.34 a)। जब इन्हें समूह 15 के तत्व जैसे P या As जिनमें पांच संयोजक इलेक्ट्रॉन होते हैं, के साथ डोप किया जाता है, तो वे सिलिकॉन या जर्मेनियम के क्रिस्टल के कुछ लेटिस साइट पर बैठ जाते हैं (चित्र 1.34 b)। पांच इलेक्ट्रॉन में से चार चार सहसंयोजक बंधन बनाने में उपयोग किए जाते हैं जो चार पड़ोसी सिलिकॉन परमाणुओं के साथ होते हैं। पांचवां इलेक्ट्रॉन अतिरिक्त हो जाता है और विस्थापित हो जाता है। इन विस्थापित इलेक्ट्रॉनों के कारण डोप किए गए सिलिकॉन (या जर्मेनियम) की चालकता बढ़ जाती है। यहाँ चालकता के बढ़ने का कारण ऋणावेशित इलेक्ट्रॉन के कारण है, इसलिए इलेक्ट्रॉन समृद्ध अशुद्धि के साथ डोप किए गए सिलिकॉन को n-टाइप चालक कहते हैं।

(b) इलेक्ट्रॉन - अभाव अशुद्धियाँ सिलिकॉन या जर्मेनियम को B, Al या Ga जैसे समूह 13 के तत्व भी डॉपिंग करके बनाया जा सकता है जो केवल तीन बाह्य इलेक्ट्रॉन रखते हैं। जहाँ चौथा बाह्य इलेक्ट्रॉन अनुपस्थित होता है, वहाँ इलेक्ट्रॉन छेद या इलेक्ट्रॉन अभाव कहलाता है (चित्र 1.34 c)। एक इलेक्ट्रॉन आसपास के परमाणु से आकर इलेक्ट्रॉन छेद को भर सकता है, लेकिन इस प्रक्रिया में इसके मूल स्थान पर एक इलेक्ट्रॉन छेद बन जाता है। यदि ऐसा होता है, तो यह लगे जैसे कि इलेक्ट्रॉन छेद इलेक्ट्रॉन द्वारा भरे गए दिशा के विपरीत दिशा में गति कर रहा हो। विद्युत क्षेत्र के प्रभाव में, इलेक्ट्रॉन धनात्मक आवेशित प्लेट की ओर इलेक्ट्रॉन छेद के माध्यम से गति करते हैं, लेकिन यह लगे जैसे कि इलेक्ट्रॉन छेद धनात्मक आवेशित हो रहे हों और ऋणात्मक आवेशित प्लेट की ओर गति कर रहे हों। इस प्रकार के अर्धचालकों को p-प्रकार अर्धचालक कहा जाता है।

n-प्रकार और p-प्रकार अधिकारी चालक के अनुप्रयोग

n-प्रकार और p-प्रकार अऊधिकारी चालक के विभिन्न संयोजन इलेक्ट्रॉनिक घटकों के निर्माण के लिए उपयोग किए जाते हैं। डायोड एक n-प्रकार और p-प्रकार अऊधिकारी चालक के संयोजन होता है और एक डायोड के रूप में उपयोग किया जाता है। ट्रांजिस्टर दो अलग-अलग प्रकार के अऊधिकारी चालक के बीच एक एकल प्रकार के अऊधिरारी चालक के एक लेयर के संयोजन से बनाए जाते हैं। npn और pnp प्रकार के ट्रांजिस्टर रेडियो या ऑडियो संकेतों का पता लगाने या आवर्धन के लिए उपयोग किए जाते हैं। सौर सेल एक प्रभावशाली फोटो डायोड है जो प्रकाश ऊर्जा को विद्युत ऊर्जा में परिवर्तित करने के लिए उपयोग किया जाता है।

जर्मेनियम और सिलिकॉन समूह 14 के तत्व हैं और इसलिए, उनका वर्णनात्मक मूल्य चार होता है और डायमंड के समान चार बंधन बनाते हैं। समूह 13 और 15 या 12 और 16 के संयोजन द्वारा एक बड़ी विविधता के ठोस अवस्था वाले अवस्था तैयार किए गए हैं जो जर्मेनियम या सिलिकॉन के समान औसत मूल्य के समान होते हैं। समूह $13-15$ के सामान्य यौगिक InSb, AlP और GaAs हैं। गैलियम आर्सेनाइट (GaAs) अर्धचालक बहुत तेज जवाब देते हैं और अर्धचालक उपकरणों के डिज़ाइन में क्रांति लाए हैं। ZnS, CdS, CdSe और HgTe $12-16$ समूह के यौगिकों के उदाहरण हैं। इन यौगिकों में बंधन पूरी तरह से सहसंयोजक नहीं होते हैं और आयनिक गुण दो तत्वों के विद्युत ऋणात्मकता पर निर्भर करता है।

हर वस्तु के कुछ चुंबकीय गुण होते हैं। इन गुणों की उत्पत्ति इलेक्ट्रॉन में होती है। परमाणु में प्रत्येक इलेक्ट्रॉन एक छोटे से चुंबक के रूप में व्यवहार करता है। इसका चुंबकीय आघूर्ण दो प्रकार के गतियों से उत्पन्न होता है (i) नाभिक के चारों ओर इलेक्ट्रॉन का कक्षीय गति और (ii) इलेक्ट्रॉन के अपने अक्ष के चारों ओर घूमना (चित्र 1.35)। इलेक्ट्रॉन एक चार्जित कण होता है और इन गतियों के कारण इसे एक छोटे से विद्युत धारा के लूप के रूप में विचार किया जा सकता है जो चुंबकीय आघूर्ण के साथ युक्त होता है। इस प्रकार, प्रत्येक इलेक्ट्रॉन के साथ एक स्थायी चुंबकीय आघूर्ण और एक कक्षीय चुंबकीय आघूर्ण संबंधित होता है। इस चुंबकीय आघूर्ण के मान बहुत छोटा होता है और इसे बोहर चुंबकीय आघूर्ण, μB के इकाई में मापा जाता है। यह 9.27 × 10–24A m2 के बराबर होता है।

उनके चुंबकीय गुणों के आधार पर, पदार्थों को पांच श्रेणियों में वर्गीकृत किया जा सकता है: (i) पैरामैग्नेटिक (ii) डायमैग्नेटिक (iii) फेरोमैग्नेटिक (iv) एंटीफेरोमैग्नेटिक और (v) फेरिमैग्नेटिक।

(i) पैरामैग्नेटिकता: पैरामैग्नेटिक पदार्थ एक चुंबकीय क्षेत्र के द्वारा कमजोर रूप से आकर्षित होते हैं। वे एक चुंबकीय क्षेत्र में चुंबकीय क्षेत्र की दिशा के समान चुंबकीय बनते हैं। चुंबकीय क्षेत्र के अनुपस्थिति में वे अपनी चुंबकता खो बर्बाद कर देते हैं। पैरामैग्नेटिकता एक या एक से अधिक असंगत इलेक्ट्रॉनों की उपस्थिति के कारण होती है जो चुंबकीय क्षेत्र द्वारा आकर्षित होते हैं। $\mathrm{O_2}, \mathrm{Cu}^{2+}, \mathrm{Fe}^{3+}, \mathrm{Cr}^{3+}$ इस प्रकार के पदार्थों के कुछ उदाहरण हैं।

(ii) विद्युत चुम्बकत्व: विद्युत चुम्बकीय पदार्थ चुम्बकीय क्षेत्र द्वारा कमजोर रूप से विकर्षित होते हैं। $\mathrm{H_2} \mathrm{O}, \mathrm{NaCl}$ और $\mathrm{C_6} \mathrm{H_6}$ इस प्रकार के पदार्थों के कुछ उदाहरण हैं। एक चुम्बकीय क्षेत्र में वे कमजोर रूप से चुम्बकीय रूप से चुम्बकीय क्षेत्र के विपरीत दिशा में चुम्बकीय रूप से चुम जाते हैं। विद्युत चुम्बकत्व वे पदार्थ दिखाते हैं जिनमें सभी इलेक्ट्रॉन युग्मित होते हैं और कोई अयुग्मित इलेक्ट्रॉन नहीं होते। इलेक्ट्रॉन के युग्मन उनके चुम्बकीय आघूर्ण को रद्द कर देता है और वे अपने चुम्बकीय गुण खो बैठते हैं।

(iii) लोहचुम्बकत्व: कुछ पदार्थ जैसे लोहा, कोबाल्ट, निकल, गैडोलिनियम और CrO2 एक चुम्बकीय क्षेत्र द्वारा बहुत मजबूत रूप से आकर्षित होते हैं। ऐसे पदार्थों को लोहचुम्बकीय पदार्थ कहा जाता है। इन पदार्थों के अलावा मजबूत आकर्षण के अतिरिक्त, ये पदार्थ अनंतकालीन रूप से चुम्बकीय रूप से चुम्बकीय बन सकते हैं। ठोस अवस्था में, लोहचुम्बकीय पदार्थ के धातु आयन छोटे क्षेत्रों में व्यवस्थित हो जाते हैं जिन्हें डोमेन कहा जाता है। इस प्रकार, प्रत्येक डोमेन एक छोटे से चुम्बक के रूप में कार्य करता है। एक अचुम्बकीय लोहचुम्बकीय पदार्थ के टुकड़े में डोमेन यादृच्छिक रूप से व्यवस्थित होते हैं और उनके चुम्बकीय आघूर्ण रद्द हो जाते हैं। जब पदार्थ को एक चुम्बकीय क्षेत्र में रखा जाता है, तो सभी डोमेन चुम्बकीय क्षेत्र की दिशा में व्यवस्थित हो जाते हैं (चित्र 1.36 a) और एक मजबूत चुम्बकीय प्रभाव उत्पन्न होता है। इस डोमेन की व्यवस्था चुम्बकीय क्षेत्र के हटाए जाने के बाद भी बनी रहती है और लोहचुम्बकीय पदार्थ एक अनंतकालीन चुम्बक बन जाता है।

(iv) अन्तरालोक चुंबकत्व: MnO जैसी वस्तुएं जो अन्तरालोक चुंबकत्व प्रदर्शित करती हैं, लौह चुंबकीय वस्तुओं के समान क्षेत्र संरचना रखती हैं, लेकिन उनके क्षेत्र विपरीत दिशाओं में व्यवस्थित होते हैं और एक दूसरे के चुंबकीय आघूर्ण को विपरीत कर देते हैं (चित्र 1.36 b)।

(v) फेर्रिमैग्नेटिज़म: जब वस्तु के क्षेत्रों में चुंबकीय आघूर्ण समान आकार में समान और विपरीत दिशाओं में व्यवस्थित होते हैं, तो फेर्रिमैग्नेटिज़म प्रेक्षित होता है (चित्र $1.32 \mathrm{c}$)। ये वस्तुएं लौह चुं बकीय वस्तुओं की तुलना में कम आकर्षित होती हैं। $\mathrm{Fe_3} \mathrm{O_4}$ (मैग्नेटाइट) और फेराइट जैसे $\mathrm{MgFe_2} \mathrm{O_4}$ और $\mathrm{ZnFe_2} \mathrm{O_4}$ इस प्रकार की वस्तुओं के उदाहरण हैं। ये वस्तुएं गरम करने पर फेर्रिमैग्नेटिज़म खो बर्बाद हो जाती हैं और पैरामैग्नेटिक बन जाती हैं।

अंतर्गत प्रश्न

1.18 जब एक ठोस को गर्म किया जाता है तो कौन सा दोष उत्पन्न हो सकता है? इसके किस भौतिक गुण पर प्रभाव पड़ता है और किस तरह?

उत्तर दिखाएं

उत्तर

जब एक ठोस को गर्म किया जाता है तो खाली स्थल (vacancy) दोष उत्पन्न हो सकता है। जब कुछ लेटिस साइट खाली हो जाते हैं तो एक ठोस क्रिस्टल को खाली स्थल दोष कहा जाता है।

खाली स्थल दोष ठोस के घनत्व के घटने के कारण होता है।

1.19 निम्नलिखित में से कौन सा स्टोइकियोमेट्रिक दोष दिखाता है: (i) ZnS (ii) AgBr

उत्तर दिखाएं

उत्तर

(i) ZnS Frenkel दोष दिखाता है।

(ii) AgBr भी Frenkel दोष दिखाता है तथा Schottky दोष भी दिखाता है।

1.20 जब एक उच्च आवेश वाला धनायन एक आयनिक ठोस में अशुद्धि के रूप में जोड़ा जाता है तो खाली स्थल कैसे उत्पन्न होते हैं?

उत्तर दिखाएं

उत्तर

जब एक उच्च आवेश वाला धनायन एक आयनिक ठोस में अशुद्धि के रूप में जोड़ा जाता है तो यह उच्च आवेश वाला धनायन कम आवेश वाले धनायन के स्थान पर एक से अधिक धनायन के स्थान पर बैठ जाता है ताकि क्रिस्टल विद्युत उदासीन रहे। इस प्रक्रिया में कुछ साइट खाली हो जाती हैं। उदाहरण के लिए, जब $\mathrm{Sr}^{2+}$ को $\mathrm{NaCl}$ में जोड़ा जाता है, तो प्रत्येक $\mathrm{Sr}^{2+}$ आयन दो $\mathrm{Na}^{+}$ आयनों के स्थान पर बैठ जाता है। हालांकि, एक $\mathrm{Sr}^{2+}$ आयन एक $\mathrm{Na}^{+}$ आयन के स्थान पर बैठ जाता है और दूसरी साइट खाली रह जाती है। इसलिए, खाली स्थल उत्पन्न हो जाते हैं।

1.21 धातु अधिकता दोष के कारण ऋणायन रिक्तियों के कारण आयनिक ठोस रंग ले लेते हैं। एक उपयुक्त उदाहरण के साथ व्याख्या करें।

उत्तर दिखाएं

उत्तर

रंग उत्पन्न होता है क्योंकि ऋणायन साइटों में इलेक्ट्रॉन उपस्थित होते हैं। इन इलेक्ट्रॉनों के द्वारा दृश्य भाग के विकिरण से ऊर्जा अवशोषित कर ली जाती है और उन्हें उत्तेजित कर दिया जाता है।

उदाहरण के लिए, जब $\mathrm{NaCl}$ के क्रिस्टल को सोडियम वाष्प के वातावरण में गर्म किया जाता है, तो सोडियम अणु क्रिस्टल के सतह पर जम जाते हैं और क्रिस्टल के ऋणायन अपने सतह तक बह जाते हैं ताकि जमे हुए सोडियम अणुओं के साथ $\mathrm{NaCl}$ बन जाए। इस प्रक्रिया में, क्रिस्टल के सतह पर सोडियम अणु द्वारा इलेक्ट्रॉन खो दिए जाते हैं ताकि $\mathrm{Na}^{+}$ आयन बन जाए और इलेक्ट्रॉन ऋणायन साइट पर रह जाते हैं।

released electrons diffuse into the crystal to occupy the vacant anionic sites. These electrons get excited by absorbing energy from the visible light and impart yellow colour to the crystals.

1.22 एक ग्रुप 14 तत्व को एक उपयुक्त अशुद्धि के साथ डॉपिंग करके n-टाइप चालकता वाला अर्धचालक बनाया जाना है। इस अशुद्धि को किस ग्रुप में रखा जाना चाहिए?

उत्तर दिखाएं

Answer

n-टाइप अऊर्धचालक अतिरिक्त इलेक्ट्रॉन के उपस्थिति के कारण चालक होता है। इसलिए, एक ग्रुप 14 तत्व को एक ग्रुप 15 तत्व के साथ डॉपिंग करके $n$-टाइप अऊर्धचालक बनाया जा सकता है।

1.23 फेरोमैग्नेटिक या फेरिमैग्नेटिक कौन से पदार्थ बेहतर अनंत चुंबक बनाएंगे? अपने उत्तर की व्याख्या करें।

उत्तर दिखाएं

Answer

फेरोमैग्नेटिक पदार्थ बेहतर अनंत चुंबक बनाएंगे।

ठोस अवस्था में, फेरोमैग्नेटिक पदार्थ के धातु आयन छोटे क्षेत्रों में समूहित हो जाते हैं। इन क्षेत्रों को डोमेन कहा जाता है और प्रत्येक डोमेन एक छोटे से चुंबक के रूप में काम करता है। अनचुंबक अवस्था में फेरोमैग्नेटिक पदार्थ के डोमेन अनुकूल रूप से व्यवस्थित होते हैं। इस प्रकार, डोमेन के चुंबकीय क्षेत्र के पल कैंसिल हो जाते हैं। हालांकि, जब पदार्थ को एक चुंबकीय क्षेत्र में रखा जाता है, तो सभी डोमेन चुंबकीय क्षेत्र की दिशा में व्यवस्थित हो जाते हैं और एक मजबूत चुंबकीय प्रभाव उत्पन्न होता है।

डोमेन की व्यवस्था चुंबकीय क्षेत्र के हटाने के बाद भी बनी रहती है। इसलिए, फेरोमैग्नेटिज वस्तु एक अनंत चुंबक बन जाती है।

सारांश

ठोसों के निश्चित द्रव्यमान, आयतन और आकार होते हैं। इसका कारण उनके संघटक कणों के निश्चित स्थिति, छोटी दूरी और उनके बीच मजबूत परस्पर क्रिया है। अमोर्फस ठोसों में संघटक कणों के व्यवस्था में केवल छोटी दूरी के क्रम होते हैं और इस कारण वे अति ठंडे द्रव के समान व्यवहार करते हैं, तीव्र गलनांक नहीं होते और उनकी प्रकृति पूर्ण विषम विषमता होती है। क्रिस्टलीय ठोसों में उनके संघटक कणों के व्यवस्था में लंबी दूरी के क्रम होते हैं। वे तीव्र गलनांक वाले होते हैं, उनकी प्रकृति विषम विषमता होती है और उनके कण विशिष्ट आकार रखते हैं। क्रिस्टलीय ठोसों के गुण उनके संघटक कणों के बीच अंतर के आधार पर निर्भर करते हैं। इस आधार पर वे चार श्रेणियों में विभाजित किए जा सकते हैं, अर्थात: अणुक, आयनिक, धातुई और सहसंयोजक ठोस। इनके गुण बहुत अलग-अलग होते हैं।

क्रिस्टलीय ठोसों में संघटक कण समान आकृति में व्यवस्थित होते हैं जो क्रिस्टल के सभी भाग में फैले होते हैं। इस व्यवस्था को आमतौर पर एक तीन-आयामी बिंदुओं के आवरण के रूप में दर्शाया जाता है जिसे क्रिस्टल लैटिस कहते हैं। प्रत्येक लैटिस बिंदु अंतरिक अंतर के एक कण के स्थान को दर्शाता है। सभी में से, चौदह अलग-अलग प्रकार के लैटिस संभव हैं जिन्हें ब्रैवेस लैटिस कहते हैं। प्रत्येक लैटिस को इसके छोटे विशिष्ट भाग को दोहराकर बनाया जा सकता है जिसे यूनिट सेल कहते हैं। एक यूनिट सेल को इसके किनारों की लंबाई और इन किनारों के बीच तीन कोणों द्वारा चिह्नित किया जाता है। यूनिट सेल या तो प्राथमिक हो सकते हैं जिनमें केवल कोनों पर कण होते हैं या केंद्रित हो सकते हैं। केंद्रित यूनिट सेल में अतिरिक्त कण बॉडी सेंटर (बॉडी सेंटर्ड), प्रत्येक फेस केंद्र (फेस सेंटर्ड) या दो विपरीत फेस केंद्र (एंड सेंटर्ड) पर होते हैं। सभी में से, सात प्रकार के प्राथमिक यूनिट सेल होते हैं। केंद्रित यूनिट सेल को भी शामिल करते हुए, सभी में से चौदह प्रकार के यूनिट सेल होते हैं, जो चौदह ब्रैवेस लैटिस के निर्माण करते हैं।

कणों के सघन पैकिंग के परिणामस्वरूप दो बहुत कुशल लैटिस प्राप्त होते हैं, षष्टीय सघन पैकिंग (hcp) और घनीय सघन पैकिंग (ccp)। द्वितीय लैटिस को भी चेहरा केंद्रित घन (fcc) लैटिस के रूप में जाना जाता है। इन दोनों पैकिंग में 74% स्थान भरा होता है। शेष स्थान दो प्रकार के रिक्त स्थानों के रूप में मौजूद होता है- षष्टीय रिक्त स्थान और चतुष्कोणीय रिक्त स्थान। अन्य प्रकार के पैकिंग सघन पैकिंग नहीं होते हैं और कणों के कम कुशल पैकिंग के कारण होते हैं। जबकि शरीर केंद्रित घन लैटिस (bcc) में 68% स्थान भरा होता है, सरल घन लैटिस में केवल 52.4% स्थान भरा होता है।

ठोस अपने संरचना में पूर्ण नहीं होते। उनमें विभिन्न प्रकार के त्रुटियाँ या दोष होते हैं। बिंदु दोष और रेखा दोष आम प्रकार के दोष हैं। बिंदु दोष तीन प्रकार के होते हैं - स्टोइकियोमेट्रिक दोष, अशुद्धि दोष और अस्टोइकियोमेट्रिक दोष। रिक्तिका दोष और अंतर्गत दोष स्टोइकियोमेट्रिक बिंदु दोष के दो मूल प्रकार हैं। आयनिक ठोस में ये दोष फ्रेंकल और शॉट्टकी दोष के रूप में उपस्थित होते हैं। अशुद्धि दोष क्रिस्टल में अशुद्धि की उपस्थिति के कारण होते हैं। आयनिक ठोस में जब आयनिक अशुद्धि मुख्य यौगिक के तुलना में अलग वैलेंस का होता है, तो कुछ रिक्तिका बनती है। अस्टोइकियोमेट्रिक दोष धातु अधिकता प्रकार और धातु कमी प्रकार के होते हैं। कभी-कभी चालनीय गुणों को बदलने के लिए अर्धचालक में गणित के अनुसार अशुद्धियों को प्रवेश कराया जाता है। ऐसे अवयव इलेक्ट्रॉनिक्स उद्योग में व्यापक रूप से उपयोग किए जाते हैं। ठोस कई प्रकार के चुंबकीय गुण दिखाते हैं जैसे कि पैरामैग्नेटिज्म, डायमैग्नेटिज्म, फेरोमैग्नेटिज्म, एंटीफेरोमैग्नेटिज्म और फेरिमैग्नेटिज्म। इन गुणों का उपयोग ऑडियो, वीडियो और अन्य रिकॉर्डिंग उपकरणों में किया जाता है। इन सभी गुणों को उनके इलेक्ट्रॉनिक विन्यास या संरचना के साथ संबंधित किया जा सकता है।