वेक्टर बीजगणित प्रश्न 2
प्रश्न 2 - 2024 (01 फरवरी शिफ्ट 2)
एक $\triangle ABC$ में $A(1,2,3), B(-2,8,0)$ और $C(3,6,7)$ हैं। यदि $\angle BAC$ के कोण अर्धक रेखा $BC$ को बिंदु $D$ पर मिलता है, तो वेक्टर $\overrightarrow{A D}$ के वेक्टर $\overrightarrow{A C}$ पर प्रक्षेप की लंबाई है:
(1) $\dfrac{37}{2 \sqrt{39}}$
(2) $\dfrac{\sqrt{38}}{2}$
(3) $\dfrac{39}{2 \sqrt{38}}$
(4) $\sqrt{19}$
उत्तर दिखाएं
उत्तर (1)
समाधान
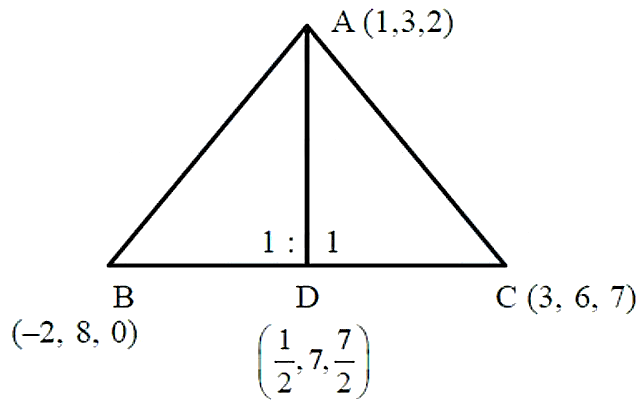
$ D \left(\dfrac{1}{2}, 7, \dfrac{7}{2}\right) $
$A(1,3,2) ; B(-2,8,0) ; C(3,6,7)$;
$\overrightarrow{AC}=2 \hat{i}+3 \hat{j}+5 \hat{k}$
$\overrightarrow{AB}=-3 \hat{i}+5 \hat{j}-2 \hat{k}$
$AB=\sqrt{9+25+4}=\sqrt{38}$
$AC=\sqrt{4+9-25}=\sqrt{38}$
$\overrightarrow{AD}=-\dfrac{1}{2} \hat{i}+4 \hat{j}+\dfrac{3}{2} \hat{k}=\dfrac{1}{2}(-\hat{i}+8 \hat{j}+3 \hat{k})$
वेक्टर $\overrightarrow{AD}$ के वेक्टर $\overrightarrow{AC}$ पर प्रक्षेप की लंबाई
$=\left|\dfrac{\overrightarrow{AD} \cdot \overrightarrow{AC}}{|\overrightarrow{AC}|}\right|=\dfrac{37}{2 \sqrt{38}}$





