त्रिविमीय ज्यामिति प्रश्न 9
प्रश्न 9 - 2024 (27 जनवरी शिफ्ट 2)
एक त्रिभुज के शीर्ष $A, B$ और $C$ के स्थिति सदिश $2 \hat{i}+2 \hat{j}+\hat{k},\hat{i}+2 \hat{j}+2 \hat{k}$ और $2 \hat{i}+\hat{j}+2 \hat{k}$ हैं। मान लीजिए $l _1, l _2$ और $l _3$ त्रिभुज के लंबकेंद्र से भुजाओं $AB, BC$ और $CA$ पर डाले गए लंबों की लंबाई हैं, तो $l _1^{2}+l _2^{2}+l _3^{2}$ के बराबर है:
(1) $\frac{1}{5}$
(2) $\frac{1}{2}$
(3) $\frac{1}{4}$
(4) $\frac{1}{3}$
उत्तर दिखाएं
उत्तर (2)
समाधान
$\triangle ABC$ समबाहु है
लंबकेंद्र और गुरुत्वकेंद्र एक ही बिंदु पर स्थित होंगे
$G\left(\frac{5}{3}, \frac{5}{3}, \frac{5}{3}\right)$
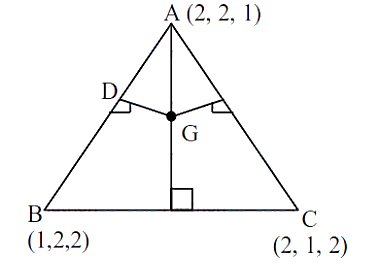
$AB$ का मध्य बिंदु $D$ $\left(\frac{3}{2}, 2, \frac{3}{2}\right)$ है
$\therefore \ell _1=\sqrt{\frac{1}{36}+\frac{1}{9}+\frac{1}{36}}$
$\ell _1=\sqrt{\frac{1}{6}}=\ell _2=\ell _3$
$\therefore \ell _1^{2}+\ell _2^{2}+\ell _3^{2}=\frac{1}{2}$





