वृत्त प्रश्न 8
प्रश्न 8 - 2024 (30 जनवरी शिफ्ट 2)
दो वृत्त $C _1: x^{2}+y^{2}=25$ और $C _2:(x-\alpha)^{2}+y^{2}=16$, जहाँ $\alpha \in(5,9)$ लें। मान लीजिए $C _1$ और $C _2$ के एक उभयनिष्ठ बिंदु से खींचे गए दो त्रिज्याओं (एक वृत्त के लिए प्रत्येक) के बीच का कोण $\sin ^{-1}\left(\frac{\sqrt{63}}{8}\right)$ है। यदि $C _1$ और $C _2$ के उभयनिष्ठ जीवा की लंबाई $\beta$ है, तो $(\alpha \beta)^{2}$ का मान है
उत्तर दिखाएं
उत्तर (1575)
समाधान
$C _1: x^{2}+y^{2}=25, C _2:(x-\alpha)^{2}+y^{2}=16$
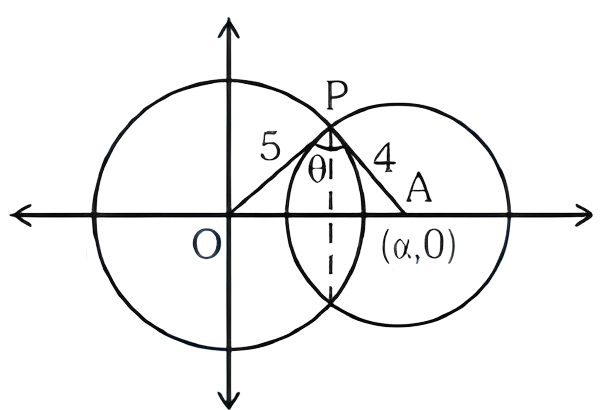
$5<\alpha<9$
$\theta=\sin ^{-1}\left(\frac{\sqrt{63}}{8}\right)$
$\sin \theta=\frac{\sqrt{63}}{8}$
$\triangle OAP$ का क्षेत्रफल $=\frac{1}{2} \times \alpha\left(\frac{\beta}{2}\right)=\frac{1}{2} \times 5 \times 4 \sin \theta$
$\Rightarrow \alpha \beta=40 \times \frac{\sqrt{63}}{8}$
$\alpha \beta=5 \times \sqrt{63}$
$(\alpha \beta)^{2}=25 \times 63=1575$





