वृत्त प्रश्न 3
प्रश्न 3 - 2024 (01 फरवरी शिफ्ट 2)
वृत्त $x^{2}+(y-1)^{2}=1$ के ऐसे जीवाओं के मध्य बिंदुओं के बिंदुपथ के रेखा $x+y=1$ पर बिंदु $P$ और $Q$ पर प्रतिच्छेदन होता है। तब, $PQ$ की लंबाई है:
(1) $\frac{1}{\sqrt{2}}$
(2) $\sqrt{2}$
(3) $\frac{1}{2}$
(4) 1
उत्तर दिखाएं
उत्तर (1)
समाधान

$m _{OM} \cdot m _{CM}=-1$
$\frac{k}{h} \cdot \frac{k-1}{h}=-1$
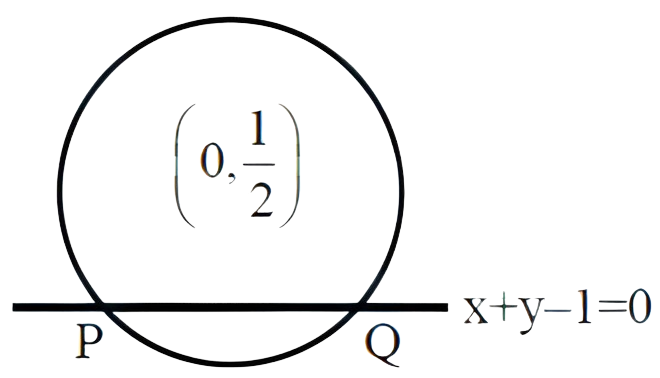
$\therefore$ बिंदुपथ $x^{2}+y(y-1)=0$
$x^{2}+y^{2}-y=0$ $p=\left|\frac{1 / 2}{\sqrt{2}}\right| p=\frac{1}{2 \sqrt{2}}$
$PQ=2 \sqrt{r^{2}-p^{2}}$
$=2 \sqrt{\frac{1}{4}-\frac{1}{8}}=\frac{1}{\sqrt{2}}$





