फंक्शन प्रश्न 19
प्रश्न 19 - 31 जनवरी - शिफ्ट 2
मान लीजिए $f: \mathbb{R}-\lbrace 2,6\rbrace \to \mathbb{R}$ एक वास्तविक मान फंक्शन है जो $f(x)=\frac{x^{2}+2 x+1}{x^{2}-8 x+12}$ द्वारा परिभाषित है। तब $f$ की परिसर है
(1) $(-\infty,-\frac{21}{4}] \cup[0, \infty)$
(2) $(-\infty,-\frac{21}{4}) \cup(0, \infty)$
(3) $(-\infty,-\frac{21}{4}] \cup[\frac{21}{4}, \infty)$
(4) $(-\infty,-\frac{21}{4}] \cup[1, \infty)$
उत्तर दिखाएं
उत्तर: (1)
समाधान:
सूत्र: फंक्शन पर ऑपरेशन , फंक्शन की परिसर , द्विघात समीकरण के मूलों की प्रकृति
मान लीजिए $y=\frac{x^{2}+2 x+1}{x^{2}-8 x+12}$
क्रॉस गुणा करके
$yx^{2}-8 xy+12 y-x^{2}-2 x-1=0$
$x^{2}(y-1)-x(8 y+2)+(12 y-1)=0$
केस 1: $ y \neq 1$
$D \geq 0$
$\Rightarrow(8 y+2)^{2}-4(y-1)(12 y-1) \geq 0$
$\Rightarrow y(4 y+21) \geq 0$
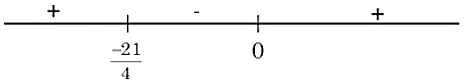
$y \in(-\infty, \frac{-21}{4}] \cup[0, \infty)-{1}$
केस 2: $y=1$
$ \begin{aligned} & x^{2}+2 x+1=x^{2}-8 x+12 \\ & 10 x=11 \\ & x=\frac{11}{10} \quad \text{ इसलिए, } y \text{ 1 हो सकता है} \end{aligned} $
इसलिए, $f$ की परिसर $(-\infty,-\frac{21}{4}] \cup[0, \infty)$ है





