तीव्रता की तरंगों का हस्तक्षेप $I_{1}$ और $I_{2}$ :

परिणामी तीव्रता,

$I=I_1+I_2+2\sqrt{I_1I_2}\hspace{2mm}COS(\Delta\phi)$

कहाँ, $\Delta \phi=$ चरण अंतर.

रचनात्मक हस्तक्षेप के लिए: $\quad I_{\max }=\left(\sqrt{I_{1}}+\sqrt{I_{2}}\right)^{2}$

विनाशकारी हस्तक्षेप के लिए: $\quad I_{\min }=\left(\sqrt{I_{1}}-\sqrt{I_{2}}\right)^{2}$

यदि स्रोत असंगत हैं: $\quad I=I_1+I_2$, प्रत्येक बिंदु पर।

YDSE :

पथ अंतर, $\Delta p=S_{2} P-S_{1} P=d \sin \theta$

$\begin{array}{ll}\text { if } & d<D D \quad=\frac{d y}{D} \\ \text { if } & y<D\end{array}$

मैक्सिमा के लिए,

$\Delta p=n \lambda \quad \Rightarrow \quad y=n \beta \quad n=0, \pm 1, \pm 2 \ldots \ldots$.

मिनिमा के लिए

$ \शुरू{संरेखित} और \Delta p=\quad \Delta p= \begin{cases}(2 n-1) \frac{\lambda}{2} और n=1,2,3 \ldots \ldots \ldots \ldots। \\ (2 n+1) \frac{\lambda}{2} & n=-1,-2,-3 \ldots \ldots \ldots\end{cases} \\ \\ और \राइटएरो \quad y= \begin{cases}(2 n-1) \frac{\beta}{2} और n=1,2,3 \ldots \ldots \ldots \ldots। \\ (2 n+1) \frac{\beta}{2} और n=-1,-2,-3 \ldots \ldots। .\end{मामले} \अंत{संरेखित} $

जहां, फ्रिंज चौड़ाई $\beta=\frac{\lambda D}{d}$

यहाँ, $\lambda=$ माध्यम में तरंग दैर्ध्य.

उच्चतम ऑर्डर मैक्सिमा: $\quad \mathrm{n}_{\max }=\left[\frac{\mathrm{d}}{\lambda}\right]$

मैक्सिमा की कुल संख्या $=2 \mathrm{n}_{\max }+1$

उच्चतम ऑर्डर मिनिमा: $\quad \mathrm{n}_{\max }=\left[\frac{\mathrm{d}}{\lambda}+\frac{1}{2}\right]$

मिनिमा की कुल संख्या $=2 \mathrm{n}_{\max }$.

स्क्रीन पर तीव्रता:

$\quad I=I_{1}+I_{2}+2 \sqrt{I_{1} I_{2}} \cos (\Delta \phi)$ कहाँ, $\Delta \phi=\frac{2 \pi}{\lambda} \Delta p$

अगर $I_1=I_2,\quad{I=41_1} \hspace{6mm}COS^2(\frac{\Delta\phi}{2})$

YDSE दो तरंग दैर्ध्य के साथ $\lambda_{1} $&$ \lambda_{2}$ :

केंद्रीय उच्चिष्ठ का निकटतम बिंदु जहां चमकीली फ्रिजें संपाती होती हैं:

$ y = n_ $

केंद्रीय उच्चिष्ठ का निकटतम बिंदु जहां दो गहरे किनारे संपाती होते हैं,

$$ \left.y=\left(n_{1}-\frac{1}{2}\right) \beta_{1}=n_{2}-\frac{1} } $$

ऑप्टिकल पथ अंतर

तिरछी घटना के साथ YDSE

YDSE में, किरण स्लिट पर के झुकाव पर आपतित होती है $\theta_{0}$ प्रायोगिक सेट-अप की समरूपता की धुरी पर

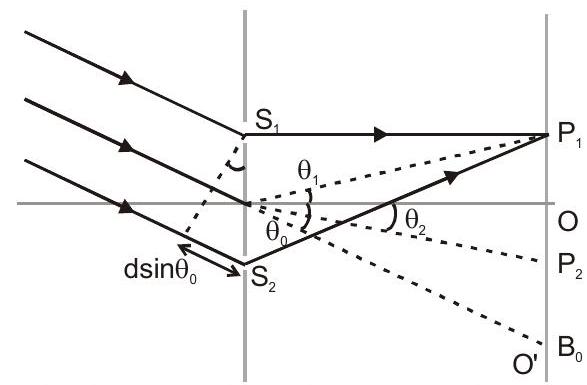
हम एक बिंदु पर केंद्रीय उच्चिष्ठ प्राप्त करते हैं, जहां, $\Delta p=0$.

$$ \text { या } \quad \theta_{2}=\theta_{0} \text {. } $$

यह बात से मेल खाती है $\mathrm{O}^{\prime}$ आरेख में.

इसलिए हमारे बीच पथ भिन्नता है।

पतली-फिल्म हस्तक्षेप

परावर्तित प्रकाश में हस्तक्षेप के लिए $\quad 2 \mu \mathrm{d}$

$= \begin{cases}n \lambda & \text { for destructive interference } \\ \left(n+\frac{1}{2}\right) \lambda & \text { for constructive interference }\end{cases}$

संचरित प्रकाश में हस्तक्षेप के लिए $\quad 2 \mu \mathrm{d}$

$= \begin{cases}n \lambda & \text { for constructive interference } \\ \left(n+\frac{1}{2}\right) \lambda & \text { for destructive interference }\end{cases}$

ध्रुवीकरण

• $\mu=\tan$.(ब्रूस्टर का कोण)

$\theta \rho+\theta_{r}=90^{\circ}$ (परावर्तित और अपवर्तित किरणें परस्पर लंबवत होती हैं।)

• मालुस का नियम।

$\mathrm{I}=\mathrm{I}_{0} \cos ^{2}$

$\mathrm{I}=\mathrm{KA}^{2} \cos ^{2}$

-ऑप्टिकल गतिविधि

$[\alpha]_{t}^{\lambda}{ }^{\circ} \mathrm{C}=\frac{\theta}{\mathrm{L} \times \mathrm{C}}$

$\theta=$ लंबाई में घूमना $L$ एकाग्रता पर $C$.

विवर्तन

• $\quad a \sin \theta=(2 m+1) / 2$ मैक्सिमा के लिए. कहाँ $m=1,2,3 \ldots \ldots$
• $\quad \sin \theta=\frac{m \lambda}{a}, m= \pm 1, \pm 2, \pm 3 \ldots \ldots \ldots$. मिनिमा के लिए.
• केंद्रीय मैक्सिमा की रैखिक चौड़ाई $=\frac{2 \mathrm{~d} \lambda}{\mathrm{a}}$
• $\quad$ केंद्रीय मैक्सिमा की कोणीय चौड़ाई $=\frac{2 \lambda}{a}$
• $\quad I=I_{0}\left[\frac{\sin \beta / 2}{\beta / 2}\right]^{2}$ कहाँ $\beta=\frac{\pi a \sin \theta}{\lambda}$

सुलझाने की शक्ति

$ \mathrm{R}=\frac{\lambda}{\lambda_{2}-\lambda_{1}}=\frac{\lambda}{\Delta \lambda} $

$ \text {कहां, } \lambda=\frac{\lambda_{1}+\lambda_{2}}{2}, \Delta \lambda=\lambda_{2}-\lambda_{1} $