1. सख्त शरीर :

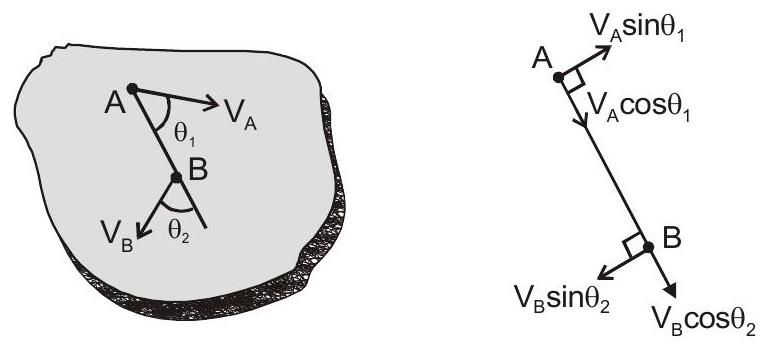
यदि उपरोक्त पिंड कठोर है

$ V_A \cos \theta_1=V_B \cos \theta_2 $

$V_{B A}=$ बिंदु का सापेक्ष वेग $B$ बिंदु के संबंध में $A$.

2. जड़ता का क्षण (I) :

परिभाषा: जड़त्व क्षण को किसी पिंड की घूर्णी गति में उत्पन्न परिवर्तन का विरोध करने की प्रणाली की क्षमता के रूप में परिभाषित किया गया है।

जड़त्व क्षण एक अदिश धनात्मक राशि है।

$ मैं =mr_{1}^{2}+m_{2}r_{2}^{2}+\ldots\ldots $

$ =I_1+I_2+I_3+\ldots \ldots \ldots $

जड़त्व आघूर्ण की SI इकाई है $\mathrm{Kgm}^{2}$.

का जड़त्व आघूर्ण :

2.1 एक एकल कण: $\mathrm{I}=\mathrm{mr}^{2}$

कहाँ $m=$ कण का द्रव्यमान

$r=$ जड़ता के किस क्षण की गणना करने के लिए अक्ष से कण की लंबवत दूरी की गणना की जानी है

2.2 अनेक कणों के लिए (कणों की प्रणाली):

$$ I=\sum_{i=1}^{n} m_{i} r_{i}^{2} $$

2.3 एक सतत वस्तु के लिए:

$\mathrm{I}=\int \mathrm{dmr} \mathrm{r}^{2}$

कहाँ $\mathrm{dm}=$ एक छोटे तत्व का द्रव्यमान

$r=$ अक्ष से कण की लंबवत दूरी

2.4 किसी बड़ी वस्तु के लिए:

$\mathrm{I}=\int \mathrm{dI} \mathrm{I}_{\text {element }}$

कहाँ $\mathrm{dI}=$ एक छोटे तत्व की जड़ता का क्षण

3. जड़ता के क्षण पर दो महत्वपूर्ण प्रमेय:

3.1 लंबवत अक्ष प्रमेय

[केवल समतल लैमिना पर लागू (अर्थात् केवल 2-डी वस्तुओं के लिए)]।

$I_{z}=I_{x}+I_{y} \quad$ (जब वस्तु अंदर हो $x-y$ विमान)।

3.2 समानांतर अक्ष प्रमेय

(किसी भी प्रकार की वस्तु पर लागू):

$I_{AB}=I_{cm}+Md^{2}$

कुछ उपयोगी सूत्रों की सूची:

4. आवर्तन का अर्ध व्यास :

$\mathrm{I}=\mathrm{MK}^{2}$

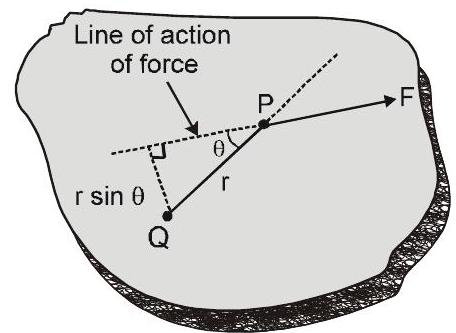
5 टॉर्क :

$\vec{\tau}=\vec{r} \times \vec{F}$

5.5 के बीच संबंध ’ $\tau$ ’ & ’ $\alpha$ ’ (टिका हुई वस्तु या शुद्ध घूर्णन के लिए)

$ \vec{\tau_{ext\Big)Hinge }}$ $ = I_{Hinge} \vec{\alpha}$

कहाँ $\vec{\tau_{ext\Big)Hinge }}$=$ काज बिंदु के चारों ओर शरीर पर कार्य करने वाला शुद्ध बाह्य बल आघूर्ण

$\mathrm{I}_{\text {Hinge }}=$ काज बिंदु के बारे में शरीर की जड़ता का क्षण

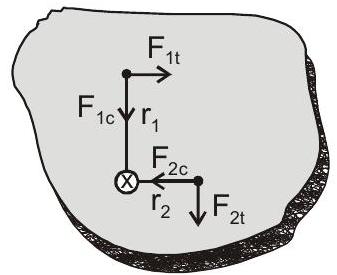
$F_{1t}=M_{1} a_{1t}=M_1 r_1 \alpha$

$F_{2 t}=M_{2} a_{2 t}=M_{2} r_{2} \alpha$

$\tau_{resultant}=F_{1t} r_{1}+F_{2t} r_{2}+\ldots \ldots \ldots$

$=M_{1} \alpha r_{1}^{2}+M_{2} \alpha r_{2}^{2}+$

$\left.\tau_{\text {resultant }}\right)_{\text {external }}=\mathrm{I} \alpha$

घूर्णी गतिज ऊर्जा $=\frac{1}{2} \cdot$ मैं। $\omega^{2}$

$\overrightarrow{P}=M\vec{v}_{CM} \Rightarrow $

$ \overrightarrow{F_{external}}=$ $M \overrightarrow{a}_{CM} $

शरीर पर कार्य करने वाले शुद्ध बाह्य बल के दो भाग होते हैं स्पर्शरेखीय और अभिकेन्द्रीय।

$ \Rightarrow \quad F_C = ma_C = m \frac{v^2}{r_{CM}}=m $ $\omega^{2} $ $ r_{cm} $

$ \Rightarrow \quad F_t = ma_t = $ $m\alpha r_{CM}$

6. घूर्णी संतुलन:

अनुवादात्मक संतुलन के लिए.

$ \सिग्मा F_{x}=0 \hspace{10mm}…(i) $

और $\quad \Sigma \mathrm{F}_{\mathrm{y}}=0 \hspace{10mm}…(ii)$

घूर्णी संतुलन की स्थिति है

$ \सिग्मा \Gamma_{z}=0 $

7. कोनेदार गति $(\vec{L})$

7.1 एक बिंदु के चारों ओर एक कण का कोणीय संवेग।

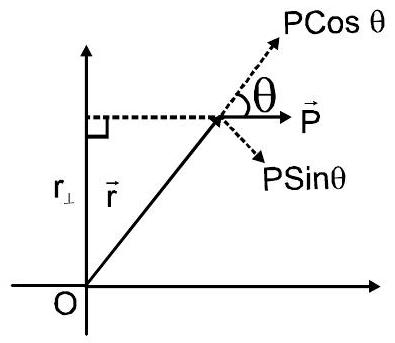
$ \ओवरराइटएरो{L} =\ओवरराइटएरो{r} \times \ओवरराइटएरो{P} \quad \राइटएरो \quad L=rpsin \theta $

$ |\ओवरराइटएरो{L}| =r_{\perp} \times P $

|$\ओवरराइटएरो{L}| =P_{\perp} \times r $

7.3 स्थिर अक्ष के परितः घूमते किसी कठोर पिंड का कोणीय संवेग:

$ \overrightarrow{L_{H}}=I_{H} \vec{\omega} $

$\mathrm{L}_{\mathrm{H}}=$ अक्ष के परितः वस्तु का कोणीय संवेग $\mathrm{H}$.

$\mathrm{I}_{\mathrm{H}}=$ अक्ष के परितः कठोर वस्तु का जड़त्व आघूर्ण $\mathrm{H}$.

$\omega=$ वस्तु का कोणीय वेग.

7.4 कोणीय संवेग का संरक्षण

किसी कण या निकाय का कोणीय संवेग स्थिर रहता है यदि $\tau_{\mathrm{ext}}=0$ उस बिंदु या घूर्णन अक्ष के बारे में।

7.5 टॉर्क और कोणीय संवेग के बीच संबंध

$ \vec{\tau}=\frac{\mathrm{d} \overrightarrow{\mathrm{L}}}{\mathrm{dt}} $

टॉर्क कोणीय गति में परिवर्तन है

7.6 टॉर्क का आवेग:

$ \int \tau dt=\Delta J \quad \quad \डेल्टा जे \दायां तीर \पाठ {कोणीय गति में परिवर्तन। } $

किसी कठोर पिंड के लिए, उसकी गति के दौरान कणों के बीच की दूरी अपरिवर्तित रहती है $\mathrm{r}_{\mathrm{P} / \mathrm{Q}}=$ स्थिर

वेगों के लिए

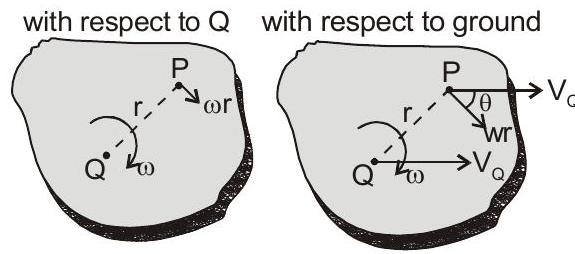
$V_P=\sqrt{V_Q^{2}+(\omega r)^{2}+2 V_Q \omega r \cos \theta}$

त्वरण के लिए:

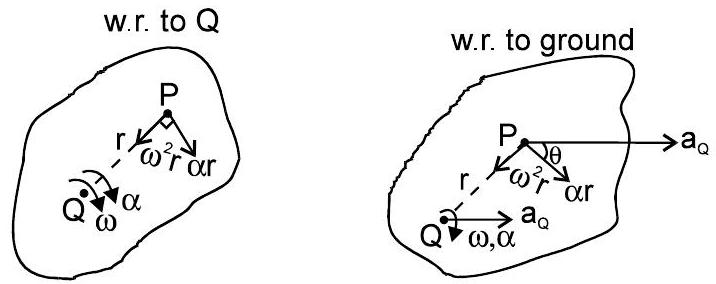
$\theta, \omega, \alpha$ शरीर के प्रत्येक बिंदु (या शरीर से मजबूती से जुड़ा हुआ कोई अन्य बाहरी बिंदु) के बारे में समान हैं।

गतिशीलता:

$ \vec{\tau_{cm}}=I_{cm} \vec{\alpha}, $

$\overrightarrow F_{ext} = M \overrightarrow{a}_{cm}$

$\overrightarrow{P_{system}}$ $=M \overrightarrow{v}_{cm}$,

कुल के.ई $\quad=\frac{1}{2} M_{\mathrm{cm}^{2}}+\frac{1}{2} \mathrm{I}_{\mathrm{cm}} \omega^{2}$

कोणीय संवेग अक्ष $A B=\vec{L}$ सीएम के बारे में $+\vec{L}$ सीएम के बारे में $A B$

$\vec{L}_{AB}$

$= I_{cm}\vec{\omega}+\vec{r_{cm}}\times M\vec{v}_{cm}$

सरल आवर्त गति

एसएचएम

$\mathrm{F}=-\mathrm{kx}$

SHM का सामान्य समीकरण है $x=A \sin (\omega t+\phi) ;(\omega t+\phi)$ गति का चरण है और $\phi$ गति का प्रारंभिक चरण है.

कोणीय आवृत्ति$(\omega)$ : $ \omega=\frac{2 \pi}{T}=2 \pi f $

समय सीमा $(\mathrm{T})$ :$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}} $

रफ़्तार :$v=\omega \sqrt{A^{2}-x^{2}} $

त्वरण: $ a=-\omega^{2} x$

गतिज ऊर्जा (केई): $\quad \frac{1}{2} m v^{2}=\frac{1}{2} m \omega^{2}\left(A^{2}-x^{2}\right)=\frac{1}{2} k\left(A^{2}-x^{2}\right)$

संभावित ऊर्जा (पीई): $\quad \frac{1}{2} \mathrm{Kx}{ }^{2}$

कुल यांत्रिक ऊर्जा (टीएमई)

$=K . E .+P . E .=\frac{1}{2} k\left(A^{2}-x^{2}\right)+\frac{1}{2} K x^{2}=\frac{1}{2} K A^{2}$ (जो स्थिर है)

स्प्रिंग-मास प्रणाली

(1)

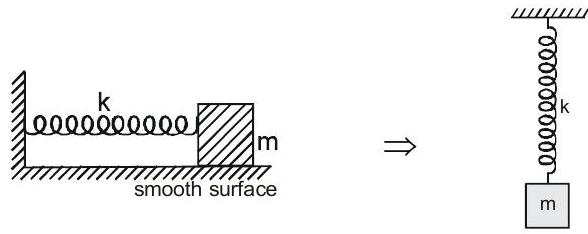
$$ \दायाँ तीर \quad T=2 \pi \sqrt{\frac{m}{k}} $$

(2)

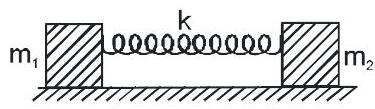
$T=2 \pi \sqrt{\frac{\mu}{K}}$, कहाँ $\mu=\frac{m_1 m_2}{\left(m_1+m_2\right)}$ घटे हुए द्रव्यमान के रूप में जाना जाता है

स्प्रिंग्स का संयोजन

श्रृंखला संयोजन: $\quad 1 / k_{eq}=1 / k_{1}+1 / k_{2}$

समानांतर संयोजन: $\quad k_{eq}=k_1+k_2$

सरल पेंडुलम $T=2 \pi \sqrt{\frac{\ell}{g}}=2 \pi \sqrt{\frac{\ell}{g_{\text {eff. }}}}$ (संदर्भ फ़्रेम को तेज़ करने में); $g_{\text {eff }}$ छद्म बल और गुरुत्वाकर्षण बल के कारण शुद्ध त्वरण है।

यौगिक पेंडुलम / भौतिक पेंडुलम

समय सीमा $(T): \quad T=2 \pi \sqrt{\frac{\mathrm{I}}{\mathrm{mg} \ell}}$

कहाँ, $\mathrm{I}=\mathrm{I}_{\mathrm{CM}}+\mathrm{m} \ell^{2} ; \ell$ निलंबन बिंदु और द्रव्यमान केंद्र के बीच की दूरी है।

मरोड़ वाला पेंडुलम

समय सीमा $(T): \quad T=2 \pi \sqrt{\frac{I}{C}} \quad$ कहाँ, $C=$ मरोड़ स्थिरांक

एक ही दिशा में एसएचएम का सुपरपोजिशन

$x_{1}=A_{1} \sin \omega t \quad$ & $\क्वाड x_{2}=A_{2} \sin (\omega t+\theta) $

यदि परिणामी का समीकरण $\mathrm{SHM}$ के रूप में लिया जाता है $\mathrm{x}=\mathrm{A} \sin (\omega \mathrm{t}+\phi)$ $A=\sqrt{A_{1}^{2}+A_{2}^{2}+2 A_{1} A_{2} \cos \theta}$ &$ \quad \tan \phi=\frac{A_{2} \sin \theta}{A_{1}+A_{2} \cos \theta}$

1. नम दोलन

-अवमंदन बल

$\overrightarrow{\mathrm{F}}=-\mathrm{b} \overrightarrow{\mathrm{v}}$

-गति का समीकरण है

$\frac{\mathrm{mdv}}{\mathrm{dt}}=-\mathrm{kx}-\mathrm{bv}$

• $b^{2}-4 m K>0$ अत्यधिक भीगना
• $b^{2}-4 m K=0$ गंभीर अवमंदन
• $b^{2}-4 m K<0$ भिगोना के तहत
• छोटे भिगोने के लिए समाधान प्रपत्र का है.

$x=\left(A_{0} e^{-b t / 2 m}\right) \sin \left[\omega^{1} t+\delta\right]$, कहाँ $\omega^{\prime}=\sqrt{\left(\frac{k}{m}\right)-\left(\frac{b}{2 m}\right)^{2}}$

छोटे बी के लिए

• कोणीय आवृत्ति $\omega^{\prime} \approx \sqrt{\mathrm{k} / \mathrm{m}},=\omega_{0}$

• आयाम $A=A_{0} e^{\frac{-b t}{2 m}}$

• ऊर्जा $E(t)=\frac{1}{2} K A^{2} e^{-b t / m}$

• गुणवत्ता कारक या $Q$ कीमत, $Q=2 \pi \frac{E}{|\Delta E|}=\frac{\omega^{\prime}}{2 \omega_{Y}}$

कहाँ $, \omega^{\prime}=\sqrt{\frac{k}{m} \cdot \frac{b^{2}}{4 m^{2}}} \quad, \omega_{Y}=\frac{b}{2 m}$

2. जबरन दोलन और अनुनाद

बाहरी बल $F(t)=F_{0} \cos \omega_{d} t$

$x(t)=A \cos \left(\omega_{d} t+\phi\right)$

$A=\frac{F_{0}}{\sqrt{\left(m^{2}\left(\omega^{2}-\omega_{d}^{2}\right)^{2}+\omega_{d}^{2} b^{2}\right)}}$ और $\tan \phi=\frac{-v_{0}}{\omega_{d} x_{0}}$

(ए) छोटी डंपिंग $A=\frac{F_{0}}{m\left(\omega^{2}-\omega_{d}^{2}\right)}$

(बी) ड्राइविंग आवृत्ति प्राकृतिक आवृत्ति के करीब $A=\frac{F_{0}}{\omega_{d} b}$