$ \overrightarrow{V_{AB}} $ (बी के संबंध में ए का वेग) $ = \overrightarrow{V_A} - \overrightarrow{V_B} $

$ \overrightarrow{a_{AB}} $ (बी के संबंध में ए का त्वरण) = $ \overrightarrow{a_A} - \overrightarrow{a_B} $

सीधी रेखा के अनुदिश सापेक्ष गति -
$ \overrightarrow{x_{BA}} = \overrightarrow{x_{B}} -\overrightarrow{x_{A}} $

नदी पार करना

नदी में एक नाव या आदमी हमेशा नाव (या आदमी) के वेग और नदी के प्रवाह के वेग के परिणामी वेग की दिशा में चलता है।

1. सबसे कम समय :

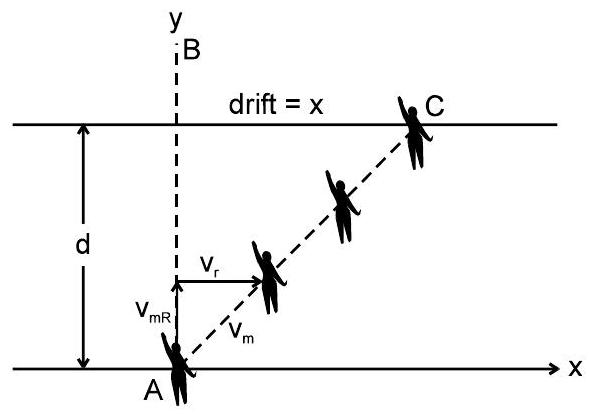
नदी के किनारे वेग, $v_{x}=v_{R}$.

नदी के लंबवत वेग, $v_{f}=v_{m R}$

नेट स्पीड किसके द्वारा दी जाती है? $v_{m}=\sqrt{v_{m R}^{2}+v_{R}^{2}}$

2. सबसे छोटा रास्ता :

नदी के किनारे वेग, $\mathrm{v}_{\mathrm{x}}=0$

और वेग नदी के लंबवत् है $v_{y}=\sqrt{v_{m R}^{2}-v_{R}^{2}}$

नेट स्पीड किसके द्वारा दी जाती है? $v_{m}=\sqrt{v_{m R}^{2}-v_{R}^{2}}$

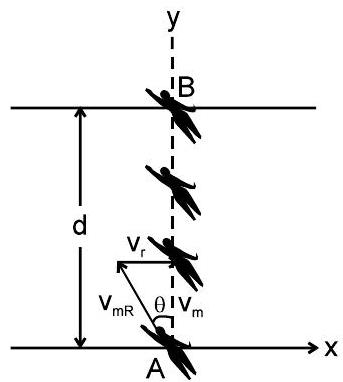
के कोण पर $90^{\circ}$ नदी की दिशा के साथ.

वेग $v_{y}$ इसका उपयोग केवल नदी पार करने के लिए किया जाता है, इसलिए नदी पार करने का समय आ गया है, $t=\frac{d}{v_{y}}=\frac{d}{\sqrt{v_{m R}^{2}-v_{R}^{2}}}$ और वेग $\mathrm{v}_{\mathrm{x}}$ शून्य है, इसलिए, इस मामले में बहाव शून्य होना चाहिए।

$\Rightarrow \quad v_{R}-v_{m R} \sin \theta=0 \quad$ या $\quad v_{R}=v_{m R} \sin \theta$

या $\quad \theta=\sin ^{-1}\left(\frac{v_{R}}{v_{m R}}\right)$

बारिश की समस्या

$ \vec{v}_{Rm} = \vec{v}_R - \vec{v}_m $

$ or \quad v_{R m}=\sqrt{v_{R^2} + v_{m^2}}$