औसत वेग (एक अंतराल में):

$ v_{av} = \overline{v} = \langle v \rangle = \frac{ \text{Total displacement}}{\text{ Total time taken}} = \frac{\overrightarrow{\mathrm{r_f}} - \overrightarrow{\mathrm{r_i}}}{\Delta t} $

औसत गति (एक अंतराल में)

$ औसत गति =\frac{ \text{यात्रा की गयी कुल दूरी} }{ \text{ लिया गया कुल समय }} $

तात्कालिक वेग (एक पल में):

$ \overrighterror{\mathrm{v}}_{\mathrm{inst}}=\lim _{\Delta \mathrm{t} \rightarrow 0}\left(\frac{\Delta \overrightarrow{\mathrm{r}} }{\डेल्टा \mathrm{t}}\दाएं) $

औसत त्वरण (एक अंतराल में):

$ v_{av} = \frac{\Delta \overrightarrow{v}}{\Delta t} = \frac{\overrightarrow{v_f} - \overrightarrow{v_i}}{\Delta t} $

तात्कालिक त्वरण (एक पल में):

$ \vec{a}=\frac{d \vec{v}}{dt}=\lim _{\Delta t \rightarrow 0}\left(\frac{\overrightarrow{\Delta v}}{\Delta t} \सही) $

एक सीधी रेखा के साथ समान रूप से त्वरित गति में ग्राफ़ $(a \neq 0)$

• $\quad x$ के संदर्भ में एक द्विघात बहुपद है $t$. इस तरह $x-t$ ग्राफ एक परवलय है.

xt ग्राफ़

वीटी ग्राफ

• $v$ के संदर्भ में एक रैखिक बहुपद है $t$. इस तरह $v-t$ ग्राफ़ ढलान की एक सीधी रेखा है।

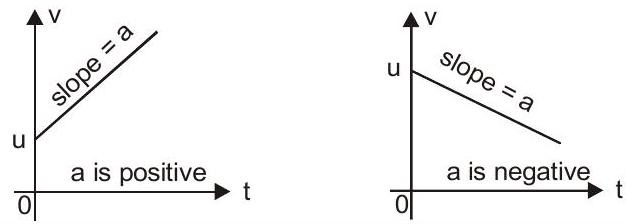
ग्राफ़ पर

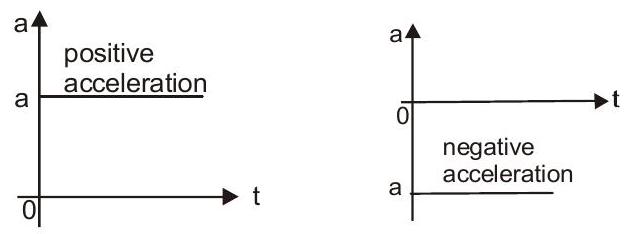
• ग्राफ़ पर एक क्षैतिज रेखा है क्योंकि a स्थिर है।

मैक्सिमा & मिनिमा

$\frac{dy}{dx} = 0 \frac{d}{dx}(\frac{dy}{dx})<0 $अधिकतम पर

और $\frac{dy}{dx} = 0 (\frac{dy}{dx}) < $मिनिमा पर.

गति के समीकरण (निरंतर त्वरण के लिए)

(ए) $\quad v=u+a t$

(बी) $\quad s=u t+\frac{1}{2}$ पर $^{2} \quad s=v t-\frac{1}{2}$ पर ${ }^{2} \quad x_{f}=x_{i}+u t+\frac{1}{2} a t^{2}$

(सी) $\quad v^{2}=u^{2}+2 a s$

(डी) $\mathrm{s}=\frac{(\mathrm{u}+\mathrm{v})}{2} \mathrm{t}$

(इ) $\quad s_{n}=u+\frac{a}{2}(2 n-1)$

स्वतंत्र रूप से गिरने वाले पिंडों के लिए: $(u=0)$

(ऊपर की दिशा को सकारात्मक मानते हुए)

(ए) $\mathrm{v}=-\mathrm{gt}$

(बी) $\mathrm{s}=-\frac{1}{2} \mathrm{gt}^{2} \hspace{10mm}\mathrm{s}=\mathrm{vt}+\frac{1}{2} \mathrm{gt}^{2} \hspace{10mm}h_{f}=h_{i}-\frac{1}{2} g t^{2}$

(सी) $v^{2}=-2 g s$

(डी) $\quad s_{n}=-\frac{g}{2}(2 n-1)$