1. गति के तीसरे नियम से

$\overrightarrow{F_{AB}} = -\overrightarrow{F_{BA}} $

$ \overrightarrow{\mathrm{F}}_{\mathrm{AB}}=\text { Force on } \mathrm{A} \text { due to } \mathrm{B} $

$\overrighterror{\mathrm{F}}_{\mathrm{BA}}=\text {बल पर } \mathrm{B} \text { के कारण } \mathrm{A} $

2. गति के दूसरे नियम से

$ F_x =\frac{dP_x}{dt}=ma_x \quad F_y =\frac{dP_y}{dt}=ma_y \quad F_y =\frac{dP_y}{dt}=ma_y $

5. तोलनयंत्र :

वजन मापने वाली मशीन वजन नहीं मापती बल्कि वस्तु द्वारा उसकी ऊपरी सतह पर लगाए गए बल को मापती है।

6. स्प्रिंग का बल $\overrightarrow{F}=-k \overrightarrow{x}$

x अपनी प्राकृतिक लंबाई से मुक्त सिरे का विस्थापन है या स्प्रिंग का विरूपण है $\mathrm{K}=$ वसंत निरंतर।

7. वसंत संपत्ति $\mathrm{K} \times \ell=$ स्थिर $=$ वसंत की प्राकृतिक लंबाई.

8. यदि स्प्रिंग को अनुपात में दो भागों में काटा जाए $m: n$ तो स्प्रिंग स्थिरांक द्वारा दिया जाता है

$ l_1 = \frac{ml}{m+n}; \quad l_2 = \frac{nl}{m+n}; \क्वाड k_l = k_1 l_1 = k_2 l_2 $

स्प्रिंग्स के श्रृंखला संयोजन के लिए

$ \frac{1}{k_{eq}}=\frac{1}

स्प्रिंग के समानांतर संयोजन के लिए

$ k_{\text {eq }}=k_{1}+k_{2}+k_{3} \ldots \ldots \ldots \ldots $

9. कमानीदार तराज़ू:

इससे वजन नहीं मापा जाता. यह हुक पर वस्तु द्वारा लगाए गए बल को मापता है।

याद करना :

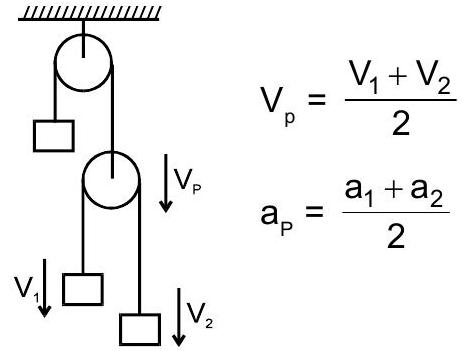
11। $$ a = \frac{(m_2 - m_1)g}{m_1 + m_2} $$ $$ टी = \frac{2m_1m_2g}{m_1+m_2} $$

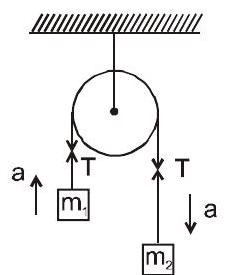
12. वेज बाधा:

यदि कोई विकृति नहीं है और वे संपर्क में रहते हैं तो दो वस्तुओं के संपर्क तल की लंबवत दिशा में वेग के घटक हमेशा बराबर होते हैं।

13. एक प्रणाली के लिए न्यूटन का नियम

$ \ओवरराइटएरो{F_{ext}} = m_1\ओवरराइटएरो{a_1} + m_2\ओवरराइटएरो{a_2} + m_3\ओवरराइटएरो{a_3} + \ldots $

$ \overrightarrow{\mathrm{F}}_{\mathrm{ext}}=$ सिस्टम पर शुद्ध बाहरी बल।

$ m_1, m_2, m_3$ का द्रव्यमान है सिस्टम की वस्तुएं और

$ \overrighterror{a_1},\overrightarrow{a_2}, \overrightarrow{a_3} $ का त्वरण है क्रमशः वस्तुएं

14. गैर जड़त्वीय फ्रेम के लिए न्यूटन का नियम:

$\overrightarrow{F_{Real}} + \overrightarrow{F_{Pseudo}} = m\overrightarrow{a}$

परिणामी बल में वास्तविक और छद्म बल का शुद्ध योग लिया जाता है।

$ \vec{a}= $ कण का त्वरण गैर जड़त्वीय फ्रेम में

$ \overrightarrow{F_{Pseudo}} = -m \overrightarrow{a} $

(ए) जड़त्वीय संदर्भ फ्रेम: संदर्भ का फ्रेम निरंतर वेग के साथ घूम रहा है।

(बी) गैर-जड़त्वीय संदर्भ फ्रेम: गैर-शून्य त्वरण के साथ चलने वाला संदर्भ फ्रेम।

टकराव

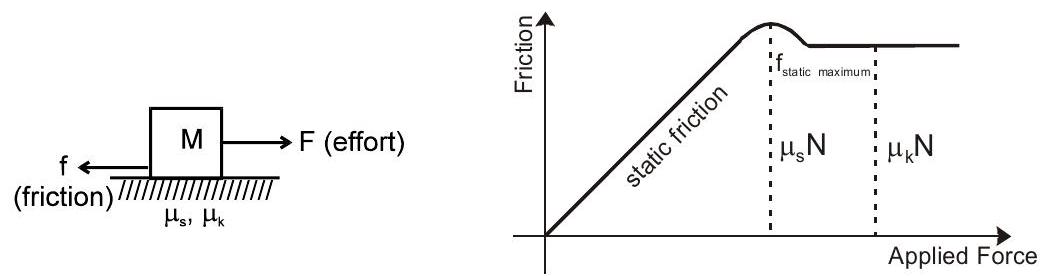
घर्षण बल दो प्रकार का होता है। (ए) काइनेटिक (बी) स्थिर

काइनेटिक घर्षण: $f_{k}=\mu_{k} N$

आनुपातिकता स्थिरांक $\mu_{\mathrm{k}}$ इसे गतिज घर्षण का गुणांक कहा जाता है और इसका मान संपर्क में आने वाली दो सतहों की प्रकृति पर निर्भर करता है।

स्थैतिक घर्षण :

यह दो सतहों के बीच तब मौजूद होता है जब सापेक्ष गति की प्रवृत्ति होती है लेकिन दो संपर्क सतहों पर कोई सापेक्ष गति नहीं होती है।

इसका मतलब है कि स्थैतिक घर्षण एक परिवर्तनशील और स्व-समायोजन बल है। हालाँकि इसका एक अधिकतम मान होता है जिसे सीमित घर्षण कहा जाता है।

$ f_{\max }=\mu_{s} N $

$ 0 \leq f_{s} \leq f_{s \max } $

कार्य_शक्ति_और_ऊर्जा

निरंतर बल द्वारा किया गया कार्य:

$ गणितबीएफ $

कई बलों द्वारा किया गया कार्य

$ \Sigma \vec{F}=\vec{F_1}+\vec{F_2}+\vec{F_3}+\ldots \ldots $

$ W=[\Sigma \vec{F}] \cdot \vec{S} …(i)$

$ W=\vec{F_1} \cdot \vec{S}+\vec{F_2} \cdot \vec{S}+\vec{F_3} \cdot \vec{S}+\ldots \ldots $

$ W=W_{1}+W_{2}+W_{3}+\ldots \ldots \ldots . . . . . $

या

परिवर्तनशील बल द्वारा किया गया कार्य

$ \mathrm{dW}=\overrighterror{\mathbf{F}} \cdot \mathbf{d} \overrightarrow{\mathbf{s}} $

संवेग और गतिज ऊर्जा के बीच संबंध

$$ \mathrm{K}=\frac{\mathrm{p}^{2}}{2 \mathrm{~m}} \text { और } \mathrm{P}=\sqrt{2 \mathrm{mK}} ; \mathrm{P}=\text {रैखिक संवेग } $$

संभावित ऊर्जा

$\int_{U_{1}}^{U_{2}} d U=-\int_{r_{1}}^{r_{2}} \vec{F} \cdot d \vec{r} \quad \text { i.e., } $

$U_{2}-U_{1}=-\int_{r_{1}}^{r_{2}} \vec{F} \cdot d \vec{r}=-W$

$U=-\int_{\infty}^{r} \vec{F} \cdot d \vec{r}=-W $ $$

रूढ़िवादी ताकतें

$$ \mathrm{F}=-\frac{\आंशिक \mathrm{U}}{\आंशिक \mathrm{r}} $$

कार्य-ऊर्जा प्रमेय

$$ W_{C}+W_NC+W_PS=\Delta K $$

कार्य-ऊर्जा प्रमेय का संशोधित रूप

$ W_{C}=-\Delta U $

$ W_{NC}+W_{PS}=\Delta K+\Delta U $

$ W_{NC}+W_{PS}=\Delta E $

शक्ति

औसत शक्ति ( $\bar{P}$ या $p_{a v}$ ) एक एजेंट द्वारा वितरित किया जाता है $\bar{P}$ या

$p_{a v}=\frac{W}{t}$

$$ P=\frac{\vec{F} \cdot d \vec{S}}{dt}=\vec{F} \cdot \frac{d \vec{S}}{dt}=\vec{F} \ cdot \vec{V} $$