गुरुत्वाकर्षण: गुरुत्वाकर्षण का सार्वभौमिक नियम

$ F \propto \frac{m_{1} m_{2}}{r^{2} $

कहाँ $\mathrm{G}=6.67 \times 10^{-11} \mathrm{Nm}^{2} \mathrm{~kg}^{-2}$ सार्वभौमिक गुरुत्वाकर्षण स्थिरांक है.

न्यूटन का गुरुत्वाकर्षण का नियम वेक्टर रूप में:

$ \vec{F_{12}} = \frac{Gm_1m_2}{r^2} \quad \hat{r} \quad $ & $ \vec{F_{21}} = \frac{Gm_1m_2}{r^2} $

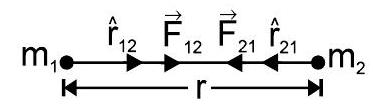अब $\hat{r_{12}} = -\hat{r_{21}}$, इस प्रकार

$\vec{F_{21}}=\frac{-G m_1 m_2}{r^2} \hat{r}_{12}$.

ऊपर की तुलना करने पर, हमें मिलता है $\vec{F_{12}}=-\vec{F_{21}}$

गुरुत्वाकर्षण क्षेत्र $\quad E=\frac{F}{m}=\frac{G M}{r^{2}}$

**गुरुत्वाकर्षण क्षमता:**गुरुत्वाकर्षण क्षमता, $ V=-\frac{GM}{r} . \quad E=-\frac{d V}{dr} $

1. अँगूठी। $V=\frac{-G M}{x \text { or }\left(a^{2}+r^{2}\right)^{1 / 2}} \quad \quad E=\frac{-G M r}{\left(a^{2}+r^{2}\right)^{3 / 2}} \hat{r}$

$ \text { या } E=-\frac{GM \cos \theta}{x^{2}} $

दूरी पर गुरुत्वाकर्षण क्षेत्र अधिकतम होता है,

$ r= \pm a / \sqrt{2} \text { और यह }-2 GM / 3 \sqrt{3} a^{2} है $

2. पतली गोलाकार डिस्क.

$V=\frac{-2 G M}{a^{2}}\left[\left[a^{2}+r^{2}\right]^{\frac{1}{2}}-r\right] E=-\frac{2 G M}{a^{2}}\left[1-\frac{r}{\left[r^{2}+a^{2}\right]^{\frac{1}{2}}}\right]=-\frac{2 G M}{a^{2}}[1-\cos \theta]$

3. गैर संवाहक ठोस क्षेत्र

(ए) गोले के अंदर बिंदु पी। $r \leq a$, तब

$V=-\frac{G M}{2 a^{3}}\left(3 a^{2}-r^{2}\right) E=-\frac{G M r}{a^{3}}$, और केंद्र में $V=-\frac{3 G M}{2 a}$ और $E=0$

(बी) प्वाइंट $P$ क्षेत्र के बाहर.

$r \geq a$, तब $\quad V=-\frac{G M}{r} \quad \quad E=-\frac{G M}{r^{2}}$

4. एकसमान पतला गोलाकार खोल/संवाहक ठोस गोला

(एक बिंदु $P$ खोल के अंदर.

$r \leq a$, तब $V=\frac{-G M}{a} \quad E=0$

(बी) बिंदु $P$ बाहरी आवरण.

$r \geq a$, तब $V=\frac{-G M}{r} \quad E=-\frac{G M}{r^{2}}$

गुरुत्वाकर्षण के कारण त्वरण में भिन्नता:

1. ऊंचाई का प्रभाव

$ g_{h}=\frac{G M_{e}}} \दाएं)^{-2} $ $ \simeq g\left(1-\frac{2 h}{R_{e}}\right) \text {कब } h < $

2. गहराई का प्रभाव $g_{d}=g\left(1-\frac{d}{R_{e}}\right)$

3. पृथ्वी की सतह का प्रभाव

भूमध्यरेखीय त्रिज्या लगभग है $21 \mathrm{~km}$ इसकी ध्रुवीय त्रिज्या से अधिक लंबा। हम जानते हैं, $g=\frac{GM_{e}}{R_{e}^{2}}$ इस तरह $g_{\text {pole }}>g_{\text {equator }}$.

उपग्रह वेग (या कक्षीय वेग)

$ v_{0}=\left[\frac{G M_{e}}{\left(R_{e}+h\right)}\right]^{\frac{1}{2}}=\left[\ frac{g R_{e}^{2}}{\left(R_{e}+h\right)}\right]^{\frac{1}{2}} $

कब $h«R_e$ तब $v_0=\sqrt{gR}$

$ \इसलिए \quad v_{0}=\sqrt{9.8 \times 6.4 \times 10^{6}} $ $ =7.92 \times 10^{3} \mathrm{ms}^{-1}=7.92 \mathrm{km} \mathrm{s}^{1} $

सैटेलाइट की समयावधि $ T=\frac{2 \pi\left(R_{e}+h\right)}{\left[\frac{g R_{e}^{2}}{\left(R_{e}+h\right) > {3}}{g}\दाएं]^{\frac{1}{2}} $

उपग्रह की ऊर्जा $U=\frac{-G M_{e} m}{r} \quad$ के.ई $=\frac{G M_{e} m}{2 r} ;$ फिर कुल ऊर्जा $\rightarrow E=-\frac{G M_{e} m}{2 R_{e}}$

केप्लर के नियम

क्षेत्र का कानून: सूर्य और ग्रह को मिलाने वाली रेखा समय के समान अंतराल में समान क्षेत्रों को पार करती है।

क्षेत्रीय वेग $=\frac{\text { area swept }}{\text { time }}=\frac{\frac{1}{2} r(r d \theta)}{d t}=7 \frac{1}{2} r^{2} \frac{d \theta}{d t}=$ स्थिर ।

इस तरह $\frac{1}{2} r^{2} \omega=$ स्थिर।

अवधि का नियम: $\frac{T^{2}}{R^{3}}=$ स्थिर