1. प्रकाश का परावर्तन

(बी) $\angle \mathrm{i}=\angle \mathrm{r}$

1.3 समतल दर्पण द्वारा परावर्तन के कारण छवि के लक्षण:

(ए) दर्पण से वस्तु की दूरी $=$ दर्पण से छवि की दूरी.

(बी) एक बिंदु वस्तु और उसकी छवि को जोड़ने वाली रेखा परावर्तक सतह के लंबवत होती है।

(सी) छवि का आकार वस्तु के समान है।

(डी) किसी वास्तविक वस्तु के लिए छवि आभासी होती है और आभासी वस्तु के लिए छवि वास्तविक होती है

2. वस्तु और छवि के वेग के बीच संबंध:

दर्पण संपत्ति से: $x_{i m}=-x_{o m}, y_{i m}=y_{o m}$ और $z_{i m}=z_{o m}$ यहाँ $x_{\text {im }}$ मतलब ’ $x$ ’ दर्पण के संबंध में छवि का समन्वय।

इसी प्रकार दूसरों का भी अर्थ होता है।

wrt समय को विभेदित करने पर, हमें प्राप्त होता है

3. गोलाकार दर्पण

$\frac{1}{v}+\frac{1}{u}=\frac{2}{R}=\frac{1}{f}\hspace{10mm}…Mirror formula$

$\mathrm{x}$ अवतल दर्पण के वक्रता केंद्र और फोकस का समन्वय ऋणात्मक होता है और उत्तल दर्पण का समन्वय धनात्मक होता है। दर्पण के मामले में चूँकि प्रकाश किरणें वापस परावर्तित होती हैं - $X$ दिशा, अत: -ve का चिह्न $v$ वास्तविक छवि और +ve चिह्न को इंगित करता है $v$ आभासी छवि को इंगित करता है

(बी) पार्श्व आवर्धन (या अनुप्रस्थ आवर्धन)

(डी) अंतर करने पर (ए) हमें मिलता है $\frac{d v}{d u}=-\frac{v^{2}}{u^{2}}$.

(ई) समय के संबंध में (ए) अंतर करने पर हमें प्राप्त होता है $\frac{\mathrm{dv}}{\mathrm{dt}}=-\frac{\mathrm{v}^{2}}{\mathrm{u}^{2}} \frac{\mathrm{du}}{\mathrm{dt}}$, कहाँ $\frac{\mathrm{dv}}{\mathrm{dt}}$ मुख्य अक्ष के अनुदिश छवि का वेग है $\frac{\mathrm{du}}{\mathrm{dt}}$ मुख्य अक्ष के अनुदिश वस्तु का वेग है। नकारात्मक संकेत का तात्पर्य है कि ** दर्पण के मामले में, छवि हमेशा वस्तु की विपरीत दिशा में चलती है। यह चर्चा दर्पण के संबंध में और वस्तु के वेग के लिए है $x$ एक्सिस।**

(च) न्यूटन का सूत्र: $X Y=f^{2}$

$X$ और $Y$ मुख्य फोकस से क्रमशः वस्तु और छवि की दूरियाँ (मुख्य अक्ष के अनुदिश) हैं। इस सूत्र का उपयोग तब किया जा सकता है जब फोकस से दूरियों का उल्लेख किया जाता है या पूछा जाता है।

(जी) दर्पण की ऑप्टिकल शक्ति (डायोप्टर में) $=\frac{1}{f}$ $f=$ फोकल लंबाई चिन्ह सहित और मीटर में।

(ज) यदि मुख्य अक्ष के अनुदिश पड़ी वस्तु बहुत छोटे आकार की नहीं है, तो अनुदैर्ध्य आवर्धन $=\frac{v_2-v_1}{u_2-u_1}$ (यह सदैव उल्टा रहेगा)

4. प्रकाश का अपवर्तन

वैक्यूम। $\mu=\frac{\text { speed of light in vacuum }}{\text { speed of light in medium }}=\frac{\mathrm{c}}{\mathrm{V}}$.

4.1 अपवर्तन के नियम (किसी भी अपवर्तक सतह पर)

(बी) $\quad \frac{\operatorname{Sini}}{\operatorname{Sin} r}=$ मीडिया के किसी भी जोड़े के लिए और दी गई तरंग लंबाई के प्रकाश के लिए स्थिरांक। इसे स्नेल के नियम के नाम से जाना जाता है। ज्यादा ठीक,

$ \frac{\sin i}{\sin r}=\frac{n_2}{n_1}=\frac{v_1}{v_2}=\frac{\lambda_{1}}{\lambda_{2}} $

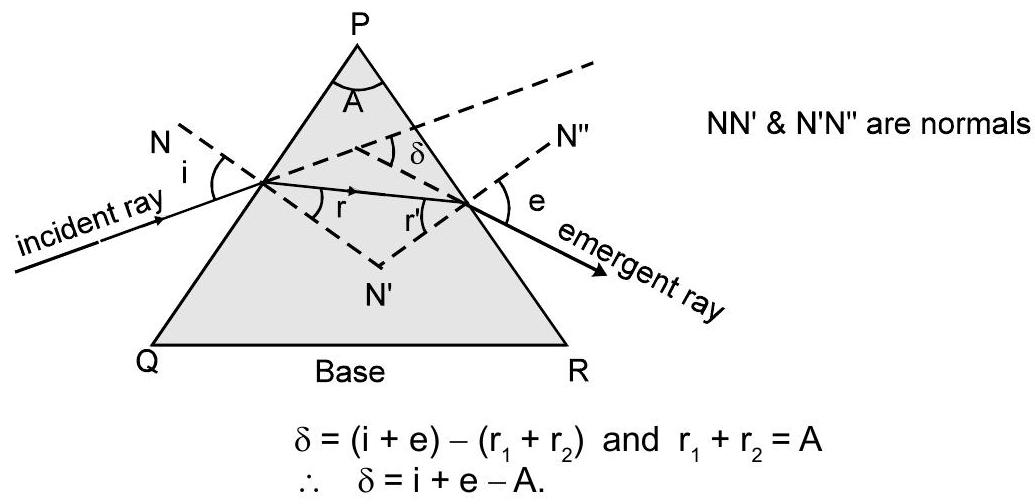
4.2 अपवर्तन के कारण किरण का विचलन

विचलन $(\delta)$ पर किरण घटना का $\angle \mathrm{i}$ और पर अपवर्तित हो गया $\angle \mathrm{r}$ द्वारा दिया गया है $\delta=|\mathrm{i}-\mathrm{r}|$.

5. प्रकाश किरणों की उत्क्रमणीयता का सिद्धांत

परावर्तित किरण के पथ पर चलने वाली किरण आपतित किरण के पथ पर परावर्तित होती है। एक अपवर्तित किरण अपने पथ के साथ वापस यात्रा करने के लिए आपतित किरण के पथ के साथ अपवर्तित हो जाएगी। इस प्रकार आपतित एवं अपवर्तित किरणें परस्पर प्रतिवर्ती होती हैं।

7. जलमग्न वस्तु की स्पष्ट गहराई और बदलाव

लगभग सामान्य घटना पर (आपतन का छोटा कोण i) स्पष्ट गहराई ( $\mathrm{d}^{\prime}$ ) द्वारा दिया गया है:

${d}^{\prime} = \frac{d}{n_\text{relative}} = \frac{n_i(R.I. \text{of medium of incidence})}{n_r(R.I. \text{of medium of refraction})}$

स्पष्ट बदलाव $=d\left(1-\frac{1}{n_{\text {rel }}}\right)$

एक समग्र स्लैब के माध्यम से अपवर्तन (या कई समानांतर मीडिया के माध्यम से अपवर्तन, जैसा कि आरआई के माध्यम से देखा जाता है $\mathrm{n}_{0}$ ) स्पष्ट गहराई (अंतिम सतह से अंतिम छवि की दूरी)

$=\frac{t_1}{n_{1rel}}+\frac{t_2}{n_{2rel}}+….+\frac{t_n}{n_{n_rel}}$

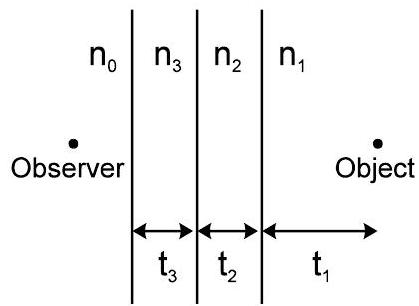
स्पष्ट बदलाव $=t_{1}\left[1-\frac{1}{n_{1 \text { rel }}}\right]+t_{2}\left[1-\frac{1}{n_{2 \text { rel }}}\right]+\ldots \ldots . .+\left[1-\frac{n}{n_{n \text { rel }}}\right]$

8. क्रांतिक कोण और पूर्ण आंतरिक परावर्तन (टीआईआर)

$C=\sin ^{-1} \frac{n_{r}}{n_{d}}$

(i) टीआईआर की शर्तें

(ए) प्रकाश सघन माध्यम से इंटरफ़ेस पर आपतित होता है।

(बी) आपतन कोण क्रांतिक कोण से अधिक होना चाहिए ( $\mathrm{i}>\mathrm{c})$.

9. प्रिज्म द्वारा अपवर्तन

9.1 प्रिज्म के लक्षण

9.2 की विविधता $\delta$ बनाम $i$

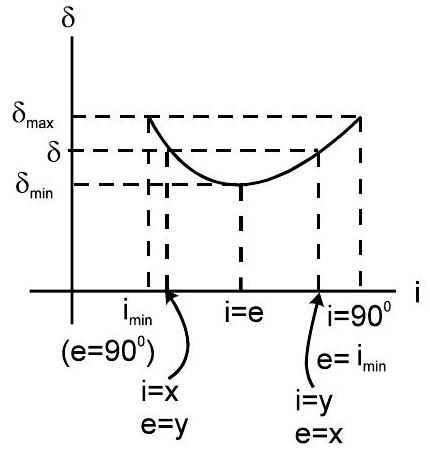
(1) आपतन का एक और केवल एक कोण है जिसके लिए विचलन का कोण न्यूनतम है।

(2) कब $\delta=\delta_{\min }$, तो न्यूनतम विचलन का कोण $\mathrm{i}=\mathrm{e}$ और $r_{1}=r_{2}$, किरण अपवर्तक सतहों से सममित रूप से गुजरती है। हम सरल गणना द्वारा यह दिखा सकते हैं $\delta_{\min }=2i_{min}-A$ कहाँ $\mathrm{i}_{\min }=$ न्यूनतम विचलन के लिए आपतन कोण और $r=A / 2$.

$n_{rel}=\frac{sin [\frac{A+ \delta_m}{2}]}{sin[\frac{A}{2}]}$ , कहाँ $n_{rel}=\frac{n_{prism}}{n_{surroundings}}$

भी $\quad \delta_{\min }=(n-1) A($ के छोटे मूल्यों के लिए $\angle A)$

(3) पतले प्रिज्म के लिए $\left(\mathrm{A} \leq 10^{\circ}\right)$ और के छोटे मूल्य के लिए $i$, के सभी मान

$ \delta = (n_{rel} - 1 ) A $ $ \quad where $ $ n_{rel} = \frac{n_{prims}}{n_{surrounding}} $

10. प्रकाश का प्रकीर्णन

श्वेत प्रकाश की किरण का कई घटकों में कोणीय रूप से विभाजित होना तथा विभिन्न दिशाओं में फैलना प्रकाश का विक्षेपण कहलाता है। यह घटना इसलिए है क्योंकि विभिन्न तरंग दैर्ध्य की तरंगें निर्वात में समान गति से चलती हैं लेकिन एक माध्यम में अलग-अलग गति से चलती हैं।

किसी माध्यम का अपवर्तनांक तरंगदैर्घ्य पर भी थोड़ा निर्भर करता है। तरंग दैर्ध्य के साथ अपवर्तक सूचकांक की यह भिन्नता कॉची के सूत्र द्वारा दी गई है।

कॉची का सूत्र $n(\lambda)=a+\frac{b}{\lambda^{2}}$ कहाँ $a$ और $b$ किसी माध्यम के धनात्मक स्थिरांक हैं।

अपवर्तित (बिखरे हुए) प्रकाश में अत्यधिक रंगों की किरणों के बीच के कोण को विक्षेपण कोण कहा जाता है।

छोटे ‘ए’ और छोटे ‘ए’ के प्रिज्म के लिए $i$ ’ :

$\theta=(n_v-n_r)A$

किरण का विचलन (जिसे माध्य विचलन भी कहा जाता है)

$\delta=\delta_{\mathrm{y}}=\left(\mathrm{n}_{\mathrm{y}}-1\right) \mathrm{A}$

फैलाने वाली शक्ति $(\omega)$ प्रिज्म की सामग्री का माध्यम निम्न द्वारा दिया गया है:

$\omega=\frac{n_v-n_r}{n_y-1}$

छोटे कोण वाले प्रिज्म के लिए $\left(A \leq 10^{\circ}\right)$ छोटे कोण पर प्रकाश आपतित होने के साथ $i$ :

$\frac{n_v-n_r}{n_y-1}=\frac{\delta_v-\delta_r}{\delta_y}=\frac\theta{\delta_y}$

$=\frac{\text { angular dispersion }}{\text { deviation of mean ray (yellow) }}$

[ $n_{y}=\frac{n_{v}+n_{r}}{2}$ अगर $n_{y}$ समस्या में नहीं दिया गया है]

$\omega=\frac{\delta_{v}-\delta_{r}}{\delta_{y}}=\frac{n_{v}-n_{r}}{n_{y}-1}$ [लेना $n_{y}=\frac{n_{v}+n_{r}}{2}$ यदि का मान $n_{y}$ समस्या में नहीं दिया गया है]

$n_{v}, n_{r}$ और $n_{y}$ हैं $R$. I. क्रमशः बैंगनी, लाल और पीले रंगों के लिए सामग्री का।

11। दो प्रिज्मों का संयोजन

कोणीय फैलाव और विचलन के विभिन्न संयोजन प्राप्त करने के लिए दो या दो से अधिक प्रिज्मों को विभिन्न तरीकों से जोड़ा जा सकता है।

(ए) प्रत्यक्ष दृष्टि संयोजन (विचलन के बिना फैलाव) प्रत्यक्ष दृष्टि संयोजन की शर्त है:

$\left[\frac{n_{v}+n_{r}}{2}-1\right] A=\left[\frac{n_{v}^{\prime}+n_{r}^{\prime}}{2}-1\right] A^{\prime}$ $\Leftrightarrow\left[n_{y}-1\right] A=\left[n_{y}^{\prime}-1\right] A^{\prime}$

(बी) अक्रोमैटिक संयोजन (बिना फैलाव के विचलन।)

अक्रोमेटिक संयोजन के लिए शर्त है: $\left(n_{v}-n_{r}\right) A=\left(n_{v}^{\prime}-n_{r}^{\prime}\right) A^{\prime}$

12. गोलाकार सतहों पर अपवर्तन

दो मीडिया को अलग करने वाली गोलाकार सतह पर आपतित पैराएक्सियल किरणों के लिए:

$\frac{n_2}{V}-\frac{n_1}{u}=\frac{n_2-n_1}{R}$

जहां प्रकाश अपवर्तक सूचकांक के माध्यम से चलता है $n_{1}$ अपवर्तक सूचकांक के माध्यम के लिए $n_{2}$.

अनुप्रस्थ आवर्धन $(\mathrm{m}$ ) (प्रमुख अक्ष के लंबवत आयाम का)

गोलाकार सतह पर अपवर्तन के कारण दिया जाता है

$m=\frac{v-R}{u-R}=\left(\frac{v / n_{2}}{u / n_{1}}\right)$

13. गोलाकार पतले लेंस पर अपवर्तन

एक पतला लेंस उत्तल कहलाता है यदि यह बीच में मोटा हो और यदि यह सिरों पर मोटा हो तो इसे अवतल कहा जाता है।

एक गोलाकार, पतले लेंस के लिए जिसके दोनों तरफ समान माध्यम हो:

$ \frac{1}{V}-\frac{1}{u}=(n_{rel}{-1})(\frac{1}{R1}-\frac{1}{R2}) \hspace{ 1मिमी}जहां \hspace{1मिमी} n_{rel}=\frac{n_{लेंस}}{n_{मध्यम}} $

$\frac {1}{f}=(n_{rel}-1)(\frac{1}{R_1}-\frac{1}{R2})$

$\frac{1}{v}-\frac{1}{u}=\frac{1}{v} \rightarrow $ लेंस निर्माता का सूत्र

$m=\frac{v}{u}$

लेंस का संयोजन: $\quad \frac{1}{F}=\frac{1}{f_{1}}+\frac{1}{f_{2}}+\frac{1}{f_{3}} \ldots$

ऑप्टिकल उपकरण

सरल माइक्रोस्कोप

• आवर्धन शक्ति : $\frac{\mathrm{D}}{\mathrm{U}_{0}}$

• जब प्रतिबिम्ब अनन्त पर बनता है $M_{\infty}=\frac{D}{f}$

• जब प्रिंट के निकट परिवर्तन बनता है $D . M_{D}=1+\frac{D}{f}$

यौगिक सूक्ष्मदर्शी

$ \शुरुआत{सरणी}{} \text{आवर्धक शक्ति} & और \text{माइक्रोस्कोप की लंबाई}\\ \\ M=\frac{V_{0}D_{0}}{U_0{U_e}} & & L=V_o+U_e \\ \\ M_{\infty}=\frac{V_{0} D} \\ M_{D}=\frac{V_{0}}{U_{0}}\left(1+\frac{D}{f_{e}}\right) & & L_{D}=V_{0}+ \frac{D \cdot f_{e}}{D+f_{e}} \अंत{सरणी} $

खगोलीय टेलीस्कोप

$ \शुरुआत{सरणी}{} \text{आवर्धक शक्ति} & और \text{माइक्रोस्कोप की लंबाई}\\ \\ M=\frac{f_o}{\mu_e} & & L=f+u_{e} \\ \\ M_{\infty}=\frac{f_{0}}{f_{e}} & L=f_{0}+f_{e}\\ \\ M_{D}=\frac{f_{0}}{f_{e}}\left(1+\frac{f_{e}}{D}\right) & & L_{D}=f_{0}+ \frac{D f_{e}}{D+f_{e}} \अंत{सरणी} $

स्थलीय टेलीस्कोप

$ \शुरुआत{सरणी}{} \text{आवर्धक शक्ति} & और \text{माइक्रोस्कोप की लंबाई}\\ \\ M=\frac{f_0}{U_e} & & L=f_{0}+4 f+U_{e} \\ \\ M_{\infty}=\frac{f_{0}}{f_{e}} & L=f_{0}+4 f+f_{e}\\ \\ M_{D}=\frac{f_{0}}{f_{e}}\left(1+\frac{f_{e}}{D}\right) & & L_{D}=f_{0}+ 4 f+\frac{D f_{e}}{D+f_{e}} \अंत{सरणी} $

गैलीलियन टेलीस्कोप

$ \शुरुआत{सरणी}{} \text{आवर्धक शक्ति} & और \text{माइक्रोस्कोप की लंबाई}\\ \\ M=\frac{f_{0}}{U_{e}} और L=f_{0}-U_{e} \\ \\ M_{\infty}=\frac{f_{0}}{f_{e}} & & L=f_0-f_e\\ \\ M _ \frac{f_{e} D}{D-f_{e}} \अंत{सरणी} $

सुलझाने की शक्ति

माइक्रोस्कोप $\mathrm{R}=\frac{1}{\Delta \mathrm{d}}=\frac{2 \mu \sin \theta}{\lambda}$

दूरबीन. $\mathrm{R}=\frac{1}{\Delta \theta}=\frac{\mathrm{a}}{1.22 \lambda}$