तरल पदार्थ, सतह का तनाव, चिपचिपापन और लोच:

1. हाइड्रोलिक प्रेस. $ p=\frac{f}{a}=\frac{F}{A} \text { या } F=\frac{A}{a} \times f $ हाइड्रोस्टेटिक विरोधाभास $P_{A}=P_{B}=P_{C}$

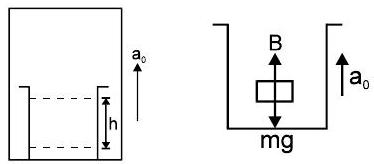
(i) लिफ्ट में रखा तरल पदार्थ: जब लिफ्ट त्वरण के साथ ऊपर की ओर बढ़ती है $a_{0}$ फिर द्रव में दबाव, गहराई पर ’ $h$ ’ द्वारा दिया जा सकता है,

$$ p=\rho h\left[g+a_{0}\right] $$ और उछाल का बल, $B=m\left(g+a_{0}\right)$

(ii) क्षैतिज त्वरण में द्रव की मुक्त सतह : $ \tan \theta=\frac{a_{0}}{g} $

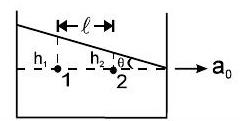$p_{1}-p_{2}=\rho \ell a_{0} \quad$ कहाँ $p_{1}$ और $p_{2}$ बिंदु 1 और 2 पर दबाव हैं।

तब $h_1-h_2=\frac{\ell a_0}{g}$

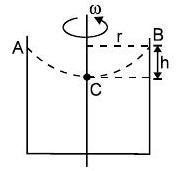
(iii) घूमते सिलेंडर की स्थिति में तरल की मुक्त सतह। $h=\frac{v^{2}}{2 g}=\frac{\omega^{2} r^{2}}{2 g}$

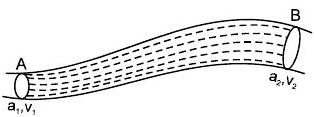
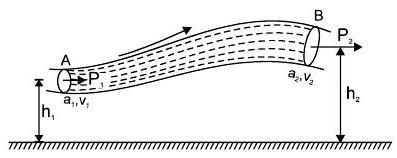
निरंतरता का समीकरण $a_{1} v_{1}=a_{2} v_{2}$ सामान्य तौर पर ए.वी $=$ स्थिर ।

बर्नौली का प्रमेय अर्थात $\frac{P}{\rho}+\frac{1}{2} v^{2}+g h=$ स्थिर।

(vi) टोरिसेली प्रमेय - (प्रवाह की गति) $v=\sqrt{\frac{2 g h}{1-\frac{A_{2}^{2}}{A_{1}{ }^{2}}}}, A_{2}=$ छेद का क्षेत्र $\mathrm{A}_{1}=$ जहाज का क्षेत्र.

लोच और चिपचिपाहट: तनाव $=\frac{\text { restoringforce }}{\text { area of the body }}=\frac{\mathrm{F}}{\mathrm{A}}$

छानना, $\in=\frac{\text { change in configuration }}{\text { original configuration }}$

(i) अनुदैर्ध्य तनाव $=\frac{\Delta \mathrm{L}}{\mathrm{L}}$

(ii) $\epsilon_{\mathrm{v}}=$ मात्रा तनाव $=\frac{\Delta \mathrm{V}}{\mathrm{V}}$

(iii) कतरनी तनाव: $\tan \phi$ या $\phi=\frac{\mathrm{X}}{\ell}$

1. यंग का लोच मापांक $\mathrm{Y}=\frac{\mathrm{F} / \mathrm{A}}{\Delta \mathrm{L} / \mathrm{L}}=\frac{\mathrm{FL}}{\mathrm{A} \Delta \mathrm{L}}$

प्रति इकाई आयतन संभावित ऊर्जा $=\frac{1}{2}($ तनाव $\times \operatorname{strain})=\frac{1}{2}\left(\mathrm{Y} \times \operatorname{strain}^{2}\right)$

अंतर-परमाणु बल-स्थिरांक $\mathrm{k}=\mathrm{Yr}_{0}$.

न्यूटन का श्यानता का नियम, $ F \propto A \frac{dv}{dx} \text { या } F=-\eta A \frac{dv}{dx} $

स्टोक्स का नियम $F=6 \pi \eta r v . \quad$ टर्मिनल वेग $=\frac{2}{9} \frac{r^{2}(\rho-\sigma) g}{\eta}$

सतह तनाव

सतह तनाव $(T)=\frac{\text { Total force on either of the imaginary line }(F)}{\text { Length of the line }(\ell)}$;

$ \mathrm{T}=\mathrm{S}=\frac{\Delta \mathrm{W}}{\mathrm{A}} $

इस प्रकार, सतह तनाव संख्यात्मक रूप से सतह ऊर्जा या सतह क्षेत्र में प्रति इकाई वृद्धि के लिए किए गए कार्य के बराबर है।

एक बुलबुले के अंदर: $\quad\left(p-p_{a}\right)=\frac{4 T}{r}=p_{\text {excess }} ;$

बूंद के अंदर: $\quad\left(p-p_{a}\right)=\frac{2 T}{r}=p_{\text {excess }}$

तरल में हवा के बुलबुले के अंदर: $\left(p-p_{a}\right)=\frac{2 T}{r}=p_{\text {excess }}$

केशिका वृद्धि $\quad h=\frac{2 T \cos \theta}{r \rho g}$