चालू बिजली
1. विद्युत प्रवाह
$I_{av} = \frac{\Delta q}{\Delta t} \hspace{1mm} and \hspace{1mm} instantaneous \hspace{1mm} current$
$i = \operatorname{Lim}_{\Delta t \rightarrow 0} \frac{\Delta q}{\Delta t}=\frac{dq}{dt}$
2. एक कंडक्टर में विद्युत धारा
$\mathrm{I}=\mathrm{nAeV}$.
$v_{d}=\frac{\lambda}{\tau}$,
$v_{d}=\frac{\frac{1}{2}\left(\frac{e E}{m}\right) \tau^{2}}{\tau}=\frac{1}{2} \frac{e E}{m} \tau$,
$\mathrm{I}=\mathrm{neAV}_{\mathrm{d}}$
3.वर्तमान घनत्व
$\overrightarrow{\mathrm{J}}=\frac{\mathrm{dl}}{\mathrm{ds}} \overrightarrow{\mathrm{n}}$
4.विद्युत प्रतिरोध
$I=neAV_{d}=neA\left(\frac{eE}{2 ~m}\right) \tau=\left(\frac{ne^{2} \tau}{2 ~m}\right) AE$
$\mathrm{E}=\frac{\mathrm{V}}{\ell} \quad$ इसलिए $\mathrm{I}=\left(\frac{\mathrm{ne}^{2} \tau}{2 \mathrm{~m}}\right)\left(\frac{\mathrm{A}}{\ell}\right) \mathrm{V}=\left(\frac{\mathrm{A}}{\rho \ell}\right)$ $ \mathrm{V}=\mathrm{V} / \mathrm{R} \Rightarrow \mathrm{V}=\mathrm{IR}$
$\rho$ प्रतिरोधकता कहलाती है (इसे विशिष्ट प्रतिरोध भी कहते हैं) और $\rho=\frac{2 \mathrm{~m}}{\mathrm{ne}^{2} \tau}=\frac{1}{\sigma}, \sigma$ चालकता कहलाती है. इसलिए कंडक्टरों में करंट उसके सिरों पर लागू संभावित अंतर के समानुपाती होता है। यह ओम का नियम है।
इकाइयाँ:
$\mathrm{R} \rightarrow \operatorname{ohm}(\Omega), \quad \rho \rightarrow \operatorname{ohm}-\operatorname{meter}(\Omega-\mathrm{m})$
इसे सीमेंस भी कहा जाता है, $\sigma \rightarrow \Omega^{-1} \mathrm{~m}^{-1}$.
तापमान पर प्रतिरोध की निर्भरता:
$\mathrm{R}=\mathrm{R}_{0}(1+\alpha \theta)$.
प्रतिरोध में विद्युत धारा
$ I=\frac{V_{2}-V_{1}}{R} $
5. विद्युत शक्ति
$\mathbf{P}=\mathbf{V}$ मैं
ऊर्जा $=\int \mathrm{pdt}$
$\mathrm{P}=\mathrm{I}^{2} \mathrm{R}=\mathrm{VI}=\frac{\mathrm{V}^{2}}{\mathrm{R}}$.
$\mathrm{H}=\mathrm{VIt}=\mathrm{I}^{2} \mathrm{Rt}=\frac{\mathrm{V}^{2}}{\mathrm{R}} \mathrm{t}$
$\mathrm{H}=\mathrm{I}^{2} \mathrm{RT}$ जौल $=\frac{\mathrm{I}^{2} \mathrm{RT}}{4.2}$ कैलोरी
9. किरचॉफ के नियम
9.1 किरचॉफ का वर्तमान कानून (जंक्शन कानून)
$\Sigma I_{in}=\Sigma I_{\text {out }}$
9.2 किरचॉफ का वोल्टेज नियम (लूप नियम)
$\Sigma$ आईआर $+\Sigma$ ईएमएफ $=0$ “.
10.प्रतिरोधों का संयोजन:
श्रृंखला में प्रतिरोध:
$R=R_{1}+R_{2}+R_{3} …… +R_{n} \quad$ (इसका मतलब यह है $R_{\text {eq }}$ किसी भी अवरोधक से अधिक बड़ा है) और
$V=V_{1}+V_{2}+V_{3}+$ $+V_{n}$
$V_{1}=\frac{R_{1}}{R_{1}+R_{2}+\ldots \ldots \ldots+R_{n}} V ;$
$V_{2}=\frac{R_{2}}{R_{1}+R_{2}+\ldots \ldots \ldots+R_{n}} V$;
2. समानांतर में प्रतिरोध:
$ \frac{1}{R_{eq}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}} $
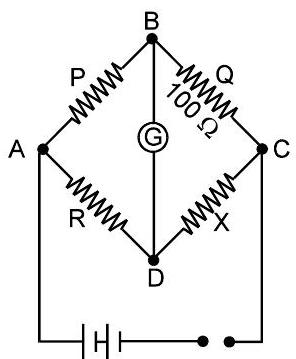
11। व्हीटस्टोन नेटवर्क : (4 टर्मिनल नेटवर्क)
$\quad $ $\quad $ $\quad $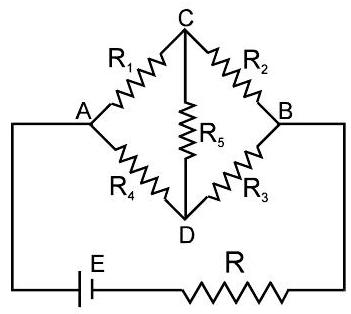
जब गैल्वेनोमीटर के माध्यम से धारा शून्य हो (शून्य बिंदु या संतुलन बिंदु) $\frac{P}{Q}=\frac{R}{S}$, तब $P S=Q R$
13. कोशिकाओं का समूहन
13.1श्रृंखला में कक्ष:

समकक्ष $EMFE_{eq}=E_{1}+E_{2}+\ldots \ldots .+E_{n}$ [लिखना $\mathrm{EMF}^{\prime}$ ध्रुवीयता के साथ]
समतुल्य आंतरिक प्रतिरोध $r_{\text {eq }}=r_{1}+r_{2}+r_{3}+r_{4}+\ldots .+r_{n}$
13.2समानांतर में कोशिकाएँ:
$E_{eq}=\frac{\varepsilon_{1} / r_{1}+\varepsilon_{2} / r_{2}+\ldots .+\varepsilon_{n} / r_{n}}{1 / r_{1}+1 / r_{2}+\ldots . .+1 / r_{n}}$ [ध्रुवीयता के साथ ईएमएफ का प्रयोग करें]
$\quad $ $\quad $ $\quad $
$\frac{1}{r_{\text {eq }}}=\frac{1}{r_{1}}+\frac{1}{r_{2}}+\ldots .+\frac{1}{r_{n}}$
15. एमीटर
इसे एमीटर में बदलने के लिए गैल्वेनोमीटर के साथ समानांतर में एक शंट (छोटा प्रतिरोध) जोड़ा जाता है। एक आदर्श एमीटर का प्रतिरोध शून्य होता है
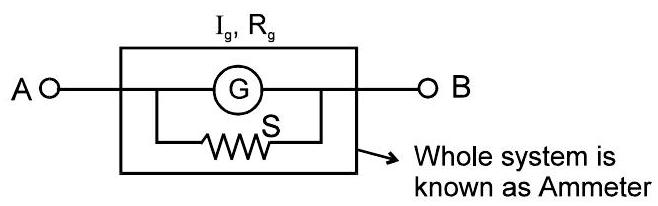
एमीटर को इस प्रकार दर्शाया जाता है -
यदि एमीटर द्वारा मापी जाने वाली धारा का अधिकतम मान I है तो $I_{G} \cdot R_{G}=\left(I-I_{G}\right) S$
$S=\frac{I_{G} \cdot R_{G}}{I-I_{G}} \quad S=\frac{I_{G} \times R_{G}}{I} \quad when \quad I \gg I_{G}$.
कहाँ $\quad I=$ अधिकतम धारा जिसे दिए गए एमीटर का उपयोग करके मापा जा सकता है।
16. वोल्टमीटर
गैल्वेनोमीटर के साथ श्रृंखला में एक उच्च प्रतिरोध रखा जाता है। इसका उपयोग किसी सर्किट में किसी प्रतिरोधक के बीच संभावित अंतर को मापने के लिए किया जाता है।
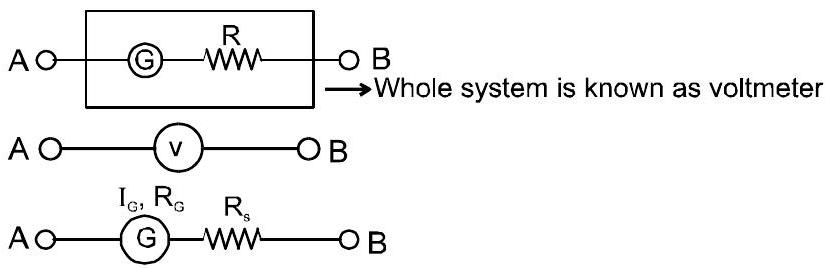
अधिकतम संभावित अंतर के लिए
$V = I_{G}.R_{S}+ I_{G}R_{G}$
$R_{S}=\frac{V}{I_{G}}-R_{G} \quad \text { if } $
$R_{G}«R_{S} \Rightarrow R_{S} \approx \frac{V}{I_{G}}$
17. पोटेंशियोमीटर
$\quad$ $\quad$ 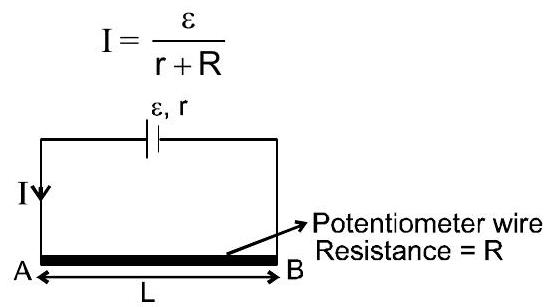
$V_{A}-V_{B}=\frac{\varepsilon}{R+r} \cdot R$
संभावित ढाल $(x) \rightarrow$ तार की प्रति इकाई लंबाई में संभावित अंतर
$ x=\frac{V_{A}-V_{B}}{L}=\frac{\varepsilon}{R+r} \cdot \frac{R}{L} $
पोटेंशियोमीटर का अनुप्रयोग
(ए)अज्ञात सेल का ईएमएफ ज्ञात करना और दो सेल के ईएमएफ की तुलना करना।
मेरे मामले में,
चित्र में (1) (2) से संयुक्त है तो लंबाई संतुलित करें $=\ell_{1} $
केस II में,
$ \varepsilon_{1}=x \ell_{1} \hspace{10mm}…(i) $
चित्र में (3) (2) से संयुक्त है तो लंबाई संतुलित करें $=\ell_{2}$
$\varepsilon_{2}=\mathrm{x} \ell_{2} \hspace{10mm}…(ii)$
$\frac{\varepsilon_{1}}{\varepsilon_{2}}=\frac{\ell_{1}}{\ell_{2}}$
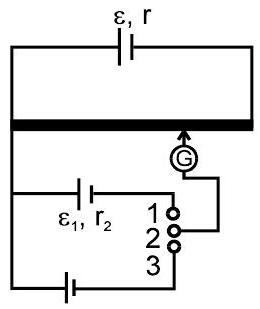 यदि इनमें से कोई एक $\varepsilon_{1}$ या $\varepsilon_{2}$ ज्ञात है अन्य को पाया जा सकता है। अगर $\mathrm{x}$ तब दोनों को जाना जाता है $\varepsilon_{1}$ और $\varepsilon_{2}$ पाया जा सकता है
यदि इनमें से कोई एक $\varepsilon_{1}$ या $\varepsilon_{2}$ ज्ञात है अन्य को पाया जा सकता है। अगर $\mathrm{x}$ तब दोनों को जाना जाता है $\varepsilon_{1}$ और $\varepsilon_{2}$ पाया जा सकता है
(बी) यदि प्रतिरोध ज्ञात है तो धारा ज्ञात करने के लिए
$V_{A}-V_{C}=x \ell_{1}$
$R_{1}=x\ell_{1}$
$I=\frac{x \ell_{1}}{R_{1}}$
$\quad$ $\quad$ 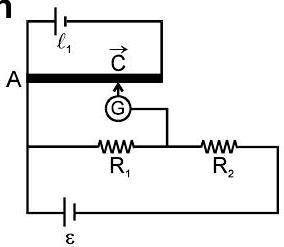
इसी प्रकार, हम का मूल्य ज्ञात कर सकते हैं $R_{2}$ भी।
पोटेंशियोमीटर आदर्श वोल्टमीटर है क्योंकि यह संतुलन बिंदु पर सर्किट से कोई विद्युत धारा नहीं खींचता है।
(सी) सेल का आंतरिक प्रतिरोध ज्ञात करने के लिए।
पहली व्यवस्था $\hspace{60mm}$ दूसरी व्यवस्था
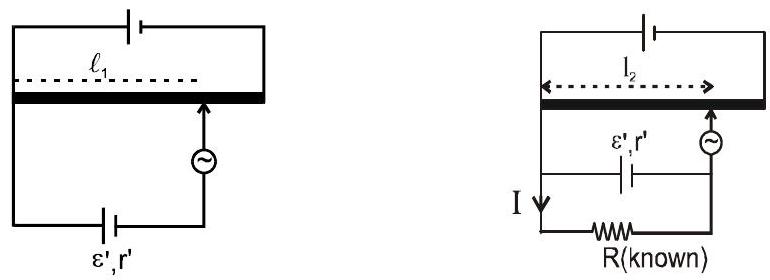
पहली व्यवस्था से $\quad \varepsilon^{\prime}=\mathrm{x} \ell_{1} \hspace{10mm}…(i)$
दूसरी व्यवस्था द्वारा $\mathrm{IR}=\mathrm{x} \ell_{2}$
$I=\frac{\mathrm{x} \ell_{2}}{R}, \quad \text { also } I=\frac{\varepsilon^{\prime}}{r^{\prime}+R}$
$\therefore \quad \frac{\varepsilon^{\prime}}{r^{\prime}+R} = \frac{xl_{2}}{R} \quad \Rightarrow \frac{xl_{1}}{r^{\prime}+R} = \frac{xl_{2}}{R}$
$=\left[\frac{\ell_{1}-\ell_{2}}{\ell_{2}}\right] R$
(डी) एमीटर और वोल्टमीटर को पोटेंशियोमीटर द्वारा स्नातक किया जा सकता है।
(ई) एमीटर और वोल्टमीटर को पोटेंशियोमीटर द्वारा कैलिब्रेट किया जा सकता है।
18. मीटर ब्रिज (अज्ञात प्रतिरोध मापने के लिए उपयोग)
अगर $A B=\ell \mathrm{cm}$, तब $B C=(100-\ell) \mathrm{cm}$.
के बीच तार का प्रतिरोध $A$ और $B, R \propto \ell$
[ $\because$ विशिष्ट प्रतिरोध $\rho$ और क्रॉस-सेक्शनल क्षेत्र A पूरे तार के लिए समान है]
$ \text { या } \quad R=\sigma \ell \hspace{10mm}…(i) $
कहाँ $\sigma$ प्रति प्रतिरोध है $\mathrm{cm}$ तार का.
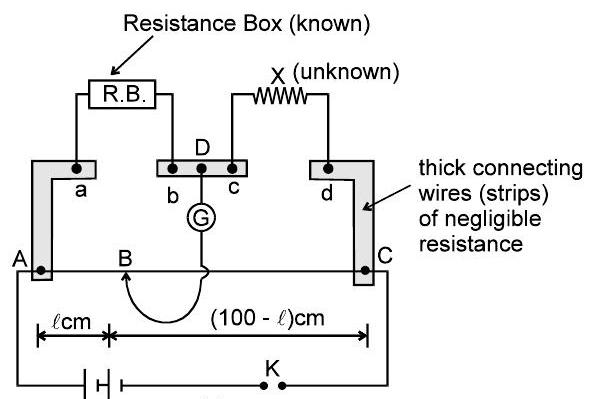
(ए)
(बी)
अगर $P$ के बीच तार का प्रतिरोध है $A$ और $B$ तब
$ P \propto \ell \Rightarrow \quad P=\sigma(\ell) $
इसी प्रकार, यदि $Q$ के बीच तार का प्रतिरोध है $B$ और $C$, तब
$ \शुरुआत{सरणी}{ll} एवं Q \propto 100-\ell \\ \इसलिए और Q=\sigma(100-\ell)\hspace{10mm}….(2) \अंत{सरणी} $
(1) को (2) से विभाजित करने पर, $\quad \frac{P}{Q}=\frac{\ell}{100-\ell}$
संतुलित व्हीटस्टोन ब्रिज के लिए शर्त लागू करने पर, हमें प्राप्त होता है $R Q=P X$
$$ \इसलिए \quad x=R \frac{Q}{P} \quad \text { या } \quad x=\frac{100-\ell}{\ell} R $$
तब से $\mathrm{R}$ और $\ell$ इसलिए, का मूल्य ज्ञात है $\mathrm{X}$ गणना की जा सकती है.





