1. औसत कोणीय वेग $\Rightarrow \quad \omega_{a v}=\frac{\theta_{2}-\theta_{1}}{t_{2}-t_{1}}=\frac{\Delta \theta}{\Delta t}$

2. तात्क्षणिक कोणीय वेग $\Rightarrow \omega=\frac{\mathrm{d} \theta}{\mathrm{dt}}$

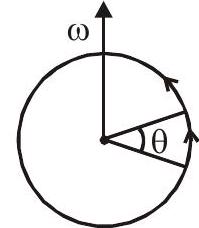
3. औसत कोणीय त्वरण

$\Rightarrow \quad \alpha_{a v}=\frac{\omega_{2}-\omega_{1}}{t_{2}-t_{1}}=\frac{\Delta \omega}{\Delta t}$

4. तात्क्षणिक कोणीय त्वरण $\Rightarrow \quad \alpha=\frac{\mathrm{d} \omega}{\mathrm{dt}}=\omega \frac{\mathrm{d} \omega}{\mathrm{d} \theta}$

5. गति और कोणीय वेग के बीच संबंध $\Rightarrow v=r \omega$ और $\vec{v}=\vec{\omega} \times \vec{r}$

6. स्पर्शरेखीय त्वरण (गति में परिवर्तन की दर)

$$ \दायाँ तीर \quad a_{t}=\frac{d V}{dt}=r \frac{d \omega}{dt}=\omega \frac{dr}{dt} $$

8. रेडियल या सामान्य या सेंट्रिपेटल त्वरण $\Rightarrow a_{r}=\frac{v^{2}}{r}=\omega^{2} r$

9. कुल त्वरण

$ \राइटएरो \vec{a}=\vec{a}_t+\vec{a}_r \राइटएरो a=\left(a_t^2+a_r^2\right)^{1 / 2} $

कहाँ $\vec{a}_t=\vec{\alpha} \times \vec{r}$ और $\vec{a}_r=\vec{\omega} \times \vec{v}$

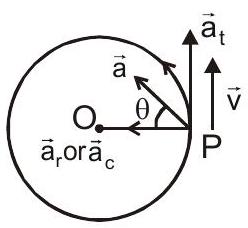
10. कोणीय त्वरण

$\Rightarrow \quad \vec{\alpha}=\frac{\mathrm{d} \vec{\omega}}{\mathrm{dt}}$ (असमान गोलाकार गति)

12. वक्रता त्रिज्या $R=\frac{v^{2}}{a_{\perp}}=\frac{m v^{2}}{F_{\perp}}$

अगर $y$ का एक कार्य है $x$.

अर्थात $y=f(x) \Rightarrow \quad R=\frac{\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{3 / 2}}{\frac{d^{2} y}{d x^{2}}}$

13. अवतल पुल पर सड़क की सामान्य प्रतिक्रिया

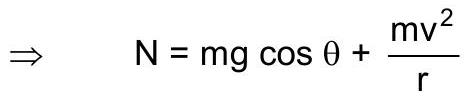
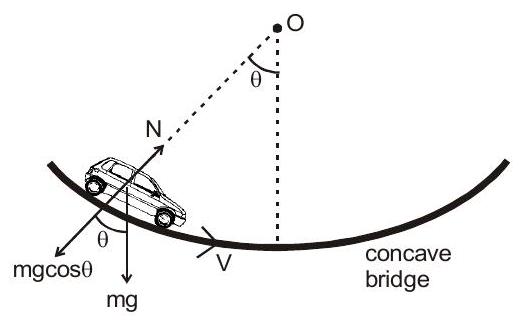
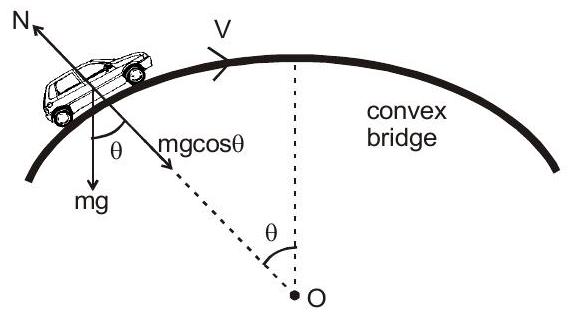
14. उत्तल पुल पर सामान्य प्रतिक्रिया

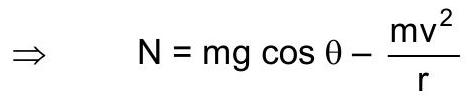
15. समतल सड़क पर वाहन का फिसलना

$\Rightarrow \quad \mathrm{v}_{\text {safe }} \leq \sqrt{\mu \mathrm{gr}}$

16. घूमते प्लेटफार्म पर किसी वस्तु का फिसलना

$\Rightarrow \quad \omega_{\max }=\sqrt{\mu \mathrm{g} / \mathrm{r}}$

17. साइकिल चालक का झुकना $\Rightarrow \tan \theta=\frac{v^{2}}{r g}$

18. बिना घर्षण के सड़क का किनारा $\Rightarrow \tan \theta=\frac{v^{2}}{\mathrm{rg}}$

19. घर्षण से सड़क का किनारा $\Rightarrow \frac{\mathrm{v}^{2}}{\mathrm{rg}}=\frac{\mu+\tan \theta}{1-\mu \tan \theta}$

20. किनारे वाली घर्षण वाली सड़क पर अधिकतम और न्यूनतम सुरक्षित गति

$$ V_{max}=\left[\frac{rg(\mu+\tan \theta)}{(1-\mu \tan \theta)}\right]^{1 / 2} $$ $$ V_{\min }=\left[\frac{rg(\tan \theta-\mu)}{(1+\mu \tan \theta)}\right]^{1 / 2} $$

21. केन्द्रापसारक बल (छद्म बल) $\Rightarrow f=m \omega^{2} r$, जब कण को एक फ्रेम के रूप में लिया जाता है तो वह बाहर की ओर कार्य करता है।

22. स्पष्ट वजन पर पृथ्वी के घूमने का प्रभाव $\Rightarrow \mathrm{N}=\mathrm{mg}-\mathrm{mR} \omega^{2} \cos ^{2} \theta$;

कहाँ $\theta \Rightarrow$ किसी स्थान पर अक्षांश

23. विभिन्न स्थितियों में एक ऊर्ध्वाधर लूप में एक गंभीर स्थिति के लिए विभिन्न मात्राएँ

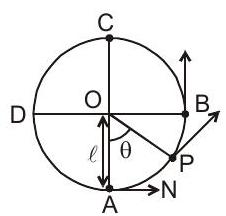
24. शंक्वाकार लोलक :

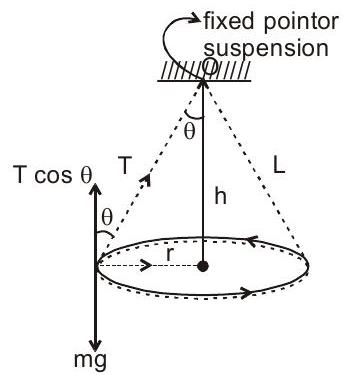
$$ \mathrm{T} \cos \theta=\mathrm{mg} $$ $$ T \sin \theta=m \omega^{2} r $$ $$ \इसलिए \quad \text {समयावधि }=\sqrt[2 \pi]{\frac{L \cos \theta}{g}} $$

25. कोणीय चरों के बीच संबंध :

$\omega_{0} \Rightarrow$ प्रारंभिक अंग. वेग $\quad \omega=\omega_{0}+\alpha t$

$\omega \Rightarrow \text{ Find angular velocity } \quad \theta=\omega_{0} t+\frac{1}{2} \alpha t^{2}$

$\omega \Rightarrow \text{Const. angular acceleration }\quad \omega^2 = \omega_0^2 + 2 \alpha \theta $

$\theta \Rightarrow$ कोणीय विस्थापन