सामूहिक क्षण: $\vec{M}=m \vec{r}$

‘एन’ असतत कणों की एक प्रणाली के द्रव्यमान का केंद्र

$$ \vec{r}_{cm} = \frac{m1\vec{r_1}+m_2\vec{r_2}+\ldots\ldots+m_n\vec{r}_n}{m1+m2+\ldots\ldots+m_n }; $$

$$\vec{r}_{cm}$$

निरंतर द्रव्यमान वितरण का केंद्र

$x_{c m}=\frac{\int x d m}{\int d m}, y_{c m}=\frac{\int y d m}{\int d m}, z_{c m}=\frac{\int z d m}{\int d m}$

$\int \mathrm{dm}=\mathrm{M}$ (शरीर का द्रव्यमान)

कुछ सामान्य प्रणालियों के द्रव्यमान का केंद्र

$\Rightarrow \quad$ दो बिंदु द्रव्यमानों की एक प्रणाली $m_{1} r_{1}=m_{2} r_{2}$

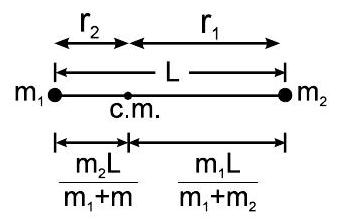
द्रव्यमान का केंद्र भारी द्रव्यमान के करीब स्थित होता है।

$\Rightarrow \quad$ आयताकार प्लेट (समरूपता द्वारा)

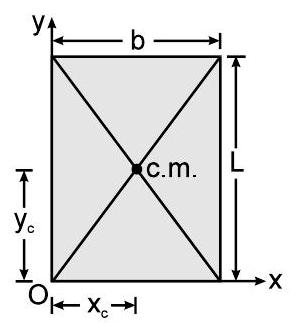
$ x_c=\frac{b}{2} \quad y_c=\frac{L}{2} $

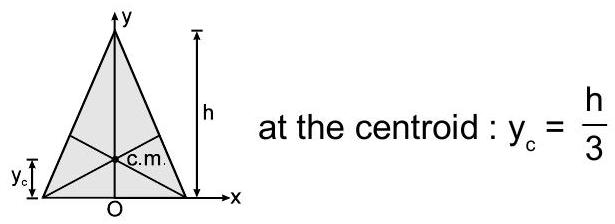
$\Rightarrow \quad$ एक त्रिकोणीय प्लेट (गुणात्मक तर्क से)

$\Rightarrow \quad$ एक अर्धवृत्ताकार वलय

$\Rightarrow \quad$ एक अर्धवृत्ताकार डिस्क

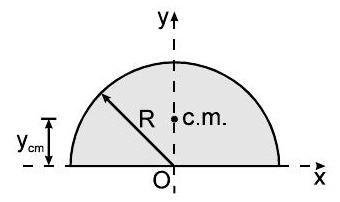
$$ y_{c}=\frac{4 R}{3 \pi} \quad x_{c}=0 $$

$\Rightarrow \quad$ एक अर्धगोलाकार खोल

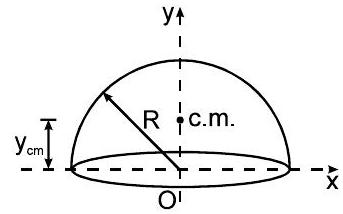
$$ y_{c}=\frac{R}{2} \quad x_{c}=0 $$

$\Rightarrow \quad$ एक ठोस गोलार्ध

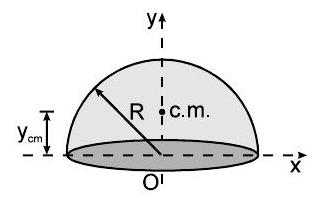
$$ y_c=\frac{3 R}{8} \quad x_c=O $$

$\Rightarrow \quad$ एक गोलाकार शंकु (ठोस)

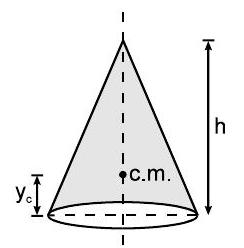
$$ \mathrm{y}_{\mathrm{c}}=\frac{\mathrm{h}}{4} $$

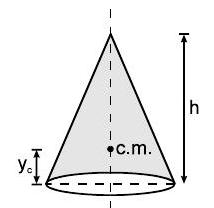
$$ \mathrm{y}_{\mathrm{c}}=\frac{\mathrm{h}}{3} $$

द्रव्यमान के केंद्र की गति और गति का संरक्षण:

सिस्टम के द्रव्यमान के केंद्र का वेग

$$ \vec{V}_{cm} = \frac{m_1\frac{\vec{dr}_1}{dt}+m2\frac{\vec{dr_2}}{dt}+m3\frac{\vec{dr_3 }}{dt}\ldots\ldots+m_n\vec{\frac{dr_n}{dt}}}{M} $$

$$ =\frac{m1\vec{V_1}+m2\vec{V_2}+m3\vec{V_3}+\ldots\ldots+m_n \vec{v}_n}{M} $$

$ \vec{P_{System}} = M \vec{V}_{cm} $

सिस्टम के द्रव्यमान के केंद्र का त्वरण

$ \vec{a}_{सेमी} = \frac{m_1\frac{\vec{dr}_1}{dt}+m2\frac{\vec{dr_2}}{dt}+m3\frac{\vec{dr_3}}{dt}\ldots\ldots +m_n\vec{\frac{dr_n}{dt}}}{M} $

$$ =\frac{m_1\vec{a_1}+m_2\vec{a_2}+m_3\vec{a_3}\ldots\ldots+m_n\vec{a_n}}{M} $$

$$ =\frac{\text { सिस्टम पर नेट बल }}{M} $$

$$ =\frac{\text { शुद्ध बाहरी बल }+ \text { शुद्ध आंतरिक बल }}{M} $$

$$ =\frac{\text { शुद्ध बाह्य बल }}{M} $$

$$ \vec{F_{ext}} = M\vec{a_{cm}} $$

आवेग

किसी बल का आवेग $F$ किसी पिंड पर कार्रवाई को इस प्रकार परिभाषित किया गया है:-

$$ \vec{J}=\int_{t_{i}}^{t_{f}} F dt \quad \vec{J}=\Delta \vec{P} $$

$$ \text { (आवेग - संवेग प्रमेय) } $$

महत्वपूर्ण बिंदु :

1. गुरुत्वाकर्षण बल और स्प्रिंग बल सदैव आवेगहीन होते हैं। 2. एक आवेगशील बल को केवल दूसरे आवेगशील बल द्वारा ही संतुलित किया जा सकता है।

पुनर्स्थापन गुणांक (ई)

$e=\frac{\text { Impulse of reformation }}{\text { Impulse of deformation }}=\frac{\int F_{r} d t}{\int F_{d} d t}$

$=s \frac{\text { Velocity of separation along line of impact }}{\text { Velocity of approach along line of impact }}$

परिवर्तनीय द्रव्यमान प्रणाली:

यदि किसी सिस्टम में दर से कोई द्रव्यमान जोड़ा या निकाला जाता है $\mu \mathrm{kg} / \mathrm{s}$ और सापेक्ष वेग $\vec{v_{rel}}$ (सिस्टम के बारे में), तो इस द्रव्यमान द्वारा सिस्टम पर लगाए गए बल का परिमाण होता है $\mu\left|\vec{v}_{\text {rel }}\right|$.

ज़ोर $\left(\vec{F}_{t}\right)$

$\vec{F_t}=\vec{v_{rel}}\left(\frac{dm}{dt}\right)$

रॉकेट प्रणोदन:

यदि गुरुत्वाकर्षण और रॉकेट के प्रारंभिक वेग को नजरअंदाज कर दिया जाए $u=0$;

$v=v_{r} \ln \left(\frac{m_{0}}{m}\right)$.