1. किसी बिंदु का वेक्टर प्रतिनिधित्व: बिंदु की स्थिति वेक्टर $P(x, y, z)$ है $x \hat{i}+y \hat{j}+z \hat{k}$.

2. दूरी सूत्र: $\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}+\left(z_{1}-z_{2}\right)^{2}}, \quad A B=|\overrightarrow{O B}-\overrightarrow{O A}|$

3. की दूरी $P$ निर्देशांक अक्षों से : $P A=\sqrt{y^{2}+z^{2}}, P B=\sqrt{z^{2}+x^{2}}, P C=\sqrt{x^{2}+y^{2}}$

4. अनुभाग सूत्र:

$x=\frac{m x_{2}+n x_{1}}{m+n} ,y=\frac{m y_{2}+n y_{1}}{m+n}, z=\frac{m z_{2}+n z_{1}}{m+n}$

मध्य बिंदु: $x=\frac{x_{1}+x_{2}}{2}, y=\frac{y_{1}+y_{2}}{2}, z=\frac{z_{1}+z_{2}}{2}$

5. दिशा कोसाइन और दिशा अनुपात

(i) दिशा कोसाइन: चलो $\alpha, \beta, \gamma$ वे कोण हों जो एक निर्देशित रेखा अक्षों की धनात्मक दिशाओं के साथ बनाती है $x, y$ और $z$ क्रमशः, फिर $\cos \alpha, \cos \beta, \cos \gamma$ रेखा की दिशा कोज्या कहलाती हैं। दिशा कोज्या आमतौर पर द्वारा निरूपित की जाती है $(\ell, \mathrm{m}, \mathrm{n})$. इस प्रकार $\ell=\cos \alpha, \mathrm{m}=$ $\cos \beta, \mathrm{n}=\cos \gamma$.

(ii) यदि $\ell, \mathrm{m}, \mathrm{n}$ तो, एक रेखा की दिक्-कोज्या हो $\ell^{2}+\mathrm{m}^{2}+\mathrm{n}^{2}=1$

(iii) दिशा अनुपात: चलो $\mathrm{a}, \mathrm{b}, \mathrm{c}$ दिशा कोज्या के समानुपाती हो $\ell, \mathrm{m}, \mathrm{n}$ तब $\mathrm{a}, \mathrm{b}, \mathrm{c}$ दिशा अनुपात कहलाते हैं

(iv) यदि $\ell, \mathrm{m}, \mathrm{n}$ दिशा कोज्या हो और $\mathrm{a}, \mathrm{b}, \mathrm{c}$ फिर, एक वेक्टर का दिशा अनुपात हो

$ \ell= \pm \frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, m= \pm \frac{b}{\sqrt{a^{ 2}+b^{2}+c^{2}}}, n= \pm \frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}} $

(vi) यदि निर्देशांक $P$ और $Q$ हैं $\left(x_{1}, y_{1}, z_{1}\right)$ और $\left(x_{2}, y_{2}, z_{2}\right)$ फिर रेखा का दिशा अनुपात $P Q$ क्षेत्र $=x_{2}-x_{1}, b=y_{2}-y_{1} \hspace{1mm}$ & $\hspace{1mm} c=z_{2}-z_{1}$ और रेखा की दिशा सहज्या $P Q$ हैं $\ell=\frac{x_{2}-x_{1}}{|P Q|}$, एम $=\frac{y_2 - y_1}{|PQ|} $ और $ n =\frac{z_2 - z_1} {|PQ|}$

6. दो रेखाखंडों के बीच का कोण:

$\cos \theta=\left|\frac{a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\right|$.

रेखा लंबवत होगी यदि $a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}=0$, समानांतर यदि $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

7. एक रेखा पर रेखाखंड का प्रक्षेपण

अगर $P (x_{1}, y_{1} , z_{1})$ और $Q\left(x_{2}, y_{2}, z_{2}\right)$ फिर का प्रक्षेपण $P Q$ दिशा-कोज्या वाली एक रेखा पर $\ell, m, n$ है

$|\ell ( x_2 - x_1 ) + m ( y_2 - y_1 ) + n ( z_2 - z_1 )|$

8. एक समतल का समीकरण : सामान्य रूप : $a x+b y+c z+d=0$, कहाँ $a, b, c$ सभी शून्य नहीं हैं, $a, b, c, d \in R$.

(i) सामान्य रूप : $\ell x+m y+n z=p$

(ii) बिंदु से होकर समतल $\left(x_{1}, y_{1}, z_{1}\right): a\left(x-x_{1}\right)+b\left(y-y_{1}\right)+c\left(z-z_{1}\right)=0$

(iii) अवरोधन प्रपत्र: $\frac{\mathrm{x}}{\mathrm{a}}+\frac{\mathrm{y}}{\mathrm{b}}+\frac{\mathrm{z}}{\mathrm{c}}=1$

(iv) वेक्टर रूप: $(\vec{r}-\vec{a}) \cdot \vec{n}=0$ या $\vec{r} \cdot \vec{n}=\vec{a} \cdot \vec{n}$

(v) दिए गए तल के समानांतर कोई भी तल $\mathrm{ax}+\mathrm{by}+\mathrm{cz}+\mathrm{d}=0$ है $\mathrm{ax}+\mathrm{by}+\mathrm{cz}+\lambda=0$

बीच की दूरी $a x+b y+c z+d_{1}=0$ और $a x+b y+c z+d_{2}=0$ है $=\frac{\left|d_{1}-d_{2}\right|}{\sqrt{a^{2}+b^{2}+c^{2}}}$

(vi) दिए गए सदिशों के समानांतर किसी दिए गए बिंदु से गुजरने वाले समतल का समीकरण:

$\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{a}}+\lambda \overrightarrow{\mathrm{b}}+\mu \overrightarrow{\mathrm{c}}$ (पैरामीट्रिक फॉर्म) कहां $\lambda \hspace{1mm} $& $ \hspace{1mm} \mu$ अदिश हैं

या $\quad \overrightarrow{\mathrm{r}} \cdot(\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}})=\overrightarrow{\mathrm{a}} \cdot(\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}}) \quad$ (गैर पैरामीट्रिक फॉर्म)

9. एक समतल & एक बिंदु

(i) बिंदु की दूरी $\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$ विमान से $a x+b y+c z+d=0$ द्वारा दिया गया है $\frac{a x^{\prime}+b y^{\prime}+c z^{\prime}+d}{\sqrt{a^{2}+b^{2}+c^{2}}}$.

(ii) एक बिंदु से लम्ब की लंबाई ( $\vec{a}$ ) शीर्ष लेन $\vec{r} \cdot \vec{n}=d$ द्वारा दिया गया है $p=\frac{|\vec{a} \cdot \vec{n}-d|}{|\vec{n}|}$.

(iii) पैर $\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$ बिंदु से खींचे गये लम्ब का $\left(x_{1}, y_{1}, z_{1}\right)$ विमान के लिए $a x+b y+c z+d=0$ द्वारा दिया गया है

$\frac{x^{\prime}-x_{1}}{a}=\frac{y^{\prime}-y_{1}}{b}=\frac{z^{\prime}-z_{1}}{c}=-\frac{\left(a x_{1}+b y_{1}+c z_{1}+d\right)}{a^{2}+b^{2}+c^{2}}$

(iv) समतल पर किसी बिंदु का प्रतिबिम्ब ढूँढने के लिए:

होने देना $P\left(x_{1}, y_{1}, z_{1}\right)$ एक दिया गया बिंदु है और $a x+b y+c z+d=0$ दिया गया है समतल चलो $\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$ छवि बिंदु है. तब

$\frac{x^{\prime}-x_{1}}{a}=\frac{y^{\prime}-y_{1}}{b}=\frac{z^{\prime}-z_{1}}{c}=-2 \frac{\left(a x_{1}+b y_{1}+c z_{1}+d\right)}{a^{2}+b^{2}+c^{2}}$

10. दो तलों के बीच का कोण:

$\cos \theta=\left|\frac{a a^{\prime}+b b^{\prime}+c c^{\prime}}{\sqrt{a^{2}+b^{2}+c^{2}} \sqrt{a^{\prime 2}+b^{\prime 2}+c^{\prime 2}}}\right|$

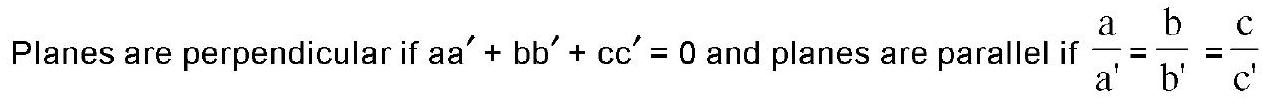
कोना $\theta$ विमानों के बीच $\vec{r} \cdot \vec{n}_1 = d_1 $ और $\vec{r} \cdot \vec{n}_2 = d_2 $ द्वारा दिया गया है, $\cos \theta=\frac{\vec{n}_1 \cdot \vec{n}_2}{|\vec{n}_1 | \cdot|\vec{n}_2|}$

विमान लंबवत हैं यदि $\vec{n}_{1} \cdot \vec{n}_2 = 0 $ & विमान समानांतर हैं यदि $\vec{n}_1 = \lambda \hspace{1mm} \vec{n}_2, \lambda $ एक अदिश राशि है

11. कोण समद्विभाजक

(i) दो दिए गए समतलों के बीच के कोण को समद्विभाजित करने वाले समतलों के समीकरण

$a_{1} x+b_{1} y+c_{1} z+d_{1}=0$ और $a_{2} x+b_{2} y+c_{2} z+d_{2}=0$ हैं

$\frac{a_{1} x+b_{1} y+c_{1} z+d_{1}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}}= \pm \frac{a_{2} x+b_{2} y+c_{2} z+d_{2}}{\sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}$

(ii) न्यून/अधिक कोण का समद्विभाजक: सबसे पहले दोनों अचर पदों को धनात्मक बनाएं। तब

$a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}>0 \Rightarrow$ मूल अधिक कोण पर स्थित है

$a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} < 0 \Rightarrow$ मूल न्यूनकोण में है

12. विमानों का परिवार

(i) के चौराहे से होकर गुजरने वाला कोई भी विमान $a_{1} x + b_{1} y+c_{1} z + d_{1}= 0 \hspace{1mm}$ &amp; $ \hspace{1mm} a_{2} x+b_{2} y+c_{2} z+d_{2}=0$ है $a_{1} x+b_{1} y+c_{1} z+d_{1}+\lambda\left(a_{2} x+b_{2} y+c_{2} z+d_{2}\right)=0$

(ii) समतलों के प्रतिच्छेदन से गुजरने वाले समतल का समीकरण $\vec{r} . \vec{n}_1 = d_1 \hspace{1mm} $ &amp; $\hspace{1mm}\vec{r} . \vec{n}_2 = d_2 $ है $\vec{r} \cdot (n_1 + \lambda \vec{n}_2) = d_1 + \lambda d_2 $ कहाँ $\lambda $ मनमाना अदिश राशि है

13. त्रिभुज का क्षेत्रफल : दो सदिश से $\tiny{\overrightarrow{A B}}$ और $\tiny{\overrightarrow{A C}}$. फिर क्षेत्रफल दिया गया है $\tiny{\frac{1}{2}|\overrightarrow{A B} \times \overrightarrow{A C}|}$

14.