1. साइन नियम: $\quad \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$.

2. कोज्या सूत्र:

(मैं) $\cos A=\frac{b^{2}+c^{2}-a^{2}}{2 b c}$

(ii) $\cos B=\frac{c^{2}+a^{2}-b^{2}}{2 c a} $

(iii) $\cos C=\frac{a^{2}+b^{2}-c^{2}}{2 a b}$

3. प्रक्षेपण सूत्र:

(मैं) $a=b \cos C+c \cos B$

(ii) $b=c \cos A+a \cos C$

(iii) $c=a \cos B+b \cos A$

4. नेपियर की सादृश्यता - स्पर्शरेखा नियम:

(मैं) $\tan \frac{\mathrm{B}-\mathrm{C}}{2}=\frac{\mathrm{b}-\mathrm{c}}{\mathrm{b}+\mathrm{c}} \cot \frac{\mathrm{A}}{2}$

(ii) $\tan \frac{C-A}{2}=\frac{c-a}{c+a} \cot \frac{B}{2}$

(iii) $\tan \frac{A-B}{2}=\frac{a-b}{a+b} \cot \frac{C}{2}$

5. आधे कोणों के त्रिकोणमितीय फलन:

(मैं) $\quad \sin \frac{\Lambda}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}{\mathrm{bc}}} ; \sin \frac{\mathrm{B}}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{c})(\mathrm{s}-\mathrm{a})}{\mathrm{ca}}} ; \sin \frac{\mathrm{C}}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{a})(\mathrm{s}-\mathrm{b})}{\mathrm{ab}}}$

(ii) $\quad \cos \frac{\mathrm{A}}{2}=\sqrt{\frac{\mathrm{s}(\mathrm{s}-\mathrm{a})}{\mathrm{bc}}} ; \cos \frac{\mathrm{B}}{2}=\sqrt{\frac{\mathrm{s}(\mathrm{s}-\mathrm{b})}{\mathrm{ca}}} ; \cos \frac{\mathrm{C}}{2}=\sqrt{\frac{\mathrm{s}(\mathrm{s}-\mathrm{c})}{\mathrm{ab}}}$

(iii) $\tan \frac{\Lambda}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}{\mathrm{s}(\mathrm{s}-\mathrm{a})}}=\frac{\Delta}{\mathrm{s}(\mathrm{s}-\mathrm{a})}$

कहाँ $\mathrm{s}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}\hspace{1mm} \text{ is semi perimetre of triangle.}$

(iv) $ \sin A=\frac{2}{bc} \sqrt{s(sa)(sb)(sc)}=\frac{2 \Delta}{bc} $

6. त्रिभुज का क्षेत्रफल $(\Delta): \hspace{1mm} \Delta=\frac{1}{2} a b \sin C=\frac{1}{2} b c \sin A=\frac{1}{2} c a \sin B=\sqrt{s(s-a)(s-b)(s-c)}$

7. $\mathbf{m}$-एन नियम:

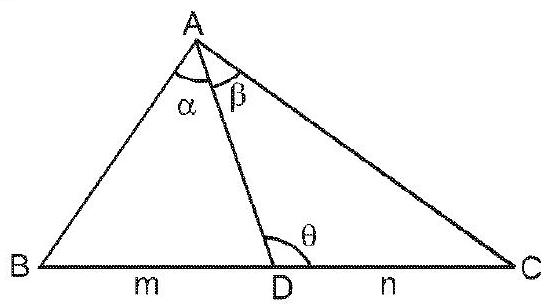
$If B D: D C=m: n, then$

$If B D: D C=m: n, then$

$ \शुरू{संरेखित} (m+n) \cot \थीटा और =m \cot \alpha-n \cot \beta \ & =n \cot Bm \cot C \अंत{संरेखित} $

8. परिधि की त्रिज्या :

$$ R=\frac{a}{2 \sin A}=\frac{b}{2 \sin B}=\frac{c}{2 \sin C}=\frac{abc}{4 \Delta} $$

9. अंतःवृत्त की त्रिज्या :

(मैं) $r=\frac{\Delta}{s}$

(ii) $r=(s-a) \tan \frac{A}{2}=(s-b) \tan \frac{B}{2}=(s-c) \tan \frac{C}{2}$

(iii) $r=\frac{a \sin \frac{B}{2} \sin \frac{C}{2}}{\cos \frac{A}{2}}\hspace{1mm} $ & जल्द ही

(iv) $r=4 R \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}$

10. पूर्व वृत्तों की त्रिज्या :

(मैं) $r_{1}=\frac{\Delta}{s-a} ; r_{2}=\frac{\Delta}{s-b} ; r_{3}=\frac{\Delta}{s-c}$

(ii) $r_{1}=s \tan \frac{A}{2} ; r_{2}=s \tan \frac{B}{2} ; r_{3}=s \tan \frac{\mathrm{C}}{2}$

(iii) $r_{1}=\frac{a \cos \frac{B}{2} \cos \frac{C}{2}}{\cos \frac{A}{2}}\hspace{1mm}$ & जल्द ही

(iv) $r_{1}=4 R \sin \frac{A}{2} \cdot \cos \frac{B}{2} \cdot \cos \frac{C}{2}$

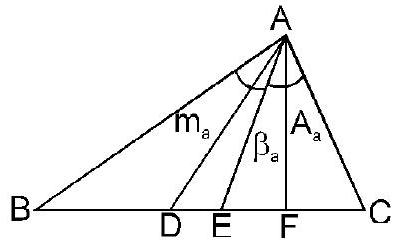
11. कोण के समद्विभाजक, माध्यिका और ऊंचाई की लंबाई:

(i) कोण से कोण के समद्विभाजक की लंबाई $A=\beta_{a}=\frac{2 b c \cos \frac{A}{2}}{b+c}$;

(ii) कोण से माध्यिका की लंबाई $A=m_{a}=\frac{1}{2} \sqrt{2 b^{2}+2 c^{2}-a^{2}}$

$ \text { (iii) कोण से ऊंचाई की लंबाई } A=A_{a}=\frac{2 \Delta}{a} $

12. त्रिभुज के शीर्षों और भुजाओं से विशेष बिंदुओं की दूरियाँ:

(i)परिकेंद्र (O) : $O A=R \hspace{1mm}$&$\hspace{1mm} O_{a}=R \cos A$

(ii) अंतःकेंद्र (I): $I A=r \operatorname{cosec} \frac{A}{2} \hspace{1mm} $ & $\hspace{1mm} I_{a}=r$

(iii) एक्सेंटर $\left(I_{1}\right): I_{1} A=r_{1} \operatorname{cosec} \frac{A}{2}$

(iv) ऑर्थोसेंटर: $H A=2 R \cos A \hspace{1mm} $& $\hspace{1mm} H_{a}=2 R \cos B \cos C$

(v) सेंट्रोइड (जी): जीए $=\frac{1}{3} \sqrt{2 b^{2}+2 c^{2}-a^{2}} \quad$ & $\quad G_{a}=\frac{2 \Delta}{3 a}$

13. ऑर्थोसेंटर और पेडल त्रिकोण:

ऊँचाईयों के पादों को मिलाने से जो त्रिभुज KLM बनता है उसे पैडल त्रिभुज कहते हैं।

(i) इसके कोण हैं $\pi-2 A, \pi-2 B$ और $\pi-2 C$.

(ii) इसकी भुजाएँ हैं a $\cos A=R \sin 2 A$,

$ b \cos B=R \sin 2 B \hspace{1mm} \text { और } \hspace{1mm} c \cos C=R \sin 2 C $

(iii) त्रिभुजों की परिधि $\mathrm{PBC}, \mathrm{PCA}, \mathrm{PAB}$ और $\mathrm{ABC}$ बराबर हैं।

14. बाह्यत्रिकोण:

तीनों बाह्यकेंद्रों को मिलाने से जो त्रिभुज बनता है $I_{1}, I_{2}$ और $I_{3}$ का $\triangle A B C$ बाह्यकेन्द्रीय या बाह्यकेन्द्रीय त्रिभुज कहलाता है।

(मैं) $\triangle ABC$ का पैडल त्रिकोण है $\Delta I_1 I_2 I_3$.

(ii) इसके कोण हैं $\frac{\pi}{2}-\frac{A}{2}, \frac{\pi}{2}-\frac{B}{2} \hspace{1mm}$ & $\hspace{1mm}\frac{\pi}{2}-\frac{C}{2}$.

(iii) इसकी भुजाएँ हैं $4 R \cos \frac{A}{2}, 4 R \cos \frac{B}{2}\hspace{1mm}$ & $\hspace{1mm} 4 R \cos \frac{C}{2}$.

(iv) $ I_{1}=4 R \sin \frac{A}{2} ; I I_{2}=4 R \sin \frac{B}{2} ; I I_{3}=4 R \sin \frac{C}{2}$.

(v) अंतःकेंद्र I $\triangle A B C$ एक्सेंट्रल का ऑर्थोसेंटर है $\Delta I_1 I_2 I_3$.

15. विशेष बिंदुओं के बीच की दूरी :

(i) परिकेंद्र और लंबकेंद्र के बीच की दूरी

$\mathrm{OH}^{2}=\mathrm{R}^{2}(1-8 \cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C})$

(ii) परिकेन्द्र और अंतःकेन्द्र के बीच की दूरी

$\mathrm{OI}^{2}=\mathrm{R}^{2}\left(1-8 \sin \frac{\mathrm{A}}{2} \sin \frac{\mathrm{B}}{2} \sin \frac{\mathrm{C}}{2}\right)=\mathrm{R}^{2}-2 \mathrm{Rr}$

(iii) परिकेंद्र और केन्द्रक के बीच की दूरी

$O G^{2}=R^{2}-\frac{1}{9}\left(a^{2}+b^{2}+c^{2}\right)$