1. स्पर्शरेखा और सामान्य का समीकरण

पर स्पर्शरेखा $\left(x_{1}, y_{1}\right)$ द्वारा दिया गया है $\left(y-y_{1}\right)=f^{\prime}\left(x_{1}\right)\left(x-x_{1}\right)$; कब, $f^{\prime}\left(x_{1}\right)$ यह सचमुच का है।

और सामान्य पर $\left(x_{1}, y_{1}\right)$ है $\left(y-y_{1}\right)=-\frac{1}{f^{\prime}\left(x_{1}\right)}\left(x-x_{1}\right)$, कब $f^{\prime}\left(x_{1}\right)$ शून्येतर वास्तविक है.

2. किसी बाहरी बिंदु से स्पर्शरेखा

एक बिंदु दिया गया $P(a, b)$ जो वक्र पर स्थित नहीं है $y=f(x)$, फिर वक्र की संभावित स्पर्श रेखाओं का समीकरण $y=f(x)$, के माध्यम से गुजरते हुए $(a, b)$ संपर्क बिंदु को हल करके पाया जा सकता है $Q$.

$f^{\prime}(h)=\frac{f(h)-b}{h-a}$

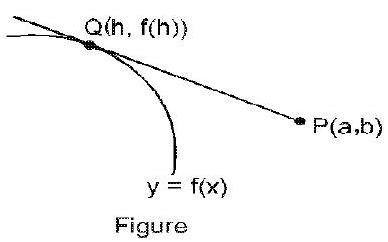
और स्पर्शरेखा का समीकरण है $y-b=\frac{f(h)-b}{h-a}(x-a)$

3. स्पर्शरेखा की लंबाई, सामान्य, उपस्पर्शरेखा, उपसामान्य

(मैं) $\mathrm{PT}=|\mathrm{k}| \sqrt{1+\frac{1}{\mathrm{~m}^{2}}}=$ स्पर्शरेखा की लंबाई

(ii) $\mathrm{PN}=|\mathrm{k}| \sqrt{1+\mathrm{m}^{2}}=\text { Length of Normal }$

(iii) $T M=\left|\frac{k}{m}\right|=$ उपस्पर्शरेखा की लंबाई

(iv) $\mathrm{MN}=|\mathrm{km}|=$ असामान्य की लंबाई.

4.$\hspace{1mm} $ वक्रों के बीच का कोण

दो प्रतिच्छेदी वक्रों के बीच के कोण को दो वक्रों के प्रतिच्छेदन बिंदु पर उनकी स्पर्शरेखाओं (या अभिलंबों) के बीच तीव्र कोण के रूप में परिभाषित किया गया है (जैसा कि चित्र में दिखाया गया है)।

$$ \tan \theta=\left|\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}\right| $$

5. दो वक्रों के बीच की न्यूनतम दूरी

दो अप्रतिच्छेदी अवकलनीय वक्रों के बीच की न्यूनतम दूरी सदैव उनके उभयनिष्ठ अभिलंब के अनुदिश होती है। (जहां भी परिभाषित हो)

6. रोले का प्रमेय :

यदि कोई फ़ंक्शन $f$ पर परिभाषित $[a, b]$ है:

(i) निरंतर चालू $[a, b]$

(ii) पर व्युत्पन्न $(a, b)$ और

(iii) $f(a)=f(b)$,

तब कम से कम एक वास्तविक संख्या मौजूद होती है $c$ बीच में $a$ और $b(a<c<b)$ ऐसा है कि $f^{\prime}(c)=0$

7. लैग्रेंज का माध्य मान प्रमेय (एलएमवीटी) :

यदि कोई फ़ंक्शन $f$ पर परिभाषित $[a, b]$ है

(i) निरंतर चालू $[a, b]$ और

(ii) पर व्युत्पन्न $(a, b)$

तो a और के बीच कम से कम एक वास्तविक संख्या मौजूद होती है $b(a<c<b)$ ऐसा है कि $\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)$

8. याद रखने योग्य क्षेत्रमिति के उपयोगी सूत्र :

(1) घनाभ का आयतन $=\ell \mathrm{bh}$.

(2) घनाभ का पृष्ठीय क्षेत्रफल $=2(\ell b+b h+h \ell)$.

(3) घन का आयतन $=\mathbf{a}^{3}$

(4) घन का पृष्ठीय क्षेत्रफल $=6 a^{2}$

(5) शंकु का आयतन $=\frac{1}{3} \pi r^{2} h$.

(6) शंकु का वक्र पृष्ठीय क्षेत्रफल $=\pi \mathrm{r} \ell(\ell=$ तिरछी ऊंचाई $)$

(7) बेलन का वक्र पृष्ठीय क्षेत्रफल $=2 \pi \mathrm{rh}$.

(8) सिलेंडर का कुल सतह क्षेत्र $=2 \pi r h+2 \pi r^{2}$.

(9) गोले का आयतन $=\frac{4}{3} \pi r^{3}$.

(10) गोले का पृष्ठीय क्षेत्रफल $=4 \pi r^{2}$.

(11) वृत्ताकार त्रिज्यखंड का क्षेत्रफल $=\frac{1}{2} r^{2} \theta$, कब $\theta$ रेडियन में है.

(12) प्रिज्म का आयतन $=$ (आधार का क्षेत्रफल) $\times$ (ऊंचाई)।

(13) प्रिज्म का पार्श्व सतह क्षेत्र $=$ (आधार की परिधि) $\times$ (ऊंचाई)।

(14) प्रिज्म का कुल पृष्ठीय क्षेत्रफल $=$ (पार्श्व सतह क्षेत्र $)+2$ (आधार का क्षेत्रफल) (ध्यान दें कि प्रिज्म की सभी पार्श्व सतहें आयताकार होती हैं)।

(15)पिरामिड का आयतन $=\frac{1}{3}$ (आधार का क्षेत्रफल) $\times($ ऊंचाई ।

(16) पिरामिड का घुमावदार सतह क्षेत्र $=\frac{1}{2}$ (आधार की परिधि $) \times($ तिरछी ऊंचाई)। (ध्यान दें कि पिरामिड की तिरछी सतहें त्रिभुज होती हैं)।