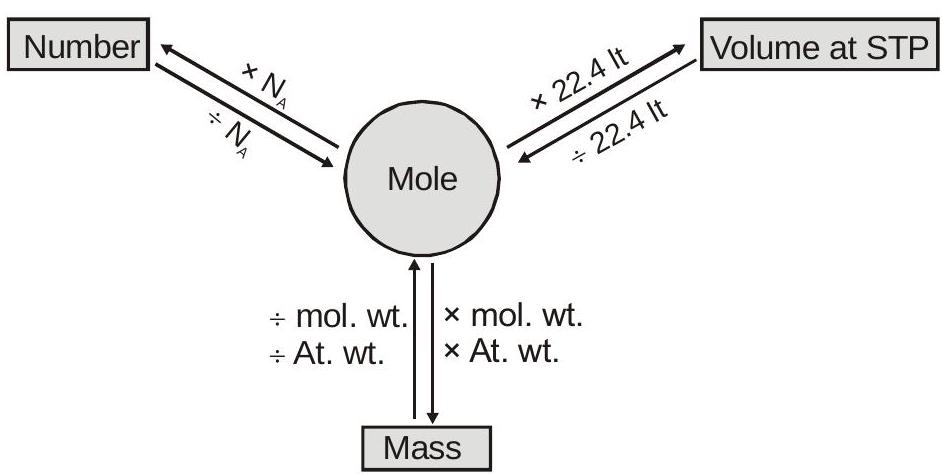
सापेक्ष परमाणु द्रव्यमान (RAM)

$$=\frac{\text { Mass of one atom of an element }}{\frac{1}{12} \times \text { mass of one carbonatom }}$$

$=$ न्यूक्लियॉन की कुल संख्या

वाई-मैप

घनत्व:

$$ \text { विशिष्ट गुरुत्व }=\frac{\text { पदार्थ का घनत्व }}{\text { पानी का घनत्व } 4^{\circ} \mathrm{C}} $$

गैसों के लिए:

पूर्ण घनत्व (द्रव्यमान/आयतन)

$=\frac{\text { Molar mass of the gas }}{\text { Molar volume of the gas }}$

$\Rightarrow \rho=\frac{\mathrm{PM}}{\mathrm{RT}}$

वाष्प घनत्व वी.डी $=\frac{d_{\text {gas }}}{d_{H_{2}}}=\frac{P M_{\text {gas } / R T}}{P_{H_{2} / R T}}=\frac{M_{\text {gas }}}{M_{H_{2}}}=\frac{M_{\text {gas }}}{2}$ $M_{\text {gas }}=2$ वीडी

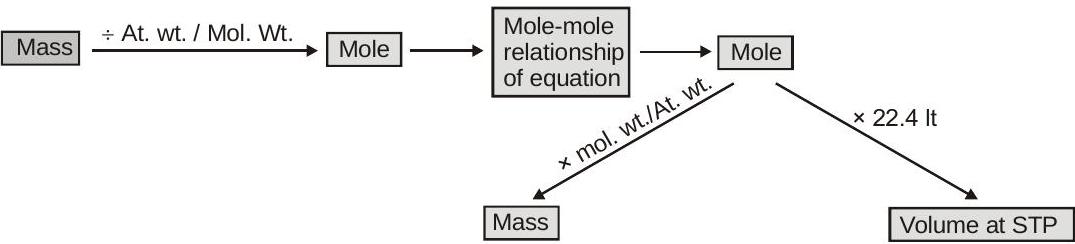
तिल-तिल विश्लेषण:

एकाग्रता शर्तें:

मोलैरिटी (एम):

$$ \इसलिए \quad \text { मोलरिटी }(\mathrm{M})=\frac{\mathrm{W} \times 1000}{(\text { mol. wt of solute }) \times \mathrm{V}_{ \पाठ {आईएनएमएल }}} $$

मोलैलिटी (एम):

$$ मोललता =\frac{\text{विलेय के मोलों की संख्या} }{\text{ग्राम में विलायक का द्रव्यमान}}\गुना 1000 $$

$$ = \frac{1000 \times W_1}{M_1 \times w_2} $$

मोल - अंश $(x)$ :

$\therefore \quad$ विलयन का मोल अंश $\left(\mathrm{x}_{1}\right)=\frac{\mathrm{n}}{\mathrm{n}+\mathrm{N}}$

$\therefore \quad$ विलायक का मोल अंश $\left(\mathrm{x}_{2}\right)=\frac{\mathrm{N}}{\mathrm{n}+\mathrm{N}}$

$\quad \quad x_{1}+x_{2}=1$

% गणना :

$\quad \quad$ (मैं) $\ \%\mathrm{w} / \mathrm{w}=\frac{\text { mass of solute in } \mathrm{gm}}{\text { mass of solution in } \mathrm{gm}} \times 100$

$\quad \quad$ (ii) $\ \%\mathrm{w} / \mathrm{v}=\frac{\text { mass of solute in } \mathrm{gm}}{\text { Volume of solution in } \mathrm{ml}} \times 100$

$\quad \quad$ (iii) $\ \%\mathrm{v} / \mathrm{v}=\frac{\text { Volume of solute in } \mathrm{ml}}{\text { Volume of solution }} \times 100$

निम्नलिखित रूपांतरण प्राप्त करें:

(1) विलेय का मोल अंश विलयन की मोलरता में $M=\frac{x_{2} \rho \times 1000}{x_{1} M_{1}+M_{2} x_{2}}$

(2) मोलरिटी को मोल अंश में $ x_2 = \frac{MM_1 \times 1000}{\rho \times 1000 - MM_2} $

(3) मोल अंश मोललिटी में $m=\frac{x_{2} \times 1000}{x_{1} M_{1}}$

(4) मोललता मोल अंश में $ x_2 = \frac{mM_1}{1000 + mM_1} $

(5) मोललता से मोलरता $M=\frac{m \rho \times 1000}{1000+\mathrm{mM}_{2}}$

(6) मोलरता में मोलरता $\mathrm{m}=\frac{\mathrm{M} \times 1000}{1000 \rho-\mathrm{MM}_{2}}$

$M_{1}$ और $M_{2}$ विलायक और विलेय के दाढ़ द्रव्यमान हैं। $\rho$ समाधान का घनत्व है $(\mathrm{gm} / \mathrm{mL})$

$M=$ मोलरिटी (मोल/लीटर), $m=$ मोलैलिटी (मोल $/ \mathrm{kg}$ ), $x_{1}=$ विलायक का मोल अंश, $x_{2}=$ विलेय का मोल अंश

औसत/माध्य परमाणु द्रव्यमान:

$$ A_{x}=\frac{a_{1} x_{1}+a_{2} x_{2}+\ldots। .+a_{n} x_{n}{100} $$

माध्य दाढ़ द्रव्यमान या आणविक द्रव्यमान

$$ एम_{\पाठ {औसत. }}=\frac{n_{1} M_{1}+n_{2} M_{2}+\ldots . . n_{n} M_{n}}{n_{1}+n_{2}+\ldots n_{n}} \quad \text { या }$$

$$\क्वाड एम_{\पाठ {औसत। ! $$

व्यक्तिगत ऑक्सीकरण संख्या की गणना:

सूत्र: ऑक्सीकरण संख्या $=$ संयोजकता कोश में इलेक्ट्रॉनों की संख्या - बंधन के बाद बचे इलेक्ट्रॉनों की संख्या

समतुल्य भार/द्रव्यमान की अवधारणा:

तत्वों के लिए, समतुल्य भार (ई)= $ \frac{\text { Atomic weight }}{\text { Valency }- \text { factor }}$

अम्ल/क्षार के लिए, $ \quad \mathrm{E}=\frac{\mathrm{M}}{\text { Basicity / Acidity }}$

कहाँ $\mathrm{M}=$ दाढ़ जन

ओए/आरए के लिए, $ \quad E=\frac{M}{\text { no. of moles of } \mathrm{e}^{-} \text {gained /lost }}$

समतुल्य वजन (ई) =$\frac{\text { Atomic or moleculear weight }}{v . f .}$

(vf $=$ संयोजकता कारक)

समकक्षों की संख्या की अवधारणा

विलेय के समकक्षों की संख्या $=\frac{W t}{E q \cdot \text { wt. }}=\frac{W}{E}=\frac{W}{M / n}$

विलेय के समकक्षों की संख्या $=$ विलेय के मोलों की संख्या $\times$ वी.एफ

सामान्यता (एन):

साधारण अवस्था $(N)=\frac{\text { Number of equivalents of solute }}{\text { Volume of solution (in litres) }}$

साधारण अवस्था $=$ मोलरिटी $\times$ वी.एफ

वैलेंस फैक्टर की गणना:

$\mathrm{n}$-अम्ल का कारक $=$ क्षारकता $=$ नहीं। का $\mathrm{H}^{+}$अम्ल के प्रति अणु में आयन सुसज्जित होते हैं।

$\mathrm{n}$-आधार का कारक $=$ अम्लता $=$ नहीं। का $\mathrm{OH}^{-}$आयन प्रति अणु आधार द्वारा सुसज्जित है।

समतुल्यता बिंदु पर

$ \quad N_1 \ V_1 = N_2 \ V_2 $

$\quad n_{1} M_{1} V_{1}=n_{2} M_{2} V_{2}$

की मात्रा शक्ति $ H_2 O_2 $ :

$20V H_2 O_2 $ मतलब इस नमूने का एक लीटर $H_2 O_2 $ विघटित होने पर 20 लीटर प्राप्त होता है। का $O_2$ एसटीपी पर गैस

की सामान्यता $ H_2 O_2 (N)= \frac{\text{Volume,strength of }H_2 O_2}{5.6}$

की मोलरता $ H_2 O_2 (M)= \frac{\text{Volume strength of }H_2 O_2}{11.2}$

कठोरता का माप:

पीपीएम में कठोरता $=\frac{\text { mass of } \mathrm{CaCO}_{3}}{\text { Total mass of water }} \times 10^{6}$

ब्लीचिंग पाउडर के नमूने से उपलब्ध क्लोरीन की गणना:

% का $Cl_2$ = $\frac{3.55 \times x \times V(mL)}{W(g)} $ कहाँ $\mathrm{x}=$ हाइपो समाधान की मात्रा

और $v=m L$. अनुमापन में प्रयुक्त हाइपो घोल का।