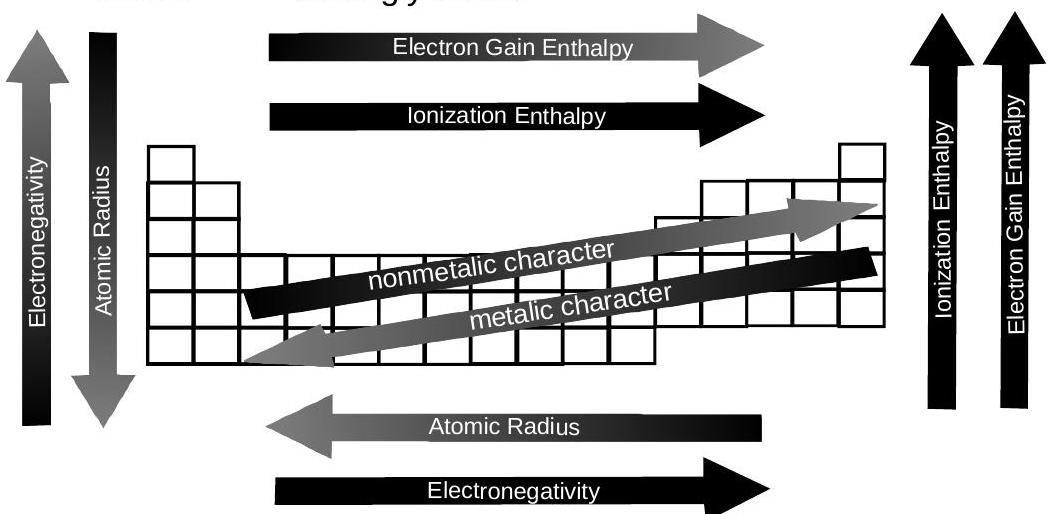
आवर्त सारणी और आवर्तता
आधुनिक आवर्त सारणी का विकास
(ए) डोबेराइनर के ट्रायड्स: उन्होंने समान तत्वों को तीन तत्वों के समूहों में व्यवस्थित किया जिन्हें ट्रायड्स कहा जाता है
(बी) न्यूलैंड का ऑक्टेव का नियम: वह तत्वों के रासायनिक गुणों को उनके परमाणु द्रव्यमान के साथ सहसंबंधित करने वाले पहले व्यक्ति थे।
(सी) लोथर मेयर का वर्गीकरण: उन्होंने कई तत्वों के लिए उनके संबंधित परमाणु आयतन के विरुद्ध परमाणु द्रव्यमान के बीच एक ग्राफ बनाया। उन्होंने अवलोकन पाया;
(i) समान गुणों वाले तत्व वक्र पर समान स्थिति रखते हैं,
(ii) बड़े परमाणु आयतन वाली क्षार धातुओं ने शिखरों पर कब्जा कर लिया,
(iii) संक्रमण तत्वों ने गर्तों पर कब्जा कर लिया,
(iv) अक्रिय गैसों से पहले हैलोजन ने वक्र के आरोही भागों पर कब्जा कर लिया
(v) क्षारीय पृथ्वी धातुओं ने वक्र के अवरोही भागों के मध्य बिंदुओं पर अपना स्थान बना लिया। इन अवलोकनों के आधार पर उन्होंने निष्कर्ष निकाला कि तत्वों के परमाणु आयतन (एक भौतिक गुण) उनके परमाणु द्रव्यमान के आवधिक कार्य हैं।
(डी) मेंडेलीव की आवर्त सारणी:
मेंडेलीव का आवर्त नियम
तत्वों के भौतिक और रासायनिक गुण उनके परमाणु द्रव्यमान के आवर्ती कार्य हैं।
मेंडलीफ की आवर्त सारणी के गुण:
- इसने तत्वों और उनके यौगिकों के अध्ययन को सरल और व्यवस्थित किया है।
- इसकी आवर्त सारणी में दिए गए रिक्त स्थानों के आधार पर नए तत्वों की खोज की भविष्यवाणी करने में मदद मिली है।
मेन्डेलीफ की आवर्त सारणी में दोष:
-
हाइड्रोजन की स्थिति अनिश्चित है। इसे IA और VIIA समूहों में रखा गया है
-
आइसोटोप को कोई अलग स्थान नहीं दिया गया।
-
आवर्त सारणी में लैंथेनाइड्स और एक्टिनाइड्स की असामान्य स्थिति।
-
आवर्त सारणी में तत्वों की व्यवस्था में परमाणु भार बढ़ाने के क्रम का कड़ाई से पालन नहीं किया जाता है।
-
समान तत्वों को अलग-अलग समूहों में रखा गया।
-
इसमें आवधिकता का कारण नहीं बताया गया।
(ई) आवर्त सारणी या मोसले की आवर्त सारणी का दीर्घ रूप :
आधुनिक आवर्त नियम (मोसले का आवर्त नियम):
आधुनिक आवर्त नियम (मोसले का आवर्त नियम)
यदि तत्वों को उनके बढ़ते परमाणु क्रमांक के क्रम में व्यवस्थित किया जाए, तो एक नियमित अंतराल के बाद समान गुणों वाले तत्वों की पुनरावृत्ति होती है।
आवधिकता:
जब तत्वों को बढ़ते हुए परमाणु क्रमांक के क्रम में व्यवस्थित किया जाता है तो नियमित अंतराल के बाद तत्वों के गुणों की पुनरावृत्ति को आवर्तता कहा जाता है।
आवधिकता का कारण:
तत्वों के गुणों की आवधिक पुनरावृत्ति निश्चित नियमित अंतराल के बाद समान संयोजकता कोश इलेक्ट्रॉनिक विन्यास की पुनरावृत्ति के कारण होती है।
आधुनिक आवर्त सारणी में क्षैतिज पंक्तियाँ (आवर्त) और ऊर्ध्वाधर स्तंभ (समूह) होते हैं।
अवधि:
सात अवधियों को 1, 2, 3, 4, 5, 6 और 7 के रूप में क्रमांकित किया गया है।
-
प्रत्येक आवर्त में समान संयोजकता कोश वाले तत्वों की एक श्रृंखला होती है।
-
प्रत्येक अवधि इसमें मौजूद वैलेंस शेल की एक विशेष प्रमुख क्वांटम संख्या से मेल खाती है।
-
प्रत्येक आवर्त एक क्षार धातु से शुरू होता है जिसका सबसे बाहरी इलेक्ट्रॉनिक विन्यास होता है।
-
प्रत्येक अवधि बाहरीतम इलेक्ट्रॉनिक विन्यास वाली एक उत्कृष्ट गैस के साथ समाप्त होती है $n s^{2} n p^{6}$ बाह्यतम इलेक्ट्रॉनिक विन्यास वाले हीलियम को छोड़कर $1 s^{2}$.
-
प्रत्येक काल की शुरुआत नई ऊर्जा स्तर भरने से होती है।
-
प्रत्येक आवर्त में तत्वों की संख्या भरे जाने वाले ऊर्जा स्तर में उपलब्ध परमाणु कक्षाओं की संख्या से दोगुनी है।
समूह:
अठारह समूह हैं जिनकी संख्या 1,2,3,4,5,…………13,14,15 है।$, $16,17,18.
समूह में समान संयोजकता कोश इलेक्ट्रॉनिक विन्यास वाले तत्वों की एक श्रृंखला होती है।
तत्वों का वर्गीकरण:
(ए) एस-ब्लॉक तत्व
समूह 1&2 तत्व एस-ब्लॉक का निर्माण करते हैं। सामान्य इलेक्ट्रॉनिक विन्यास [अक्रिय गैस] है $ns^{1-2}$.
एस-ब्लॉक तत्व आवर्त सारणी के सबसे बाईं ओर स्थित हैं।
(बी) पी-ब्लॉक तत्व
समूह 13 से 18 तक के तत्व पी-ब्लॉक का निर्माण करते हैं। सामान्य इलेक्ट्रॉनिक विन्यास [अक्रिय गैस] है$ns^{2}np^{1-6}$
(सी) डी-ब्लॉक तत्व
समूह 3 से 12 तत्व डी-ब्लॉक का निर्माण करते हैं। सामान्य इलेक्ट्रॉनिक विन्यास [अक्रिय गैस] है $(n-1) d^{1-10} n s^{1-2}$
(डी) एफ-ब्लॉक तत्व
सामान्य इलेक्ट्रॉनिक विन्यास है $(n-2) f^{1-14}(n-1) d^{0-1} n s^{2}$.
सभी एफ-ब्लॉक तत्व संबंधित हैं $3^{rd} $ समूह।
एफ-ब्लॉक के तत्वों को दो श्रृंखलाओं में वर्गीकृत किया गया है।
(1) $1^{st}$ आंतरिक संक्रमण या 4 एफ-श्रृंखला में 14 तत्व होते हैं ${}_{58} Ce$
को ${}_{71} Le$.
(2) $2^{nd}$ आंतरिक संक्रमण या 5 एफ-श्रृंखला में 14 तत्व होते हैं ${}_{90} Th$
को ${}_{103} Lr$.
अवधि, समूह और ब्लॉक की भविष्यवाणी:
-
किसी तत्व की अवधि संयोजकता कोश की प्रमुख क्वांटम संख्या से मेल खाती है।
-
किसी तत्व का ब्लॉक उपकोश के प्रकार से मेल खाता है जो अंतिम इलेक्ट्रॉन प्राप्त करता है।
-
समूह की भविष्यवाणी संयोजकता कोश या/और अंतिम कोश में इलेक्ट्रॉनों की संख्या से निम्नानुसार की जाती है।
$\quad $(ए) एस-ब्लॉक तत्वों के लिए; $\quad $ समूह संख्या = संख्या वैलेंस इलेक्ट्रॉनों का
$\quad $(बी) पी-ब्लॉक तत्वों के लिए; $\quad $ ग्रुप नं. =10+ नहीं. वैलेंस इलेक्ट्रॉनों का
$\quad $(सी) डी-ब्लॉक तत्वों के लिए; $\quad $ ग्रुप नं. = नहीं. में इलेक्ट्रॉनों की $(n-1)$ उपकोश + सं. संयोजकता कोश में इलेक्ट्रॉनों की.
धातु और अधातु:
-
धातुओं की विशेषता यह है कि वे आसानी से इलेक्ट्रॉन छोड़ देते हैं और चमक कम कर देते हैं। धातुओं का समावेश अधिक होता है $78 %$ सभी ज्ञात तत्व और आवर्त सारणी के बाईं ओर दिखाई देते हैं। धातुएँ आमतौर पर कमरे के तापमान (पारा, गैलियम को छोड़कर) पर ठोस होती हैं। इनका गलनांक और क्वथनांक उच्च होता है और ये ऊष्मा और बिजली के अच्छे संवाहक होते हैं। धातुओं के ऑक्साइड आमतौर पर प्रकृति में क्षारीय होते हैं (कुछ धातुएँ अपनी उच्च ऑक्सीकरण अवस्था में अम्ल ऑक्साइड बनाती हैं जैसे$CrO_{3}$
-
अधातुएँ इलेक्ट्रॉन नहीं खोती हैं बल्कि इलेक्ट्रॉन ग्रहण करके संगत ऋणायन बनाती हैं। अधातुएँ आवर्त सारणी के शीर्ष दाईं ओर स्थित हैं। अधातुएँ आमतौर पर कमरे के तापमान पर कम पिघलने और क्वथनांक वाले ठोस, तरल या गैस होते हैं। ये ऊष्मा और विद्युत के कुचालक होते हैं। अधातुओं के ऑक्साइड सामान्यतः अम्लीय प्रकृति के होते हैं।
धातु (अर्धधातु) :
मेटलॉइड्स में बी, सी, जीई, एएस, एसबी और टी तत्व शामिल हैं।
विकर्ण संबंध:
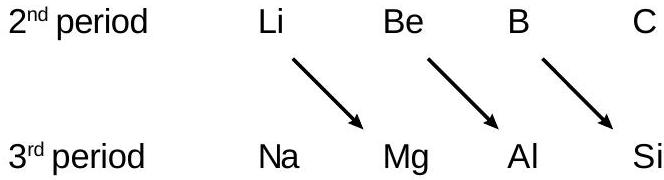
विकर्ण संबंध उत्पन्न होता है;
(i) किसी समूह में नीचे उतरने पर परमाणुओं और आयनों का आकार बढ़ जाता है। आवर्त सारणी में बाएँ से दाएँ जाने पर आकार घटता जाता है।
इस प्रकार तिरछे घूमने पर आकार लगभग समान रहता है। (ली= 1.23$A^{o}$ एवं एमजी= 1.36$A^{o}$ ; $Li^{+}$= 0.76$A^{o}$ & $Mg^{2+}$= 0.72$A^{o}$ )
(ii) कभी-कभी यह सुझाव दिया जाता है कि विकर्ण संबंध इलेक्ट्रोनगेटिविटी मूल्यों में विकर्ण समानता के कारण उत्पन्न होता है।
(Li= 1.0 और Mg= 1.36 ; Be= 1.5 और Al= 1.5 ; B= 2.0 और Si= 1.8)
परमाणु गुणों की आवधिकता:
(i) प्रभावी परमाणु चार्ज:
प्रभावी परमाणु प्रभार $\left(Z_{\text {eff }}\right)=Z-\sigma$, (कहाँ $Z$ वास्तविक परमाणु आवेश (तत्व का परमाणु क्रमांक) है और $\sigma$ परिरक्षण (स्क्रीनिंग) स्थिरांक है)। का मान है $\sigma$ यानी स्लेटर के नियमों का उपयोग करके परिरक्षण प्रभाव निर्धारित किया जा सकता है।
(ii) परमाणु त्रिज्या:
(ए) सहसंयोजक त्रिज्या:
यह एक सहसंयोजक बंधन द्वारा बंधे दो नाभिकों (समान परमाणुओं के) के केंद्रों के बीच की दूरी का आधा है। सहसंयोजक त्रिज्या का प्रयोग आमतौर पर अधातुओं के लिए किया जाता है।
(बी) वेंडर वाल त्रिज्या (टकराव त्रिज्या):
यह ठोस अवस्था में पदार्थ के दो निकटतम पड़ोसी अणुओं में दो आसन्न परमाणुओं के बीच आंतरिक परमाणु दूरी का आधा है।
(सी) धात्विक त्रिज्या (क्रिस्टल त्रिज्या):
यह धात्विक क्रिस्टल जाली में दो आसन्न धातु परमाणुओं के नाभिक के बीच की दूरी का आधा है।
- इस प्रकार, सहसंयोजक, वेंडर दीवार और धात्विक त्रिज्या परिमाण के अनुसार क्रम का पालन करते हैं,
$$ r_{\पाठ {सहसंयोजक }} $$
(iii) लोनिक त्रिज्या:
आयन के नाभिक के केंद्र से वह प्रभावी दूरी जहां तक उसका आयनिक बंधन में प्रभाव होता है, आयनिक त्रिज्या कहलाती है।
(iv) आयनीकरण ऊर्जा:
लोनिज़ेशन एनर्जी (आईई) को धनायन बनाने के लिए एक पृथक गैसीय परमाणु से सबसे शिथिल बंधे इलेक्ट्रॉन को हटाने के लिए आवश्यक ऊर्जा की मात्रा के रूप में परिभाषित किया गया है।
$M(g) \xrightarrow {\text{IE1}} \mathrm{M}^{+} $ + $e^{-1}$ ;
$M^{+}$(जी)+ $IE_{2}$ $\rightarrow$ $M^{2+}$(जी)+ $e^{-}$
$\mathrm{M}^{2+}(\mathrm{g})+\mathrm{IE}_{3} \longrightarrow \mathrm{M}^{+3}(\mathrm{~g})+\mathrm{e}^{-}$
$IE_1$ , $IE_2$ और $IE_3$ हैं $1^{st}$ , $2^{nd}$ और $3^{rd}$ एक तटस्थ परमाणु मोनोवैलेंट और द्विसंयोजक धनायन से इलेक्ट्रॉन को हटाने के लिए क्रमशः आयनीकरण ऊर्जा। सामान्य रूप में
$ (IE_1) \lt (IE_2) \lt (IE_3) \lt $ ……
एकाकी ऊर्जा को प्रभावित करने वाले कारक
(ए) परमाणु का आकार:
परमाणु आकार में वृद्धि के साथ आयनीकरण ऊर्जा घटती है।
(बी) परमाणु प्रभार:
परमाणु आवेश में वृद्धि के साथ आयनीकरण ऊर्जा बढ़ती है।
(सी) परिरक्षण या स्क्रीनिंग प्रभाव:
आंतरिक कोश में इलेक्ट्रॉनों की संख्या जितनी अधिक होगी, स्क्रीनिंग प्रभाव उतना अधिक होगा और आकर्षण बल कम होगा और इस प्रकार आयनीकरण ऊर्जा (IE) कम हो जाएगी।
(डी) इलेक्ट्रॉन का प्रवेश प्रभाव:
इलेक्ट्रॉनों का प्रवेश प्रभाव क्रम का पालन करता है $s>p>d>f$ के लिए, समान ऊर्जा स्तर। इलेक्ट्रॉन का प्रवेश जितना अधिक होगा, आयनीकरण ऊर्जा उतनी ही अधिक होगी।
(ई) इलेक्ट्रॉनिक कॉन्फ़िगरेशन:
यदि किसी परमाणु में बिल्कुल आधे भरे या पूरी तरह से भरे हुए कक्ष हैं, तो ऐसी व्यवस्था में अतिरिक्त स्थिरता होती है।
(V) इलेक्ट्रॉन गेन एन्थैल्फी: (विषय का नाम बदला गया)
इलेक्ट्रॉन लाभ एन्थैल्पी $\Delta_{\mathrm{eg}} \mathrm{H}^{\Theta}$, मानक दाढ़ एन्थैल्पी में परिवर्तन है जब एक तटस्थ गैसीय परमाणु आयन बनाने के लिए एक इलेक्ट्रॉन प्राप्त करता है।
$$ मैथ्रम $$
दूसरा इलेक्ट्रॉन लाभ एन्थैल्पी, प्रारंभिक तटस्थ परमाणु में एक दूसरे इलेक्ट्रॉन को जोड़ने के लिए एन्थैल्पी परिवर्तन, हमेशा सकारात्मक होता है क्योंकि इलेक्ट्रॉन का प्रतिकर्षण परमाणु आकर्षण को प्रभावित करता है।
-
समूह 17 के तत्वों (हैलोजन) में बहुत अधिक नकारात्मक इलेक्ट्रॉन लाभ एन्थैल्पी (यानी उच्च इलेक्ट्रॉन बंधुता) होती है क्योंकि वे एक इलेक्ट्रॉन उठाकर स्थिर उत्कृष्ट गैस इलेक्ट्रॉनिक विन्यास प्राप्त कर सकते हैं।
-
एक आवर्त में, परमाणु संख्या में वृद्धि के साथ, इलेक्ट्रॉन लाभ एन्थैल्पी अधिक नकारात्मक हो जाती है
-
जैसे-जैसे हम एक समूह में ऊपर से नीचे की ओर बढ़ते हैं, इलेक्ट्रॉन लाभ एन्थैल्पी कम नकारात्मक हो जाती है
-
उत्कृष्ट गैसों में बड़ी धनात्मक इलेक्ट्रॉन लब्धि एन्थैल्पी होती है
-
O या F की ऋणात्मक इलेक्ट्रॉन लब्धि एन्थैल्पी S या Cl से कम है।
-
क्षारीय मृदा धातुओं की इलेक्ट्रॉन लब्धि एन्थैल्पी बहुत कम या धनात्मक होती है
-
नाइट्रोजन में इलेक्ट्रॉन बन्धुता बहुत कम होती है
-
(i) इलेक्ट्रॉन बन्धुता $\propto \frac{1}{\text { Atomic size }}$
-
(ii) इलेक्ट्रॉन बन्धुता $\propto$ प्रभावी नाभिकीय चार्ज $\left(\mathrm{z}_{\mathrm{eff}}\right)$
-
(iii) इलेक्ट्रॉन बन्धुता $\propto \frac{1}{\text { Screening effect }}$.
-
(iv) किसी उपकोश के आधे भरे और पूरी तरह से भरे हुए कक्षकों की स्थिरता तुलनात्मक रूप से अधिक होती है और ऐसे सिस्टम में एक अतिरिक्त इलेक्ट्रॉन जोड़ना मुश्किल होता है और इसलिए इलेक्ट्रॉन बंधुता मूल्य कम हो जाता है।
(VI) इलेक्ट्रोनगेटिविटी:
इलेक्ट्रोनगेटिविटी किसी तत्व की सहसंयोजक बंधित अणुओं में साझा इलेक्ट्रॉनों को अपनी ओर आकर्षित करने की प्रवृत्ति का माप है।
(ए) पॉलिंग का पैमाना:
$ E_{A-B}$ = आबंध एन्थैल्पी/आबंध ऊर्जा $A - B$ गहरा संबंध
$E_{A-A}=$ की बंधन ऊर्जा $A-A$ गहरा संबंध
$E_{B-B}=$ की बंधन ऊर्जा $B-B$ गहरा संबंध
(सभी बंधन ऊर्जाएं अंदर हैं $\mathrm{kcal} / \mathrm{mol}$z )
सभी बंधन ऊर्जाएं अंदर हैं $\mathrm{kJ} / \mathrm{mol}$.
(बी) मुल्लिकेन का पैमाना:
$$ \chi_{M}=\frac{I E+EA}{2} $$
पॉलिंग्स की विद्युत ऋणात्मकता $\chi_{\mathrm{P}}$ मुल्लिकेन की इलेक्ट्रोनगेटिविटी से संबंधित है $\chi_{\mathrm{M}}$ जैसा कि नीचे दिया गया है.
$$ \chi_{P}=1.35\left(\chi_{M}\right)^{1 / 2}-1.37 $$
मुल्लिकेन के मूल्य पॉलिंग के मूल्यों से लगभग 2.8 गुना बड़े थे।
(VII) संयोजकता या ऑक्सीकरण अवस्थाओं की आवधिकता:
ऐसे कई तत्व हैं जो परिवर्तनशील संयोजकता प्रदर्शित करते हैं। यह विशेष रूप से संक्रमण तत्वों और एक्टिनोइड्स की विशेषता है।
(आठवीं) आवधिक रुझान और रासायनिक प्रतिक्रिया:
-
किसी समूह में ऑक्साइड की क्षारीय प्रकृति बढ़ जाती है या अम्लीय प्रकृति कम हो जाती है। धातुओं के ऑक्साइड सामान्यतः क्षारीय होते हैं और अधातुओं के ऑक्साइड अम्लीय होते हैं। मेटलॉइड्स के ऑक्साइड आमतौर पर उभयचर प्रकृति के होते हैं। Be, Al, Zn, Sn, As, Pb, और Sb के ऑक्साइड उभयधर्मी हैं।
-
किसी आवर्त में ऑक्साइड की प्रकृति क्षारीय से अम्लीय तक भिन्न होती है।