सामान्य जैविक रसायन
सामान्य कार्बनिक रसायन विज्ञान में याद रखने योग्य बातें
1.प्रेरक प्रभाव
साधारण $\mathrm{C}-\mathrm{C}$ बंधन में कोई ध्रुवता नहीं होती क्योंकि समान इलेक्ट्रोनगेटिविटी (EN) मान के दो परमाणु एक दूसरे से जुड़े होते हैं। इसलिए बंधन अध्रुवीय है।
यहां अधिक के कारण 1-क्लोरो ब्यूटेन में कार्बन श्रृंखला पर विचार करें $\mathrm{EN}$ का $\mathrm{Cl}$ एटम $\mathrm{C}-\mathrm{Cl}$ आबंध युग्म की ओर थोड़ा विस्थापित है $\mathrm{Cl}$ इसलिए परमाणु आंशिक नकारात्मक बनाता है $(\delta-)$ शुल्क समाप्त हो गया $\mathrm{Cl}$ परमाणु और आंशिक सकारात्मक $\left(\delta^{+}\right)$शुल्क समाप्त हो गया $\mathrm{C}_{1}$ परमाणु.
अब से $C_{1}$ थोड़ा सकारात्मक है, इससे स्थानांतरण भी होगा $C_{1}-C_{2}$ बंधन युग्म इलेक्ट्रॉनों को स्वयं की ओर उत्पन्न करता है $C_{2}$ छोटा धनात्मक आवेश प्राप्त करने के लिए। उसी प्रकार $\mathrm{C}_{3}$ कार्बन श्रृंखला में चार्ज का प्रेरण बनाते हुए थोड़ा सकारात्मक चार्ज प्राप्त करता है। ऐसे प्रभाव को आगमनात्मक प्रभाव कहा जाता है।
I प्रभाव दर्शाने वाला आरेख
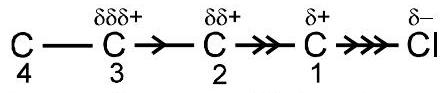
तीर इलेक्ट्रॉन निकालने की प्रकृति को दर्शाता है $-\mathrm{Cl}$ समूह।
इस प्रकार आगमनात्मक प्रभाव को स्थायी विस्थापन के रूप में परिभाषित किया जा सकता है $\sigma$ द्विध्रुव के कारण बंध युग्म इलेक्ट्रॉन। (ध्रुवीय बंधन)
कुछ महत्वपूर्ण बिंदु इस प्रकार हैं:
(ए) इसे आसन्न बंधन के ध्रुवीकरण के कारण एक बंधन के ध्रुवीकरण के रूप में भी परिभाषित किया जा सकता है।
(बी) इसे संचरण प्रभाव भी कहा जाता है।
(सी) यह अणु में स्थायी ध्रुवीकरण का कारण बनता है, इसलिए यह एक स्थायी प्रभाव है।
(डी) सहसंयोजक बंधन में शामिल दो परमाणुओं की इलेक्ट्रोनगेटिविटी में अंतर के कारण इलेक्ट्रॉनों का विस्थापन होता है।
(ई) इलेक्ट्रॉन अपने मूल परमाणु कक्ष को कभी नहीं छोड़ते हैं।
(f) दूरी के साथ इसका परिमाण घटता जाता है और तीसरे कार्बन परमाणु के बाद यह लगभग नगण्य हो जाता है।
(छ) आगमनात्मक प्रभाव सदैव क्रियाशील रहता है $\sigma$ बंधन, शामिल नहीं है $\pi$ बंधन इलेक्ट्रॉन.
आगमनात्मक प्रभावों के प्रकार:
(ए)- I प्रभाव: जो समूह इलेक्ट्रॉन बादल को वापस लेता है उसे - I समूह के रूप में जाना जाता है और इसके प्रभाव को - I प्रभाव कहा जाता है। विभिन्न समूहों को उनके घटते-बढ़ते क्रम में इस प्रकार सूचीबद्ध किया गया है।
$\oplus \quad\quad\quad\quad \oplus \quad\quad\quad\quad \oplus$
$-NR_3 > -SR_2 > -NH_3 > -NO_2 > -SO_{2}R > -CN > -CHO > -COOH > -F > -Cl > -Br > -I > -OR > -OH > -C = CH > -NH_2 > - C_6H_5 > -CH = CH_2 > -H$.
(बी) + I प्रभाव: वह समूह जो इलेक्ट्रॉन बादल छोड़ता है उसे + I समूह और प्रभाव के रूप में जाना जाता है $+\mathrm{I}$ प्रभाव।
$-O^{\ominus} > -COO^{\ominus} > -C(CH_3)_3 > -CH(CH_3)_2 > -CH_2-CH_3 > -CH_3 >-D > -H $
हाइड्रोजन परमाणु का संदर्भ है $+I$ और $-I$ शृंखला। हाइड्रोजन का आगमनात्मक प्रभाव शून्य माना जाता है।
पूर्व। आइये इसके प्रभाव पर विचार करें $COOH$ & $-COO^{-}$कार्बन श्रृंखला में
(ए) ${ }^{\ominus} OOC \rightarrow \stackrel{\delta-}CH_2 \rightarrow \stackrel{\delta \delta-}CH_2 \rightarrow CH_3$
(बी) $HOOC \rightarrow \stackrel{\delta+}CH_2 \rightarrow \stackrel{\delta \delta+}CH_3 $
इस कारण $\mathrm{e}^{-}$दान देने का स्वभाव $-\mathrm{COO}^{\ominus}$ कार्बन शृंखला आंशिक रूप से ऋणात्मक हो गयी है लेकिन $-\mathrm{COOH}$ है - I समूह इसलिए कार्बन श्रृंखला आंशिक रूप से सकारात्मक हो गई है।
2.प्रतिध्वनि
अनुनाद वह घटना है जिसमें परमाणु की समान स्थिति में शामिल दो या दो से अधिक संरचनाओं को एक विशेष प्रजाति के लिए लिखा जा सकता है, उन सभी संभावित संरचनाओं को अनुनाद संरचनाओं या विहित संरचनाओं के रूप में जाना जाता है। प्रतिध्वनि संरचनाएँ केवल काल्पनिक होती हैं लेकिन वे सभी एक वास्तविक संरचना में योगदान करती हैं जिसे अनुनाद संकर कहा जाता है। अनुनाद संकर किसी भी प्रतिध्वनि संरचना की तुलना में अधिक स्थिर है।
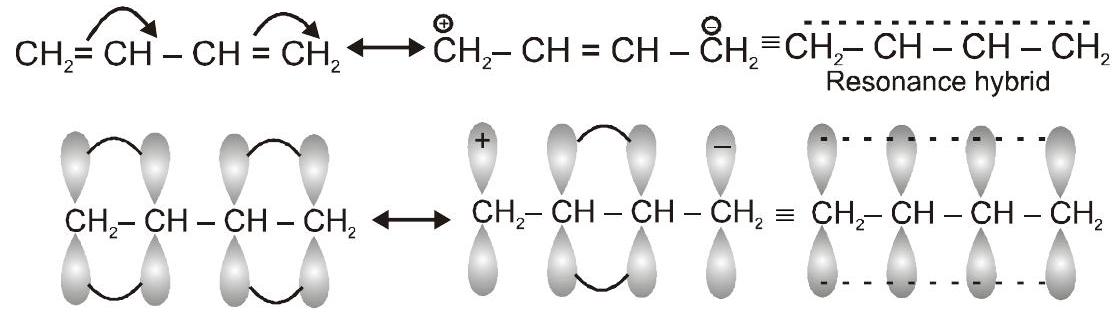
अनुनाद संकर:
सबसे स्थिर प्रतिध्वनि संरचना अनुनाद संकर में अधिकतम योगदान देती है और कम स्थिर प्रतिध्वनि संरचना अनुनाद संकर में न्यूनतम योगदान देती है।
संयुग्मन:
किसी दिए गए परमाणु या समूह को असंतृप्त प्रणाली के साथ संयुग्मित कहा जाता है यदि:-
(i) यह एकल बंधन के माध्यम से एकाधिक बंधन के परमाणुओं में से एक से सीधे जुड़ा हुआ है।
(ii) यह है $\pi$ बंधन, धनात्मक आवेश, ऋणात्मक आवेश, विषम इलेक्ट्रॉन या एकाकी युग्म इलेक्ट्रॉन।
संयुग्मन के प्रकार:
1.के बीच संयुग्मन $\mathrm{C}=\mathrm{C}$ और

- +ve चार्ज और के बीच संयुग्मन

3.अकेले जोड़े और के बीच संयुग्मन

4.विषम इलेक्ट्रॉन और के बीच संयुग्मन
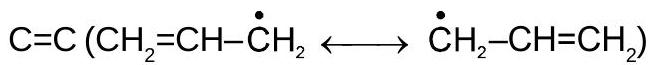
5.नकारात्मक आवेश और के बीच संयुग्मन

3.मेसोमेरिक प्रभाव (या अनुनाद प्रभाव)
मेसोमेरिक प्रभाव को स्थायी प्रभाव के रूप में परिभाषित किया गया है $\pi$ इलेक्ट्रॉन का एकाधिक आबंध से परमाणु में या एकाधिक आबंध से एकल आबंध में या एकाकी युग्म से एकल आबंध में स्थानांतरण। यह प्रभाव मुख्य रूप से दोहरे बंधन की संयुग्मित प्रणाली में काम करता है। अतः इस प्रभाव को संयुग्म प्रभाव भी कहा जाता है।
पूर्व।
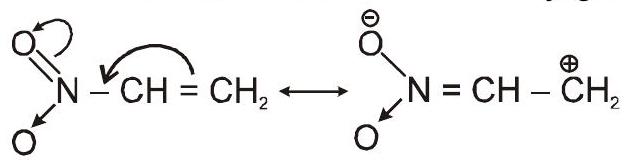
मेसोमेरिक प्रभावों के प्रकार:
(ए) सकारात्मक मेसोमेरिक प्रभाव ( $+M$ प्रभाव) :
जब समूह संयुग्मित प्रणाली को इलेक्ट्रॉन दान करता है तो यह दिखता है $+M$ प्रभाव।
का सापेक्ष क्रम $+\mathrm{M}$ समूह (आमतौर पर अनुसरण किया जाता है):
$-\stackrel{\ominus}O>-NH_{2}>-NHR>-NR_{2}>-OH>-OR>-NHCO>-OCOR>-Ph>-F>-Cl>-Br>-I>-NO$
उदा.(आई)
(बी) नकारात्मक मेसोमेरिक प्रभाव ( $-M$ प्रभाव) :
जब समूह संयुग्मित प्रणाली से इलेक्ट्रॉन निकालता है, तो यह दिखाता है
$-M$ प्रभाव
-M समूहों का सापेक्ष क्रम (आमतौर पर अनुसरण किया जाता है):
पूर्व। (मैं)
(द्वितीय)
4.अतिसंयुग्मन
यह पी-ऑर्बिटल के साथ सिग्मा इलेक्ट्रॉन का डेलोकलाइजेशन है। के रूप में भी जाना जाता है $\sigma \pi$ संयुग्मन या कोई बंधन प्रतिध्वनि नहीं। यह एल्कीन, एल्काइन, कार्बोकेशन, फ्री रेडिकल, बेंजीन न्यूक्लियस में हो सकता है।
आवश्यक शर्त : संतृप्त कार्बन पर कम से कम एक हाइड्रोजन की उपस्थिति $\alpha$ एल्कीन, एल्काइन, कार्बोकेशन, फ्री रेडिकल, बेंजीन न्यूक्लियस के संबंध में।
(i) एल्केन में हाइपरकोन्जुगेशन
(ii) कार्बोकेशन में हाइपरकोन्जुगेशन
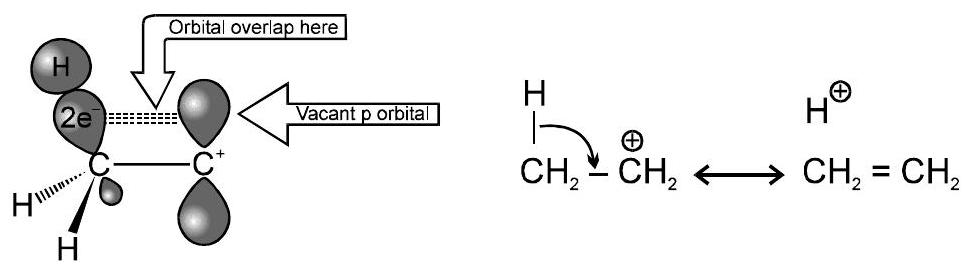
(iii) रेडिकल में हाइपरकोन्जुगेशन
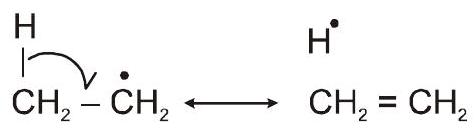
5.सुगंधित चरित्र [द हकेल $4 n+2$ नियम]
निम्नलिखित नियम यह अनुमान लगाने में उपयोगी हैं कि कोई विशेष यौगिक सुगंधित है या गैर-सुगंधित है। सुगंधित यौगिक चक्रीय और समतलीय होते हैं। एक सुगंधित वलय में प्रत्येक परमाणु है $\mathrm{sp}^{2}$ संकरित। चक्रीय $\pi$ आणविक कक्षक (पी-कक्षकों के ओवरलैप द्वारा निर्मित) अवश्य शामिल होना चाहिए $(4 n+2) \pi$ इलेक्ट्रॉन, यानी,$ 2,6,10,14 \ldots \ldots . . \pi $इलेक्ट्रॉन. कहाँ $\mathrm{n}=$ पूर्णांक $0,1,2,3$,
सुगंधित यौगिकों में विशिष्ट गंध होती है, उनमें अतिरिक्त स्थिरता होती है और वे कालिख की लौ के साथ जलते हैं।
ऐरोमैटिक, ऐंटी ऐरोमैटिक और नॉन ऐरोमैटिक यौगिकों के बीच तुलना।
यौगिकों की स्थिरता: सुगंधित > गैर-सुगंधित > प्रति-सुगंधित
(ए) कार्बोकेशन:
परिभाषा: एक कार्बन मध्यवर्ती जिसमें तीन बंध युग्म होते हैं और उस पर एक धनात्मक आवेश होता है, कार्बोकेशन कहलाता है।
संकरण : कार्बोकेशन हो सकता है $sp^2$ & $sp$ संकरित
संकरण $\quad \quad \quad \quad \quad $ उदाहरण
$sp^2$ $ \quad \quad \quad \quad \quad $ $\stackrel \oplus{C}H_{3}, CH_3 \stackrel \oplus{C}H_{2}, CH_3 \stackrel \oplus{C}HCH_{3}, (CH_3)_3 \stackrel\oplus{C}$
$sp$ $ \quad \quad \quad \quad \quad $ $\mathrm{H}_{2} \mathrm{C}=\stackrel{\oplus}{\mathrm{C}} \mathrm{H}, \mathrm{HC} \equiv \stackrel{\oplus}{\ गणित{सी}} $
कार्बोकेशन में इलेक्ट्रॉन की कमी होती है। उनके संयोजकता कोश में केवल छह इलेक्ट्रॉन होते हैं, और इस वजह से, कार्बोकेशन लुईस एसिड के रूप में कार्य करते हैं। अधिकांश कार्बोधनायन अल्पकालिक और अत्यधिक प्रतिक्रियाशील होते हैं, वे मध्यवर्ती के रूप में होते हैं कुछ कार्बनिक प्रतिक्रियाओं में. कार्बोकेशन लुईस बेस या आयनों के साथ प्रतिक्रिया करते हैं जो इलेक्ट्रॉन जोड़ी दान कर सकते हैं, उन्हें इलेक्ट्रॉनों का एक स्थिर ऑक्टेट प्राप्त करने की आवश्यकता होती है (यानी, एक उत्कृष्ट गैस का इलेक्ट्रॉनिक विन्यास):
चूँकि कार्बोकेशन इलेक्ट्रॉन चाहने वाले अभिकर्मक हैं, रसायनज्ञ उन्हें इलेक्ट्रोफाइल कहते हैं। प्रोटॉन सहित सभी लुईस एसिड इलेक्ट्रोफाइल हैं। एक इलेक्ट्रॉन युग्म को स्वीकार करके, एक प्रोटॉन हीलियम के संयोजकता कोश विन्यास को प्राप्त करता है; कार्बोकेशन नियॉन के वैलेंस शेल कॉन्फ़िगरेशन को प्राप्त करते हैं।
स्थिरता : कार्बोकेशन किसके द्वारा स्थिर होते हैं
(i) + I प्रभाव
(ii) $+M$ प्रभाव
(iii) अतिसंयुग्मन
(iv) आवेश का स्थानीयकरण
सामान्य स्थिरता क्रम:
(बी) कार्बोनियन:
परिभाषा: एक कार्बन मध्यवर्ती जिसमें तीन बंध युग्म और उस पर एक ऋणात्मक आवेश होता है, कार्बोनियन कहलाता है।
संकरण : कार्बोनियन का संकरण हो सकता है $sp^3, sp^2$ & $sp$.
संकरण $ \quad \quad \quad \quad \quad $ उदाहरण
कार्बनियन की स्थिरता: कार्बनियन को इलेक्ट्रॉन निष्कासन प्रभाव द्वारा स्थिर किया जाता है
(i) - मैं प्रभाव डालता हूँ
(ii) $-\mathrm{m}$ प्रभाव
(iii) आवेश का स्थानीयकरण
(सी) फ्री रेडिकल्स:
सहसंयोजक बंधन के होमोलिसिस के परिणामस्वरूप मुक्त मूलक मध्यवर्ती में अयुग्मित इलेक्ट्रॉन होते हैं।
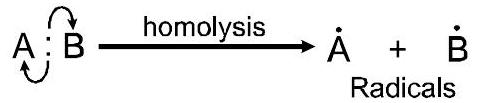
यह सूर्य के प्रकाश, पेरोक्साइड या उच्च तापमान की उपस्थिति में उत्पन्न होता है
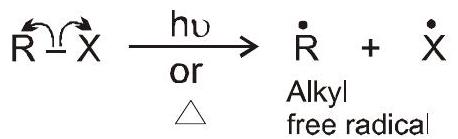
मुक्त रेडिकल: एक अनावेशित मध्यवर्ती जिसमें कार्बन पर तीन बंध युग्म और एक अयुग्मित इलेक्ट्रॉन होता है।
(i) यह विषम के साथ तटस्थ प्रजाति है $\mathrm{e}^{-}$
(ii) विषम होने के कारण यह अनुचुंबकीय प्रकृति का है $\mathrm{e}^{-}$
(iii) आम तौर पर कोई पुनर्व्यवस्था नहीं देखी जाती है।
(iv) विषम इलेक्ट्रॉन वाले कार्बन परमाणु में है $\mathrm{sp}^{2}$ संकर अवस्था
(v) कोई भी प्रतिक्रिया यदि सूर्य के प्रकाश, पेरोक्साइड या उच्च तापमान की उपस्थिति में की जाती है तो यह आम तौर पर मुक्त मूलक मध्यवर्ती के माध्यम से आगे बढ़ती है।
मुक्त रेडिकल की स्थिरता: यह अनुनाद, हाइपरकोन्जुगेशन और + I समूहों द्वारा स्थिर होती है।
पूर्व। $(H_3C)_{3}C^{\bullet}>H_3 C-\dot{C} H-CH_3>H_3 C-\dot{C} H_2>\dot{C} H_3$
(स्थिरता क्रम)
(डी) कार्बेन (डाइवलेंट कार्बन मध्यवर्ती):
परिभाषा : मध्यवर्तीयों का एक समूह है जिसमें कार्बन केवल दो आबंध बनाता है। इन तटस्थ द्विसंयोजक कार्बन प्रजातियों को कार्बेन कहा जाता है। अधिकांश कार्बेन अत्यधिक अस्थिर होते हैं जो केवल क्षणभंगुर अस्तित्व में ही सक्षम होते हैं। कार्बेन बनने के तुरंत बाद, वे आमतौर पर अन्य अणुओं के साथ प्रतिक्रिया करते हैं। कार्बाइन तैयार करने की विधियाँ:

(ई) नाइट्रेन्स:
कार्बेन का नाइट्रोजन एनालॉग नाइट्रेन है। वे बहुत अधिक प्रतिक्रियाशील होते हैं क्योंकि उनमें अष्टक होता है $\mathrm{N}$ अधूरा है. नाइट्रेन में केवल एक संयोजकता होती है $\mathrm{N}$ संतुष्ट हैं।
$$ \mathrm{R}-\ddot{\mathrm{N}} \quad \quad \quad \mathrm{H}-\ddot{\mathrm{N}} $$
(एफ) बेंज़ीन:
बेंजीन रिंग में एक अतिरिक्त है $\mathrm{C}-\mathrm{C} \pi$ बेंजीन में बंधन
स्पष्ट रूप से, हम देख सकते हैं कि नवगठित $\pi$ बंधन दूसरे के साथ प्रतिध्वनि में प्रवेश नहीं कर सकता $\pi$ वलय की कक्षाएँ। चूँकि यह लम्बवत् तल में है।
यह भी ध्यान रखना महत्वपूर्ण है कि ‘बेन्ज़िनिक बॉन्ड’ में शामिल प्रत्येक कार्बन का संकरण होता है $\mathrm{sp}^{2}$ चूँकि इनके बीच ओवरलैप है $\mathrm{sp}^{2}$ हाइब्रिड ऑर्बिटल्स इतना प्रभावी नहीं है।





