रासायनिक प्रतिक्रिया की दर/वेग:

दर $=\frac{\Delta \mathrm{c}}{\Delta \mathrm{t}}=\frac{\mathrm{mol} / \text { lit. }}{\mathrm{sec}}=\mathrm{mol} \quad \mathrm{lit}^{-1}$ समय $^{-1}=\mathrm{mol} \quad \mathrm{dm}^{-3}$ समय $^{-1}$

रासायनिक प्रतिक्रिया की दरों के प्रकार:

एक प्रतिक्रिया के लिए $\mathrm{R} \longrightarrow \mathrm{P}$

सामान्य दर $=\frac{\text { Total } \text { change in concentration }}{\text { Total time taken }}$

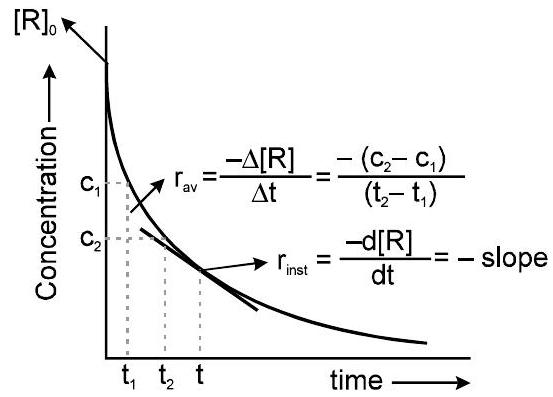
$\mathrm{R}_{\text {instantaneous }}=\lim _{\mathrm{t} \rightarrow 0}\left[\frac{\Delta \mathrm{c}}{\Delta \mathrm{t}}\right]=\frac{\mathrm{dc}}{\mathrm{dt}}=-\frac{\mathrm{d}[\mathrm{R}]}{\mathrm{dt}}=\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{dt}}$

दर कानून (अभिकारकों की सांद्रता पर दर की निर्भरता):

दर $=K$ (संक्षिप्त) $^{\text {order }}$ - अंतर दर समीकरण या दर अभिव्यक्ति

कहाँ $\mathrm{K}=$ दर स्थिरांक = विशिष्ट प्रतिक्रिया दर $=$ प्रतिक्रिया की दर जब एकाग्रता एकता है

की इकाई $\mathrm{K}=(\text { conc })^{1-\text { order }}$ समय $^{-1}$

प्रतिक्रिया का क्रम:

$m_{1}A + m_{2}B \longrightarrow$ उत्पाद.

$R \propto[A]^{P}[B]^{q} \quad$ कहाँ $p$ के बराबर हो भी सकता है और नहीं भी $m_{1}$ और इसी तरह $q$ के बराबर हो भी सकता है और नहीं भी $m_{2}$.

$p$ अभिकारक के संबंध में प्रतिक्रिया का क्रम है $A$ और $q$ अभिकारक के संबंध में प्रतिक्रिया का क्रम है $B$ और $(p+q)$ प्रतिक्रिया का समग्र क्रम है.

एकीकृत दर कानून:

$C_0 \text{ or ‘a’ is initial concentration and } C_1 \text{ or a }- \text { x is concentration at time} ’t’$

(ए) शून्य क्रम प्रतिक्रियाएं:

$\quad\quad$ दर $=\mathrm{k}[\text { conc. }]^{\circ}=$ स्थिर

$\quad\quad$ दर $= k = \frac{C_0 - C_1}{’t’}\quad or \quad C_1= C_0-kt$

$\quad\quad$ की इकाई $K=\mathrm{mol} \quad \mathrm{lit}^{-1} \mathrm{sec}^{-1}$, पूरा होने का समय $=\frac{\mathrm{C}_{0}}{\mathrm{k}}$

$\quad\quad$ पर $t_{1 / 2}, C_{t}=\frac{C_{0}}{2}, \quad so \quad kt_{1 / 2}=\frac{C_{0}}{2}$

$\quad\quad$ $\rightarrow t_{1 / 2}=\frac{C_{0}}{2k} \quad \therefore t_{1 / 2} \propto C_{0}$

(बी) प्रथम क्रम प्रतिक्रियाएं:

$\quad\quad$(i) चलो ए $1^{\text {st }}$ आदेश प्रतिक्रिया है, $A \longrightarrow$ उत्पादों

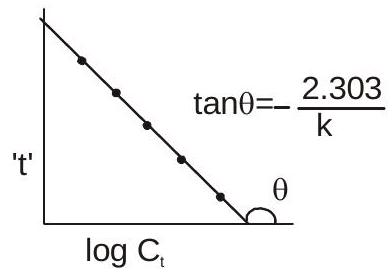
$\quad\quad$$t=\frac{2.303}{k} \log \frac{a}{ax} \quad$ or $\quad k=\frac{2.303}{t} \log \frac{C_{0}}{C_{t}}$

$\quad\quad$$\दायाँ तीर \quad \mathrm{t}_{1 / 2}=\frac{\ell \mathrm{n} 2}{\mathbf{k}}=\frac{0.693}{\mathbf{k}}=$ प्रारंभिक एकाग्रता से स्वतंत्र.

$\quad\quad$$t_{औसत.} = \frac{1}{k} = 1.44\quad t_{1/2}.$

सचित्र प्रदर्शन :

$t=-\frac{2.303}{k} \log C_{t}+\frac{2.303}{k} \log C_{0}$

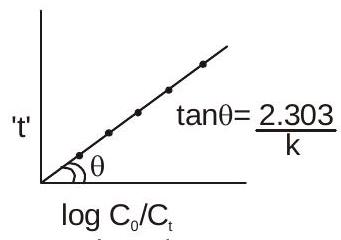
या $\log a / a-x$

(सी) दूसरे क्रम की प्रतिक्रिया:

$\quad\quad$$2^{\text {nd }}$ ऑर्डर प्रतिक्रियाएं

$\quad\quad$ दो प्रकार

$\quad\quad$ $A+A \longrightarrow \text { products }$

$\quad\quad$ $a \quad a $

$\quad\quad$ $(a-x)(a-x) $

$\quad\quad$ $\therefore \frac{d x}{d t}=k(a-x)^{2} $

$\quad\quad$ $\Rightarrow \frac{1}{(a-x)}-\frac{1}{a}=k t $

$\quad\quad$ $A+B \longrightarrow \text { products. }$

$\quad\quad$ $ a \quad b $

$\quad\quad$ $a-x \quad b-x $

$\quad\quad$ $\frac{d x}{d t}=k(a-x)(b-x)$

$\quad\quad$ $ k=\frac{2.303}{t(a-b)} \log \frac{b(a-x)}{a(b-x)}$

प्रतिक्रिया का क्रम निर्धारित करने की विधियाँ

(ए) प्रारंभिक दर विधि:

$$ r=k[A]^{\mathrm{a}}[\mathrm{B}]^{\mathrm{b}}[\mathrm{C}]^{\mathrm{c}} \quad \text { यदि } \quad[\mathrm{B}]=\text { स्थिरांक } $$

$$ \quad \quad\quad\quad\quad\quad\quad\quad\quad\quad [C]=\text { स्थिरांक } $$

तो हमारे पास A की दो भिन्न आरंभिक सांद्रताएँ हैं

$r_{0_{1}} = k[A_0]_1^{a},$

$r_{0_{2}} = k[A_0]_2^{a}$

$\implies \frac{r_{0_1}}{r_{0_2}} = \big(\frac{[A_0]_1}{[A_0]_2}\big)^a$

(बी) एकीकृत दर कानून का उपयोग करना:

यह परीक्षण और त्रुटि की विधि है.

(सी) आधे जीवन की विधि:

के लिए $\mathrm{n}^{\text {th }}$ आदेश प्रतिक्रिया $\quad t_{1 / 2} \propto \frac{1}{\left[R_{0}\right]^{n-1}}$

(डी) ओस्टवाल्ड अलगाव विधि:

दर $=k[A]^{a}[B]^{b}[C]^{c}=k_{0}[A]^{a}$

प्रतिक्रिया की प्रगति की निगरानी करने के तरीके:

(ए) गैसीय प्रतिक्रिया की प्रगति की निगरानी एक निश्चित मात्रा & तापमान पर कुल दबाव को मापकर या स्थिर दबाव और तापमान के तहत मिश्रण की कुल मात्रा को मापकर की जा सकती है।

$\therefore \quad k = \frac{2.303}{t} log\frac{P_0(n-1)}{nP_0-P_t}$

{फॉर्मूला कब लागू नहीं होता $\mathrm{n}=1$, का मान है $\mathrm{n}$ भिन्नात्मक भी हो सकता है.}

(बी) अनुमापन विधि द्वारा:

1. $\quad \therefore a \propto V_{0} \quad a-x \propto V_{t}$

$\Rightarrow k=\frac{2.303}{t} \log \frac{V_{0}}{V_{t}}$

2. ईस्टर के एसिड हाइड्रोलिसिस का अध्ययन।

$k= \frac{2.303}{t}log\frac{V_{\infty-V_0}}{V_{\infty-V_t}}$

(सी) प्रतिक्रिया मिश्रण द्वारा उत्पादित ऑप्टिकल रोटेशन को मापकर:

$k=\frac{2.303}{\mathrm{t}} \log \left(\frac{\theta_{0}-\theta_{\infty}}{\theta_{\mathrm{t}}-\theta_{\infty}}\right)$

प्रतिक्रिया की दर पर तापमान का प्रभाव

टीसी $=\frac{K_{t+10}}{K_t} \approx 2$ से 3 (अधिकांश प्रतिक्रियाओं के लिए)

प्रतिक्रिया दर का अरहेनियस सिद्धांत

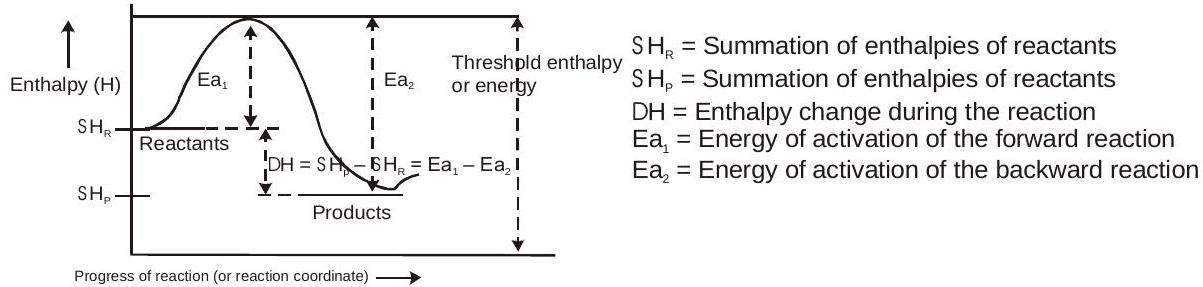
$E_P > E_r \rightarrow$ एन्दोठेर्मिक

$E_P < E_r \rightarrow$ एक्ज़ोथिर्मिक

$\Delta H=\left(E_{p}-E_{r}\right)=$ एन्थैल्पी परिवर्तन

$\Delta H=E_{af}-E_{ab}$

$E_{threshold} = E_{af} + E_r = E_b + E_p$

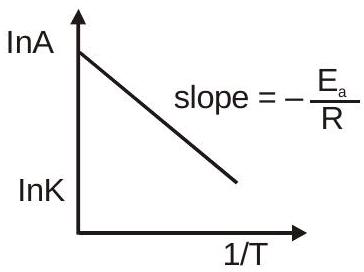
अरहेनियस समीकरण

$ k = A_e^{-E_{a}RT} \quad r=k[conc.]^{order}$

$\frac{d ln k}{dT}=\frac{E_a}{RT^{2}}$

$\log k=(-\frac{Ea}{2.303 R}) \frac{1}T+\log A$

अगर $k_1 \quad and \quad k_2$ दो अलग-अलग तापमानों पर एक प्रतिक्रिया की दर स्थिरांक हो $T_1 \quad and \quad T_2$ क्रमशः, तो हमारे पास है

$$ \log \frac{k_{2}}{k_{1}}=\frac{E_{a}}{2.303 R} \cdot\left(\frac{1}{T_{1}}-\frac{1 }{T_{2}}\दाएं) $$

एलएनके = एलएन $A-\frac{E_a}{RT}$

$\mathrm{E}_{\mathrm{a}} \geq \mathrm{O}$

$\mathrm{T} \rightarrow \infty, \mathrm{K} \rightarrow \mathrm{A}.$