रासायनिक बंध :

इस प्रक्रिया में प्रत्येक परमाणु अक्रिय गैसों का एक स्थिर बाहरी इलेक्ट्रॉनिक विन्यास प्राप्त कर लेता है।

आयनिक या इलेक्ट्रोवैलेंट बॉन्ड:

आयनिक यौगिक का निर्माण मुख्य रूप से इस पर निर्भर करता है:

• संबंधित तटस्थ परमाणुओं से सकारात्मक और नकारात्मक आयनों के निर्माण में आसानी।
• ठोस में धनात्मक एवं ऋणात्मक आयनों की व्यवस्था अर्थात क्रिस्टलीय यौगिक की जाली।

आयनिक यौगिकों के निर्माण की शर्तें

(i) दो संयोजित तत्वों के बीच विद्युत ऋणात्मकता का अंतर बड़ा होना चाहिए।

(ii) आयनीकरण एन्थैल्पी $\left(\mathrm{M}(\mathrm{g}) \rightarrow \mathrm{M}^{+}(\mathrm{g})+\mathrm{e}^{-}\right)$विद्युत धनात्मक तत्व का मान कम होना चाहिए।

(iii) इलेक्ट्रॉन लब्धि एन्थैल्पी का ऋणात्मक मान $\left(\mathrm{X}(\mathrm{g})+\mathrm{e}^{-} \rightarrow \mathrm{X}^{-}(\mathrm{g}))\right.$ विद्युत ऋणात्मक तत्व की मात्रा अधिक होनी चाहिए।

(iv) जालक एन्थैल्पी $\left(\mathrm{M}^{+}(\mathrm{g})+\mathrm{X}^{-}(\mathrm{g}) \rightarrow \mathrm{MX}(\mathrm{s})\right)$ किसी आयनिक ठोस की मात्रा अधिक होनी चाहिए।

जाली एन्थैल्पी:

एक आयनिक ठोस की जाली एन्थैल्पी को एक ठोस आयनिक यौगिक के एक मोल को गैसीय घटक आयनों में पूरी तरह से अलग करने के लिए आवश्यक ऊर्जा के रूप में परिभाषित किया गया है।

आयनिक यौगिक की जालक ऊर्जा को प्रभावित करने वाले कारक

(i) जालक ऊर्जा $\propto \frac{1}{r_{+}+r_{-}}$कहाँ $\left(r_{+}+r_{-}\right)=$अंतर-आयनिक दूरी.

(ii) जालक ऊर्जा $\propto Z_{+}, Z_{-}$

$\mathrm{Z}_{+} \Rightarrow$ इलेक्ट्रॉनिक चार्ज के संदर्भ में धनायन पर चार्ज।

$\mathrm{Z}_{-} \Rightarrow$ ऋणायन पर इलेक्ट्रॉनिक आवेश के रूप में आवेश।

जालक ऊर्जा का निर्धारण:

बॉर्न-हैबर साइकिल:

यह आयनिक यौगिक के निर्माण के दौरान शामिल विभिन्न ऊर्जा शर्तों से संबंधित है।

यह हेस के निरंतर ताप योग के नियम पर आधारित एक थर्मोकेमिकल चक्र है।

हाइड्रेशन:

सभी सरल लवण पानी में घुल जाते हैं, जिससे आयन उत्पन्न होते हैं, और परिणामस्वरूप घोल बिजली का संचालन करता है। तब से $\mathrm{Li}^{+}$यह बहुत छोटा है, यह अत्यधिक हाइड्रेटेड है। इससे रेडियस हाइड्रेटेड हो जाता है $\mathrm{Li}^{+}$आयन बड़ा है और इसलिए यह धीरे-धीरे चलता है। इसके विपरीत, $\mathrm{Cs}^{+}$अपने बड़े आकार और इस प्रकार की त्रिज्या के कारण सबसे कम हाइड्रेटेड है $\mathrm{Cs}^{+}$आयन हाइड्रेटेड की त्रिज्या से छोटा है $\mathrm{Li}^{+}$, और इसलिए हाइड्रेटेड $\mathrm{Cs}^{+}$तेजी से चलता है, और अधिक तत्परता से बिजली का संचालन करता है।

हाइड्रोलिसिस:

हाइड्रोलिसिस का अर्थ है पानी के अणुओं के साथ प्रतिक्रिया जो अंततः टूटने की ओर ले जाती है $\mathrm{O}-\mathrm{H}$ में बंधन $\mathrm{H}^{+}$और $\mathrm{OH}^{-}$आयन।

सहसंयोजक यौगिकों में हाइड्रोलिसिस आम तौर पर दो तंत्रों द्वारा होता है

(ए) समन्वय बंधन निर्माण द्वारा: आम तौर पर परमाणुओं के हैलाइडों में रिक्त स्थान होता है $\mathrm{d}$- रिक्त कक्षकों वाले परमाणुओं के कक्षक या हैलाइड।

(बी) एच-बंध निर्माण द्वारा: उदाहरण के लिए नाइट्रोजन ट्राइहैलाइड्स में

आयनिक संघटक के सामान्य गुण क्या है :

(ए) भौतिक स्थिति:

कमरे के तापमान पर आयनिक यौगिक या तो ठोस अवस्था में या घोल अवस्था में मौजूद होते हैं लेकिन गैसीय अवस्था में नहीं।

(बी) सरल आयनिक यौगिक समावयवता नहीं दर्शाते हैं लेकिन समरूपता उनका महत्वपूर्ण लक्षण है। उदाहरण- $FeSO_{4} .7H_{2}O \quad $ | $\quad MgSO_{4}$.$7H_{2}O$

(सी) विद्युत चालकता:

सभी आयनिक ठोस पिघली हुई अवस्था के साथ-साथ अपने जलीय घोल में भी अच्छे चालक होते हैं क्योंकि उनके आयन गति करने के लिए स्वतंत्र होते हैं।

(डी) आयनिक यौगिकों की घुलनशीलता:

पानी जैसे ध्रुवीय विलायकों में घुलनशील जिनमें उच्च ढांकता हुआ स्थिरांक होता है

आयनिक यौगिकों में सहसंयोजक लक्षण (फ़जन का नियम)

फैजन ने बताया कि किसी अणु में ऋणायन का ध्रुवीकरण जितना अधिक होता है, उसमें सहसंयोजक गुण उतना ही अधिक होता है।

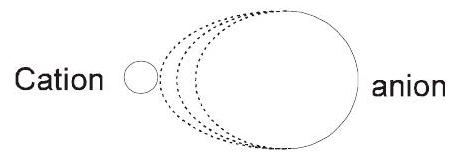
ऋणायन का विरूपण जितना अधिक होगा ध्रुवीकरण उतना ही अधिक होगा सहसंयोजक गुण बढ़ जायेगा।

फैजान ने कुछ नियम दिए हैं जो आयनिक यौगिकों में सहसंयोजक चरित्र को नियंत्रित करते हैं, जो इस प्रकार हैं

(i) धनायन का आकार: धनायन का आकार $\alpha 1$ / ध्रुवीकरण।

(ii) ऋणायन का आकार : ऋणायन का आकार $\alpha$ ध्रुवीकरण

(iii) धनायन पर शुल्क : धनायन पर शुल्क $\alpha$ ध्रुवीकरण।

(iv) ऋणायन पर आवेश: ऋणायन पर आवेश $\alpha$ ध्रुवीकरण।

(v) धनायन का छद्म अक्रिय गैस विन्यास :

सहसंयोजक बंधन :

यह अणुओं को बनाने के लिए परमाणुओं के बीच वैलेंस इलेक्ट्रॉनों को साझा करने से बनता है, उदाहरण के लिए, का निर्माण $\mathrm{Cl}_{2}$ अणु :

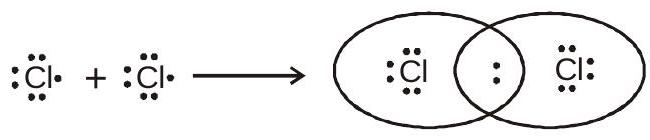
$$ \text { या } \mathrm{Cl}-{\mathrm{Cl}} $$

दो के बीच सहसंयोजक बंधन $\mathrm{Cl}$ परमाणुओं

महत्वपूर्ण शर्तें यह हैं कि:

(i) प्रत्येक बंधन परमाणुओं के बीच एक इलेक्ट्रॉन जोड़ी के बंटवारे के परिणामस्वरूप बनता है।

(ii) प्रत्येक संयोजन परमाणु साझा जोड़ी में कम से कम एक इलेक्ट्रॉन का योगदान देता है।

(iii) संयोजित परमाणु इलेक्ट्रॉनों के आदान-प्रदान के परिणामस्वरूप बाहरी कोश उत्कृष्ट गैस विन्यास प्राप्त करते हैं।

समन्वय बांड (डेटिव बांड):

दो परमाणुओं के बीच बनने वाला बंधन जिसमें इलेक्ट्रॉन युग्म का योगदान उनमें से एक द्वारा किया जाता है जबकि साझाकरण दोनों द्वारा किया जाता है।

(मैं) $\mathrm{NH}_{4}^{+}$(अमोनियम आयन)

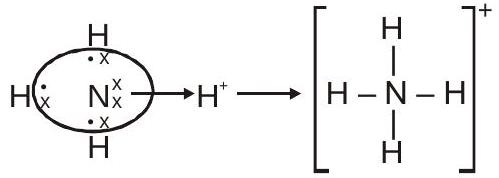
दाता $\rightarrow$ हुंडी सकारनेवाला

(ii) $\mathrm{O}_{3}$ (ओजोन)

अन्य उदाहरण: $H_{2}SO_{4}$, $HNO_{3}$, $H^{3}O^{+}$, $N_{2}O$, [$Cu(NH_{3})_4]^{2+}$

औपचारिक आरोप :

औपचारिक शुल्क किसी दी गई प्रजाति के लिए कई संभावित लुईस संरचनाओं में से सबसे कम ऊर्जा संरचना के चयन में मदद करते हैं।

ऑक्टेट नियम की सीमाएँ:

1. केंद्रीय परमाणु का अधूरा अष्टक

LiCl, $BeH_{2}$,और $BCl_{3}$, $AlCl_{3}$,और $BF_{3}$.

2. विषम-इलेक्ट्रॉन अणु

नाइट्रिक ऑक्साइड, $\mathrm{NO}$ और नाइट्रोजन डाइऑक्साइड. $\mathrm{NO}_{2}$

$$ \ddot{N}=\ddot{O} \quad \ddot{O}=\dot{N}^{+}-\ddot{O}: $$

3. विस्तारित ऑक्टेट

4. अष्टक सिद्धांत की अन्य कमियाँ :

(i) कुछ उत्कृष्ट गैसें (उदाहरण के लिए क्सीनन और क्रिप्टन) भी ऑक्सीजन और फ्लोरीन के साथ मिलकर कई यौगिक बनाती हैं जैसे $XeF_{2}$, $KrF_{2}$, $XeOF_{2}$ वगैरह।,

(ii) यह सिद्धांत अणुओं के आकार का वर्णन नहीं करता है।

(iii) यह किसी अणु की ऊर्जा के बारे में पूरी तरह से मौन होने के कारण अणुओं की सापेक्ष स्थिरता की व्याख्या नहीं करता है।

वैलेंस बांड सिद्धांत (वीबीटी):

$H_{2}$(जी) + 435.8 केजे$mol^{-}$ $\rightarrow$ एच(जी) + एच(जी)

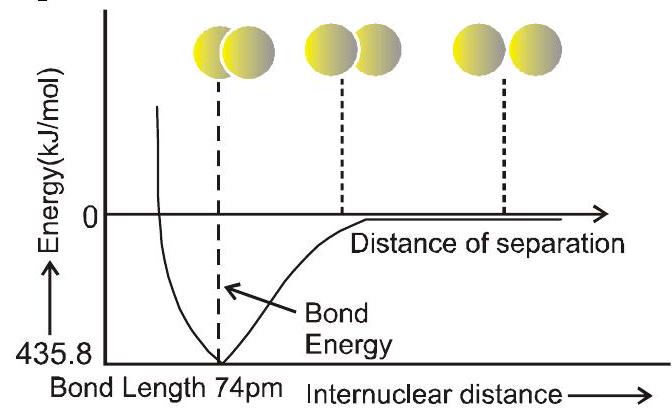
कक्षीय ओवरलैप अवधारणा:

कक्षीय ओवरलैप अवधारणा के अनुसार, दो परमाणुओं के बीच सहसंयोजक बंधन का निर्माण विपरीत स्पिन वाले वैलेंस शेल में मौजूद इलेक्ट्रॉनों की जोड़ी के परिणामस्वरूप होता है।

ओवरलैपिंग के प्रकार और सहसंयोजक बंधों की प्रकृति

ओवरलैपिंग के प्रकार के आधार पर सहसंयोजक बंधन को दो प्रकारों में वर्गीकृत किया जा सकता है:

(i) सिग्मा( $\sigma$ ) गहरा संबंध

(ii) पाई $(\pi)$ गहरा संबंध

(i) सिग्मा $(\sigma)$ बंधन: इस प्रकार का सहसंयोजक बंधन आंतरिक परमाणु अक्ष के साथ बंधन कक्षकों के अंत से अंत (हेड-ऑन) ओवरलैप द्वारा बनता है।

• पीपी ओवरलैपिंग : इस प्रकार का ओवरलैप आधे भरे हुए के बीच होता है $p$-आने वाले दो परमाणुओं की कक्षाएँ।

(ii) $\quad \mathrm{pi}(\pi)$ बंधन : के निर्माण में $\pi$ परमाणु कक्षकों को इस तरह ओवरलैप करते हुए बांधें कि उनकी अक्षें एक-दूसरे के समानांतर और आंतरिक अक्ष के लंबवत रहें।

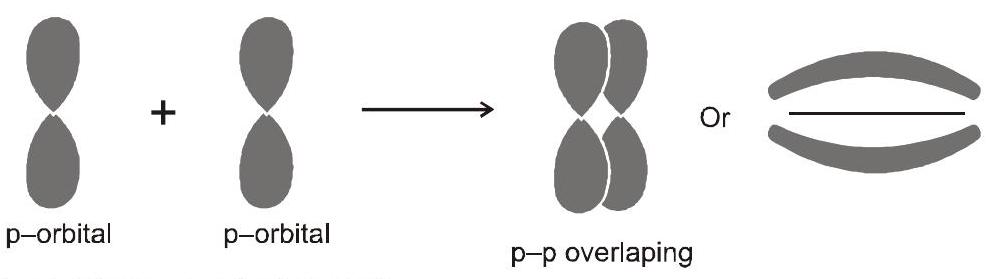
सिग्मा और पाई बांड की ताकत:

सिग्मा बंधन के मामले में, ऑर्बिटल्स का ओवरलैपिंग काफी हद तक होता है। इसलिए, यह पाई बॉन्ड की तुलना में अधिक मजबूत है जहां ओवरलैपिंग की सीमा कुछ हद तक होती है।

वैलेंस शेल इलेक्ट्रॉन जोड़ी प्रतिकर्षण (VSEPR) सिद्धांत)

वीएसईपीआर सिद्धांत के मुख्य सिद्धांत इस प्रकार हैं:

(i) एक अणु का आकार केंद्रीय परमाणु के चारों ओर वैलेंस शेल इलेक्ट्रॉन जोड़े [बंधित या गैर-बंधित] की संख्या पर निर्भर करता है।

(ii) संयोजकता कोश में इलेक्ट्रॉनों के जोड़े एक दूसरे को प्रतिकर्षित करते हैं क्योंकि उनके इलेक्ट्रॉन बादल ऋणात्मक रूप से आवेशित होते हैं।

(iii) इलेक्ट्रॉनों के ये जोड़े अंतरिक्ष में ऐसे स्थान पर कब्जा कर लेते हैं जिससे प्रतिकर्षण कम हो जाता है और इस प्रकार उनके बीच की दूरी अधिकतम हो जाती है।

(iv) संयोजकता कोश को एक गोले के रूप में लिया जाता है, जिसमें इलेक्ट्रॉन जोड़े एक दूसरे से अधिकतम दूरी पर गोलाकार सतह पर स्थित होते हैं।

(v) एक मल्टीपल बॉन्ड को इस तरह माना जाता है जैसे कि यह एक एकल इलेक्ट्रॉन जोड़ी है और मल्टीपल बॉन्ड के दो या तीन इलेक्ट्रॉन जोड़े को एक सिंगल सुपर पेयर के रूप में माना जाता है।

(vi) जहां दो या दो से अधिक अनुनाद संरचनाएं एक अणु का प्रतिनिधित्व कर सकती हैं, वीएसईपीआर मॉडल ऐसी किसी भी संरचना पर लागू होता है।

इलेक्ट्रॉन युग्मों की प्रतिकारक अंतःक्रिया इस क्रम में घटती है:

अयुग्मित युग्म $(\ell \mathrm{p})$ - अयुग्मित युग्म $(\ell \mathrm{p})>$ अयुग्मित युग्म $(\ell \mathrm{p})$ - बंधन जोड़ी $(\mathrm{bp})>$ बांड जोड़ी (बीपी) - बांड जोड़ी

संकरण:

संकरण की मुख्य विशेषताएं:

1. संकर कक्षकों की संख्या संकरित होने वाले परमाणु कक्षकों की संख्या के बराबर होती है।

2. संकरित कक्षाएँ हमेशा ऊर्जा और आकार में समतुल्य होती हैं।

3. शुद्ध परमाणु ऑर्बिटल्स की तुलना में हाइब्रिड ऑर्बिटल्स स्थिर बंधन बनाने में अधिक प्रभावी होते हैं।

4. इन हाइब्रिड ऑर्बिटल्स को अंतरिक्ष में कुछ पसंदीदा दिशा में निर्देशित किया जाता है ताकि इलेक्ट्रॉन जोड़े के बीच न्यूनतम प्रतिकर्षण हो और इस प्रकार एक स्थिर व्यवस्था प्राप्त हो। इसलिए, संकरण का प्रकार अणुओं की ज्यामिति को इंगित करता है।

संकरण के लिए महत्वपूर्ण शर्तें:

(i) परमाणु के संयोजकता कोश में मौजूद कक्षाएँ संकरित होती हैं।

(ii) संकरण से गुजरने वाले कक्षकों में लगभग समान ऊर्जा होनी चाहिए।

(iii) संकरण से पहले इलेक्ट्रॉन का संवर्धन आवश्यक शर्त नहीं है।

(iv) यह कक्षक है जो संकरण से गुजरता है, इलेक्ट्रॉन नहीं।

एक अणु या आयन में एक परमाणु के संकरण का निर्धारण: स्टेरिक संख्या नियम (गिलेस्पी द्वारा दिया गया):

एक परमाणु की स्टेरिक संख्या $=$ उस परमाणु के साथ बंधे परमाणु की संख्या + उस परमाणु पर बचे एकाकी जोड़े की संख्या।

डी-ऑर्बिटल से जुड़ा संकरण:

‘डी’ऑर्बिटल का प्रकार शामिल है।

आणविक कक्षीय सिद्धांत (एमओटी):

1932 में एफ. हंड और आरएस मुल्लिकेन द्वारा विकसित।

(i) आणविक कक्षाएँ तुलनीय ऊर्जा और उचित समरूपता के परमाणु कक्षाओं के संयोजन से बनती हैं।

(ii) परमाणु कक्षक में एक इलेक्ट्रॉन एक नाभिक से प्रभावित होता है, जबकि आणविक कक्षक में यह अणु में परमाणुओं की संख्या के आधार पर दो या दो से अधिक नाभिक से प्रभावित होता है। इस प्रकार एक परमाणु कक्षक एककेन्द्रित होता है जबकि एक आणविक कक्षक बहुकेन्द्रित होता है।

(iii) बनने वाले आणविक कक्षकों की संख्या संयोजित परमाणु कक्षकों की संख्या के बराबर होती है। जब दो परमाणु कक्षक आपस में जुड़ते हैं, तो दो आणविक कक्षक बनते हैं, जिन्हें आबंधन आण्विक कक्षक और प्रतिबंधन आण्विक कक्षक कहा जाता है।

(iv) परमाणु ऑर्बिटल्स की तरह आणविक ऑर्बिटल्स को पॉली एक्सक्लूजन सिद्धांत और हंड्स रूल ऑफ मैक्सिमम मल्टीप्लिसिटी का पालन करते हुए औफबाउ सिद्धांत के अनुसार भरा जाता है। लेकिन इन आणविक कक्षाओं का भरने का क्रम हमेशा प्रयोगात्मक रूप से तय किया जाता है, ऐसा कोई नियम नहीं है $(n+I)$ परमाणु कक्षकों के मामले में नियम।

परमाणु कक्षाओं के संयोजन के लिए शर्तें:

1. संयोजित परमाणु कक्षकों की ऊर्जा समान या लगभग समान होनी चाहिए।

2. संयोजित परमाणु कक्षकों में आणविक अक्ष के बारे में समान समरूपता होनी चाहिए।

3. संयोजित परमाणु कक्षाएँ अधिकतम सीमा तक ओवरलैप होनी चाहिए।

आण्विक कक्षकों के लिए ऊर्जा स्तर आरेख:

विभिन्न आणविक कक्षकों की ऊर्जाओं का बढ़ता क्रम $\mathrm{O}{2}$ और $\mathrm{F}{2}$ नीचे दिया गया है:

$\sigma 1 s<\sigma^{\star} 1 s<\sigma 2 s<\sigma^{\star} 2 s<\sigma 2 p_{z}<\left(\pi 2 p_{x}=\pi 2 p_{y}\right)<\left(\pi^{\star} 2 p_{x}=\pi^{\star} 2 p_{y}\right)<\sigma^{\star} 2 p_{z}$ इस क्रम की महत्वपूर्ण विशेषता यह है कि इसकी ऊर्जा $\sigma 2 p_{z}$ आणविक कक्षक की तुलना में अधिक है $\pi 2 p_{x}$ और $\pi 2 p_{y}$ आणविक कक्षाएँ।

अनुबंध आदेश

बांड ऑर्डर (बीओ) = $\frac{1}{2} $ ($N_{b}$ -$N_{a}$)

एक सकारात्मक बांड आदेश (यानी, $N_{b}>N_{a}$ ) का अर्थ है एक स्थिर अणु जबकि ऋणात्मक (अर्थात्, $N_{b}<N_{a}$ ) या शून्य (यानी, $N_{b}=N_{a}$ ) बंधन क्रम का अर्थ है एक अस्थिर अणु।

बंधपत्र की प्रकृति:

1, 2 या 3 के इंटीग्रल बॉन्ड ऑर्डर मान क्रमशः सिंगल, डबल या ट्रिपल बॉन्ड के अनुरूप होते हैं।

बॉन्ड लंबाई :

एक अणु में दो परमाणुओं के बीच बंधन क्रम को बंधन लंबाई के अनुमानित माप के रूप में लिया जा सकता है। बांड क्रम बढ़ने पर बांड की लंबाई कम हो जाती है।

चुंबकीय प्रकृति:

यदि किसी अणु में सभी आणविक कक्षाएँ दोगुनी व्याप्त हैं, तो पदार्थ प्रतिचुंबकीय (चुंबकीय क्षेत्र द्वारा प्रतिकर्षित) होता है, उदाहरण के लिए, $\mathrm{N}_{2}$ अणु.

द्विध्रुव आघूर्ण :

द्विध्रुव आघूर्ण $(\mu)=$ आवेश का परिमाण $(q) \times$ अलगाव की दूरी $(d)$ द्विध्रुव आघूर्ण आमतौर पर डिबाई इकाइयों (डी) में व्यक्त किया जाता है। रूपांतरण कारक हैं

हे $1 \mathrm{D}=3.33564 \times 10^{-30} \mathrm{Cm}$, कहाँ $\mathrm{C}$ कूलम्ब है और $\mathrm{m}$ मीटर है.

ओ 1 डेबाई $=1 \times 10^{-18}$ ईएसयू सेमी.

उदाहरण के लिए एचएफ के द्विध्रुव आघूर्ण को इस प्रकार दर्शाया जा सकता है

$$ \mathrm{H}-\ddot{\mathrm{F}}: $$

इलेक्ट्रॉन घनत्व में बदलाव को बदलाव की दिशा को इंगित करने के लिए लुईस संरचना के ऊपर क्रॉस किए गए तीर द्वारा दर्शाया गया है। एक अणु में द्विध्रुव आघूर्ण होगा यदि सभी व्यक्तिगत आघूर्ण वेक्टर का योग गैर-शून्य है।

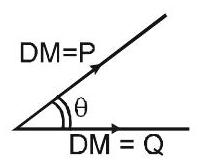
$R=\sqrt{P^{2}+Q^{2}+2 P Q \cos \theta}$,

कहाँ $\mathrm{R}$ परिणामी द्विध्रुव आघूर्ण है।

प्रतिध्वनि:

परिभाषा :

अनुनाद को उस घटना के रूप में परिभाषित किया जा सकता है जिसमें परमाणु की समान स्थिति में शामिल दो या दो से अधिक संरचनाओं को एक विशेष यौगिक के लिए लिखा जा सकता है।

उदाहरण के लिए, ओजोन, $\mathrm{O}_{3}$ अणु को नीचे दर्शाई गई संरचनाओं I और II द्वारा समान रूप से दर्शाया जा सकता है।

में प्रतिध्वनि $\mathrm{O}_{3}$ अणु

रेजोनेंस हाइब्रिड:

यह सभी विभिन्न संभावित संरचनाओं की वास्तविक संरचना है जिसे परमाणुओं के लिए अधिकतम सहसंयोजकता के नियमों का उल्लंघन किए बिना अणु के लिए लिखा जा सकता है।

हाइड्रोजन बंध :

$$ \mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}\mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}\mathrm{H}^ {डेल्टा+}-मैथर्म{एफ}^{डेल्टा-} $$

एच-बॉन्ड के लिए आवश्यक शर्तें

(i) अणु में अधिक विद्युत ऋणात्मक परमाणु होना चाहिए $(F, O, N)$ से जुड़ा हुआ $\mathrm{H}$-परमाणु.

(ii) विद्युत ऋणात्मक परमाणु का आकार छोटा होना चाहिए।

(iii) विद्युत ऋणात्मक परमाणु पर एक अकेला युग्म मौजूद होना चाहिए।

आदेश के $\mathrm{H}$-रिश्ते की ताक़त

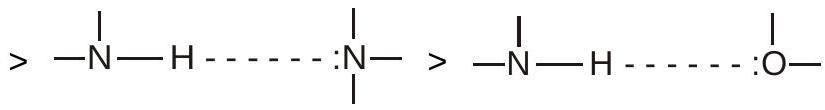
एच-बॉन्ड के प्रकार:

(ए) इंट्रामोल्युलर एच-बॉन्डिंग:

यह तब बनता है जब हाइड्रोजन परमाणु दो अत्यधिक विद्युत ऋणात्मक ( $\mathrm{F}, \mathrm{O}, \mathrm{N})$ एक ही अणु के भीतर परमाणु.

ओ-हाइड्रॉक्सी बेंजाल्डिहाइड

इसके पैरा-व्युत्पन्न की तुलना में इसका क्वथनांक कम (यानी अधिक अस्थिर) होता है

इंट्रामोलेक्यूलर हाइड्रोजन-बॉन्डिंग के निर्माण के लिए आवश्यक शर्तें:

(ए) हाइड्रोजन बंधन के परिणामस्वरूप बनने वाला वलय समतल होना चाहिए।

(बी) 5- या 6-सदस्यीय अंगूठी बनाई जानी चाहिए।

(सी) परस्पर क्रिया करने वाले परमाणुओं को इस तरह से रखा जाना चाहिए कि रिंग बंद होने के दौरान न्यूनतम तनाव हो।

(बी) अंतरआण्विक एच-बॉन्डिंग:

यह एक ही या अलग-अलग यौगिकों के दो अलग-अलग अणुओं के बीच बनता है।

(ए) पानी के अणुओं में

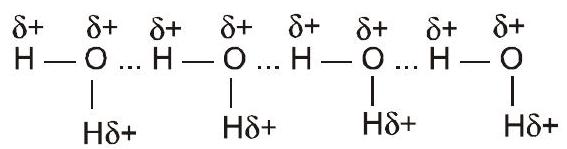
(बी) एचएफ में हाइड्रोजन बांड लिंक करते हैं $\mathrm{F}$ एक अणु के परमाणु के साथ $\mathrm{H}$-दूसरे अणु का परमाणु, इस प्रकार एक ज़िग-ज़ैग श्रृंखला बनाता है $(\mathrm{HF})_{n}$ ठोस में भी और तरल में भी।

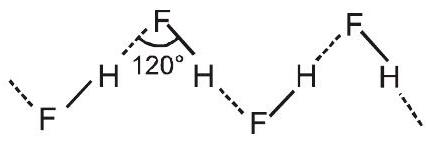
अंतरआण्विक बल (वैंडर वाल्स बल):

अंतरआण्विक आकर्षण दो या दो से अधिक अणुओं को एक साथ बांधे रखता है। ये सबसे कमजोर रासायनिक बल हैं और निम्न प्रकार के हो सकते हैं।

(ए) आयन-द्विध्रुव आकर्षण।

(बी) द्विध्रुव-द्विध्रुव आकर्षण।

(सी) आयन-प्रेरित द्विध्रुवीय आकर्षण।

(डी) द्विध्रुव-प्रेरित द्विध्रुव आकर्षण।

(ई) तात्क्षणिक द्विध्रुव- तात्क्षणिक प्रेरित द्विध्रुव आकर्षण।

(फैलाव बल या लंदन बल)

• वेंडर वाल फोर्स की ताकत $\propto$ मॉलिक्यूलर मास्स।

• वैन डेर वाल का बल $\propto$ क्वथनांक।

धात्विक बंधन :

धात्विक बंधन को समझाने के लिए दो मॉडलों पर विचार किया जाता है:

(ए) इलेक्ट्रॉन-समुद्र मॉडल

(बी) बैंड मॉडल

कुछ विशेष संबंध स्थितियाँ:

(ए) इलेक्ट्रॉन की कमी वाले बंधन: ऐसे कई यौगिक हैं जिनमें सामान्य सहसंयोजक बंधन या समन्वय बंधन के अलावा कुछ इलेक्ट्रॉन की कमी वाले बंधन मौजूद होते हैं। इन इलेक्ट्रॉन की कमी वाले बांडों में अपेक्षा से कम इलेक्ट्रॉनों की संख्या होती है जैसे कि डाइबोरेन में मौजूद तीन केंद्र-दो इलेक्ट्रॉन बांड (3c-2e) $B_{2}H_{6}$, $Al_2 $ $ (CH_3)_6 $, $BeH_2(s)$ और धातु कार्बोनिल्स को पाटना

(बी) बैक बॉन्डिंग: बैक बॉन्डिंग आम तौर पर तब होती है जब दो बंधे परमाणुओं में से एक परमाणु में खाली ऑर्बिटल्स होते हैं (आमतौर पर यह परमाणु दूसरे या तीसरे अवधि से होता है) और दूसरे बंधे हुए परमाणु में कुछ गैर-बंधित होते हैं इलेक्ट्रॉन युग्म (आम तौर पर यह परमाणु दूसरे आवर्त का होता है)। बैक बॉन्डिंग से बॉन्ड की ताकत बढ़ती है और बॉन्ड की लंबाई कम हो जाती है।

उदाहरण के लिए, में $\mathrm{BF}_{3}$

बोरॉन ट्राइहैलाइड्स में बैक बॉन्डिंग की सीमा।

$BF_{3}$> $BCl_{3}$> $BBr_{3}$